Лекция жоспары
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
III бөлім. Жазықтықтағы және кеңістіктегі аналитикалық геометрия 4-тақырып. Жазықтықтағы түзу теңдеулері. Екінші ретті қисықтар Лекция жоспары: Жазықтықтағы координаталар жүйелері. Жазықтықтағы аналитикалық геометрияның қарапайым есептері. Түзудің әртүрлі теңдеулері. Түзудің қалыпты теңдеуі, екінші ретті қисықтар: эллипс, гипербола, парабола және олардың канондық теңдеулері. Декарт координаттарын түрлендіру. Екінші ретті сызықтарды канондық түрге келтірудің ең қарапайым есептері. Шеңбер теңдеуі, Эллипс, гипербола жане парабола теңдеулері Лекцияның қысқаша жазбасы Жазықтықтағы координаталар жүйесі – жазықтықтағы нүктені сандық тұрғыдан суреттеу ұғымын білдіреді. Мұндай жүйелердің бірі тікбұрышты координаталар жүйесі болады. 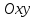 координаталар жүйесіндегі координаталар жүйесіндегі 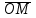 радиус-векторының координаталары М нүктесінің координатасы деп атайды. Егер радиус-векторының координаталары М нүктесінің координатасы деп атайды. Егер 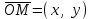 болса, онда М нүктесінің координаталары болса, онда М нүктесінің координаталары 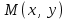 деп жазылады. Мұнда х-саны М нүктесінің абсцисса, ал у-саны М нүктесінің ординатасы болады. деп жазылады. Мұнда х-саны М нүктесінің абсцисса, ал у-саны М нүктесінің ординатасы болады. Бұл екі х және у сандары М нүктесінің жазықтықтағы орналасуын анықтайды. х және у –тің әрбір қос сан сандар мәніне бір ғана М нүктесі сәйкес келеді. Координаталар жүйесінде аса маңызды орын алатын жүйе полярлық координаталар жүйесі. Координаталар жүйесін түрлендіру. Бір координаталар жүйесінен басқа координаталар жүйесіне ауысуын координаталар жүйесін түрлендіру деп атайды. Тікбұрышты координаталар жүйесінің басқа координаталар жүйесіне ауысуын екі жағдайын қарастырайық. Алынған формулалар әр түрлі координаталар жүйесінде жазықтықтан алынған кез-келген нүктенің координаталарының тәуелділігін анықтайды. Координаталар осьтерін параллель көшіру. Жазықтықта 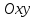 тікбұрышты координаталар жүйесі берілсін. тікбұрышты координаталар жүйесі берілсін. 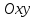 координаталары жүйесінің жаңа координаталары жүйесінің жаңа 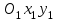 координаталар жүйесіне параллель көшіруде координаталар басы өзгеріп, масштаб бірліктері мен ось бағыттары өзгермейді. координаталар жүйесіне параллель көшіруде координаталар басы өзгеріп, масштаб бірліктері мен ось бағыттары өзгермейді. Жазықтықтағы түзудің теңдеулері. Сызықтардың ішінде ең қарапайымы ол – түзу. Тікбұрышты координаталар жүйесінде Бұрыштың коэффициентпен берілген түзудің теңдеуі Түзу бойынан кез-келген 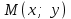 нүктесін аламыз нүктесін аламыз
теңдеуін аламыз, ол кез-келген 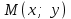 нүктесінің координаталарын қанағаттандырады. нүктесінің координаталарын қанағаттандырады. 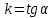 саны түзудің бұрыштық коэффициенті, ал (10.2) теңдеуі – бұрыштық коэффициенті, ал (10.2) теңдеуі бұрыштық коэффициентімен берілген түзудің теңдеуі деп аталады. Түзудің жалпы теңдеуі. саны түзудің бұрыштық коэффициенті, ал (10.2) теңдеуі – бұрыштық коэффициенті, ал (10.2) теңдеуі бұрыштық коэффициентімен берілген түзудің теңдеуі деп аталады. Түзудің жалпы теңдеуі. 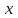 пен пен 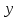 -ке қатысты бірінші дәрежелі түзудің теңдеуін қарастырайық. -ке қатысты бірінші дәрежелі түзудің теңдеуін қарастырайық.
мұндағы 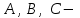 тұрақты шамалар, тұрақты шамалар, 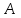 және және 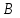 бірдей нөлге тең болмайды. Берілген бағытпен берілген нүктеден өтетін түзудің теңдеуі. бірдей нөлге тең болмайды. Берілген бағытпен берілген нүктеден өтетін түзудің теңдеуі. Түзу 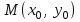 нүктесі арқылы өтетіндіктен, нүктенің координаталары түзудің теңдеуін қанағаттандырады: нүктесі арқылы өтетіндіктен, нүктенің координаталары түзудің теңдеуін қанағаттандырады: 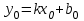 . Бұл теңдеуден . Бұл теңдеуден 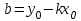 . . 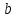 мәнін мәнін 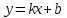 теңдеуіне апарып қойсақ, онда іздеп отырған теңдеуіне апарып қойсақ, онда іздеп отырған 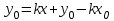 теңдеуін аламыз, яғни теңдеуін аламыз, яғни
Екі нүкте арқылы өтетін түзудің теңдеуі. Түзу 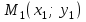 және және 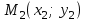 нүктелері арқылы өтеді. нүктелері арқылы өтеді. 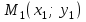 нүктесі арқылы өтетін түзудің теңдеуі нүктесі арқылы өтетін түзудің теңдеуі
мұндағы 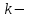 әзірше белгісіз коэффициент. әзірше белгісіз коэффициент. Түзудің нормаль теңдеуі. Түзу р және 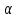 арқылы анықталатын болсын. арқылы анықталатын болсын. 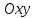 тікбұрышты координаталар жүйесін қарастырайық. Бірақ тікбұрышты және полярлық координаталар жүйесін байланыстыратын тікбұрышты координаталар жүйесін қарастырайық. Бірақ тікбұрышты және полярлық координаталар жүйесін байланыстыратын 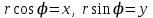 формулалары белгілі. формулалары белгілі.
теңдеуі түзудің нормаль теңдеуі деп аталады. Шеңбер. Екінші ретті қисықтардың ішіндегі ең қарапайым қисық – шеңбер. Радиусы 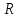 , центрі , центрі 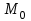 нүктесінде болатын шеңбер деп нүктесінде болатын шеңбер деп 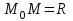 шартын қанағаттандыратын, жазықтықтың барлық шартын қанағаттандыратын, жазықтықтың барлық 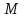 нүктелер жиынын айтатынын еске салайық. Тікбұрышты координаталар жүйесінде нүктелер жиынын айтатынын еске салайық. Тікбұрышты координаталар жүйесінде 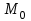 нүктесінің координаталары нүктесінің координаталары 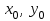 болсын, ал болсын, ал 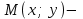 шеңбердің бойынан алынған кез-келген нүкте шеңбердің бойынан алынған кез-келген нүкте 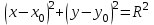 теңдеуі шеңбердің канондық теңдеуі деп аталады. теңдеуі шеңбердің канондық теңдеуі деп аталады. Эллипс. Фокустар деп аталатын берілген екі нүктеден қашықтарының қосындысы әрқашан тұрақты шама болатын нүктелердің геометриялық орындарын эллипс деп аталады 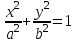 . .Гипербола. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырымы әрқашанда тұрақты шама болатын нүктелерінің геометриялық орындарын гипербола деп аталады 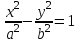 Парабола. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден арақашықтықтары бірдей болатын нүктелердің жиынтығын парабола деп атайды. 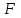 фокусынан директрисаға дейінгі қашықтық параметр деп аталады және фокусынан директрисаға дейінгі қашықтық параметр деп аталады және 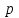 әрпімен белгіленеді. ( әрпімен белгіленеді. (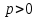 ). ).Параболаның теңдеуін қорытып шығару үшін 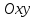 координаталар жүйесін алайық. Ал координаталар басы фокус пен директрисаның дәл ортасына орналастырып, директрисадан координаталар жүйесін алайық. Ал координаталар басы фокус пен директрисаның дәл ортасына орналастырып, директрисадан 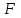 фокусына қарай бағытталған, директрисаға перпендикуляр фокусына қарай бағытталған, директрисаға перпендикуляр 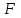 фокусы арқылы өтетін фокусы арқылы өтетін 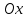 осін алайық. Қарастырып отырған жүйеде осін алайық. Қарастырып отырған жүйеде 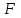 фокусының координаталары фокусының координаталары 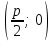 , ал директриса теңдеуі , ал директриса теңдеуі 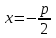 немесе немесе 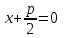 түрінде беріледі. түрінде беріледі. 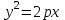 теңдеуі параболаның канондық теңдеуі деп аталады. Парабола екінші ретті сызық болып табылады. теңдеуі параболаның канондық теңдеуі деп аталады. Парабола екінші ретті сызық болып табылады. Ұсынылатын әдебиеттер 1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004. 2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969. 3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004. 4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005. СӨЖ-ге арналған бақылау тапсырмалары ЖҮТ 3.2; [10, том 1, беттер 69-85] Есептер АЗ-3.3; [10, том 1] ЖҮТ 4.1; [10, том 1, беттер 137-142] Есептер АЗ-4.1; [10, том 1] 5-тақырып. Кеңістіктегі жазықтықтың және түзудің теңдеулері. Екінші ретті беттер Лекция жоспары: Кеңістіктегі жазықтық теңдеулері Кеңістіктегі түзу теңдеулері Екінші ретті беттер. Лекцияның қысқаша мазмұны: Кеңістіктегі жазықтық теңдеуі Қарапайым беттердің бір түрі жазықтық. 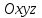 кеңістіктегі жазықтықты әр түрлі түрде беруге болады. Олардың әрқайсысына сәйкес теңдеулері болады. кеңістіктегі жазықтықты әр түрлі түрде беруге болады. Олардың әрқайсысына сәйкес теңдеулері болады.Берілген нүкте арқылы өтетін, берілген векторға перпендикуляр жазықтықтың теңдеуі. 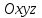 кеңістігінде кеңістігінде 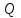 жазықтығы жазықтығы 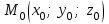 нүктесімен және осы жазықтыққа перпендикуляр нүктесімен және осы жазықтыққа перпендикуляр 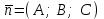 векторымен берілген. векторымен берілген. 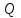 жазықтығының теңдеуін қорытып шығарайық. Жазықтықтан кез-келген жазықтығының теңдеуін қорытып шығарайық. Жазықтықтан кез-келген 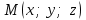 нүктесін алайық және нүктесін алайық және 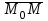 векторын құрайық. векторын құрайық. 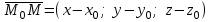 М нүктесі 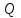 жазықтығында қалай орналассада жазықтығында қалай орналассада 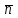 және және 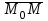 векторлары өзара перпендикуляр болады, сондықтан олардың скаляр көбейтіндісі нөлге тең: векторлары өзара перпендикуляр болады, сондықтан олардың скаляр көбейтіндісі нөлге тең: 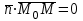 , яғни , яғни
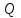 жазықтығының кез-келген нүктесі теңдеуін қанағаттандырады, ал жазықтығының кез-келген нүктесі теңдеуін қанағаттандырады, ал 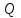 жазықтығында жатпайтын нүктелер қанағаттандырмайды. жазықтығында жатпайтын нүктелер қанағаттандырмайды. 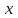 , , 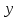 , және , және 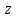 координаталарына байланысты жазықтықтың теңдеуі бірінші дәрежелі болады. координаталарына байланысты жазықтықтың теңдеуі бірінші дәрежелі болады. 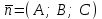 векторы жазықтықтың нормаль векторы деп аталады. Теңдеудегі векторы жазықтықтың нормаль векторы деп аталады. Теңдеудегі 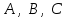 коэффициенттеріне мәндер беріп, коэффициенттеріне мәндер беріп, 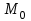 нүктесі арқылы өтетін кез-келген жазықтықтың теңдеуін алуға болады. Берілген нүкте арқылы өтетін жазықтықтар жиынын жазықтықтар байланысы деп, ал (12.3) –жазықтықтар байланысының теңдеуі деп аталады. нүктесі арқылы өтетін кез-келген жазықтықтың теңдеуін алуға болады. Берілген нүкте арқылы өтетін жазықтықтар жиынын жазықтықтар байланысы деп, ал (12.3) –жазықтықтар байланысының теңдеуі деп аталады. Жазықтықтың жалпы теңдеуі 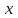 , , 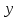 , және , және 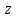 үш белгісізді бірінші дәрежелі теңдеуді қарастырайық: үш белгісізді бірінші дәрежелі теңдеуді қарастырайық:
Осы теңдеуді 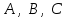 коэффициенттерінің бірдей нөлге тең емес болсын, мысалы, коэффициенттерінің бірдей нөлге тең емес болсын, мысалы, 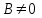 , онда (12.4) теңдеуін былайша жазуға болады: , онда (12.4) теңдеуін былайша жазуға болады:
теңдеуі 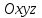 координаталар жүйесіндегі қандай да бір жазықтықты анықтайды. теңдеуі жазықтықтың жалпы теңдеуі деп аталады. координаталар жүйесіндегі қандай да бір жазықтықты анықтайды. теңдеуі жазықтықтың жалпы теңдеуі деп аталады. Берілген үш нүкте арқылы өтетін жазықтықтың теңдеуі Кеңістікте бір түзудің бойында жататын үш нүкте бір ғана жазықтықты анықтайды. Бір түзуде жатпайтын 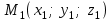 , , 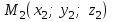 және және 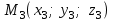 нүктелері арқылы өтетін нүктелері арқылы өтетін 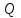 жазықтығының теңдеуін табайық. жазықтығының теңдеуін табайық.Жазықтықтан қалауымызша кез-келген 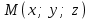 нүктесін алайық және нүктесін алайық және 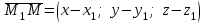 , , 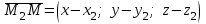 , , 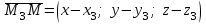 векторларын құрайық. Бұл векторлар векторларын құрайық. Бұл векторлар 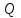 жазықтығында жатады, олар компланарлы векторлар. Векторлардың компланар шартын қолданып (олардың аралас көбейтіндісі нөлге тең), жазықтығында жатады, олар компланарлы векторлар. Векторлардың компланар шартын қолданып (олардың аралас көбейтіндісі нөлге тең), 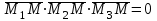 , аламыз, яғни , аламыз, яғни
теңдеуі берілген үш нүкте арқылы өтетін жазықтықтың теңдеуі. Жазықтықтың кесінділер арқылы берілген теңдеуі Жазықтық 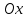 , , 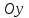 және және 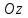 осьтерін осьтерін 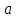 , , 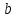 және және 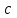 кесінділерін қияды, яғни ол кесінділерін қияды, яғни ол 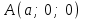 , , 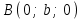 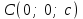 нүктелері арқылы өтеді. нүктелері арқылы өтеді. Осы нүктелердің координаталарын (12.6) теңдеуіне қойып, келесі анықтауышты аламыз
Анықтауышты ашып 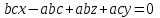 аламыз, яғни аламыз, яғни 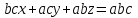 немесе немесе
теңдеуі координаталар осьтеріндегі жазықтық кесінділер бойынша теңдеуі деп аталады. Бұл теңдеу жазықтықтарды салғанда қолданған ыңғайлы. Жазықтықтың нормаль теңдеуі ОК=р болсын, болсын онда 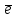 бірлік векторының бірлік векторының 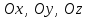 остерімен жасайтын бұрыштары остерімен жасайтын бұрыштары 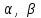 және және 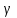 болады. Онда болады. Онда 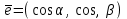 жазықтықпен кез-келген жазықтықпен кез-келген 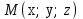 нүктесін алып, оны координаталар басымен қосайық. Сонда нүктесін алып, оны координаталар басымен қосайық. Сонда 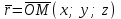 векторын аламыз: векторын аламыз:
(12.8) –теңдеуі векторлық формадағы жазықтықтың нормаль теңдеуі деп аталады. 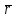 және және 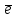 векторларының координаталары белгісіз, векторларының координаталары белгісіз,
теңдеуі координаталық формадағы жазықтықтың нормаль теңдеуі. Кеңістіктегі түзудің теңдеулері. Түзудің векторлық теңдеуі Кеңістіктегі түзудің теңдеуі. Түзудің кез-келген 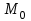 нүктесі және осы нүктесі және осы түзуге параллель 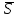 векторымен анықталады. векторымен анықталады. 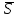 векторы түзудің бағыттауыш векторы деп аталады. векторы түзудің бағыттауыш векторы деп аталады. 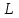 түзуі өзінің түзуі өзінің 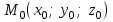 нүктесімен және нүктесімен және 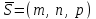 бағыттауыш векторымен берілсін. Түзудің бойынан кез-келген бағыттауыш векторымен берілсін. Түзудің бойынан кез-келген 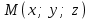 нүктесін белгілеп алайық. нүктесін белгілеп алайық. 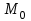 және және 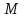 нүктелерінің радиус векторларын нүктелерінің радиус векторларын 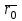 және және 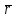 арқылы белгілейік. арқылы белгілейік. 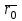 , , 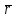 , , 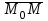 үш векторы үш векторы
қатынасымен байланысты. 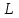 түзуінің бойында жатқан түзуінің бойында жатқан 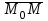 векторы векторы 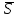 бағыттауыш векторына параллель, сондықтан бағыттауыш векторына параллель, сондықтан 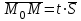 , мұндағы , мұндағы 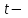 параметр деп аталатын скалярлық көбейткіш, ол түзудің М нүктесінен тәуелді әр түрлі мәндер қабылдайды.формуласын параметр деп аталатын скалярлық көбейткіш, ол түзудің М нүктесінен тәуелді әр түрлі мәндер қабылдайды.формуласын 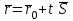 түрінде жазуға болады. Бұл шыққан теңдеуді түзудің векторлық теңдеуі деп аталады. Түзудің параметрлік теңдеуі 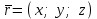 , , 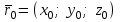 , , 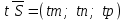 ескере отырып ескере отырып
түрінде жазуға болады. Бұдан
теңдігі шығады. Бұл теңдеуді түзудің параметрлік теңдеуі деп атайды. Түзудің канондық теңдеуі 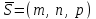 векторы векторы 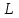 түзуінің бағытауыш векторы, ал түзуінің бағытауыш векторы, ал 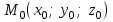 нүктесі осы түзуде жататын нүктесі. нүктесі осы түзуде жататын нүктесі. 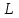 түзуінің бойындағы түзуінің бойындағы 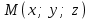 нүктесін нүктесін 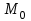 нүктесімен қосып, нүктесімен қосып, 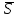 векторына параллель векторына параллель 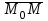 векторын жүргіземіз. Сондықтан, векторын жүргіземіз. Сондықтан, 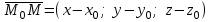 және және 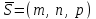 пропорционал болады: пропорционал болады:
теңдеуі түзудің канондық теңдеуі деп аталады. Екі нүкте арқылы өтетін кеңістіктегі түзудің теңдеуі 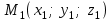 және және 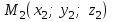 нүктелері арқылы өтетін нүктелері арқылы өтетін 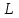 түзуі берілсін. Бағыттауыш түзуі берілсін. Бағыттауыш 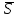 векторы ретінде векторы ретінде 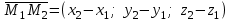 векторын алуға болады, яғни векторын алуға болады, яғни 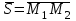 (76-суретті қара). Демек, (76-суретті қара). Демек, 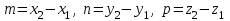 . Түзу . Түзу 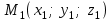 нүктесі арқылы өтетін болғандықтан, (12.13) теңдеуі бойынша, нүктесі арқылы өтетін болғандықтан, (12.13) теңдеуі бойынша, 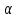 түзуінің теңдеуі келесі түрде болады түзуінің теңдеуі келесі түрде болады
теңдеуі берілген екі нүкте арқылы өтетін түзудің теңдеуі деп аталады. Түзудің жалпы теңдеуі Кеңістіктегі түзудің теңдеуі параллель емес екі жазықтық қиылсықанда пайда болған сызық арқылы беріледі
теңдеулер жүйесін қарастырайық. Бұл жүйенің әрбір теңдеуі жазықтықты анықтайды. Егер жазықтықтар параллель емес болса ( 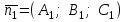 және және 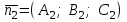 ) векторларының координаталары пропорционал болмайды.) онда координаталары осы жүйенің әрбір теңдеуін қанағаттандыратын, кеңістіктегі геометриялық орны болатын ) векторларының координаталары пропорционал болмайды.) онда координаталары осы жүйенің әрбір теңдеуін қанағаттандыратын, кеңістіктегі геометриялық орны болатын 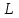 түзуін анықтайды. түзуін анықтайды. Цилиндрлік беттер Тұрақты бағытын сақтай отырып және 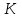 қисығын қиятын қисығын қиятын 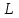 түзуінің бойымен жылжығанда қозғалысынан пайда болған кеңістікте орналасқан бетті цилиндрлік бет немесе цилиндр деп атайды. түзуінің бойымен жылжығанда қозғалысынан пайда болған кеңістікте орналасқан бетті цилиндрлік бет немесе цилиндр деп атайды. 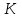 қисығын-цилиндрлік бағыттаушысы, ал қисығын-цилиндрлік бағыттаушысы, ал 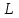 - цилиндрлік жасаушысы деп атайды Бағыттаушысы координаталар жазықтығының біреуінде, ал жасаушылары координаталар осьтерінде параллель және осы жазықтыққа перпедикуляр орналасқан цилиндрлік бетті қарастырайық. - цилиндрлік жасаушысы деп атайды Бағыттаушысы координаталар жазықтығының біреуінде, ал жасаушылары координаталар осьтерінде параллель және осы жазықтыққа перпедикуляр орналасқан цилиндрлік бетті қарастырайық. Теңдеуі 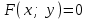 болатын, болатын, 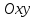 жазықтығында жататын қандай да бір жазықтығында жататын қандай да бір 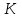 сызығын қарастырайық. Бағыттаушысы сызығын қарастырайық. Бағыттаушысы 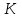 болатын және болатын және 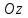 осіне паралллель бағыттауыш бар цилиндрді салайық. осіне паралллель бағыттауыш бар цилиндрді салайық. Айналу беттері. Конустық беттер Егер кеңістікте қандай да бір жазық қисық осьті айналса, оның айналуынан пайда болған бетті айналу беті деп атайды. Қандай да бір 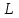 қисығы қисығы 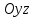 жазықтығында жатсын. Бұл қисықтың теңдеуі жазықтығында жатсын. Бұл қисықтың теңдеуі 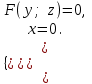 түрінде жазылсын. түрінде жазылсын. Берілген Р нүктесі арқылы өтетін және 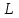 қисық сызығымен қиылсады түзу сызықтармен пайда болған бетті конустық бет немесе конус деп атайды. Мына қисық сызығымен қиылсады түзу сызықтармен пайда болған бетті конустық бет немесе конус деп атайды. Мына 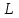 сызығы – конустың бағыттауышысы, ал Р нүктесі – оның төбесі, ал бетті сипаттайтын түзу жасаушысы деп атайды. сызығы – конустың бағыттауышысы, ал Р нүктесі – оның төбесі, ал бетті сипаттайтын түзу жасаушысы деп атайды. 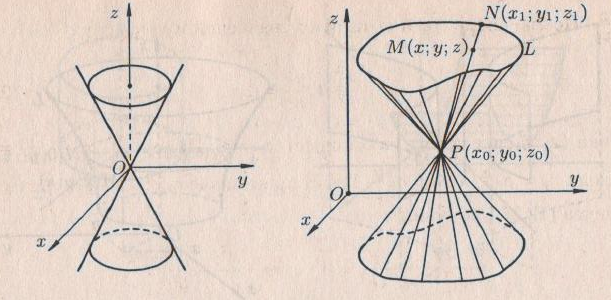 Екінші ретті беттердің конустық теңдеуі Берілген екінші ретті беттердің теңдеуінен оның геометриялық түрін анықталады. Эллипсоид 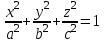 теңдеуімен берілген бетті зерттейміз. Бетінің тұйық, сопақ бет болатындығын көрсетеді. (12.28) беті эллипсоид деп аталады. теңдеуімен берілген бетті зерттейміз. Бетінің тұйық, сопақ бет болатындығын көрсетеді. (12.28) беті эллипсоид деп аталады. 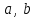 және және 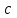 шамалары эллипсоидтың жарты осьтері деп аталады. Егер олар әртүрлі болса, онда эллипсоид үш осьті деп, ал екі жарты осі тең болса, онда үш осьті эллипсоид айналу эллипсоидына айналады, егер шамалары эллипсоидтың жарты осьтері деп аталады. Егер олар әртүрлі болса, онда эллипсоид үш осьті деп, ал екі жарты осі тең болса, онда үш осьті эллипсоид айналу эллипсоидына айналады, егер 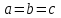 , яғни жарты осьтері өзара тең болса, онда ол сфера , яғни жарты осьтері өзара тең болса, онда ол сфера 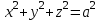 деп аталады. деп аталады. Бір қуысты гиперболоид 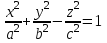 . Бұл қиманың сараптамасы . Бұл қиманың сараптамасы 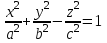 теңдеуі мен анықталатын беттің шексіз формасы кеңейтілген түтікше форма тәрізді екенін көрсетеді. теңдеуі мен анықталатын беттің шексіз формасы кеңейтілген түтікше форма тәрізді екенін көрсетеді. 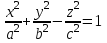 бет бірқуысты гиперболоид деп аталады. бет бірқуысты гиперболоид деп аталады. Ұсынылатын әдебиеттер 1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004. 2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969. 3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004. 4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005. СӨЖ-ге арналған бақылау тапсырмалары ЖҮТ 3.1; [10, том 1, беттер 69-85] Есептер АЗ-3.1; АЗ-3.2; [10, том 1] |

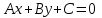 ,
, 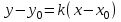 .
. 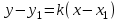 .
. 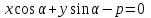 .
. 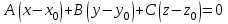 .
.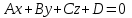 .
.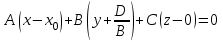 .
.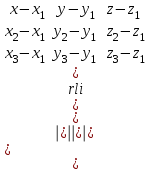 .
.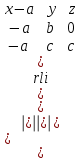 .
.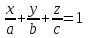 .
.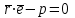 ,
,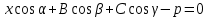 ,
,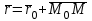 .
.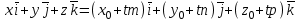 .
.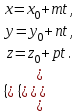
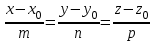 .
.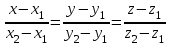 .
.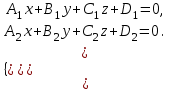 ,
,