Лекция жоспары
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
Жоғарғы математика кафедрасы С. К. Тутанов ZhG 3 Жаратылыстану ғылымдары модулі студенттері үшін «Математика» пәні бойынша ДӘРІСТЕРДІҢ ҚЫСҚАША ЖАЗБАСЫ 2017 І бөлім. Сызықтық алгебра 1-тақырып. Анықтауыштар. Кері матрица. Сызықтық теңдеулер жүйесі . Лекция жоспары: 1. Матрица. Матрицаға байланысты жалпы анықтамалар. Матрицаларға амалдар қолдану: матрицаларды қосу, матрицаларды көбейту. Квадратты матрицалар. 2. Анықтауыштар. Анықтауыштар қасиеттері. Минор және алгебралық толықтауыштар. Лекцияның қысқаша мазмұны: Екінші ретті анықтауыш деп 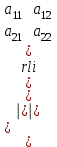 санын айтады.Үшінші ретті анықтауыш деп 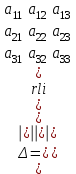 түрінде анықталған санды айтады. Барлық жатық жолдарын сәйкес тік жолдарымен ауыстарғаннан анықтауыштың шамасы өзгермейді. Анықтауыштардың кез келген екі жатық не екі тік жолдарын ауыстырғанда анықтауыштардың тек таңбасы ғана өзгереді.  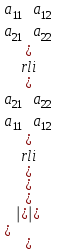 Егер анықтауыштардың екі жатық жолы немесе екі тік жолы бірдей болса, онда анықтауыштың шамасы нөлге тең. Анықтауыштың бір жатық жолының не тік жолының ортақ көбейткішін оның алдына шығаруға болады. 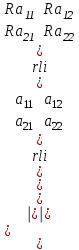 Егер анықтауыштың бір жатық жол не тік жолының барлық элементтері нөлге тең болса, мұндай анықтауыш шамасы нөлге тең. Егер анықтауыштың бір жатық жол не тік жолының әрбір элементіне онымен параллель екінші жатық, не тік жолдың сәйкес элементін бір санға көбейтіп қосса, онда анықтауыштың шамасы өзгермейді.  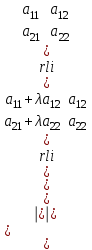 Анықтауыштың бір жатық не тік жолының әрбір элементін өзінің сәйкес алгебралық толықтауышына көбейтіп қоссақ, онда қосынды анықтауыш шамасына тең болады. 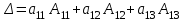 Егер анықтауыштың бір жатық жолының элементін осы жатық жолмен параллель екінші жолдың сәйкес келетін элементінің алгебралық толықтауышына көбейтіп қоссақ, онда қосынды нөлге тең болады. 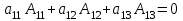 Анықтама 1. Анықтауыштың 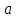 ij элементінің миноры деп анықтауыштағы і-жатық жолмен, j-тік жолдың элементтерін сызып тастағанда пайда болған анықтауышты айтады. ij элементінің миноры деп анықтауыштағы і-жатық жолмен, j-тік жолдың элементтерін сызып тастағанда пайда болған анықтауышты айтады.Анықтама 2. Анықтауыштың 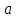 ij элементінің алгебралық толықтауышы Аij келесі түрде анықталады: ij элементінің алгебралық толықтауышы Аij келесі түрде анықталады: 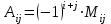 . .m-жатық жолдан және n-тік жолдан тұратын сандардан құралған тікбұрышты кесте матрица деп аталады. Матрица 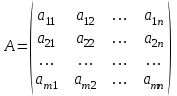 түрінде жазылады немесе қысқаша түрде 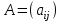 , мұндағы , мұндағы 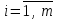 (яғни i=1, 2, 3,…,m) - жатық жол нөмірі, (яғни i=1, 2, 3,…,m) - жатық жол нөмірі, 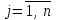 (яғни j=1, 2, 3,…,n) – тік жол нөмірі. (яғни j=1, 2, 3,…,n) – тік жол нөмірі. Ал А матрицасын 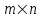 өлшемді матрица деп атайды және өлшемді матрица деп атайды және 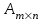 деп жазады. Матрицалар құралған деп жазады. Матрицалар құралған 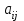 саны матрицаның элементтері деп аталады. Жоғары бұрышынан шығатын диагональда орналасқан элементтері бас диагональды құрайды. саны матрицаның элементтері деп аталады. Жоғары бұрышынан шығатын диагональда орналасқан элементтері бас диагональды құрайды. Егер екі матрицаның барлық сәйкес келетін элементтері тең болса, онда мұндай матрицалар өзара тең болады, яғни A=B, егер 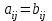 , мұнда , мұнда 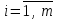 , , 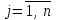 . .Егер матрицаның жатық жолдар саны тік жолдар санына тең болса, ондай мұндай матрицаны – квадрат матрица деп атайды. 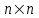 өлшемді квадрат матрицаны n өлшемді квадрат матрица деп атайды. өлшемді квадрат матрицаны n өлшемді квадрат матрица деп атайды. Бас диагоналінің элементтерінен басқа элементтерінің бәрі нөлге тең квадрат матрица диагональдық матрица деп аталады. Бас диагональдің элементтерінің барлығы бірдей бірге тең диагональдық матрица бірлік матрица деп аталады. Бірлік матрица Е әрпімен белгіленеді. Егер квадрат матрицаның бас диагоналінің бір жағында орналасқан элементтерінің барлығы нөлдер болса, онда мұндай матрица үшбұрышты матрица деп аталады. Барлық элементтері нөльге тең матрица нөлдік матрица деп аталады. Нөлдік матрица О әрпімен белгіленеді: 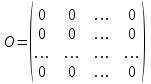 Матрицалық есептеулерде О және Е матрицалары арифметикада 0 және 1 сандары рөлін атқарады. Бір жатық жолдан немесе бір тік жолдан тұратын матрица векторлық деп аталады (немесе тік жол матрица немесе жатық жол) жалпы түрі: 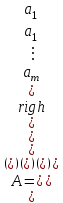 , , 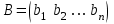 . .Бір санынан тұратын 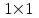 өлшемді матрица сол санға теңестіріледі, яғни өлшемді матрица сол санға теңестіріледі, яғни 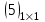 5-ке тең. 5-ке тең. Егер матрицаның барлық жатық жолдарын сәйкес сол нөмерлерімен тік жол етіп ауыстырғаннан шыққан матрица транспозицияланған матрица деп атайды. Оны АТ деп белгілейді. Матрицалардың қарапайым түрленуі матрицаның екі параллель қатарының орындарын ауыстыру. матрицаның қатарының барлық элементтерін нөлге тең емес санға көбейту матрица қатарының барлық элементтеріне параллель қатардың сәйкес элементтерін бір санға көбейтіп қосу. А және В матрицалары эквивалент матрицалар деп аталады, егер оның біреуі екіншісін элементар түрлендіру арқылы алынса. Кез-келген матрицаны элементар түрлендірулер арқылы бас диагональдарында бірлер, қалған элементтері нөлге тең матрицасына келтіруге болады. Мұндай матрицаны канондық (қарапайым) матрица деп атайды, мысалы: Ұсынылатын әдебиеттер Айдос Е.Ж. «Жоғары математика», Оқулық.-Алматы; «Иль Тех Кітап» ЖШС, 2003ж-744б. Әшірбаев Х.А., Такибаева Г.А. «Математикалық талдау»-Шымкент, 2010ж. Данилов Ю.М., Журбенко Л.Н., Никонова Г.А. «Математика», Учебное пособие для студентов вузов. М.: ЮНИТИ-ДАНА, 2006. Данко П.Е., Попов А.Г., Кожевникова Т.Я. «Высшая математика в упражнениях и задачах», Учебное пособие для студентов втузов. Ч.1.-М.:ВШ, 2003г.-415с. СӨЖ-ге арналған бақылау тапсырмалары Есептер № АЗ-1.4; [10, том 1] ЖҮТ 1.2; [10, том 1, беттер 42-49] 2-тақырып. Анықтауыштар. Кері матрица. Сызықтық теңдеулер жүйесі Лекция жоспары: Сызықтық теңдеулер жүйесі. Крамер формулалары. Кері матрицаның көмегімен теңдеулер жүйесін шешу Лекцияның қысқаша мазмұны: Сызықтық теңдеулер жүйесі. Крамер формулалары. Кері матрицаның көмегімен теңдеулер жүйесін шешу 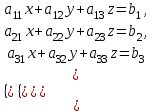 жүйесінің анықтауышы нөлге тең болмаған жағдайда бір ғана шешуі болады. Бұл жүйені екі әдіспен шешуге болады. 1.Крамер формулалары арқылы шешу Егер ∆ анықтауышы нөлге тең болмаса, онда 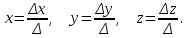 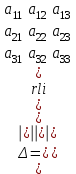 , , 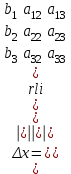 , ,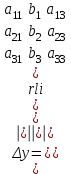 , , 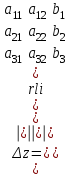 . .Аmn матрицасы деп m жатық және n тік жолы бар тіктөртбұрышты кесте құрайтын сандар жиынын айтады. 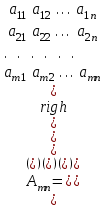 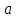 ij,i=1m, j=1n – матрица элементтері. ij,i=1m, j=1n – матрица элементтері.Егер m=n болса, онда матрица квадрат матрица деп аталады. Өлшемдері бірдей матрицаларды қосуға болады. С=А±В (Cij= 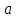 ij± ij±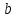 ij) ij)2) А матрицасын бір санға көбейту үшін сол санға матрицаның барлық элементтерін көбейтеді. Мысалы: А матрицасын 3-ке көбейтейік: 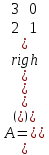 , , 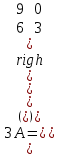 . .3) Матрицаларды көбейту. Аmn және Вnp матрицаларының көбейтіндісі деп элементтері 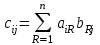 болатын сmp= (AB)mpматрицасын айтады.Жалпы алғанда АВ≠BA А матрицасына кері матрица А-1 депАА-1=А-1А=Е теңдігін қанағаттандыратын матрицаны айтады. Е-бірлік матрица. А матрицасына кері матрица болу үшін А матрицаның анықтауышы нөлден өзгеше болу керек. 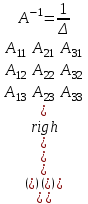 , ,мұндағы ∆-A матрицасының анықтауышы, Аij-А матрицасының 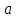 ij элементтерінің алгебралық толықтауыштары. ij элементтерінің алгебралық толықтауыштары.2.Теңдеулер жүйесін матрицалық әдіспен шешу Егер 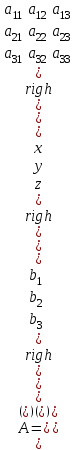 Онда сызықтық теңдеулер системасы келесі түрде жазылады: АХ=В Егер А-1 кері матрица болса, онда Х=А-1В. Теорема Ерекше емес матрицаның кері матрицасы болады. 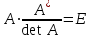 және және 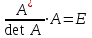 . . Шыққан қортындыларды (3.1) анықтамасымен салыстыра келесі өрнекті аламыз: Шыққан қортындыларды (3.1) анықтамасымен салыстыра келесі өрнекті аламыз: 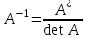 , яғни , яғни 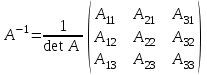 . .Кері матрицаның қасиеттері: 1. 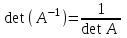 ; ;2. 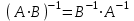 ; ;3. 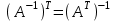 . .Ұсынылатын әдебиеттер 1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004. 2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969. 3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004. 4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005. СӨЖ-ге арналған бақылау тапсырмалары ЖҮТ 1.1; [10, том.1, беттер 33-38] Есептер: АЗ-1.1; АЗ-1.2; АЗ-1.3; [10, том 1] СӨЖ-ге арналған бақылау тапсырмалары Есептер № АЗ-1.4; [10, том 1] ЖҮТ 1.2; [10, том 1, беттер 42-49] ІІ бөлім. Векторлық алгебра 3-тақырып.Векторлар,оларға қолданылатын амалдар. Векторлардың көбейтінділері Лекция жоспары 1. Векторлар және оларға сызықтық амалдар қолдану; 2. Векторлардың скалярлық көбейтіндісі және оның механикалық мағынасы, екі вектордың ортогональды шарты; 3. Векторлардың векторлық көбейтіндісіжәне оның геометриялық, механикалық мағыналары, қасиеттері; 4. Үш вектордың аралас көбейтіндісі.Үш вектрордың компланарлық шарты. Лекцияның қысқаша мазмұны: Бағытталған кесіндіні вектор деп атайды. Басы А нүктесі, ұшы В нүктесі болатын бағытталған кесіндіні 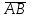 символымен немесе бір әріппен мысалы, символымен немесе бір әріппен мысалы,  , ,  деп белгілейді. Вектордың координаталары деп белгілейді. Вектордың координаталары  ={x,y,z} немесе ={x,y,z} немесе  =xi+yj+zk. =xi+yj+zk.Егер А (х1,у1,z1) және В (х2,у2,z2) нүктелері берілсе, онда АВ векторының координаталары оның ұшы В координаталарынан бас нүктеі А-ның сәйкес координаталарын алу арқылы анықталады: 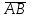 ={x2-x1,y2-y1,z2-z1}. Вектордың ұзындығы | ={x2-x1,y2-y1,z2-z1}. Вектордың ұзындығы |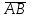 | немесе | немесе 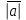 деп белгіленеді және вектордың модулі деп аталады. деп белгіленеді және вектордың модулі деп аталады.| 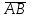 |= |=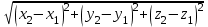 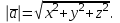 Басы мен ұшы беттесіп келетін вектор нөлдік вектор деп аталады. Ұзындығы бірге тең вектор бірлік вектор деп аталады. Бір немесе параллель түзуде жататын векторлар коллинеар векторлар деп аталады.  =(x1,y1,z1) және =(x1,y1,z1) және  =(x2,y2,z2) векторларының коллинеар болу шарты: =(x2,y2,z2) векторларының коллинеар болу шарты: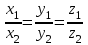 Бір немесе параллель жазықтықта жатса, онда ол векторлар компланар векторлар деп аталады.Егер  мен мен  векторлары бірдей бағытталған және модульдары бірдей болса, онда олар тең векторлар деп аталады. векторлары бірдей бағытталған және модульдары бірдей болса, онда олар тең векторлар деп аталады.Векторларды қосу үшін үшбұрыш немесе параллелограмм әдістері қолданылады.  ={xa,ya,za}, ={xa,ya,za},  ={xв,yв,zв} векторлары берілсін. Онда ={xв,yв,zв} векторлары берілсін. Онда + + = =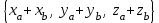  - - = = 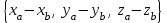 R  = = 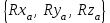 Берілген а векторының OX,OУ,OZ осьтерімен жасайтын бұрыштарын α, β, γ деп белгілейік. Бұл бұрыштар вектордың бағытын анықтайды.Вектордың бағыттауыш косинустары: 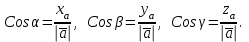 Бағыттауыш косинустары арасындағы байланыс cos2α + cos2β+ cos2γ=1.  векторының ОХ осіне проекциясы осы вектордың модулін вектор мен осьтің арасындағы бұрыштың косинусына көбейткенге тең векторының ОХ осіне проекциясы осы вектордың модулін вектор мен осьтің арасындағы бұрыштың косинусына көбейткенге тең прох  =| =| |cosφ. |cosφ.Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусының көбейтіндісіне тең болатын санды айтады және  · ·  немесе ( немесе (  ) деп белгіленеді. Анықтама бойынша ) деп белгіленеді. Анықтама бойынша  · ·  =| =| | | | | | cosφ. | cosφ.  · ·  = = · ·  · ·  =| =| |·пр |·пр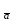  =| =| | пр | пр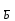  (  + + )· )· = = · · + + · · (λ   )=λ( )=λ( · ·  ) )Егер  және және  векторлары перпендикуляр болса, онда олардың скалярлық көбейтіндісі нөлге тең векторлары перпендикуляр болса, онда олардың скалярлық көбейтіндісі нөлге тең  · ·  =0 =0Егер  ={xa,ya,za} және ={xa,ya,za} және ={xв,yв,zв} векторлары берілсе, онда олардың скалярлық көбейтіндісі ={xв,yв,zв} векторлары берілсе, онда олардың скалярлық көбейтіндісі  · ·  =xa xb+ya yb+za zb =xa xb+ya yb+za zbЕгер екі вектор арасындағы бұрышты φ деп белгілесек, онда 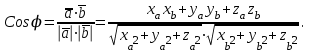  мен мен  векторларының векторлық көбейтіндісі деп келесі түрде анықталған векторларының векторлық көбейтіндісі деп келесі түрде анықталған  векторын айтамыз. векторын айтамыз.1.  = =    вектордың ұзындығы | вектордың ұзындығы |   |=| |=| | | | | | sin φ=| | sin φ=| |. а мен в векторларынан салынған параллелограмм ауданына тең. |. а мен в векторларынан салынған параллелограмм ауданына тең.2.  = =    → →    , ,    , яғни , яғни  мен мен  векторлар жазықтығына перпендикуляр векторлар жазықтығына перпендикуляр3. [    ] векторлары ұшынан қарағанда ] векторлары ұшынан қарағанда  дан дан  -ға бұрылу бағыты сағат тіліне қарсы болуы керек. -ға бұрылу бағыты сағат тіліне қарсы болуы керек.Егер  және және  коллинеарлы болса, онда коллинеарлы болса, онда    =0 =0   =- =-   (λ  ) )  = λ = λ   (  + + ) )  = =   + +   Егер  және және  векторлары координаталары арқылы берілсе, яғни векторлары координаталары арқылы берілсе, яғни  = = 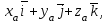  = = 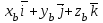 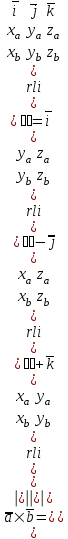  Үш  , , , , векторлардың аралас көбейтіндісі деп векторлардың аралас көбейтіндісі деп  және және  векторлық көбейтіндісін векторлық көбейтіндісін  векторымен скаляр көбейткендегі санды айтады. Векторларды аралас көбейту ( векторымен скаляр көбейткендегі санды айтады. Векторларды аралас көбейту (   ) · ) · немесе немесе 1) Vпарал/пед=  · ·  · · Vпр/да= Vпр/да=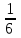 | | · ·  · · | |2) Көбейткіштерді айнала ауыстырудан аралас көбейтіндінің шамасы өзгермейді.    · · = =   · · = =   · · 3) Кез келген екі көбейткішті ауыстырып қоюдан аралас көбейтіндінің таңбасы кері өзгереді.    =- =-   4) Егер көбейткіш векторлар компланарлы болса, онда аралас көбейтінді нөлге тең:    · · =0 =0Егер  , ,  , ,  векторлары координаталары арқылы берілсе, векторлары координаталары арқылы берілсе,  ={xa,ya,za}, ={xa,ya,za},  ={xв,yв,zв}, ={xв,yв,zв},  = {xc, yc, zc}, онда осы векторлардың аралас көбейтіндісі келесі формуламен анықталады = {xc, yc, zc}, онда осы векторлардың аралас көбейтіндісі келесі формуламен анықталады    · ·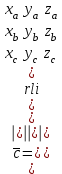 . . , , , , векторларының компланарлы болу шарты векторларының компланарлы болу шарты 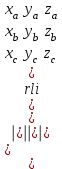 =0. =0.Ұсынылатын әдебиеттер 1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004. 2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969. 3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004. 4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005. СӨЖ-ге арналған бақылау тапсырмалары ЖҮТ 2.1; ЖҮТ 2.2; [10, том 1, беттер 69-85] Есептер: АЗ-2.1; АЗ-2.2; АЗ-2.3; [10, том 1] |
