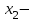Лекция жоспары
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
8-тақырып. Функцияны оның туындысы арқылы зерттеу(2 сағ. ) Лекция жоспары: 1.Функцияның монотондық белгілері; 2. Функцияның экстремумының бар болуының жеткілікті шарттары. Қисықтың ойысты және дөңесті бөліктері. Иілу нүктелері. Қисықтың асимптоталары; 3. Функцияны зерттеу мен графигін салудың жалпы схемасы. Лекцияның қысқаша мазмұны Функцияның өсуі мен кемуі Туындының қосымшаларының бірі оның функцияны зерттеуді, оның графигін салуда қолдану болып табылады. Теорема. Егер 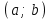 интервалында дифференциалданатын интервалында дифференциалданатын 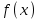 функциясы өсетін (кемитін) болса, онда функциясы өсетін (кемитін) болса, онда 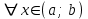 үшін үшін 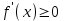 ( (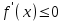 ). ).Теорема. (жеткілікті шарт). Егер 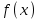 функциясы функциясы 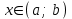 үшін үшін 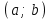 интервалында дифференциалданса және интервалында дифференциалданса және 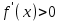 ( (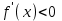 ) болса, онда осы функция ) болса, онда осы функция 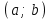 интервалында өседі (кемиді). интервалында өседі (кемиді).Функцияның максимумы мен минимумы Егер 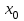 нүктесінің нүктесінің 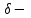 маңайы бар болып, осы маңайдың барлық маңайы бар болып, осы маңайдың барлық 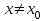 үшін үшін 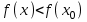 теңсіздігі орындалса, теңсіздігі орындалса, 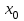 нүктесі нүктесі 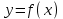 функциясының максимум нүктесі деп аталады. функциясының максимум нүктесі деп аталады.
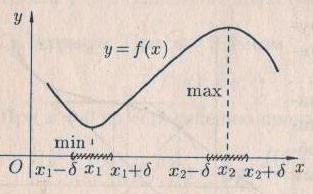
Максимум (минимум) нүктедегі функция мәні функцияның максимум (минимумы) деп аталады. Функцияның максимумы (минимумы) функцияның экстремумы деп аталады. Экстремум ұғымы функцияның анықталу облысында жататын, нүктенің белгілі бір маңайымен байланысты. Сондықтан, функцияның анықталу облысының ішкі нүктесінде ғана экстремумы болуы мүмкін. Функция экстремумының бар болу шартын қарастырайық. Теорема. (экстремумның қажетті шарты). Егер 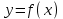 дифференциалданатын функциясының дифференциалданатын функциясының 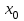 нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең: нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең: 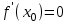 . Осылайша, үзіліссіз функцияның тек туындысы нөлге немесе туындысы болмайтын нүктелерінде ғана экстремумы болады. Осындай нүктелерді күдікті нүктелер деп атайды. . Осылайша, үзіліссіз функцияның тек туындысы нөлге немесе туындысы болмайтын нүктелерінде ғана экстремумы болады. Осындай нүктелерді күдікті нүктелер деп атайды. Теорема 25.9. (экстремумның жеткілікті шарты). Егер 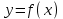 функциясы функциясы 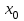 күдікті нүктесінің қандай да күдікті нүктесінің қандай да 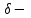 маңайында дифференциалданатын болса, және одан өткенде (солдан оңға) маңайында дифференциалданатын болса, және одан өткенде (солдан оңға) 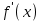 туындысы плюстен минусқа ауысса, туындысы плюстен минусқа ауысса, 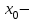 максимум нүкте, минустан плюске ауысса, максимум нүкте, минустан плюске ауысса, 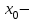 минимум нүкте. минимум нүкте.Теорема 25.10. Егер 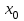 нүктесінде нүктесінде 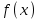 функциясының бірінші туындысы нөлге тең функциясының бірінші туындысы нөлге тең 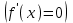 , ал , ал 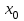 нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса 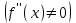 , онда , онда 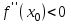 болғанда болғанда 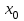 нүктесінде функция максимумға ие, ал нүктесінде функция максимумға ие, ал 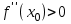 болғанда минимумға ие. болғанда минимумға ие.Функция графигінің дөңестігі, иілу нүктелері Егер 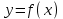 дифференциалданатын функциясының графигі оған жүргізілген кез-келген жанамадан жоғары болса, онда график – төменнен дөңес деп, егер жанамадан төмен болса, график – жоғарыдан дөңес деп аталады. Үзіліссіз дифференциалданатын функциясының графигі оған жүргізілген кез-келген жанамадан жоғары болса, онда график – төменнен дөңес деп, егер жанамадан төмен болса, график – жоғарыдан дөңес деп аталады. Үзіліссіз 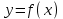 функциясының дөңестігі әртүрлі бөліктерін ажыратып тұратын нүкте – иілу нүктесі деп аталады. функциясының дөңестігі әртүрлі бөліктерін ажыратып тұратын нүкте – иілу нүктесі деп аталады. Теорема 25.11. Егер 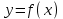 функциясының функциясының 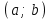 интервалының барлық нүктесінде екінші туындысы теріс, яғни интервалының барлық нүктесінде екінші туындысы теріс, яғни 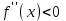 болса, онда осы интервалда функция графигі жоғарыдан дөңес. Егер болса, онда осы интервалда функция графигі жоғарыдан дөңес. Егер 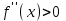 , , 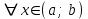 болса, функция графигі төменнен дөңес. болса, функция графигі төменнен дөңес.Теорема 25.12. (иілу нүктелерінің бар болуының жеткілікті шарты). Егер 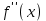 екінші ретті туынды екінші ретті туынды 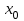 нүктесі арқылы өткен де, (бұл нүктеде ол нөльге тең немесе болмайды), таңбасын өзгертсе, онда графиктің абсцисссасы нүктесі арқылы өткен де, (бұл нүктеде ол нөльге тең немесе болмайды), таңбасын өзгертсе, онда графиктің абсцисссасы 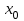 болатын графиктің нүктесі иілу нүктесі болады. болатын графиктің нүктесі иілу нүктесі болады. Асимптоталар. 6-анықтама: Егер 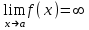 болса, онда х=а түзуі у=f(x) функциясының вертикаль асимптотасы деп атайды. Вертикаль асимптотаны у=f(x) функциясының үзіліс нүктелері арасынан іздеу керек. Үзіліссіз функциялардың графигінде вертикаль асимпотасы болмайды (көпмүше болған жағдайда). у=f(x) функциясының х шексіздікке ұмтылғанда y=kx+b түзуі көлбеу асимптота деп аталады, егер. болса, онда х=а түзуі у=f(x) функциясының вертикаль асимптотасы деп атайды. Вертикаль асимптотаны у=f(x) функциясының үзіліс нүктелері арасынан іздеу керек. Үзіліссіз функциялардың графигінде вертикаль асимпотасы болмайды (көпмүше болған жағдайда). у=f(x) функциясының х шексіздікке ұмтылғанда y=kx+b түзуі көлбеу асимптота деп аталады, егер.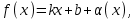 мұнда мұнда 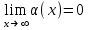 Егер y=kx+b көлбеу асимптота бар болса, онда k және b коэффициенттері мына формулалармен анықталады. 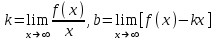 Егер k=0 болса, көлбеу асимптотаны горизонталь асимптота деп атайды. Функцияны зерттеу және графигін салу у=f(x) функциясының графигін салу үшін,келесі зерттеу схемасы ұсынылады. Функцияның анықталу және мәндер облыстарын табу. Функцияның жұп, тақ және периодты екендігін анықтау. Функцияның үзіліс нүктесін анықтау. Вертикаль және көлбеу асимптоталарын анықтау. Функцияның өспелі және кемімелі болатын аралықтарын және экстремумдарын анықтау. Функцияның ойыс және дөңес болатын аралықтарын табу, иілу нүктелерін табу керек. ОХ осімен қиылысу нүктелерін табу және басқада қосымша нүктелерін анықтау. Осы алынған нұсқаулардың көмегімен функция графигінің эскизін салу керек. Негізгі әдебиет тізімі 1. Привалов И.И. Аналитическая геометрия, М: Гос. изд-во Юрайт, 2017. 2. Шаихова Г.С., Қасымова Л. Ж. Жоғары математика. І-бөлім., Қарағанды, ҚарМТУ баспасы, 2019. 3. Шаихова Г.С., Дүйсебаева. Д. О.Анықтамаған интегралда. Анықталған интегралдардың қолданылуы. Қарағанды, ҚарМТУ баспасы, 2018. 4. Шаихова Г.С., Қасымова Л. Ж. Еселі интегралдар. Қарағанды, ҚарМТУ баспасы, 2019. 5. Мустафина Л.М. Высшая математика для студентов технических специальностей. Часть 2: Введение в математический анализ. Дифференциальное и интегральное исчисление функций одной переменной. Изд-во КарГТУ, Караганда, 2017. 6. Мустафина Л.М., Абаева Н.Ф. Высшая математика для студентов технических специальностей. Часть 3: Функции многих переменных. Кратные интегралы. Дифференциальные уравнения. Изд-во КарГТУ, Караганда, 2017. 7. Мустафина Л.М., Абаева Н.Ф. Высшая математика для студентов технических специальностей. Часть 4: Ряды. Элементы теории вероятностей и математической статистики. Изд-во КарГТУ, Караганда, 2018. 8. Клетеник Д.В. Сборник задач по аналитической геометрии, Спб.: Лань, 2019. 9. Рябушко А.П., Индивидуальные задания по высшей математике: Т-1,2, 3, Минск: Высшая школа, 2013. 10. Данко П.Е. и др. Высшая математика в упражнениях и задачах, т.1-2., М.: Мир и образование, 2016. 11. Берман Н.Г. Сборник задач по курсу математического анализа: Учебное пособие, Спб.: Лань, 2019. 12. Запорожец Г.И. Руководство к решению задач по математическому анализу, Спб.: Лань, 2010. 13. Тутанов С.К., Шаихова Г.С. Жоғары математика, В 2 ч. 1 – бөлім. ҚарМТУ баспасы. – Қарағанды, 2011. – 99 б. Қосымша әдебиет тізімі 1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: т.1-3. Спб.: Лань, 2018 2. Бутузов В.Ф. и др. Математический анализ в вопросах и задачах: Учебное пособие для вузов, Спб.: Лань, 2010. 3. Лунгу К.Н. Сборник задач по высшей математике с контрольными работами, М.: Айрис-пресс, 2013. 4. Шаихова Г.С., Махметова Г. Ш. Қатарлар. Қарағанды, ҚарМТУ баспасы, 2018. 5. Шаихова Г.С., Махметова Г. Ш. Бір айнымалы функциялардың дифференциалдық есептеулері. Қарағанды, ҚарМТУ баспасы, 2019. |

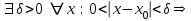
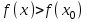 болса,
болса, 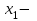 минимум нүктесі,
минимум нүктесі,