Лекция жоспары
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
β(х) символдарымен белгілейді. |
| | 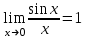 | |
шегі қолданылады. Бұл шек былай оқылады: аргументі нөлге ұмтылғандағы синустың аргументіне қатынасының шегі бірге тең.
Екінші тамаша шек
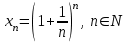 сандық тізбегінің шегі е-ге тең (15.6):
сандық тізбегінің шегі е-ге тең (15.6):| | 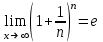 . . |
Функцияның интервалдағы және кесіндідегі үзіліссіздігі
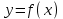 функциясы
функциясы 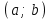 интервалында үзіліссіз деп аталады, егер ол осы интервалдың әрбір нүктесінде үзіліссіз болса.
интервалында үзіліссіз деп аталады, егер ол осы интервалдың әрбір нүктесінде үзіліссіз болса. 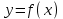 функциясы
функциясы 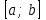 интервалында үзіліссіз деп аталады, егер ол
интервалында үзіліссіз деп аталады, егер ол 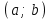 интервалында үзіліссіз және
интервалында үзіліссіз және 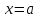 нүктесінде оң жақтан, ал
нүктесінде оң жақтан, ал 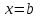 нүктесінде сол жақта үзіліссіз болса.
нүктесінде сол жақта үзіліссіз болса. Функцияның үзіліс нүктелері мен олардың жіктелуі
Функция үзіліссіздігі бұзылатын нүктелер функцияның үзіліс нүктелері деп аталады. Егер
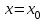 нүктесі
нүктесі 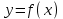 функциясының үзіліс нүктесі болса, онда бұл функцияда функция үзіліссіздігінің бірінші анықтамасынан ең болмағанда бір шарты орындалмайды, атап айтқанда:
функциясының үзіліс нүктесі болса, онда бұл функцияда функция үзіліссіздігінің бірінші анықтамасынан ең болмағанда бір шарты орындалмайды, атап айтқанда:Функция барлық үзіліс нүктелер бірінші, екінші текті үзіліс нүктелеріне жіктеледі.
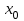 нүктесі бірінші текті үзіліс нүктесі деп аталады, егер осы нүктеде функцияның оң, сол нақты ақырлы шектері (бір жақты) бар болса, онда
нүктесі бірінші текті үзіліс нүктесі деп аталады, егер осы нүктеде функцияның оң, сол нақты ақырлы шектері (бір жақты) бар болса, онда 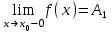 және
және 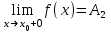 . Сонымен қатар,
. Сонымен қатар, а) егер
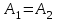 болса, онда
болса, онда 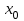 -қалыпта келтірілетін үзіліс нүктесі, ә) егер
-қалыпта келтірілетін үзіліс нүктесі, ә) егер 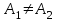 болса, онда
болса, онда 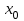 -ақырлы үзіліс нүктесі деп аталады, егер
-ақырлы үзіліс нүктесі деп аталады, егер 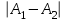 шамасын бірінше текті үзіліс нүктесіндегі секіріс деп аталады.
шамасын бірінше текті үзіліс нүктесіндегі секіріс деп аталады. Егер
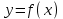 функциясының ең болмағанда біржақты шектерінің (оң және сол жақты) біреуі жоқ болса немесе шексіздікке тең болса,
функциясының ең болмағанда біржақты шектерінің (оң және сол жақты) біреуі жоқ болса немесе шексіздікке тең болса, 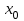 нүктесі
нүктесі 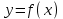 функциясының екінші текті үзіліс нүктесі деп аталады.
функциясының екінші текті үзіліс нүктесі деп аталады. Үзіліссіз функциялар туралы негізгі теоремалар. Элементар
функциялардың үзіліссіздігі
Теорема. Екі үзіліссіз функцияның қосындысы, көбейтіндісі, бөліндісі үзіліссіз функция (бөлімінің бөлімі 0-ге тең болатын, аргумент мәнінен өзге).
Теорема.
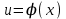 функциясы
функциясы 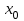 нүктесінде, ал
нүктесінде, ал 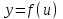 функциясы
функциясы 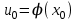 нүктесінде үзіліссіз болсын. Сонда үзіліссіз функциядан құралған күрделі
нүктесінде үзіліссіз болсын. Сонда үзіліссіз функциядан құралған күрделі 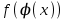 функциясы
функциясы 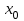 нүктесінде үзіліссіз.
нүктесінде үзіліссіз. Ұсынылатын әдебиеттер
1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004.
2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969.
3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004.
4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005.
СӨЖ-ге арналған бақылау тапсырмалары
ЖҮТ 5.1; [10, том 1, беттер 166-176]
Есептер: АЗ-5.1; АЗ-5.2; [10, том 1]
ЖҮТ 5.2; [10, том 1, беттер 178-184]
Есептер: АЗ-5.3; АЗ-5.4; [10, том 1]
IV бөлім.Бір айнымалы функциясын дифференциалдық есептеу(4 сағ.)
7-тақырып. Бір айнымалы функцияның дифференциалдық есептеу (2сағ.).
Лекция жоспары:
Туынды, туынды ұғымына әкелетін есептер. Туындының геометриялық мағынасы;
Логарифмдік дифференциалдау, күрделі, дәрежелік және көрсеткіштік функцияларды дифференциалдау формулалары;
Функцияның дифференциалы, оның туындымен байланысы. Дифференциалдың геометриялық мағынасы. Дифференциалды жуықтап есептеуге қолдану;
Жоғары ретті дифференциалдар мен туындылар. Маклорен формуласы;
Лекцияның қысқаша жазбасы
у=f(x) функциясы х0нүктесінің қандай да бір маңайында анықталған. Осы функцияның х0 нүктесіндегі өсімшесі деп
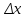 айнымалысы функциясын айтады:
айнымалысы функциясын айтады: 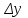 =f(x0+
=f(x0+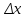 )-f(x0).
)-f(x0).Анықтама. Егер
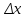 нөлге ұмытылғанда функция өсімшесі мен аргумент өсімшесі қатынасының шегі бар болса, онда бұл шек берілген функцияның х0 нүктесіндегі туындысы деп аталады. Сонымен, егер
нөлге ұмытылғанда функция өсімшесі мен аргумент өсімшесі қатынасының шегі бар болса, онда бұл шек берілген функцияның х0 нүктесіндегі туындысы деп аталады. Сонымен, егер 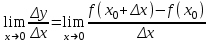 бар болса, оны берілген функцияның х0 нүктесіндегі туындысы деп атайды.
бар болса, оны берілген функцияның х0 нүктесіндегі туындысы деп атайды.Туындыны мынадай символдармен белгілейді f
 (x0), y
(x0), y (x0) немесе
(x0) немесе 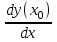 .
.Туындыны табу операциялары дифференциалдау деп аталады.
| 1. 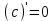 2. 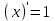 3. 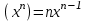 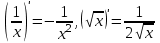 4. 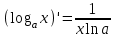 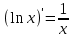 5. 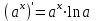 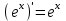 6. 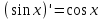 7. 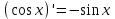 | 8. 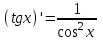 9. 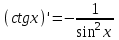 10. 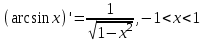 11. 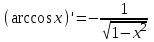 12. 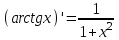 13. 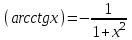 |
Егер u(x) және v(x) функцияларының х0нүктесінде туындылары бар болса, олардың алгебралық қосындысының, көбейтіндісінің және қатынасының (v(x0)≠0) x0 нүктесінде туындылары бар болады және мына формулалар бойынша табылады:
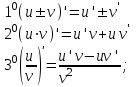
Күрделі функциялардың туындысы:
Егер u=u(x) функцияcының х0нүктесінде туындысы бар болса: u0=φ’(х0) ал у=f(u) функциясының u0=φ(х0) нүктесінде туындысы бар болса, онда х0 нүктесінде y=f(φ(х))=F(x) функциясыныңда туындысы бар болады және мынаған тең
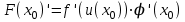 немесе
немесе 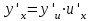 .
.Айқындалмаған түрде берілген функция
Егер функция
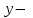 ке қатысты шешілген
ке қатысты шешілген 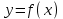 түрінде берілсе, функция айқындалған түрде берілген дейміз.
түрінде берілсе, функция айқындалған түрде берілген дейміз. Айқындалмаған түрде берілген функция деп
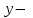 ке қатысты шешілмеген,
ке қатысты шешілмеген, 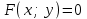 түрінде берілген функция түсіндіріледі.
түрінде берілген функция түсіндіріледі.Кез-келген
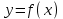 айқындалған функцияны
айқындалған функцияны 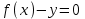 теңдеуімен берілген айқындалмаған функция түрінде жаза аламыз, бірақ керісінше жаза алмаймыз. Егер айқындалмаған функция
теңдеуімен берілген айқындалмаған функция түрінде жаза аламыз, бірақ керісінше жаза алмаймыз. Егер айқындалмаған функция 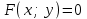 түрінде берілсе,
түрінде берілсе, 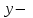 тан
тан 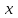 бойынша туынды табу үшін теңдеуді
бойынша туынды табу үшін теңдеуді 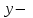 ке қатысты шешу қажет емес: ол үшін
ке қатысты шешу қажет емес: ол үшін 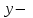 ті
ті 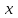 -тан тәуелді деп алып, берілген теңдеуді
-тан тәуелді деп алып, берілген теңдеуді 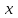 бойынша дифференциалдап, алынған теңдеуді
бойынша дифференциалдап, алынған теңдеуді 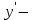 қа қатысты шешу жеткілікті.
қа қатысты шешу жеткілікті.Параметрлік түрде берілген функция
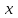 аргументі мен
аргументі мен 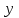 функциясы арасындағы байланыс параметрлік түрде екі теңдеу түрінде берілген болсын:
функциясы арасындағы байланыс параметрлік түрде екі теңдеу түрінде берілген болсын: 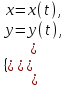 мұндағы
мұндағы 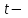 параметр деп аталатын көмекші айнымалы. функциясының туындысы бар деп алып және
параметр деп аталатын көмекші айнымалы. функциясының туындысы бар деп алып және 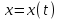 функциясының кері
функциясының кері 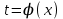 функциясы бар деп алып,
функциясы бар деп алып, 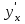 туындысын табайық. Кері функцияны дифференциалдау ережесі бойынша
туындысын табайық. Кері функцияны дифференциалдау ережесі бойынша 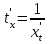 параметрлік түрде берілген
параметрлік түрде берілген 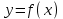 функциясын
функциясын 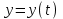 , мұндағы
, мұндағы 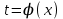 болатын күрделі функция түрінде қарастыруға болады.
болатын күрделі функция түрінде қарастыруға болады. Туындыны табу үшін бірқатар жағдайларда, алдымен берілген функцияны логарифмдейді. Кейіннен, алынған нәтижені дифференциалдайды. Осылай орындалған амалды – логарифмдік дифференциалдау деп аталады. Туындысы тек логарифмдік дифференциалдау арқылы табылатын функциялар бар. Солардың бірі
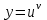 дәреже-көрсеткіштік функциясы, мұндағы
дәреже-көрсеткіштік функциясы, мұндағы 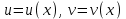 функциялары
функциялары 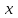 бойынша дифференциалданатын функциялар. Осы функцияның туындысын табайық:
бойынша дифференциалданатын функциялар. Осы функцияның туындысын табайық: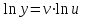 ,
, 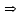
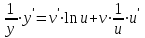 ,
, 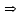
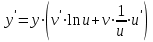 ,яғни
,яғни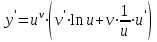 ,
, 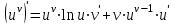 формуласын есте сақтау ережесін тұжырымдайық: дәреже – көрсеткіштік функцияның туындысы
формуласын есте сақтау ережесін тұжырымдайық: дәреже – көрсеткіштік функцияның туындысы 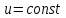 болғандағы көрсеткіштік функцияның туындысы мен
болғандағы көрсеткіштік функцияның туындысы мен 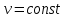 болғандағы дәрежелік функцияның туындысының қосындысына тең.
болғандағы дәрежелік функцияның туындысының қосындысына тең. 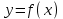 функциясының
функциясының 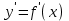 туындысы
туындысы 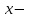 тан тәуелді функция да болып табылады, және бірінші ретті туынды деп аталады. Егер
тан тәуелді функция да болып табылады, және бірінші ретті туынды деп аталады. Егер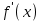 функциясы дифференциал-данатын болса, онда оның туындысы екінші ретті туынды деп аталып,
функциясы дифференциал-данатын болса, онда оның туындысы екінші ретті туынды деп аталып, 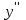 арқылы белгіленеді. Сонымен,
арқылы белгіленеді. Сонымен, 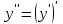 .Екінші ретті туындыдан алынған туынды бар болса, онда ол үшінші ретті туынды деп аталып,
.Екінші ретті туындыдан алынған туынды бар болса, онда ол үшінші ретті туынды деп аталып, 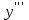 (немесе
(немесе 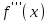 ,
, 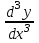 , ...) арқылы белгіленеді. Сонымен,
, ...) арқылы белгіленеді. Сонымен, 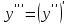 .
. 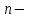 ретті туынды деп
ретті туынды деп 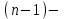 ретті туындыдан алынған туынды аталады:
ретті туындыдан алынған туынды аталады: 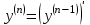 .
.Анықталмағандықтарды ашу.
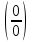 ,
, 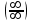 анықталмағандықтарын ашудың тәсілдерінің бірі Лопиталь ережесі болып табылады және ол келесі теоремада негізделген.
анықталмағандықтарын ашудың тәсілдерінің бірі Лопиталь ережесі болып табылады және ол келесі теоремада негізделген.Теорема:f(x) және φ(х) функциялары х=а нүктесінен басқа х=а нүктесінің маңайындағы нүктелерде дифференциалданатын және анықталған болсын және φ
 (x)≠0 болсын. Егер х
(x)≠0 болсын. Егер х а ұмтылғанда f(x) және φ(х) функциялары шексіз аз шама немесе шексіз үлкен шамалар болса және х
а ұмтылғанда f(x) және φ(х) функциялары шексіз аз шама немесе шексіз үлкен шамалар болса және х а ұмтылғанда
а ұмтылғанда 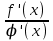 қатынастарының туындысы бар болса, онда
қатынастарының туындысы бар болса, онда 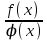 функциялары қатынасытарның шегі де бар болады және мына теңдік орындалады:
функциялары қатынасытарның шегі де бар болады және мына теңдік орындалады: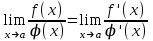 а=∞ болған жағдайда да осы ереже қолданылады.
а=∞ болған жағдайда да осы ереже қолданылады.1-ескерту:
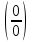 ,
,  анықталмағандықтарын ашу үшін Лопиталь ережесін бірнеше рет қолдануға болады.
анықталмағандықтарын ашу үшін Лопиталь ережесін бірнеше рет қолдануға болады.2-ескерту: Лопиталь ережесін қолданғанда қатынастарды түрлендіріп қысқартуға және шектерді есептеудің басқа да әдістеріне келтіруге болады.
Ұсынылатын әдебиеттер
1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004.
2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969.
3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004.
4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005.
СӨЖ-ге арналған бақылау тапсырмалары
ЖҮТ 6.1; ЖҮТ 6.2; ЖҮТ 6.3; [10, том 1, беттер 221-254]
Есептер АЗ-6.1; АЗ-6.2; АЗ-6.3; АЗ-6.4; АЗ-6.5; АЗ-6.6; [10, том 1]

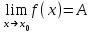 немесе
немесе 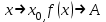 символдарымен белгілейді.
символдарымен белгілейді.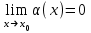 болса, онда x0 нүктесінде
болса, онда x0 нүктесінде 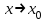 ұмтылғанда α=α(x) шексіз аз шама деп аталады.
ұмтылғанда α=α(x) шексіз аз шама деп аталады.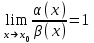 болса, онда α(x) және β(х) шексіз аз шамалары х-тің х0-ге ұмытылғанда эквивалентті шексіз аз шамалар деп аталады және xx0ұмтылғанда α(x)
болса, онда α(x) және β(х) шексіз аз шамалары х-тің х0-ге ұмытылғанда эквивалентті шексіз аз шамалар деп аталады және xx0ұмтылғанда α(x) 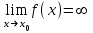 болса, онда f (x) функциясы x-x0-ге ұмытылғанда шексіз үлкен шама деп аталады.Бөлшектің алымы және бөлімі нөлге немесе шексіздікке ұмтылса, онда
болса, онда f (x) функциясы x-x0-ге ұмытылғанда шексіз үлкен шама деп аталады.Бөлшектің алымы және бөлімі нөлге немесе шексіздікке ұмтылса, онда 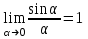 шегі бірінші тамаша шек деп аталады.
шегі бірінші тамаша шек деп аталады. .
.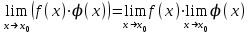 .
.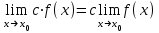 .
.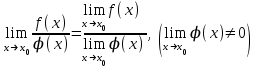 .
.