Курс лекции по геодезии. Курс лекции по геодезии Акрам, руси. Лекция по дисциплине Геодезия Лекция Определение геодезии как науки и ее задачи. История геодезии
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
|
Истинные азимуты и румб. Кроме осевого меридиана зоны при ориентировании линий местности за основное направление может приниматься направление истинного (географического) меридиана. Истинный меридиа – линия пересечения земной поверхности с плоскостью, проходящей через отвесную линию и ось вращения Земли. Положение линии местности относительно истинного меридиана определяется истинным азимутом или истинным румбом. ^ Истинный азимут линии – угол в горизонтальной плоскости, отсчитываемый от северного направления истинного меридиана по ходу часовой стрелки до данной линии (рис. 20). Истинный румб линии – острый горизонтальный угол, отсчитываемый от ближайшего направления истинного меридиана (северного или южного) до данной линии. 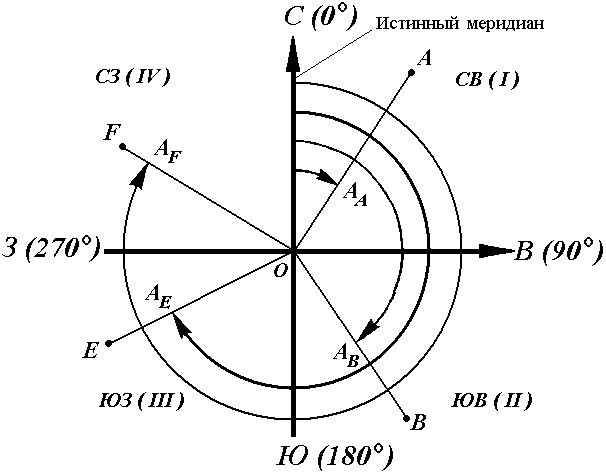 Рис. 20. Истинные азимуты Истинный азимут A измеряется от 0° до 360°. Зависимость между истинными азимутами и румбами такая же, как и между дирекционными углами и осевыми румбами. Истинные меридианы, проходящие через точки Земли с разной долготой, не параллельны между собой и сходятся на полюсах. Поэтому азимуты одной и той же прямой линии, определяемые относительно разных истинных меридианов, отличаются на величину γ (рис. 21), которую называют углом сближения меридианов. Его приближенное значение можно рассчитать по формулам: γ = 0,54 · l ·tgφ или γ = sinφ · Δλ, где l – длина прямой линии между точками (км); φ – средняя широта линии; Δλ – разность долгот. При l = 1 км и широте Хабаровска φ = 48°28' угол сближения меридианов γ = 0,6' = 36". 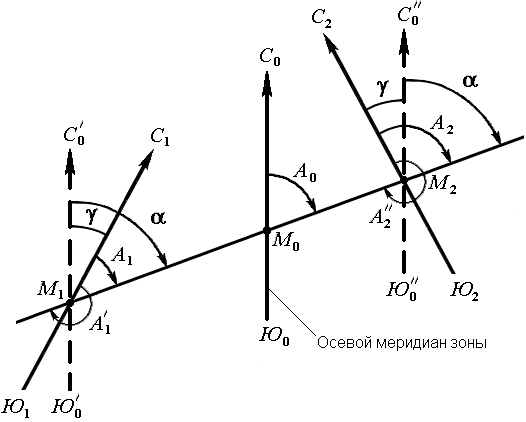 Рис. 21. Зависимость между истинным азимутом и дирекционным углом Рис. 21. Зависимость между истинным азимутом и дирекционным угломДля перехода от дирекционного угла к истинному азимуту и наоборот необходимо знать угол сближения γ между осевым и истинным меридианом (рис. 21). Зависимость между истинным азимутом и дирекционным углом следующая А = α + γ . Если точка расположена к западу от осевого меридиана, то величину угла сближения γ между осевым и истинным меридианом принято считать отрицательной, если к востоку – положительной (рис. 21). Например, истинные азимуты линии при дирекционном угле α = 70° и углах сближения γ = – 0°50' для западной точки М1, γ = 0°50' для восточной – М2 соответственно равны А1 = 70° – 0°50' = 69°50', А2 = 70° + 0°50' = 70°50'. Магнитные азимуты и румбы При ориентировании линий местности за основное направление может также приниматься направление магнитного меридиана. Магнитная стрелка на концах имеет точки, в которых сосредоточены магнитные массы. Соединяющая их линия называется магнитной осью стрелки. Вертикальная плоскость, проходящая через магнитную ось стрелки, является плоскостью магнитного меридиана. Линия пересечения плоскости магнитного меридиана с горизонтальной плоскостью дает направление магнитного меридиана. Горизонтальный угол, отсчитываемый от северного направления магнитного меридиана по ходу часовой стрелки до данной линии, называется магнитным азимутомАм (рис. 22). 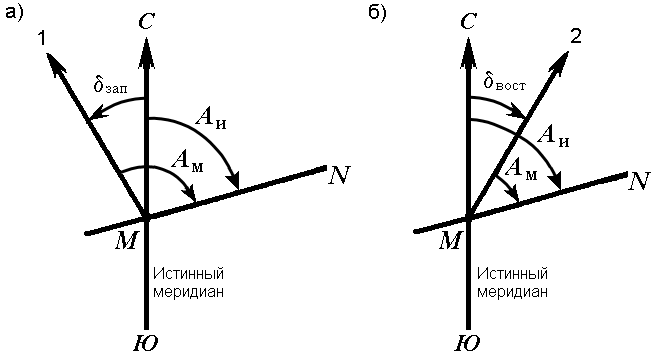 Рис. 22. Магнитный азимут и склонение магнитной стрелки: а) западное; б) восточное В каждой точке на поверхности Земли магнитный и истинный меридианы образуют между собой угол, называемый склонением магнитной стрелки δ (рис. 22). Северный конец магнитной стрелки может отклоняться от истинного меридиана к западу или востоку. В зависимости от этого различают западное и восточное склонения. Восточное склонение принято считать положительным, западное – отрицательным: Аи = Ам + δвост, Аи = Ам – δзап . Магнитное склонение в разных пунктах Земли различно и непостоянно. Различают вековые, годовые и суточные изменения склонения. В связи с этим магнитная стрелка указывает направление магнитного меридиана приблизительно и ориентировать линию по нему можно только тогда, когда не требуется большая точность ориентирования. Приборы для ориентирования на местности При ориентировании на местности для измерения магнитных азимутов и магнитных румбов пользуются буссолями (рис. 2.5, а) и компасами (рис. 2.5, б). Главные части буссоли или компаса - магнитная стрелка 1, вращающаяся на острие шпиля, и кольцо 2 с угловыми делениями. Северный конец стрелки делают темно-синим или вороненым. В зависимости от того, как подписаны деления, различают азимутальное и румбическое кольца. В азимутальном кольце деления подписывают против направления движения часовой стрелки от 0 до 360°, в румбическом - на концах нулевого диаметра ставят нули, перпендикулярного ему диаметра - 90°. В нерабочем состоянии стрелка приподнята на шпиле и прижата к защитному стеклу арретиром 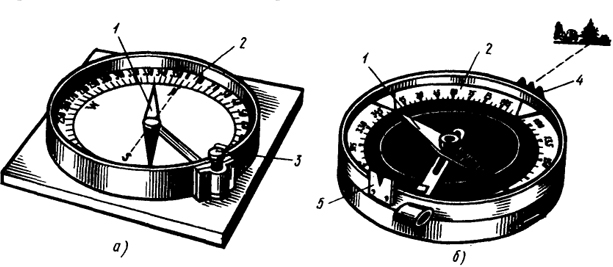 Рис. 2.5. Приборы для ориентирования по магнитным меридианам: а - буссоль, б - компас; 1 - стрелка, 2 - кольцо, 3 - арретир, 4, 5 - диоптры 3. Буссоли бывают штативные, устанавливаемые при измерениях на штатив; ручные, теодолитные, устанавливаемые на угломерные приборы - теодолиты; настольные, укладываемые на карту или план при их ориентировании. Настольная буссоль (рис. 2.5, а) называется ориентир-буссолью. Штативные, ручные буссоли и компасы имеют приспособление для визирования - наведения на точку линии, азимут которой измеряется. Простейшие виды таких приспособлений - диоптры: глазной 5 и предметный 4. В буссолях линия, соединяющая середины диоптров, постоянно совпадает с нулевым диаметром кольца; в компасах диоптры крепятся на вращающейся крышке. Принцип измерения азимута линии буссолью заключается в том, что нулевой диаметр буссоли совмещают с направлением этой линии, а по северному концу магнитной стрелки отсчитывают значение азимута или румба. Например, на рис. 2.5, а такой отсчет равен 335°5’. В компасе с подвижными диоптрами совмещают северный конец стрелки с нулем кольца, а линию диоптров - с направлением определяемой линии и по указателю предметного диоптра отсчитывают значение азимута данной линии. Для определения истинного азимута применяют гиротеодолит, сочетающий в себе гироскоп как датчик направления географического меридиана и измеритель углов - теодолит. Гироскоп представляет собой вращающееся устройство, подобное волчку, главная ось которого под действием суточного вращения Земли и силы тяжести всегда занимает положение, параллельное оси вращения Земли, т. е. в плоскости географического меридиана. Прямая геодезическая задача В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние SAB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол αAB или румб rAB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей. 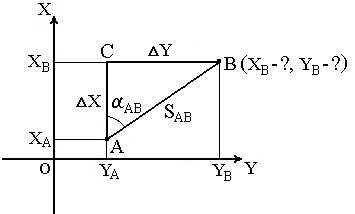 Рис. 23. Прямая геодезическая задача. Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом. Дано: Точка А( XA, YA ), SAB иαAB. Найти: точку В( XB, YB ). Непосредственно из рисунка имеем: ΔX = XB – XA; ΔY = YB – YA Разности ΔX и ΔY координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС: ΔX = SAB · cos αAB; ΔY = SAB · sin αAB. Так как в этих формулах SAB всегда число положительное, то знаки приращений координат ΔX и ΔY зависят от знаков cos αAB и sin αAB. Для различных значений углов знаки ΔX и ΔY представлены в табл.1. Таблица 1. Знаки приращений координат ΔX и ΔY
При помощи румба приращения координат вычисляют по формулам: ΔX = SAB · cosrAB; ΔY = SAB · sin rAB. Знаки приращениям дают в зависимости от названия румба. Вычислив приращения координат, находим искомые координаты другой точки: XB = XA + ΔX ; YB = YA+ ΔY. Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения. Обратная геодезическая задача Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA ) и В( XB, YB ) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB (рис.24). 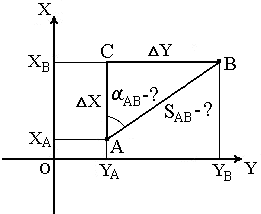 Рис. 24. Обратная геодезическая задача. Даннная задача решается следующим образом. Сначала находим приращения координат: ΔX = XB – XA; ΔY = YB – YA. Величину угла rAB определем из отношения
ΔX = сtgrАВ По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB. Для контроля расстояние SАВ дважды вычисляют по формулам: SАВ = ΔX/ cosαAB = ΔY/ sin αAB = ΔX · sec αАВ = ΔY · cosec αАВ Расстояние SАВ можно определить также по формуле Лекция 7. Угловые измерения Принцип измерения горизонтального угла 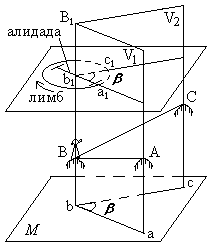 Углы обычно измеряют в градусной мере (градусы, минуты, секунды), реже - в радианной. За рубежом широко применяется градовая мера измерения углов (90 градусов – 100 градов). Углы обычно измеряют в градусной мере (градусы, минуты, секунды), реже - в радианной. За рубежом широко применяется градовая мера измерения углов (90 градусов – 100 градов).При геодезических работах измеряют не углы между сторонами на местности, а их ортогональные (горизонтальные) проекции, называемые горизонтальными углами. Так, для измерения угла АВС, стороны которого не лежат в одной плоскости, нужно предварительно спроектировать на горизонтальную плоскость точки А, В, и С (рис. 40) и измерить горизонтальный угол abc = β (рис.39). Рис. 40. Принцип измерения горизонтального угла Рассмотрим двугранный угол между вертикальными плоскостями V1 и V2 , проходящими через стороны угла АВС. Угол β для данного двугранного угла является линейным. Следовательно, углу β равен всякий другой линейный угол, вершина которого находится в любой точке на отвесном ребре ВВ1 двугранного угла, а стороны его лежат в плоскости, параллельной плоскости М. Итак, для измерения величины угла abc = β можно в любой точке, лежащей на ребре ВВ1 двугранного угла, допустим в точке b1, установить горизонтальный круг с градусными делениями и измерить на нем дугу a1c1, заключенную между сторонами двугранного угла, которая и будет градусной мерой угла a1b1c1, равной β , т.е. угол abc = β. Теодолит, его составные части Измерения горизонтальных проекций углов между линиями местности производят геодезическим угломерным прибором теодолитом. Для этого теодолит имеет горизонтальный угломерный круг с градусными делениями, называемый лимбом. Стороны угла проектируют на лимб с использованием подвижной визирной плоскости зрительной трубы. Она образуется визирной осью трубы при её вращении вокруг горизонтальной оси. Данную плоскость поочередно совмещают со сторонами угла ВА и ВС, последовательно направляя визирную ось зрительной трубы на точки А и С. При помощи специального отсчетного приспособления алидады, которая находится над лимбом соосно с ним и перемещается вместе с визирной плоскостью, на лимбе фиксируют начало и конец дуги a1c1 (см. рис. 40), беря отсчеты по градусным делениям. Разность взятых отсчетов является значением измеряемого угла β. Лимб и алидада, используемые для измерения горизонтальных углов, составляют в теодолите горизонтальный круг. Ось вращения алидады горизонтального круга называют основной осью теодолита. В теодолите также имеется вертикальный круг с лимбом и алидадой, служащий для измерения вертикальных проекций углов – углов наклона. Принято считать углы наклона выше горизонта положительными, а ниже горизонта – отрицательными. Лимб вертикального круга обычно наглухо скреплён со зрительной трубой и вращается вместе с ней вокруг горизонтальной оси теодолита. Перед измерением углов центр лимба с помощью отвеса или оптического центрира устанавливают на отвесной линии, проходящей через вершину измеряемого угла, а плоскость лимба приводят в горизонтальное положение, используя с этой целью три подъемных винта 3 и цилиндрический уровень 12 (рис. 41). В результате данных действий основная ось теодолита должна совпасть с отвесной линией, проходящей через вершину измеряемого угла. 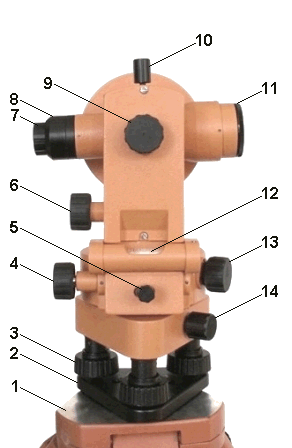  Рис. 41. Устройство теодолита 4Т30П 1 – головка штатива; 2 – основание; 3 – подъемный винт; 4 – наводящий винт алидады; 5 – закрепительный винт алидады; 6 – наводящий винт зрительной трубы; 7 – окуляр зрительной трубы; 8 – предохранительный колпачок сетки нитей зрительной трубы; 9 – кремальера; 10 – закрепительный винт зрительной трубы; 11 – объектив зрительной трубы; 12 – цилиндрический уровень; 13 – кнопочный винт для поворота лимба; 14 – закрепительный винт; 15 – окуляр отсчетного микроскопа с диоптрийным кольцом; 16 – зеркальце для подсветки штрихов отсчетного микроскопа; 17– колонка; 18 – ориентир-буссоль; 19 – вертикальный круг; 20 – визир; 21 – диоптрийное кольцо окуляра зрительной трубы; 22 – исправительные винты цилиндрического уровня; 23 – подставка. Для установки, настройки и наведения теодолита на цели в нем имеется система винтов: становой и подъемные винты, закрепительные (зажимные) и наводящие (микрометренные) винты, исправительные (юстировочные) винты. Становым винтом теодолит крепят к головке штатива, подъемными винтами – горизонтируют. Закрепительными винтами скрепляют подвижные части теодолита (лимб, алидаду, зрительную трубу) с неподвижными. Наводящими винтами сообщают малое и плавное вращение закрепленным частям. Чтобы теодолит обеспечивал получение неискаженных результатов измерений, он должен удовлетворять соответствующим геометрическим и оптико-механическим условиям. Действия, связанные с проверкой этих условий, называют поверками. Если какое-либо условие не соблюдается, с помощью исправительных винтов производят юстировку прибора. | ||||||||||||||||||||||
