Курс лекции по геодезии. Курс лекции по геодезии Акрам, руси. Лекция по дисциплине Геодезия Лекция Определение геодезии как науки и ее задачи. История геодезии
 Скачать 2.09 Mb.
|
|
Топографическое изучение земной поверхности заключается в определении положения ситуации и рельефа относительно математической поверхности Земли, т.е. в определении пространственных координат характерных точек, необходимых и достаточных для моделирования местности. Модель местности может быть представлена в виде геодезических чертежей, изготовление которых называют картографированием, и аналитически – в виде совокупности координат характерных точек. Для построения моделей местности в геодезии применяют метод проекций и различные системы координат. Метод горизонтальной проекции заключается в том, что изучаемые точки (A, B, C, D, E) местности с помощью вертикальных (отвесных) линии проектируются на уровенную поверхность У (рис. 5), в результате чего получают горизонтальные проекции этих точек (a, b, c, d, e). Отрезки Аa, Bb, Cc, Dd, Ee называются высотами точек, а качестве уровенной поверхности принимается геоид, и относительной или условной, если численные их значения – отметками. Высота точки 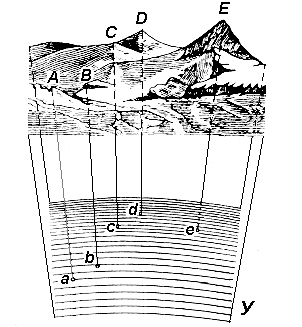 Рис. 5. Проектирование точек местности на уровенную поверхность Земли. является одной из её пространственных координат. Отметка называется абсолютной, если в для этого принимается произвольная уровенная поверхность.
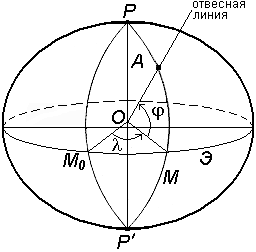
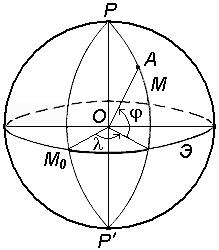
Две другие недостающие координаты точки определяются с помощью системы координат, построенной на математической поверхности Земли (рис. 6). Через любую точку поверхности референц-эллипсоида можно провести две взаимно перпендикулярные плоскости: плоскость геодезического меридиана – плоскость, проходящая через ось вращения Земли PP'; плоскость геодезической широты, которая перпендикулярна плоскости геодезического меридиана. Следы сечения поверхности референц-эллипсоида этими плоскостями называют меридианом (М) и параллелью. Меридиан, проходящий через астрономическую обсерваторию в Гринвиче, называется начальным или нулевым (М0). Параллель, плоскость которой проходит через центр Земли O, называется экватором (Э). Плоскость, проходящая через центр Земли O перпендикулярно к её оси вращения PP', называется экваториальной. Основой для всех систем координат являются плоскости меридиана и экватора. Системы координат подразделяются на угловые, линейные и линейно – угловые. Примером угловых координат являются географические координаты (рис.6): широта и долгота . Вдоль соответствующих параллели и меридиана широта и долгота точек постоянны. В геодезии применяются следующие системы координат: геодезические; астрономические; географические; плоские прямоугольные геодезические (зональные); полярные; местные. Геодезические координаты. Геодезические координаты определяют положение точки земной поверхности на референц-эллипсоиде (рис.7). Геодезическая широта B – угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью его экватора. Широта отсчитывается от экватора к северу или югу от 0° до 90° и соответственно называется северной или южной широтой. Геодезическая долгота L – двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического Гринвичского меридиана. Долготы точек, расположенных к востоку от начального меридиана, называются восточными, а к западу – западными. Астрономические координаты (для геодезии). Астрономическая широта и долгота определяют положение точки земной поверхности относительно экваториальной плоскости и плоскости начального астрономического меридиана (рис.8). Астрономическая широта – угол, образованный отвесной линией в данной точке и экваториальной плоскостью. Астрономическая долгота – двугранный угол между плоскостями астрономического меридиана данной точки и начального астрономического меридиана. Плоскостью астрономического меридиана является плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли. Астрономическая широта и долгота определяются астрономическими наблюдениями.
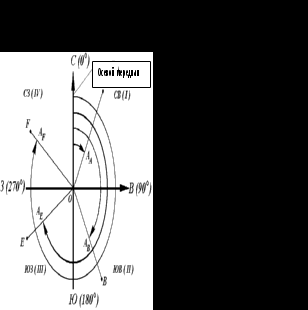
Геодезические и астрономические координаты отличаются (имеют расхождение) из-за отклонения отвесной линии от нормали к поверхности эллипсоида. При составлении географических карт этим отклонением пренебрегают. Географические координаты Географические координаты – величины, обобщающие две системы координат: геодезическую и астрономическую, используют в тех случаях, когда отклонение отвесных линий от нормали к поверхности не учитывается (рис.9). Географическая широта – угол, образованный отвесной линией в данной точке и экваториальной плоскостью. Географическая долгота – двугранный угол между плоскостями меридиана данной точки с плоскостью начального меридиана. Плоские прямоугольные геодезические координаты (зональные). При решении инженерно-геодезических задач в основном применяют плоскую прямоугольную геодезическую и полярную системы координат. Для определения положения точек в плоской прямоугольной геодезической системе координат используют горизонтальную координатную плоскость ХОУ (рис. 10), образованную двумя взаимно перпендикулярными прямыми. Одну из них принимают за ось абсцисс X, другую – за ось ординат Y, точку пересечения осей О – за начало координат. 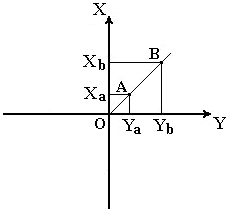 Рис. 10. Плоская прямоугольная система координат. Изучаемые точки проектируют с математической поверхности Земли на координатную плоскость ХОУ. Так как сферическая поверхность не может быть спроектирована на плоскость без искажений (без разрывов и складок), то при построении плоской проекции математической поверхности Земли принимается неизбежность данных искажений, но при этом их величины должным образом ограничивают. Для этого применяется равноугольная картографическая проекция Гаусса – Крюгера (проекция названа по имени немецких ученых, предложивших данную проекцию и разработавших формулы для её применения в геодезии), в которой математическая поверхность Земли проектируется на плоскость по участкам – зонам, на которые вся земная поверхность делится меридианами через 6° или 3°, начиная с начального меридиана (рис. 11). 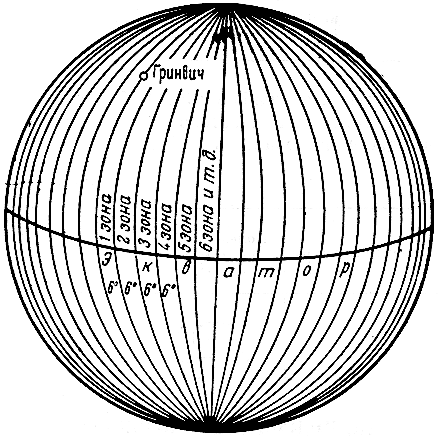 Рис. 11. Деление математической поверхности Земли на шестиградусные зоны В пределах каждой зоны строится своя прямоугольная система координат. С этой целью все точки данной зоны проецируются на поверхность цилиндра (рис. 12, а), ось которого находится в плоскости экватора Земли, а его поверхность касается поверхности Земли вдоль среднего меридиана зоны, называемого осевым. При этом соблюдается условие сохранения подобия фигур на земле и в проекции при малых рамерах этих фигур. 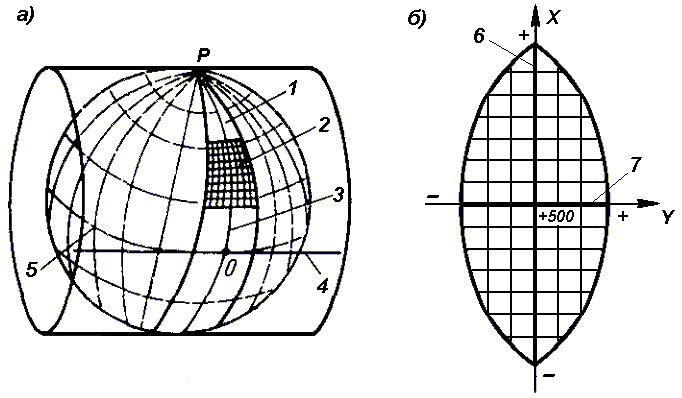 Рис. 12. Равноугольная картографическая проекция Гаусса – Крюгера (а) и зональная система координат (б):1 – зона, 2 – координатная сетка, 3 – осевой меридиан, 4 – проекция экватора на поверхность цилиндра, 5 – экватор,6 – ось абсцисс – проекция осевого меридиана, 7 – ось ординат – проекция экватора После проектирования точек зоны на цилиндр, он развертывается на плоскость, на которой изображение проекции осевого меридиана и соответствующего участка экватора будет представлена в виде двух взаимно перпендикулярных прямых (рис. 12, б). Точка пересечения их принимается за начало зональной плоской прямоугольной системы координат, изображение северного направления осевого меридиана – за положительную ось абсцисс, а изображение восточного направления экватора – за положительное направление оси ординат. Для всех точек на территории нашей страны абсциссы имеют положительное значение. Чтобы ординаты точек также были только положительными, в каждой зоне ординату начала координат принимают равной 500 км (рис. 12, б). Таким образом, точки, расположенные к западу от осевого меридиана, имеют ординаты меньше 500 км, а к востоку – больше 500 км. Эти ординаты называют преобразованными. На границах зон в пределах широт от 30° до 70° относительные ошибки, происходящие от искажения длин линий в этой проекции, колеблются от 1 : 1000 до 1 : 6000. Когда такие ошибки недопустимы, прибегают к трехградусным зонам. На картах, составленных в равноугольной картографической проекции Гаусса – Крюгера, искажения длин в различных точках проекции различны, но по разным направлениям, выходящим из одной и той же точки, эти искажения будут одинаковы. Круг весьма малого радиуса, взятый на уровенной поверхности, изобразится в этой проекции тоже кругом. Поэтому говорят, что рассматриваемая проекция конформна, т. е. сохраняет подобие фигур на сфере и в проекции при весьма малых размерах этих фигур. Таким образом, изображения контуров земной поверхности в этой проекции весьма близки к тем, которые получаются. Четверти прямоугольной системы координат нумеруются. Их счет идет по ходу стрелки от положительного направления оси абсцисс (рис.13). 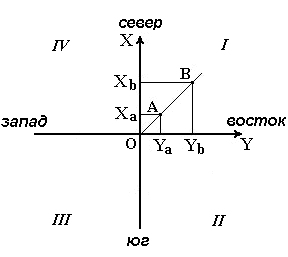 Рис. 13. Четверти прямоугольной системы координат. Если за начало плоской прямоугольной системы координат принять произвольную точку, то она будет называться относительной или условной. Полярные координаты При выполнении съемочных и разбивочных геодезических работ часто применяют полярную систему координат (рис.14). Она состоит из полюса О и полярной оси ОР, в качестве которых принимается прямая с известным началом и направлением. 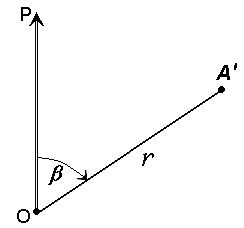 Рис. 14. Полярная система координат Для определения положения точек в данной системе используют линейно-угловые координаты: угол β, отсчитываемый по часовой стрелке от полярной оси ОР до направления на горизонтальную проекцию точки А', и полярное расстояние r от полюса системы О до проекции А'. Системы высот Высота точки является третьей координатой, определяющей её положение в пространстве. В геодезии для определения отметок точек применяются следующие системы высот (рис.15): ортометрическая (абсолютная); геодезическая; нормальная (обобщенная); относительная (условная). 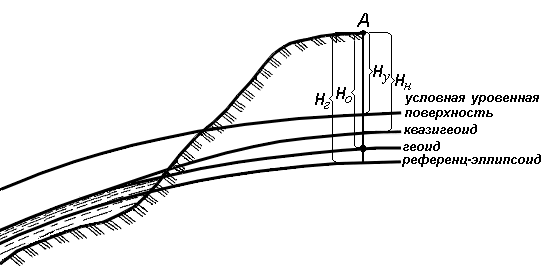 Рис. 15. Системы высот в геодезии Ортометрическая (абсолютная) высота ^ Hо – расстояние, отсчитываемое по направлению отвесной линии от поверхности геоида до данной точки. Геодезическая высота Hг– расстояние, отсчитываемое по направлению нормали от поверхности референц-эллипсоида до данной точки. В нашей стране все высоты реперов государственной нивелирной сети определены в нормальной системе высот. Это связано с тем, что положение геоида под материками определить сложно. Поэтому с конца 40-х годов в СССР было принято решение не применять ортометрическую систему высот В нормальной системе высот отметка точки Hн отсчитывается по направлению отвесной линии от поверхности квазигеоида, близкой к поверхности геоида. Квазигеоид («якобы геоид») – фигура, предложенная в 1950-х г.г. советским учёным М.С. Молоденским в качестве строгого решения задачи определения фигуры Земли. Квазигеоид определяется по измеренным значениям потенциалов силы тяжести согласно положениям теории М.С. Молоденского. В нашей стране все высоты реперов государственной нивелирной сети определены в нормальной системе высот. Это связано с тем, что положение геоида под материками определить сложно. Поэтому с конца 40-х годов в СССР было принято решение не применять ортометрическую систему высот. В России абсолютные высоты точек определяются в ^ Балтийской системе высот (БСВ) относительно нуля Кронштадтского футштока – горизонтальной черты на медной пластине, прикрепленной к устою моста через обводной канал в г. Кронштадте. Относительная высота Hу – измеряется от любой другой поверхности, а не от основной уровенной поверхности. Местная система высот – Тихоокеанская, её уровенная поверхность ниже нуля Кронштадтского футштока на 1873 мм. Лекция 6. Ориентирование линии. Прямая и обратная геодезические задачи. При выполнении геодезических работ на местности, а также при решении инженерно-геодезических задач на топографических картах и планах возникает необходимость в определении положения линий местности относительно какого-либо направления, принимаемого за основное (исходное). Такое определение называется ориентированием. Чаще всего за основное принимается направление меридиана, и положение линий местности определяется относительно сторон горизонта – севера, востока, юга и запада. Такое ориентирование называется ориентированием относительно стран света. В геодезии при ориентировании за основное направление принимают направление осевого, истинного или магнитного меридианов. При этом положение линии определяют с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута. Дирекционные углы и осевые румбы Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 16). Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°. 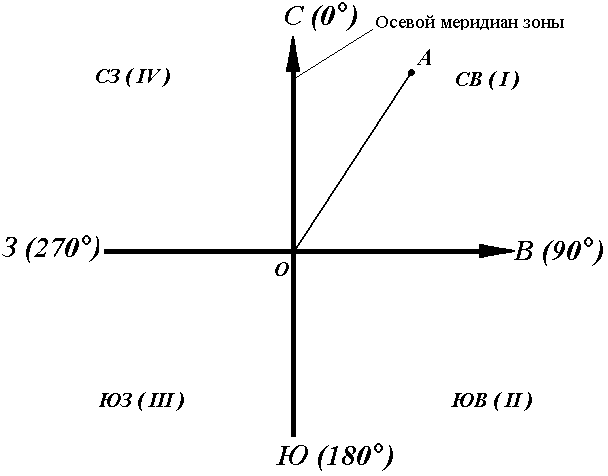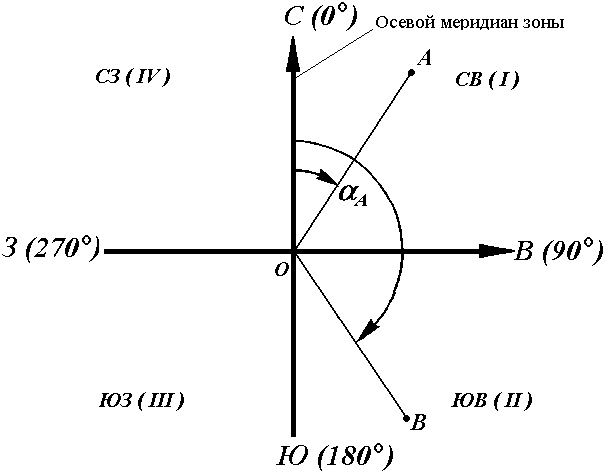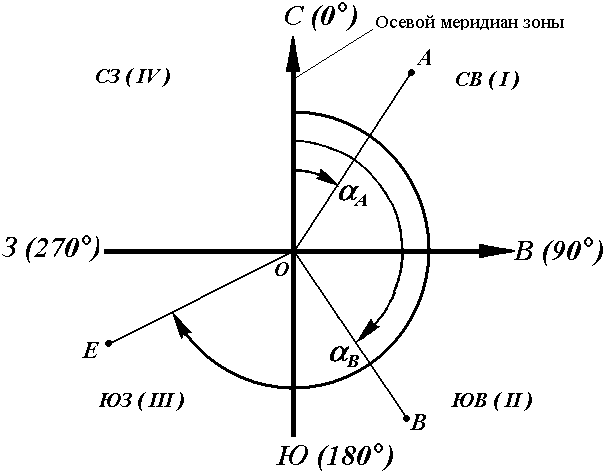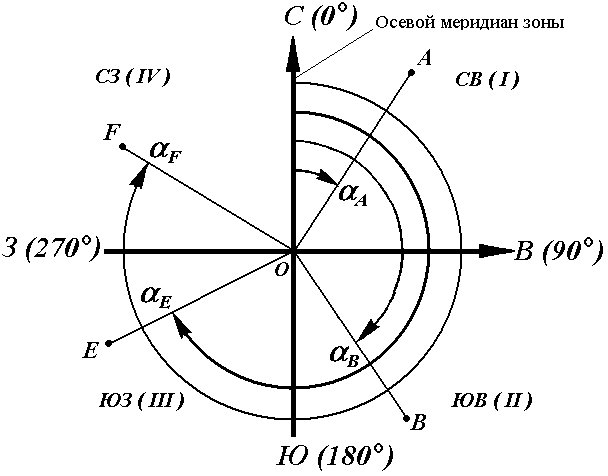 Рис. 16. Дирекционные углы. Для линии ОА её дирекционным углом в точке О является горизонтальный угол αОA между северным направлением осевого меридиана и направлением линии. Для линий ОВ, ОЕ и ОF – αОВ , αОE , αОF. Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии. В геодезии принято различать прямое и обратное направление линии (рис. 17). Так, если ^ ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим αBC является прямым дирекционным углом линии ВС в точке М, а угол αCB – обратным дирекционным углом этой же линии в той же точке. 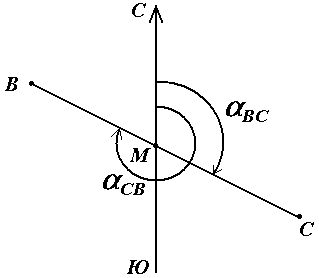 Рис. 17. Прямое и обратное направление линии Из рисунка видно, что αCB = αBC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°. Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 18). Осевым румбом называется острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб
I четверть (СВ) r = α II четверть (ЮВ) r = 180° – α III четверть (ЮЗ) r = α – 180° IV четверть (СЗ) r = 360° – α Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей. 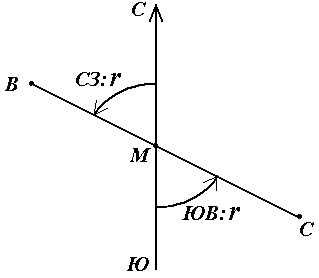 Рис. 19. Прямой и обратный румбы. |
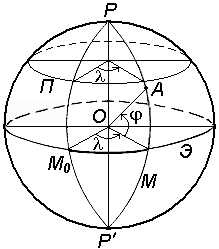
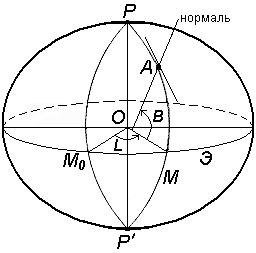Рис. 7. Система геодезических координат
