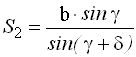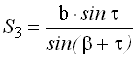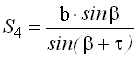Курс лекции по геодезии. Курс лекции по геодезии Акрам, руси. Лекция по дисциплине Геодезия Лекция Определение геодезии как науки и ее задачи. История геодезии
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
|
Приборы непосредственного измерения линий Для измерения длин линий посредством откладывания мерного прибора используют стальные мерные ленты, которые обычно изготавливают из ленточной углеродистой стали. В геодезической практике чаще всего применяются штриховые и шкаловые ленты. Штриховые ленты (рис. 47, а) имеют длину 20 и 24 м, ширину 15 – 20 мм и толщину 0,3 – 0,4 мм. 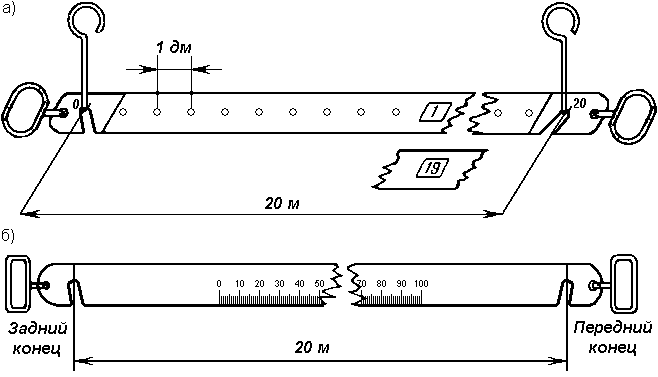 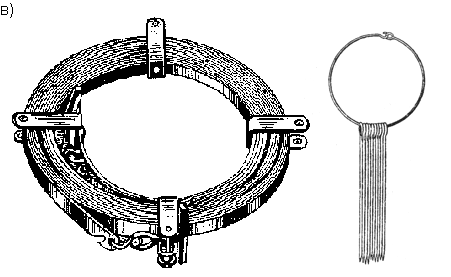 Рис. 1. Мерные ленты. На ленте нанесены метровые деления, обозначенные прикрепленными бляшками, и дециметровые деления, обозначенные отверстиями. Метровые деления на обеих сторонах оцифрованы. Счет оцифровки делений ведется на одной стороне от одного конца ленты, а на другом – от другого конца. За длину ленты принимают расстояние между штрихами, нанесенными на крюках у концов ленты. К крюкам приделаны ручки. К ленте прилагается 6 или 11 шпилек на кольце. Шпильки сделаны из стальной проволоки диаметром 5 – 6 мм и длиной 30 – 40 см в нерабочем положении ленту наматывают на кольцо (рис. 47, в). Шкаловая лента (рис.47, б) выпускается длиной 20 – 24 м, шириной 6 – 10 мм и толщиной 0,15 – 0, 20 мм. На обоих концах ленты, в пределах второго дециметра, имеются миллиметровые шкалы длиной по 100 мм каждая. Для измерения небольших расстояний применяют стальные и тесьмяные рулетки длиной 5, 10, 20, 50 м. Деления на рулетках нанесены на одной стороне через 1см и редко через 1 мм. Свернутая рулетка помещается в металлический или пластмассовый корпус. Компарирование мерных лент и рулеток Мерные ленты и рулетки перед измерением ими линий должны быть проверены. Данная проверка называется компарированием и состоит в установлении действительной длины мерного прибора путем его сравнения с образцовым прибором, длина которого точно известна. Для компарирования штриховых лент за образцовый мерный прибор принимают одну из лент, имеющихся на производстве, длину которой выверяют в лаборатории Государственного надзора за стандартами и измерительной техникой Государственного комитета стандартов РФ и пользуются ею при сравнении с рабочими лентами. Компарирование шкаловых лент производят на специальных приборах, называемых стационарными компараторами. Простейший способ компарирования штриховых лент состоит в следующем. На горизонтальной поверхности, например, на полу, укладывают образцовую ленту. Рядом с ней кладут проверяемую ленту так, чтобы их края касались друг друга, а нулевые штрихи совмещались. Жестко закрепив концы с нулевыми штрихами, ленты натягивают с одинаковой силой и измеряют миллиметровой линейкой величину несовпадения конечных штрихов на других концах лент. Данная величина показывает на сколько миллиметров рабочая лента короче или длиннее образцовой и называется поправкой за компарирование Δℓ. Длина проверяемой 20-метровой ленты не должна отличаться от длины образцовой ленты более чем на ±2 мм. В противном случае в результаты измерения линий вводят поправки. При этом, выполняя измерения линий рабочей лентой, полагают, что её длина равняется 20 м. Поправки определяют по формуле где D – длина измеренной линии. Поправку вычитают из результатов измерения, когда рабочая лента короче образцовой, и прибавляют, когда она длиннее. Прямую линию на местности обычно обозначают двумя вехами, установленными на её концах. Если длина линии превышает 100 м или на каких-то её участках не видны установленные вехи, то с целью удобства и повышения точности измерения её длины используют дополнительные вехи. Их устанавливают в воображаемой отвесной плоскости, проходящей через данную линию. Эту плоскость называют створом линии. Установка вех в створ данной линии называется вешением (рис. 48). 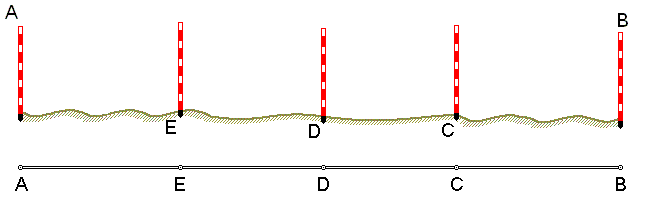 Рис. 48. Вешение линии Вешение линий может производиться на глаз, с помощью полевого бинокля или зрительной трубы прибора. Вешения обычно ведут «на себя». Наблюдатель становится на провешиваемой линии у вехи А (рис. 48), а рабочий по его указанию ставит веху в точку С так, чтобы она закрывала собой веху В. Таким же образом последовательно устанавливают вехи в точках D и Е. Установка вех в обратном направлении (от себя), является менее точной, так как ранее выставленные вехи закрывают видимость на последующие. Более точно вехи в створ выставляют по теодолиту, установленному в точке А и сориентированному на веху В. Порядок измерения линий штриховой лентой. Измерение линий на местности штриховыми лентами производят двое рабочих. По направлению измерения один из них считается задним, второй – передним. Ленту аккуратно разматывают с кольца. Её оцифровка должна возрастать по ходу измерения. Для закрепления мерной ленты в створе линии используется 6 шпилек. Перед началом измерения 5 шпилек берет передний мерщик и одну – задний. Задний мерщик совмещает с началом линии нулевой штрих ленты. Используя прорезь в ленте, закрепляет шпилькой её конец рядом с колышком, обозначающим начальную точку линии (рис. 49, а). Передний мерщик, имея в руке 5 шпилек, по указанию заднего мерщика, встряхнув ленту, натягивает её в створе линии и фиксирует первой шпилькой передний конец ленты. Затем задний мерщик вынимает свою шпильку из земли, вешает её на кольцо, и оба мерщика переносят ленту вперед вдоль линии. Дойдя до воткнутой в землю передним мерщиком шпильки, задний мерщик закрепляет на ней свой конец ленты, а передний, натянув ленту, закрепляет её передний конец следующей шпилькой (рис. 49, б). В таком порядке мерщики укладывают ленту в створе линии 5 раз. После того как передний мерщик зафиксирует пятой шпилькой свой конец ленты, задний мерщик передает ему кольцо с пятью шпильками, которые он собрал в процессе измерения (рис. 49, в). Число таких передач (т.е. отрезков по 100 м при длине ленты в 20 м) записывают в журнале измерений. Последний измеряемый остаток линии обычно меньше полной длины ленты. При определении его длины метры и дециметры отсчитывают по ленте, а сантиметры оценивают на глаз (рис. 49, е).  Рис. 49. Измерение линии мерной лентой Измеренная длина линии D вычисляется по формуле : D = 100 · a + 20 · b + c, где a – число передач шпилек; b – число шпилек у заднего мерщика на кольце; c – остаток. Для контроля линию измеряют вторично 24-метровой или той же 20-метровой в обратном направлении. За окончательный результат принимают среднее арифметическое из двух измерений, если их расхождение не превышает: – 1/3000 части от длины линии при благоприятных условиях измерений; – 1/2000 – средних условиях измерений; – 1/1000 – неблагоприятных условиях измерений. Вычисление горизонтальной проекции наклонной линии местности При создании планов местности вычисляют горизонтальную проекцию каждой линии, т.е. её горизонтальное проложение S. 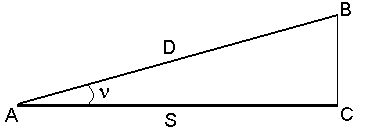 Рис. 50. Горизонтальная проекция линии Если линия АВ (рис. 50) наклонена к горизонту под углом ν, то определить горизонтальное проложение можно, воспользовавшись формулой где D – длина измеренной наклонной линии АВ; ν – угол наклона. Иногда для определения горизонтального проложения используют поправку за наклон тогда Поправку за наклон вводят при углах наклона более 1°. Углы наклона измеряют теодолитом. Косвенные измерения длин линий При измерении расстояний лентой или рулеткой встречаются случаи, когда местное препятствие (река, овраг, здание, дорога и т.п.) делает непосредственное измерение невозможным. Тогда применяют косвенные методы определения расстояний. Различают три случая определения недоступных расстояний. 1. При взаимной видимости точек разбивают базис b и измеряют горизонтальные углы 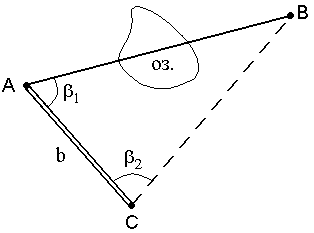 Рис. 51. Косвенное измерение расстояния через озеро Для определения расстояния АВ используют теорему синусов 2. При взаимной невидимости точек (рис. 52) выбирают точку С из которой видны точки А и В, измеряют расстояния S1, S2 и угол 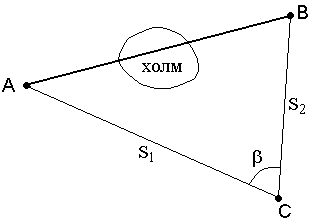 Рис. 52. Косвенное измерение расстояния через Используя теорему косинусов, находят расстояние АВ 3. Если обе точки измеряемого расстояния недоступны, то разбивают базис b и из точек С и Д измеряют углы 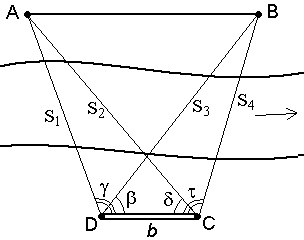 Рис. 53. Косвенное измерение расстояний если недоступны обе точки По теореме синусов дважды для контроля находят с контролем расстояние АВ.
Параллактический способ измерения расстояний Этот способ основан на решение треугольника АВС, в котором для определения расстояния SC высокой точностью измеряют перпендикулярную измеряемой линии малую сторону l, называемую базисом, и противолежащий ей острый параллактический ей острый параллактический угол 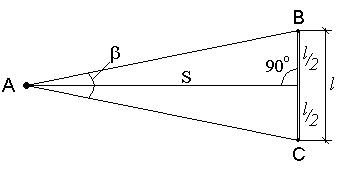 Рис. 54. Параллактический способ измерения расстояний. Измеряя расстояние этим способом, сразу получают горизонтальное проложение, поэтому введение поправок за наклон линии не требуется. Физико – оптические мерные приборы Второй способ измерения длин линий заключается в использовании физико-оптических приборов. Длину линии определяют как функцию угла, под которым виден базис (оптические дальномеры), или как функцию времени и скорости распространения электромагнитных волн между конечными точками измеряемой линии (электромагнитные дальномеры). Достоинством физико-оптических дальномеров является быстрота измерений, высокая точность и возможность измерения больших расстояний без подготовки трассы: нужна лишь оптическая видимость между конечными точками линии. Идея оптических дальномеров основана на решении параллактического треугольника, в котором по малому (параллактическому) углуβи противоположному ему катету (базе) B определяют расстояние D по формуле D = B ∙ ctg β 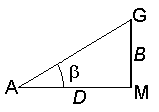 Рис. 55. Параллактический треугольник Одну из величин (В или β) принимают постоянной, а другую измеряют. В зависимости от этого различают оптические дальномеры с постоянной базой и переменным углом или с постоянным углом и переменной базой. Нитяный оптический дальномер Наиболее распространенным является нитяный дальномер с постоянным параллактическим углом. Он весьма прост по устройству и имеется в зрительных трубах всех геодезических приборов. Сетка нитей таких труб кроме основных вертикальной и горизонтальной нитей имеет дополнительные штрихи (нити), называемые дальномерными. С их помощью по дальномерной рейке определяют расстояние D между точками местности (рис. 56) 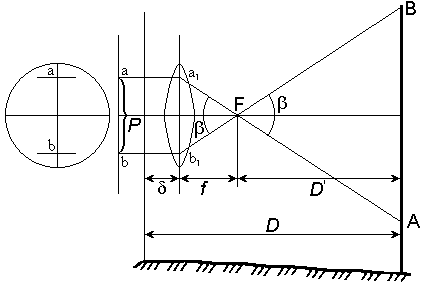 Рис. 56. Схема определения расстояний оптическим нитяным дальномером D = D' + f + δ где D' – расстояние от переднего фокуса объектива до рейки, f– фокусное расстояние объектива, δ- расстояние от оси вращения теодолита до объектива. Рассмотрим подобные треугольники АВF и а1b1F (рис. 56) ав /АВ = f /D' где аb = P – расстояние между дальномерными нитями, АВ = n – число сантиметровых делений между дальномерными нитями на рейке. Тогда D' = f /P ∙ n D = D' + f + δ = f /P ∙ n + f + δ Отношение f /P называется коэффициентом дальномера и обозначается K, а сумма (f +δ) – постоянная дальномера и обозначается С. Тогда D = K ∙ n + С. Дальномерные нити наносят так, чтобы при сантиметровых делениях коэффициент дальномера К = 100. Обычно при fобъектива равном 200 ммP берут равным 2 мм, тогда K = 100. В современных теодолитах постоянная дальномера С близка к нулю, поэтому число метров в измеряемом расстоянии равно числу метров в дальномерном отсчете D = K ∙ n = 100∙ n. При K = 100 и n = 124,3 см, D = 100 ∙ 124,3 см = 124,3 м. |