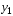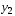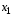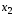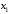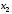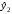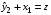Лекция по эконометрике. Лекция по эконометрике
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
|
Системы эконометрических уравнений 5.1 Общее понятие о системах уравнений, используемых в эконометрике Объектом статистического изучения в социальных науках являются сложные системы. Построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизма их функционирования. Поэтому при моделировании экономических ситуаций часто необходимо построение систем уравнений, когда одни и те же переменные могут выступать и в роли объясняющих и в роли объясняемых. Так, если изучается модель спроса как отношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением. Система уравнений в эконометрических исследованиях может быть построена по-разному. Системы уравнений здесь могут быть построены по-разному. Возможна система независимых уравнений, когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x: 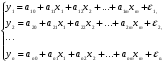 (1) (1)Набор факторов xj в каждом уравнении может варьироваться. Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется МНК. По существу, каждое уравнение этой системы является уравнением регрессии. Если зависимая переменная 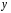 одного уравнения выступает в виде фактора одного уравнения выступает в виде фактора 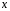 в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений: в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений: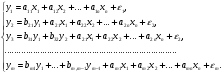 (2) (2)В данной системе зависимая переменная 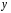 включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором факторов включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором факторов 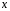 . Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК). . Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы: 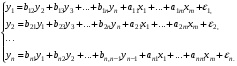 (3) (3)Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания. 5.2 Структурная и приведенная формы модели Экономическая модель как система одновременных уравнений может быть представлена в структурной или приведённой форме. В структурной форме её уравнения имеют исходный вид, отражая непосредственную связь между переменными. Структурная форма модели обычно содержит эндогенные и экзогенные переменные. Эндогенные переменные (внутренние) – это зависимые переменные, число которых равно числу уравнений в системе. Они обозначаются через y. Экзогенные переменные (внешние) – это предопределенные переменные (задаваемые извне, независимые), влияющие на эндогенные переменные. Они обозначаются через x. Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других – как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных можно рассматривать значения эндогенных переменных за предшествующий период времени (лаговые переменные). Например, потребление текущего года yt может зависеть также и от уровня потребления в предыдущем году yt-1. Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных. Простейшая структурная форма модели имеет вид: 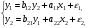 (4) (4)где y1,y2 – эндогенные переменные, x1,x2 – экзогенные. Коэффициенты 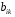 при эндогенных и при эндогенных и 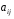 – при экзогенных переменных называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях – при экзогенных переменных называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях 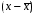 и и 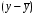 от среднего уровня, поэтому свободный член в каждом уравнении отсутствует. от среднего уровня, поэтому свободный член в каждом уравнении отсутствует.Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма преобразуется в приведенную. Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных: 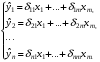 (5) (5)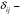 коэффициенты приведенной формы модели. коэффициенты приведенной формы модели.По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений. Применяя МНК, можно оценить 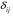 , а затем оценить значения эндогенных переменных через экзогенные. , а затем оценить значения эндогенных переменных через экзогенные.Коэффициенты приведённой формы представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели через коэффициенты структурной модели. Для структурной модели вида (4) приведенная форма модели имеет вид 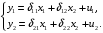 (6) (6)Из первого уравнения (4) можно выразить 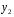 следующим образом (ради упрощения опускаем случайную величину): следующим образом (ради упрощения опускаем случайную величину):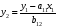 . .Подставляя во второе уравнение (4), имеем 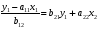 , ,Откуда 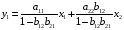 . .Аналогично выразим 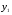 из второго уравнения системы (4) и подставив в первое, получим: из второго уравнения системы (4) и подставив в первое, получим: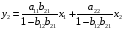 . .Т.о. система (4) принимает вид: 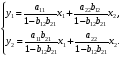 Таким образом, можно сделать вывод о том, что коэффициенты приведенной формы модели (6) будут выражаться через коэффициенты структурной формы следующим образом: 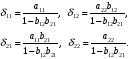 Следует заметить, что приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, но аналитически она уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными. 5.3 Проблема идентификации При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели. Структурная модель (3) в полном виде, состоящая в каждом уравнении системы из n эндогенных и m экзогенных переменных, содержит n(n-1+m) параметров. Приведенная модель (5) в полном виде содержит nm параметров. Таким образом, в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Поэтому n(n-1+m) параметров структурной модели не могут быть однозначно определены через nm параметров приведенной формы модели. Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели равны нулю. Тем самым уменьшится число структурных коэффициентов. С позиции идентифицируемости структурные модели можно подразделить на три вида: А) идентифицируемые; Б) неидентифицируемые; В) сверхидентифицируемые. А) Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т.е. число параметров структурной модели равно числу параметров приведенной формы модели. Б) Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель (3) в полном виде всегда неидентифицируема. В) Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе приведенных коэффициентов можно получить два или более значений одного структурного коэффициента. Сверхидентифицируемая модель, в отличие от неидентифицируемой, практически решаема, но требует для этого специальных методов исчисления параметров. Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение. Необходимое условие идентифицируемости (счётное правило проверки на идентифицируемость): Обозначим Н – число эндогенных переменных в i- ом уравнении системы, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Тогда: D+1 = Н – уравнение идентифицируемо; D+1 < Н – уравнение неидентифицируемо; D+1 > Н – уравнение сверхидентифицируемо. Это счетное правило отражает необходимое, но не достаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. Для оценки параметров структурной формы система должна быть идентифицируема или сверхидентифицируема. Пример. Проверить каждое уравнение системы на необходимое и достаточное условия идентификации: 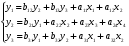 5.4 Оценивание параметров структурной модели Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение получили два метода оценивания коэффициентов структурной модели:
Косвенный и двухшаговый методы подробно описаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели. КМНК применяется для идентифицируемой системы одновременных уравнений, а ДМНК – для оценки коэффициентов сверхидентифируемой модели. Метод максимального правдоподобия с полной информацией рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т.Андерсоном и Н.Рубиным. В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. Несмотря на его значительную популярность, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего. Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК), предложенный в 1962 г. А.Зельнером и Г.Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК. Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы:
Рассмотрим применение КМНК для модели: 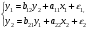 Пусть мы располагаем некоторыми данными по 5 регионам:
Приведенная форма модели имеет вид: 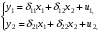 где 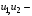 случайные ошибки приведенной формы модели. случайные ошибки приведенной формы модели.Для каждого уравнения приведенной формы применим традиционный МНК и определим δ- коэффициенты. Для простоты работаем в отклонениях, т.е. 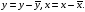 Тогда система нормальных уравнений для первого уравнения системы составит: Тогда система нормальных уравнений для первого уравнения системы составит: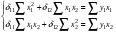 Для приведенных данных система составит: 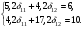 Отсюда получаем первое уравнение (и аналогично второе): 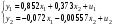 Перейдем к структурной форме следующим образом: исключим из первого уравнения приведенной формы x2 , выразив его из второго уравнения приведенной формы и подставив в первое уравнение: 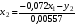 . .Первое уравнение структурной формы: 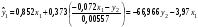 . .Аналогично исключим из второго уравнения x1, выразив его через первое уравнение и подставив во второе: 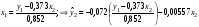 , ,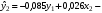 второе уравнение структурной формы. второе уравнение структурной формы.Структурная форма модели имеет вид: 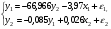 Эту же систему можно записать, включив в нее свободный член уравнения, т.е. перейти от переменных в виде отклонений от среднего к исходным переменным 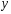 и и 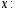 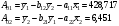 Тогда структурная модель имеет вид: 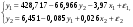 Если к каждому уравнению структурной формы применить традиционный МНК, то результаты могут сильно отличаться. В данном примере будет: 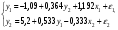 Двухшаговый МНК. ДМНК используется для сверхидентифицируемых систем. Основная идея ДМНК: на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Здесь дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной 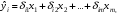 и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных. и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.Сверхидентифицируемая структурная модель может быть двух типов: - все уравнения системы сверхидентифицируемые; - система содержит также точно идентифицируемые уравнения. В первом случае для оценки структурных коэффициентов каждого уравнения используется ДМНК. Во втором случае структурные коэффициенты для точно идентифицируемых уравнений находятся из системы приведенных уравнений. ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК. Рассмотрим модель: 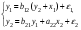 Она получена из предыдущего примера наложением ограничения 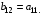 Поэтому первое уравнение стало сверхидентифицируемым. Поэтому первое уравнение стало сверхидентифицируемым.На первом шаге найдем приведенную форму модели. С использованием тех же исходных данных получим систему: 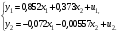 На основе второго уравнения этой системы можно найти теоретические значения для эндогенной переменной 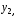 т.е. т.е. 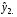 Подставим в это уравнение значения Подставим в это уравнение значения 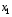 и и 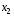 в форме отклонений от средних значений, запишем в виде таблицы: в форме отклонений от средних значений, запишем в виде таблицы:
После того, как найдены оценки 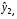 заменим в уравнении заменим в уравнении 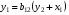 фактические значения фактические значения 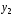 их оценками их оценками 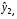 найдем значения новой переменной найдем значения новой переменной 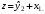 Применим МНК к уравнению: Применим МНК к уравнению: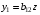 . .Получим: 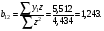 В целом рассматриваемая система будет иметь вид: 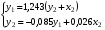 Второе уравнение не изменилось по сравнению с предыдущим примером. |

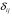 .
.