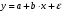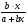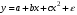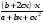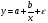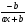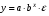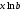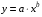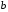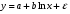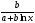Лекция по эконометрике. Лекция по эконометрике
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
|
3. Множественная корреляция и линейная регрессия Значения экономических переменных обычно определяется влиянием не одного, а нескольких факторов. Например, спрос на некоторое благо определяется не только ценой данного блага, но и ценами на замещающие и дополняющие блага, доходом потребителей и многими другими факторами. В этом случае вместо парной регрессии рассматривается множественная регрессия 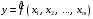 , где , где 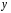 – зависимая переменная (результативный признак), – зависимая переменная (результативный признак), 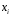 – независимые, или объясняющие, переменные (признаки-факторы). – независимые, или объясняющие, переменные (признаки-факторы).Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целом ряде других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. 3.1 Спецификация модели. Отбор факторов при построении уравнения множественной регрессии Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
Включение в модель факторов с высокой интеркорреляцией, может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором 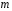 факторов, то для нее рассчитывается показатель детерминации факторов, то для нее рассчитывается показатель детерминации 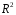 , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии 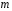 факторов. Влияние других, не учтенных в модели факторов, оценивается как факторов. Влияние других, не учтенных в модели факторов, оценивается как 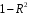 с соответствующей остаточной дисперсией с соответствующей остаточной дисперсией 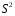 . .При дополнительном включении в регрессию 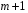 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться: фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться: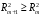 и и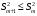 . .Если же этого не происходит и данные показатели практически не отличаются друг от друга, то включаемый в анализ фактор 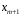 не улучшает модель и практически является лишним фактором. не улучшает модель и практически является лишним фактором.Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по критерию Стьюдента. Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии. Коэффициенты интеркорреляции позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 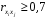 . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга. . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.Пусть, например, при изучении зависимости 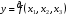 матрица парных коэффициентов корреляции оказалась следующей: матрица парных коэффициентов корреляции оказалась следующей:Таблица
Очевидно, что факторы 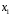 и и 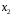 дублируют друг друга. В анализ целесообразно включить фактор дублируют друг друга. В анализ целесообразно включить фактор 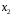 , а не , а не 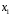 , хотя корреляция , хотя корреляция 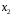 с результатом с результатом 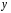 слабее, чем корреляция фактора слабее, чем корреляция фактора 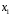 с с 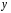 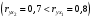 , но зато значительно слабее межфакторная корреляция , но зато значительно слабее межфакторная корреляция 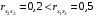 . Поэтому в данном случае в уравнение множественной регрессии включаются факторы . Поэтому в данном случае в уравнение множественной регрессии включаются факторы 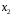 , , 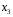 . .По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы 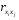 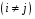 были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных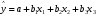 матрица коэффициентов корреляции между факторами имела бы определитель, равный единице: 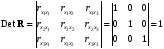 . .Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю: 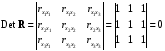 . .Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если 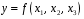 , то возможно построение следующего совмещенного уравнения: , то возможно построение следующего совмещенного уравнения: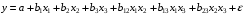 . .Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по 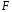 -критерию Фишера, но, как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми. -критерию Фишера, но, как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми.Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ. Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а 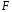 -критерий меньше табличного значения. -критерий меньше табличного значения.3.2 Метод наименьших квадратов (МНК) Возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. Задача оценки статистической взаимосвязи переменных формулируется аналогично случаю парной регрессии. Теоретическое уравнение множественной линейной регрессии имеет вид: 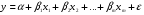 , ,где 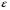 - случайная ошибка, - случайная ошибка, 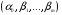 - вектор размерности - вектор размерности 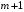 . .Для того, чтобы формально можно было решить задачу оценки параметров должно выполняться условие: объем выборки n должен быть не меньше количества параметров, т.е. 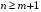 . .Если же это условие не выполняется, то можно найти бесконечно много различных коэффициентов. Если 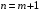 (например, 3 наблюдения и 2 объясняющие переменные), то оценки рассчитываются единственным образом без МНК путём решения системы: (например, 3 наблюдения и 2 объясняющие переменные), то оценки рассчитываются единственным образом без МНК путём решения системы: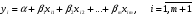 . .Если же 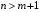 , то необходима оптимизация, т.е. выбрать наилучшую формулу зависимости. В этом случае разность , то необходима оптимизация, т.е. выбрать наилучшую формулу зависимости. В этом случае разность 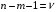 называется числом степеней свободы. Для получения надежных оценок параметров уравнения объём выборки должен значительно превышать количество определяемых по нему параметров. Практически, как было сказано ранее, объём выборки должен превышать количество параметров при xj в уравнении в 6-7 раз. называется числом степеней свободы. Для получения надежных оценок параметров уравнения объём выборки должен значительно превышать количество определяемых по нему параметров. Практически, как было сказано ранее, объём выборки должен превышать количество параметров при xj в уравнении в 6-7 раз.Задача построения множественной линейной регрессии состоит в определении 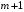 -мерного вектора -мерного вектора 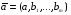 , элементы которого есть оценки соответствующих элементов вектора , элементы которого есть оценки соответствующих элементов вектора 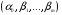 . .Уравнение с оценёнными параметрами имеет вид: 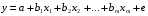 , ,где е – оценка отклонения ε. Параметры при 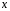 называются коэффициентами "чистой" регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне. называются коэффициентами "чистой" регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 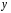 от расчетных от расчетных 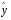 минимальна: минимальна: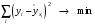 . .Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю. Итак, имеем функцию 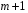 аргумента: аргумента: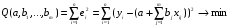 Она является квадратичной относительно неизвестных величин. Она ограничена снизу, следовательно имеет минимум. Находим частные производные первого порядка, приравниваем их к нулю, и получаем систему ( 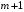 ) уравнения с ( ) уравнения с (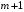 ) неизвестным. Обычно такая система имеет единственное решение. И называется системой нормальных уравнений: ) неизвестным. Обычно такая система имеет единственное решение. И называется системой нормальных уравнений: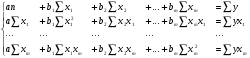 Решение может быть осуществлено методом Крамера: 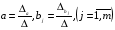 , где , где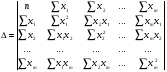 , ,а 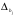 - частные определители, которые получаются из - частные определители, которые получаются из 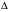 заменой соответствующего j – го столбца столбцом свободных членов. заменой соответствующего j – го столбца столбцом свободных членов.Для двухфакторной модели ( 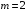 данная система будет иметь вид: данная система будет иметь вид: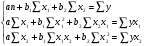 Матричный метод. Представим данные наблюдений и параметры модели в матричной форме. 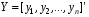 – n – мерный вектор – столбец наблюдений зависимой переменной; – n – мерный вектор – столбец наблюдений зависимой переменной;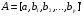 – (m+1) – мерный вектор – столбец параметров уравнения регрессии; – (m+1) – мерный вектор – столбец параметров уравнения регрессии;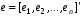 – n – мерный вектор – столбец отклонений выборочных значений yi от значений – n – мерный вектор – столбец отклонений выборочных значений yi от значений 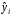 , получаемых по уравнению регрессии. , получаемых по уравнению регрессии.Для удобства записи столбцы записаны как строки и поэтому снабжены штрихом для обозначения операции транспонирования. Наконец, значения независимых переменных запишем в виде прямоугольной матрицы размерности 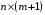 : :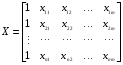 Каждому столбцу этой матрицы отвечает набор из n значений одного из факторов, а первый столбец состоит из единиц, которые соответствуют значениям переменной при свободном члене. В этих обозначениях эмпирическое уравнение регрессии выглядит так: 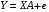 . .Где 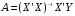 . .Здесь 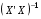 – матрица, обратная к – матрица, обратная к 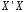 . .На основе линейного уравнения множественной регрессии 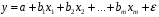 могут быть найдены частные уравнения регрессии: 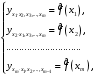 т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором 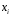 при закреплении остальных факторов на среднем уровне. В развернутом виде систему можно переписать в виде: при закреплении остальных факторов на среднем уровне. В развернутом виде систему можно переписать в виде: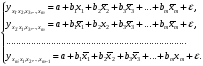 При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем 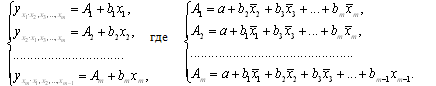 В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности: 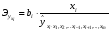 , ,где 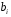 – коэффициент регрессии для фактора – коэффициент регрессии для фактора 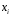 в уравнении множественной регрессии, в уравнении множественной регрессии,  – частное уравнение регрессии. – частное уравнение регрессии.Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности: 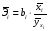 , которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. , которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.3.3 Анализ качества эмпирического уравнения множественной линейной регрессии Проверка статистического качества оцененного уравнения регрессии проводится, с одной стороны, по статистической значимости параметров уравнения, а с другой стороны, по общему качеству уравнения регрессии. Кроме этого, проверяется выполнимость предпосылок МНК. Как и в случае парной регрессии, для анализа статистической значимости параметров множественной линейной регрессии с m факторами, необходимо оценить дисперсию и стандартные отклонения параметров: Обозначим матрицу: 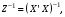 и в этой матрице обозначим j – й диагональный элемент как 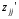 . Тогда выборочная дисперсия эмпирического параметра регрессии равна: . Тогда выборочная дисперсия эмпирического параметра регрессии равна: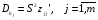 , ,а для свободного члена выражение имеет вид: 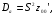 если считать, что в матрице 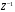 индексы изменяются от 0 до m. индексы изменяются от 0 до m.Здесь S2 – несмещенная оценка дисперсии случайной ошибки ε (среднеквадратическая ошибка регрессии): 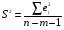 . .Соответственно, стандартные ошибки (отклонения) параметров 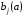 регрессии равны регрессии равны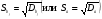 . .Для проверки значимости каждого коэффициента рассчитываются t – статистики: 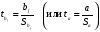 , ,Полученная t – статистика для соответствующего параметра имеет распределение Стьюдента с числом степеней свободы (n-т-1). При требуемом уровне значимости α эта статистика сравнивается с критической точкой распределения Стьюдента t(α; n-т-1) (двухсторонней). Если 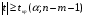 , то соответствующий параметр считается статистически значимым, и нуль – гипотеза в виде , то соответствующий параметр считается статистически значимым, и нуль – гипотеза в виде 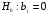 или или 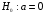 отвергается. отвергается.При 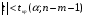 параметр считается статистически незначимым, и нуль – гипотеза не может быть отвергнута. Поскольку bj не отличается значимо от нуля, фактор хj линейно не связан с результатом. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Не оказывая какого–либо серьёзного влияния на зависимую переменную, он лишь искажает реальную картину взаимосвязи. Поэтому после установления того факта, что коэффициент bj статистически незначим, переменную хj рекомендуется исключить из уравнения регрессии. Это не приведет к существенной потере качества модели, но сделает её более конкретной. параметр считается статистически незначимым, и нуль – гипотеза не может быть отвергнута. Поскольку bj не отличается значимо от нуля, фактор хj линейно не связан с результатом. Его наличие среди объясняющих переменных не оправдано со статистической точки зрения. Не оказывая какого–либо серьёзного влияния на зависимую переменную, он лишь искажает реальную картину взаимосвязи. Поэтому после установления того факта, что коэффициент bj статистически незначим, переменную хj рекомендуется исключить из уравнения регрессии. Это не приведет к существенной потере качества модели, но сделает её более конкретной.Строгую проверку значимости параметров можно заменить простым сравнительным анализом. Если 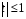 , т.е. , т.е. 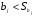 , то коэффициент статистически незначим. , то коэффициент статистически незначим.Если 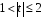 , т.е. , т.е. 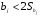 , то коэффициент относительно значим. В данном случае рекомендуется воспользоваться таблицей критических точек распределения Стьюдента. , то коэффициент относительно значим. В данном случае рекомендуется воспользоваться таблицей критических точек распределения Стьюдента.Если 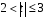 , то коэффициент значим. Это утверждение является гарантированным при (n-т-1)>20 и , то коэффициент значим. Это утверждение является гарантированным при (n-т-1)>20 и 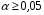 . .Если 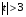 , то коэффициент считается сильно значимым. Вероятность ошибки в данном случае при достаточном числе наблюдений не превосходит 0,001. , то коэффициент считается сильно значимым. Вероятность ошибки в данном случае при достаточном числе наблюдений не превосходит 0,001.К анализу значимости коэффициента bj можно подойти по – другому. Для этого строится интервальная оценка соответствующего коэффициента. Если задать уровень значимости α, то доверительный интервал, в который с вероятностью (1-α) попадает неизвестное значение параметра 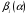 , определяется неравенством: , определяется неравенством: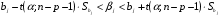 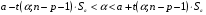 . .Если доверительный интервал не содержит нулевого значения, то соответствующий параметр является статистически значимым, в противном случае гипотезу о нулевом значении параметра отвергать нельзя. Для проверки общего качества уравнения регрессии используется коэффициент детерминации R2. Для множественной регрессии R2 является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение R2. Действительно, каждая следующая объясняющая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной. Анализ статистической значимости коэффициента детерминации проводится на основе проверки нуль-гипотезы Н0: R2=0 против альтернативной гипотезы Н1: R2>0. Для проверки данной гипотезы используется следующая F – статистика. Задача 1. Бюджетное обследование пяти случайно выбранных семей дало следующие результаты (в тыс. руб.):
А) Оценить регрессию S на Y и W. Б) Спрогнозируйте накопления семьи, имеющей доход 40 тыс.руб.и имущество стоимостью 25 тыс.руб. В) Предположим, что доход семьи вырос на 10 тыс.руб, в то время как стоимость имущества не изменилась. Оцените как возрастут её накопления. Г) Оцените как возрастут накопления семьи, если её доход вырос на 5, а стоимость имущетва увеличилась на 15. Задача 2. Для изучения жилья в городе по данным о 46 коттеджах было получено уравнение множественной регрессии: 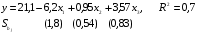 Где у – цена объекта (тыс.дол), 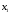 - расстояние до центра города, - расстояние до центра города, 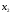 - полезная площадь объекта (кв.м), - полезная площадь объекта (кв.м), 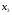 - число этажей в доме (ед.). - число этажей в доме (ед.).А) Проверить гипотезы о равенстве нулю коэффициентов 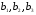 в генеральной совокупности (т.е. проверить значимость коэффициентов регрессии). в генеральной совокупности (т.е. проверить значимость коэффициентов регрессии).Б) Проверить гипотезу об одновременном равенстве нулю коэффициентов множественной регрессии (или о том, что R2=0) в ген.совокупности.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам. Например, – полиномы различных степеней – 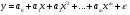 , , 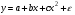 , , 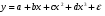 ; ;– равносторонняя гипербола – 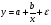 ; ;– полулогарифмическая функция – 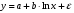 . .2. Регрессии, нелинейные по оцениваемым параметрам. Например, – степенная – 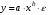 ; ;– показательная – 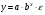 ; ;– экспоненциальная – 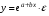 . .1. Регрессии нелинейные по включенным переменным сводятся к линейному виду с помощью методов линеаризации простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции. Полином второй степени 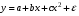 приводится к линейному виду с помощью замены: приводится к линейному виду с помощью замены: 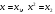 . В результате приходим к двухфакторному уравнению . В результате приходим к двухфакторному уравнению 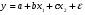 , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений: , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений: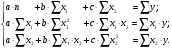 А после обратной замены переменных получим 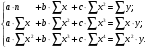 Полином второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. Аналогично, для полинома третьего порядка получим трёхфакторную модель. Для полинома степени m, получим множественную регрессию с m объясняющими переменными 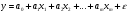 . .Среди нелинейной полиномиальной модели чаще всего используется полином второй степени, реже – третьей. Для равносторонней гиперболы 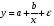 замена замена 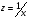 приводит к уравнению парной линейной регрессии приводит к уравнению парной линейной регрессии 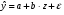 , для оценки параметров которого используется МНК. Система линейных уравнений при применении МНК будет выглядеть следующим образом: , для оценки параметров которого используется МНК. Система линейных уравнений при применении МНК будет выглядеть следующим образом: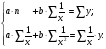 Такая модель может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы (например, кривая А.В. Филлипса), расходов на непродовольственные товары от доходов или общей суммы расходов (например, кривые Э. Энгеля) и в других случаях. Аналогичным образом приводятся к линейному виду зависимости 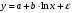 , , 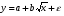 и другие. и другие.2. Регрессии, нелинейными по оцениваемым параметрам, делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся). К внутренне линейным моделям относятся, например, степенная функция – 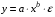 , показательная – , показательная – 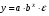 , экспоненциальная – , экспоненциальная – 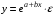 , логистическая – , логистическая – 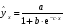 , обратная – , обратная – 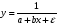 . Среди нелинейных моделей наиболее часто используется степенная функция . Среди нелинейных моделей наиболее часто используется степенная функция 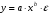 , которая приводится к линейному виду логарифмированием: , которая приводится к линейному виду логарифмированием: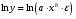 ; ;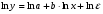 ; ;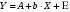 , ,где 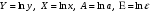 . Т.е. МНК мы применяем для преобразованных данных: . Т.е. МНК мы применяем для преобразованных данных: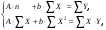 а затем потенцированием находим искомое уравнение. Широкое использование степенной функции связано с тем, что параметр 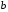 в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид: в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид: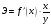 . .Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора 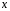 , то обычно рассчитывается средний коэффициент эластичности: , то обычно рассчитывается средний коэффициент эластичности: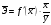 . .Наконец, следует отметить зависимость логистического типа: 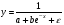 . Графиком функции является так называемая "кривая насыщения", которая имеет две горизонтальные асимптоты . Графиком функции является так называемая "кривая насыщения", которая имеет две горизонтальные асимптоты 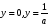 и точку перегиба и точку перегиба 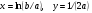 , а также точку пересечения с осью ординат , а также точку пересечения с осью ординат 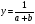 : :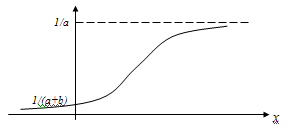 Уравнение приводится к линейному виду заменами переменных 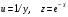 . .К внутренне нелинейным моделям можно, например, отнести следующие модели: 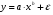 , , 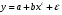 , , 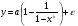 . .В случае, когда функция не поддаётся непосредственной линейной линеаризации, можно разложить её в функциональный ряд и затем оценить регрессию с членами этого ряда. При линеаризации функции или разложении её в ряд возникают и другие проблемы: искажение отклонений 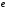 и нарушение их первоначальных свойств, статистическая зависимость членов ряда между собой. и нарушение их первоначальных свойств, статистическая зависимость членов ряда между собой.Например, если оценивается формула 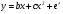 , полученная путём линеаризации или разложения в ряд, то независимые переменные , полученная путём линеаризации или разложения в ряд, то независимые переменные 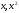 связаны между собой функционально. связаны между собой функционально.Поэтому во многих случаях актуальна непосредственная оценка нелинейной формулы регрессии. Для этого используется нелинейный МНК, идея которого основана на минимизации суммы квадратов отклонений расчётных значений от эмпирических, т.е. нужно оценить параметры вектора а функции 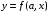 , так чтобы ошибки , так чтобы ошибки 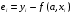 по совокупности были минимальны: по совокупности были минимальны: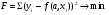 . .Для решения этой задачи существуют два пути: 1) непосредственная минимизация функции F с помощью методов нелинейной оптимизации, позволяющих находить экстремум выпуклых линий (метод наискорейшего спуска). 2) решение системы нелинейных уравнений, которая получается из необходимого условия экстремума функции – равенство нулю частных производных по каждому из параметров: 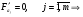 система уравнений: система уравнений: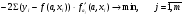 . .Эта система может быть решена итерационными методами. Однако в общем случае решение такой системы не является более простым способом нахождения вектора а. Существуют методы оценивания нелинейной регрессии, сочетающие непосредственную оптимизацию, использующую нахождение градиента, с разложением в ряд Тейлора для последующей оценки линейной регрессии (метод Марквардта). При построении нелинейной регрессии более остро, чем в линейном случае, стоит проблема правильной оценки формы зависимости между переменными. Неточности при выборе формы функции существенно сказываются на качестве отдельных параметров уравнения и соответственно, на адекватности всей модели в целом. Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции: 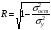 Здесь 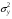 - общая дисперсия результативного признака y, - общая дисперсия результативного признака y, 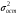 - остаточная дисперсия, определяемая по уравнению нелинейной регрессии - остаточная дисперсия, определяемая по уравнению нелинейной регрессии 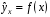 . Следует обратить внимание на то, что разности в соответствующих суммах . Следует обратить внимание на то, что разности в соответствующих суммах 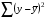 и и 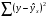 берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. По-другому можно записать так: берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. По-другому можно записать так: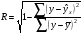 Величина R находится в границах 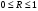 , и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. При этом индекс корреляции совпадает с линейным коэффициентом корреляции в случае, когда преобразование переменных с целью линеаризации уравнения регрессии не проводится с величинами результативного признака. Так обстоит дело с полулогарифмической и полиномиальной регрессией, а также с равносторонней гиперболой. Определив линейный коэффициент корреляции для линеаризованных уравнений, например, в пакете Excel с помощью функции ЛИНЕЙН, можно использовать его и для нелинейной зависимости. , и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. При этом индекс корреляции совпадает с линейным коэффициентом корреляции в случае, когда преобразование переменных с целью линеаризации уравнения регрессии не проводится с величинами результативного признака. Так обстоит дело с полулогарифмической и полиномиальной регрессией, а также с равносторонней гиперболой. Определив линейный коэффициент корреляции для линеаризованных уравнений, например, в пакете Excel с помощью функции ЛИНЕЙН, можно использовать его и для нелинейной зависимости.Иначе обстоит дело в случае, когда преобразование проводится также с величиной y, например, взятие обратной величины или логарифмирование. Тогда значение R, вычисленное той же функцией ЛИНЕЙН, будет относиться к линеаризованному уравнению регрессии, а не к исходному нелинейному уравнению, и величины разностей под суммами будут относиться к преобразованным величинам, а не к исходным, что не одно и то же. При этом, как было сказано выше, для расчета R следует воспользоваться выражением, вычисленным по исходному нелинейному уравнению. Поскольку в расчете индекса корреляции используется соотношение факторной и общей СКО, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации. Оценка существенности индекса корреляции проводится так же, как и оценка надежности коэффициента корреляции. Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера: 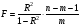 , ,где n-число наблюдений, m-число параметров при переменных х. Во всех рассмотренных нами случаях, кроме полиномиальной регрессии, m=1, для полиномов число параметров равно m, т.е. степени полинома. Величина m характеризует число степеней свободы для факторной СКО, а (n-m-1) – число степеней свободы для остаточной СКО. Индекс детерминации R2 можно сравнивать с коэффициентом детерминации r2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем больше разница между R2 и r2. Близость этих показателей означает, что усложнять форму уравнения регрессии не следует и можно использовать линейную функцию. Практически, если величина (R2-r2) не превышает 0,1, то линейная зависимость считается оправданной. В противном случае проводится оценка существенности различия показателей детерминации, вычисленных по одним и тем же данным, через t-критерий Стьюдента: 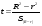 . .Здесь в знаменателе находится ошибка разности (R2-r2), определяемая по формуле: 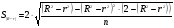 Если 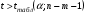 , то различия между показателями корреляции существенны и замена нелинейной регрессии линейной нецелесообразна. , то различия между показателями корреляции существенны и замена нелинейной регрессии линейной нецелесообразна.В заключение приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии:
|