|
|
Лекция по эконометрике. Лекция по эконометрике
Лекция по эконометрике
Введение
Эконометрика – наука, исследующая количественные закономерности и взаимозависимости в экономике на основе методов теории вероятностей и математической статистики, адаптированных к обработке экономических данных.
Основным элементом курса является анализ и построение взаимосвязей экономических переменных.
Математическая статистика и ее применение в экономике – эконометрика – позволяют строить экономические модели, оценивать их параметры, проверять гипотезы о свойствах экономических показателей и формах их связи, что в конечном счёте служит основой для экономического анализа и прогнозирования (основная цель эконометрики).
Экономические модели позволяют выявить особенности экономического объекта и на основе этого предсказывать будущее поведение объекта при изменении каких-либо параметров (повышение обменного курса, падение прибыли…).
По своему определению любая экономическая модель абстрактна и, следовательно, неполна. Так, например, в простейшей модели спроса предполагают, что спрос на какой-либо товар определяется его ценой (р) и доходом потребителя (I): 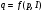 . .
На самом же деле на спрос влияют также другие факторы (цены на другие товары, реклама, мода, погода и т.д.). Поэтому в модель добавляют, обычно аддитивным образом, случайный компонент ε, интегрирующий (объединяющий) в себе влияние всех неучтённых явно в модели факторов. Например, модель спроса принимает вид: 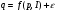 . .
Введение случайного компонента в модель приводит к тому, что взаимосвязь остальных её переменных перестаёт быть строго детерминированной (функциональной) и становится стохастической (статистической, случайной), каковая и наблюдается в реальной действительности.
Связь переменных, на которую накладываются воздействия случайных факторов, называется статистической (корреляционной).
Основой для выявления и обоснования эмпирических (опытных) закономерностей являются статистические данные, которые обычно подразделяются на 2 вида:
- перекрёстные данные – данные по какому-либо экономическому показателю, полученные для различных однотипных объектов (фирм, регионов). При этом либо все данные относятся к одному периоду времени, либо временная принадлежность несущественна.
- временные ряды – данные, характеризующие один объект, но в разные моменты времени.
Существуют различные методы сбора экономических данных: опрос, анкетирование, получение официальной стат.отчётности…
Собранные данные могут быть представлены в различной форме: в виде таблиц, диаграмм, графиков.
Далее подготовленные данные подставляются в теоретическую модель, представленную аналитически (в виде некоторого уравнения) или в графическом виде.
При этом возникает ряд проблем, важнейшими из которых являются проверка согласованности теоретической модели с опытными данными, оценка параметров модели и проверка предположений (гипотез), лежащих в основе модели.
Основные этапы эконометрического исследования:
0. Постановочный этап – постановка проблемы, целей моделирования, сбор данных, анализ их качества.
I. Спецификация модели – выбор вида формулы зависимости.
II. Параметризация – оценка значений параметров выбранной модели.
III. Верификация – проверка качества полученных параметров и самой модели в целом.
IV. Использование построенной модели для объяснения поведения экономических показателей и прогнозирования.
Основные типы моделей:
Экономико-математическая модель – это математическое описание какого-либо экономического процесса или объекта.
Математические модели, используемые в экономике, можно подразделить на классы по ряду признаков, относящихся к особенностям моделируемых объектов, цели моделирования и используемого инструментария.
- Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупнённые материальные и финансовые показатели (ВВП, потребление, инвестиции, занятость, процентную ставку…).
Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики, либо поведение отдельной такой составляющей в рыночной среде.
- Теоретические модели позволяют изучать общие свойства экономики и её характерных элементов дедукцией (от общего к частному) выводов из формальных предпосылок.
Прикладные модели оценивают параметры функционирования конкретного экономического объекта и позволяют сформулировать рекомендации для практических решений. К прикладным относятся прежде всего эконометрические модели, оперирующие числовыми значениями экономических переменных и позволяющие статистически значимо оценивать их на основе имеющихся наблюдений.
Особое место в рыночной экономике занимают равновесные модели, которые описывают такие состояния экономики, когда результирующая всех сил, стремящихся вывести их из этого состояния, равна 0.
- Статические модели описывают состояние экономического объекта в конкретный момент или период времени.
Динамические модели включают взаимосвязи переменных во времени.
- Детерминированные модели предполагают строгие функциональные связи между переменными.
Стохастические допускают наличие случайных воздействий на исследуемые показатели и используют инструментарий теории вероятностей и математической статистики для их описания.
Приведём 3 основных класса моделей, которые применяются для анализа и прогнозирования в эконометрике:
1. Модели временных рядов: модели тренда 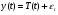 и сезонности и сезонности 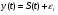 . Они объясняют поведение временного ряда, исходя только из его предыдущих значений. Применяются для изучения и прогнозирования объёма продаж билетов, спроса, прогнозирования % ставки. . Они объясняют поведение временного ряда, исходя только из его предыдущих значений. Применяются для изучения и прогнозирования объёма продаж билетов, спроса, прогнозирования % ставки.
2. Регрессионные модели с 1 уравнением: зависимая переменная у представляется в виде функции одной или нескольких переменных: 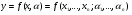 , где у – объясняемая (зависимая) переменная, , где у – объясняемая (зависимая) переменная, 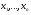 - объясняющие (независимые) переменные, - объясняющие (независимые) переменные, 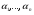 - параметры уравнения. - параметры уравнения.
Регрессионные уравнения – уравнения статистической связи между переменными.
В зависимости от вида функции f модели делятся на линейные и нелинейные. Эти модели применяют значительно шире, чем модели временных рядов. (Например, спрос на мороженое как функция от времени, температуры воздуха, среднего уровня доходов…).
3. Системы одновременных уравнений: описываются системами уравнений, могут состоять из тождеств и регрессионных уравнений, которые кроме объясняющих переменных могут включать в себя объясняемые переменные из других уравнений.
Линейная связь. Корреляция
Различные экономические явления как на микро-, так и на макроуровне не являются независимыми, а связаны между собой (цена товара и спрос на него, объём производства и прибыль фирмы и.т.д.).
Эта зависимость может быть строго функциональной (детермированной) и статистической.
Зависимость между 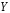 и и 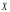 называется функциональной, когда каждому значению одного признака соответствует одно единственное значение другого признака. (Примером такой однозначной зависимости может служить зависимость площади круга от радиуса). называется функциональной, когда каждому значению одного признака соответствует одно единственное значение другого признака. (Примером такой однозначной зависимости может служить зависимость площади круга от радиуса).
В реальной действительности чаще встречается иная связь между явлениями, когда каждому значению одного признака могут соответствовать несколько значений другого (например, связь между возрастом детей и их ростом).
Форма связи, при которой один или несколько взаимосвязанных показателей (факторов) оказывают влияние на другой показатель (результат) не однозначно, а с определенной долей вероятности, называется статистической. В частности, если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическую зависимость называют корреляционной.
В зависимости от числа факторов, включаемых в модель, различают парную корреляцию (связь двух переменных) и множественную (зависимость результата от нескольких факторов).
Корреляционный анализ состоит в определении направления, формы и степени связи (тесноты) между двумя (несколькими) случайными признаками 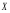 и и 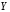 . .
По направлению корреляция бывает положительной (прямой), если при увеличении значений одной переменной увеличивается значение другой, и отрицательной (обратной), если при увеличении значений одной переменной, уменьшается значение другой.
По форме корреляционная связь может быть линейной (прямолинейной), когда изменение значений одного признака приводит к равномерному изменению другого (математически описывается уравнением прямой 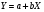 ), и криволинейной, когда изменение значений одного признака приводит к неодинаковым изменениям другого (математически она описывается уравнениями кривых линий, например гиперболы ), и криволинейной, когда изменение значений одного признака приводит к неодинаковым изменениям другого (математически она описывается уравнениями кривых линий, например гиперболы 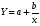 , параболы , параболы 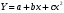 и т.д.). и т.д.).
Простейшей формой зависимости между переменными является линейная зависимость. И проверка наличия такой зависимости, оценивание её индикаторов и параметров является одним из важнейших направлений эконометрики.
Существуют специальные статистические методы и, соответственно, показатели, значения которых определённым образом свидетельствуют о наличии или отсутствии линейной связи между переменными.
1.1. Коэффициент линейной корреляции
Наиболее простым, приближенным способом выявления корреляционной связи является графический.
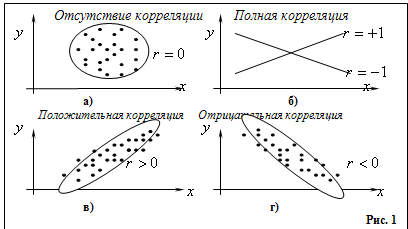
При небольшом объеме выборки экспериментальные данные представляют в виде двух рядов связанных между собой значений  и и 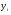 . Если каждую пару . Если каждую пару 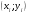 представить точкой на плоскости представить точкой на плоскости 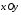 , то получится так называемое корреляционное поле (рис.1). , то получится так называемое корреляционное поле (рис.1).
Если корреляционное поле представляет собой эллипс, ось которого расположена слева направо и снизу вверх (рис.1в), то можно полагать, что между признаками существует линейная положительная связь.
Если корреляционное поле вытянуто вдоль оси слева направо и сверху вниз (рис.1г), то можно полагать наличие линейной отрицательной связи.
В случае же если точки наблюдений располагаются на плоскости хаотично, т.е корреляционное поле образует круг (рис.1а), то это свидетельствует об отсутствии связи между признаками.
На рис.1б представлена строгая линейная функциональная связь.
Под теснотой связи между двумя величинами понимают степень сопряженности между ними, которая обнаруживается с изменением изучаемых величин. Если каждому заданному значению 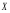 соответствуют близкие друг другу значения соответствуют близкие друг другу значения 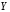 , то связь считается тесной (сильной); если же значения , то связь считается тесной (сильной); если же значения 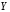 сильно разбросаны, то связь считается менее тесной. При тесной корреляционной связи корреляционное поле представляет собой более или менее сжатый эллипс. сильно разбросаны, то связь считается менее тесной. При тесной корреляционной связи корреляционное поле представляет собой более или менее сжатый эллипс.
Количественным критерием направления и тесноты линейной связи является коэффициент линейной корреляции.
Коэффициент корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции. Он вычисляется по формуле:

где 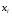 , , 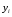 текущие значения признаков текущие значения признаков 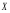 и и  ; ; 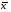 и и  средние арифметические значения признаков; средние арифметические значения признаков; 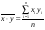 - среднее арифметическое произведений вариант, - среднее арифметическое произведений вариант, 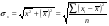 и и 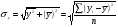 средние квадратические отклонения этих признаков; средние квадратические отклонения этих признаков;  объём выборки. объём выборки.
Для вычисления коэффициента корреляции достаточно принять предположение о линейной связи между случайными признаками. Тогда вычисленный коэффициент корреляции и будет мерой этой линейной связи.
Коэффициент линейной корреляции принимает значения от −1 в случае строгой линейной отрицательной связи, до +1 в случае строгой линейной положительной связи (т.е.  ). Близость коэффициента корреляции к 0 свидетельствует об отсутствии линейной связи между признаками, но не об отсутствии связи между ними вообще. ). Близость коэффициента корреляции к 0 свидетельствует об отсутствии линейной связи между признаками, но не об отсутствии связи между ними вообще.
Коэффициенту корреляции можно дать наглядную графическую интерпретацию.
Если 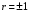 , то между признаками существует линейная функциональная зависимость вида , то между признаками существует линейная функциональная зависимость вида 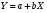 , что означает полную корреляцию признаков. При , что означает полную корреляцию признаков. При  , прямая имеет положительный наклон по отношению к оси , прямая имеет положительный наклон по отношению к оси  , при , при 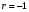 отрицательный (рис. 1б). отрицательный (рис. 1б).
Если 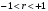 , точки , точки 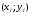 находятся в области ограниченной линией, напоминающей эллипс. Чем ближе коэффициент корреляции к находятся в области ограниченной линией, напоминающей эллипс. Чем ближе коэффициент корреляции к 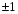 , тем уже эллипс и тем теснее точки сосредоточены вблизи прямой линии. При , тем уже эллипс и тем теснее точки сосредоточены вблизи прямой линии. При 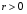 говорят о положительной корреляции. В этом случае значения говорят о положительной корреляции. В этом случае значения  имеют тенденцию к возрастанию с увеличением имеют тенденцию к возрастанию с увеличением 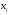 (рис.1в). При (рис.1в). При  говорят об отрицательной корреляции; значения говорят об отрицательной корреляции; значения 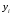 имеют тенденцию к уменьшению с ростом имеют тенденцию к уменьшению с ростом 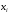 (рис.1г). (рис.1г).
Если 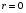 , то точки , то точки 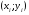 располагаются в области, ограниченной окружностью. Это означает, что между случайными признаками располагаются в области, ограниченной окружностью. Это означает, что между случайными признаками 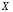 и и  отсутствует корреляция, и такие признаки называются некоррелированными (рис.1а). отсутствует корреляция, и такие признаки называются некоррелированными (рис.1а).
Также коэффициент линейной корреляции может быть близок (равен) нулю, когда между признаками есть связь, но она нелинейная (рис.2).

При оценке тесноты связи можно использовать следующую условную таблицу:
Теснота связи
|
Величина коэффициента корреляции при наличии
|
прямой связи (+)
|
обратной связи (−)
|
Связь отсутствует
|

|

|
Связь слабая
|

|
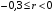
|
Связь умеренная
|
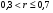
|
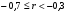
|
Связь сильная
|
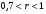
|
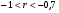
|
Полная функциональная
|
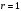
|
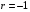
|
Заметим, что в числителе формулы для выборочного коэффициента линейной корреляции величин 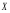 и и  с тоит их показатель ковариации: с тоит их показатель ковариации:
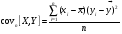
Этот показатель, как и коэффициент корреляции характеризует степень линейной связи величин 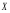 и и  . Если он больше нуля, то связь между величинами положительная, если меньше нуля, то связь – отрицательная, равен нулю – линейная связь отсутствует. . Если он больше нуля, то связь между величинами положительная, если меньше нуля, то связь – отрицательная, равен нулю – линейная связь отсутствует.
В отличие от коэффициента корреляции показатель ковариации нормирован – он имеет размерность, и его величина зависит от единиц измерения 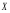 и и  . В статистическом анализе показатель ковариации обычно используется, как промежуточный элемент расчёта коэффициента линейной корреляции. Т.о. формула расчёта выборочного коэффициента корреляции приобретает вид: . В статистическом анализе показатель ковариации обычно используется, как промежуточный элемент расчёта коэффициента линейной корреляции. Т.о. формула расчёта выборочного коэффициента корреляции приобретает вид:
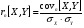
1.2 Оценка значимости (достоверности) коэффициента корреляции
Следует отметить, что истинным показателем степени линейной связи переменных является теоретический коэффициент корреляции, который рассчитывается на основании данных всей генеральной совокупности (т.е. всех возможных значений показателей):
 , ,
где  - теоретический показатель ковариции, который вычисляется как математическое ожидание произведений отклонений СВ - теоретический показатель ковариции, который вычисляется как математическое ожидание произведений отклонений СВ 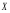 и и  от их математических ожиданий. от их математических ожиданий.
Как правило, теоретический коэффициент корреляции мы рассчитать не можем. Однако из того, что выборочный коэффициент не равен нулю 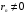 не следует, что теоретический коэффициент также не следует, что теоретический коэффициент также  (т.е. показатели могут быть линейно независимыми). Т.о. по данным случайной выборки нельзя утверждать, что связь между показателями существует. (т.е. показатели могут быть линейно независимыми). Т.о. по данным случайной выборки нельзя утверждать, что связь между показателями существует.
Выборочный коэффициент корреляции является оценкой теоретического коэффициента, т.к. он рассчитывается лишь для части значений переменных.
Всегда существует ошибка коэффициента корреляции. Эта ошибка - расхождение между коэффициентом корреляции выборки объемом 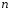 и коэффициентом корреляции для генеральной совокупности определяется формулами: и коэффициентом корреляции для генеральной совокупности определяется формулами:
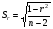
при 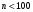 ; и ; и 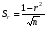 при при 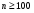 . .
Проверка значимости коэффициента линейной корреляции означает проверку того, насколько мы можем доверять выборочным данным.
С этой целью проверяется нулевая гипотеза 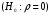 о том, что значение коэффициента корреляции для генеральной совокупности равно нулю, т.е. в генеральной совокупности отсутствует корреляция. Альтернативной является гипотеза о том, что значение коэффициента корреляции для генеральной совокупности равно нулю, т.е. в генеральной совокупности отсутствует корреляция. Альтернативной является гипотеза 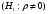 . .
Для проверки этой гипотезы рассчитывается 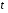 - статистика ( - статистика (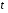 -критерий) Стьюдента: -критерий) Стьюдента:
 . .
Которая имеет распределение Стьюдента с 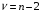 степенями свободы. По таблицам распределения Стьюдента определяется критическое значение степенями свободы. По таблицам распределения Стьюдента определяется критическое значение 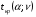 . Если рассчитанное значение критерия . Если рассчитанное значение критерия 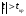 , то нуль-гипотеза отвергается, то есть вычисленный коэффициент корреляции значимо отличается от нуля с вероятностью , то нуль-гипотеза отвергается, то есть вычисленный коэффициент корреляции значимо отличается от нуля с вероятностью 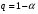 . .
Если же 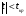 , тогда нулевая гипотеза не может быть отвергнута. В этом случае не исключается, что истинное значение коэффициента корреляции равно нулю, т.е. связь показателей можно считать статистически незначимой. , тогда нулевая гипотеза не может быть отвергнута. В этом случае не исключается, что истинное значение коэффициента корреляции равно нулю, т.е. связь показателей можно считать статистически незначимой.
Парная линейная регрессия. Метод наименьших квадратов
Коэффициент корреляции указывает на степень тесноты взаимосвязи между двумя признаками, но он не дает ответа на вопрос, как изменение одного признака на одну единицу его размерности влияет на изменение другого признака. Для того чтобы ответить на этот вопрос, пользуются методами регрессионного анализа.
Регрессионный анализ устанавливает форму зависимости между случайной величиной  и значениями переменной величины и значениями переменной величины  , причем, значения , причем, значения  считаются точно заданными. считаются точно заданными.
Уравнение регрессии – это формула статистической связи между переменными.
Если эта формула линейна, то речь идет о линейной регрессии. Формула статистической связи двух переменных называется парной регрессией (нескольких переменных – множественной).
Выбор формулы зависимости называется спецификацией уравнения регрессии. Оценка значений параметров выбранной формулы называется параметризацией.
Как же оценить значения параметров и проверить надёжность сделанных оценок?
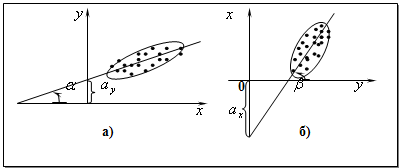
Рассмотрим рисунок
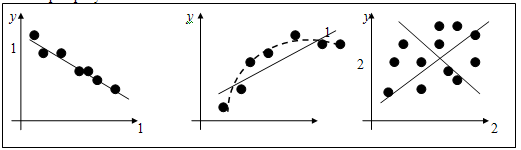
На графике (а) взаимосвязь х и у близка к линейной, прямая линия 1 здесь близка к точкам наблюдений и последние отклоняются от неё лишь в результате сравнительно небольших случайных воздействий.
На графике (б) реальная взаимосвязь величин х и у описывается нелинейной функцией 2, и какую бы мы ни провели прямую линию (например, 1), отклонения точек от неё будут неслучайными.
На графике (в) взаимосвязь между переменными х и у отсутствует, и результаты параметризации любой формулы зависимости будут неудачными.
Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Всегда можно попытаться провести такую прямую линию, которая будет "ближайшей" к точкам наблюдений по их совокупности (например, на рисунке (в) лучшей будет прямая 1, чем прямая 2).
Теоретическое уравнение парной линейной регрессии имеет вид:
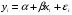 , ,
где  называются теоретическими параметрами (теоретическими коэффициентами) регрессии; называются теоретическими параметрами (теоретическими коэффициентами) регрессии; 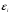 - случайным отклонением (случайной ошибкой). - случайным отклонением (случайной ошибкой).
В общем виде теоретическую модель будем представлять в виде:
 . .
Для определения значений теоретических коэффициентов регрессии необходимо знать все значения переменных Х и Y, т.е. всю генеральную совокупность, что практически невозможно.
Задача состоит в следующем: по имеющимся данным наблюдений 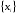 , , 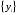 необходимо оценить значения параметров необходимо оценить значения параметров  . .
Пусть а – оценка параметра 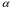 , b – оценка параметра , b – оценка параметра 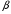 . .
Тогда оценённое уравнение регрессии имеет вид: , ,
где  теоретические значения зависимой переменной y, теоретические значения зависимой переменной y, 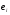 - наблюдаемые значения ошибок - наблюдаемые значения ошибок 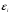 . Это уравнение называется эмпирическим уравнением регрессии. Будем его записывать в виде . Это уравнение называется эмпирическим уравнением регрессии. Будем его записывать в виде 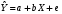 . .
В основе оценки параметров линейной регрессии лежит Метод Наименьших Квадратов (МНК) – это метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции.
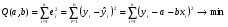 . .
Функция Q является квадратичной функцией двух параметров a и b. Т.к. она непрерывна, выпукла и ограничена снизу ( ), поэтому она достигает минимума. Необходимым условием существования минимума является равенство нулю её частных производных по a и b: ), поэтому она достигает минимума. Необходимым условием существования минимума является равенство нулю её частных производных по a и b:
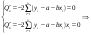 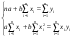 . .
Разделив оба уравнения системы на n, получим:
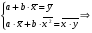 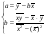 или или 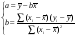
Иначе можно записать:
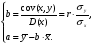
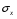 и и 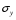 средние квадратические отклонения значений тех же признаков. средние квадратические отклонения значений тех же признаков.
Т.о. линия регрессии проходит через точку со средними значениями х и у 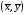 , а коэффициент регрессии b пропорционален показателю ковариации и коэффициенту линейной корреляции. , а коэффициент регрессии b пропорционален показателю ковариации и коэффициенту линейной корреляции.
Если кроме регрессии Y на X для тех же эмпирических значений найдено уравнение регрессии X на Y (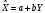 , где , где 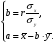 ), то произведение коэффициентов ), то произведение коэффициентов  : :
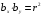 . .
Коэффициент регрессии  это величина, показывающая, на сколько единиц размерности изменится величина это величина, показывающая, на сколько единиц размерности изменится величина 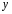 при изменении величины при изменении величины  на одну единицу ее размерности. Аналогично определяется коэффициент на одну единицу ее размерности. Аналогично определяется коэффициент  . .
Как и коэффициент корреляции, коэффициент регрессии может принимать и положительные и отрицательные значения. Например, если коэффициент  имеет знак "", то это означает, что при увеличении значения признака имеет знак "", то это означает, что при увеличении значения признака  на единицу его размерности значение признака на единицу его размерности значение признака  уменьшается на величину, равную уменьшается на величину, равную  . .
Уравнения линейной регрессии являются уравнениями прямых линий в плоскости 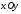 , проходящих внутри соответствующего корреляционного поля. Такие линии называются линиями регрессии. , проходящих внутри соответствующего корреляционного поля. Такие линии называются линиями регрессии.
Для того, чтобы полученные МНК оценки обладали желательными свойствами, сделаем следующие предпосылки об отклонениях 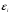 : :
1) величина 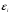 является случайной переменной; является случайной переменной;
2) математическое ожидание 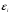 равно нулю: равно нулю: 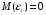 ; ;
3) значения 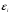 независимы между собой. Откуда вытекает, в частности, что независимы между собой. Откуда вытекает, в частности, что 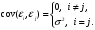
4) дисперсия 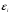 постоянна: постоянна: 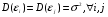 ; ;
5) ошибки 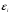 подчиняются нормальному распределению подчиняются нормальному распределению  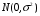 (это условие не является обязательным, но оно необходимо для проверки статистической значимости найденных оценок и определения для них доверительных интервалов). (это условие не является обязательным, но оно необходимо для проверки статистической значимости найденных оценок и определения для них доверительных интервалов).
Если условия 1)-4) выполняются, то оценки, сделанные с помощью МНК, обладают следующими свойствами:
1. Оценки являются несмещёнными (т.е. математическое ожидание каждого параметра равно его истинному значению  ). ).
2. Оценки состоятельны (дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю:  ). Иначе говоря, надёжность оценки при возрастании выборки растёт. Если n велико, то почти наверняка a близко к ). Иначе говоря, надёжность оценки при возрастании выборки растёт. Если n велико, то почти наверняка a близко к 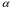 , а b близко к , а b близко к 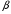 . .
3. Оценки эффективны, они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра, линейными относительно величин  . .
2. Оценка качества полученного уравнения (верификация)
Расчёт значений параметров уравнения регрессии – лишь первый шаг на пути решения проблемы количественного оценивания зависимости одной переменной от другой (других) переменных.
Следующим этапом решения этой проблемы является оценка качества построенного уравнения, вынесения суждения относительно его отдельных параметров и степени пригодности в целом.
Анализ качества оценённой зависимости включает статистическую и содержательную составляющие. Проверка статистического качества состоит из следующих элементов:
1. Проверка общего качества.
2. Проверка статистической значимости каждого коэффициента уравнения регрессии и всего уравнения в целом.
3. Проверка предпосылок, лежащих в основе МНК.
Под содержательной составляющей анализа качества понимается рассмотрение экономического смысла оценённого уравнения регрессии: действительно ли значимыми оказались объясняющие факторы, важные с точки зрения теории; положительны или отрицательны коэффициенты, показывающие направление действия этих факторов; попали ли оценки коэффициентов регрессии в предполагаемые из теоретических соображений интервалы. |
|
|
 Скачать 1.32 Mb.
Скачать 1.32 Mb.


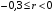
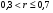
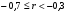
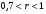
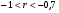
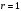
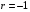
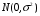 (это условие не является обязательным, но оно необходимо для проверки статистической значимости найденных оценок и определения для них доверительных интервалов).
(это условие не является обязательным, но оно необходимо для проверки статистической значимости найденных оценок и определения для них доверительных интервалов). ).
). ). Иначе говоря, надёжность оценки при возрастании выборки растёт. Если n велико, то почти наверняка a близко к
). Иначе говоря, надёжность оценки при возрастании выборки растёт. Если n велико, то почти наверняка a близко к 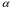 , а b близко к
, а b близко к 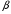 .
. .
.
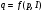 .
.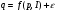 .
.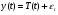 и сезонности
и сезонности 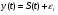 . Они объясняют поведение временного ряда, исходя только из его предыдущих значений. Применяются для изучения и прогнозирования объёма продаж билетов, спроса, прогнозирования % ставки.
. Они объясняют поведение временного ряда, исходя только из его предыдущих значений. Применяются для изучения и прогнозирования объёма продаж билетов, спроса, прогнозирования % ставки.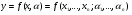 , где у – объясняемая (зависимая) переменная,
, где у – объясняемая (зависимая) переменная, 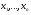 - объясняющие (независимые) переменные,
- объясняющие (независимые) переменные, 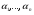 - параметры уравнения.
- параметры уравнения.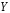 и
и 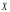 называется функциональной, когда каждому значению одного признака соответствует одно единственное значение другого признака. (Примером такой однозначной зависимости может служить зависимость площади круга от радиуса).
называется функциональной, когда каждому значению одного признака соответствует одно единственное значение другого признака. (Примером такой однозначной зависимости может служить зависимость площади круга от радиуса).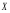 и
и 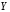 .
.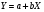 ), и криволинейной, когда изменение значений одного признака приводит к неодинаковым изменениям другого (математически она описывается уравнениями кривых линий, например гиперболы
), и криволинейной, когда изменение значений одного признака приводит к неодинаковым изменениям другого (математически она описывается уравнениями кривых линий, например гиперболы 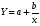 , параболы
, параболы 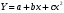 и т.д.).
и т.д.). и
и 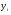 . Если каждую пару
. Если каждую пару 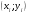 представить точкой на плоскости
представить точкой на плоскости 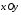 , то получится так называемое корреляционное поле (рис.1).
, то получится так называемое корреляционное поле (рис.1).
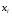 ,
, 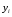 текущие значения признаков
текущие значения признаков  ;
; 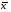 и
и  средние арифметические значения признаков;
средние арифметические значения признаков; 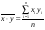 - среднее арифметическое произведений вариант,
- среднее арифметическое произведений вариант, 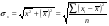 и
и 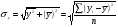 средние квадратические отклонения этих признаков;
средние квадратические отклонения этих признаков;  объём выборки.
объём выборки.
 ). Близость коэффициента корреляции к 0 свидетельствует об отсутствии линейной связи между признаками, но не об отсутствии связи между ними вообще.
). Близость коэффициента корреляции к 0 свидетельствует об отсутствии линейной связи между признаками, но не об отсутствии связи между ними вообще.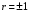 , то между признаками существует линейная функциональная зависимость вида
, то между признаками существует линейная функциональная зависимость вида 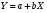 , что означает полную корреляцию признаков. При
, что означает полную корреляцию признаков. При  , прямая имеет положительный наклон по отношению к оси
, прямая имеет положительный наклон по отношению к оси  , при
, при 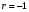 отрицательный (рис. 1б).
отрицательный (рис. 1б).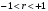 , точки
, точки 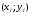 находятся в области ограниченной линией, напоминающей эллипс. Чем ближе коэффициент корреляции к
находятся в области ограниченной линией, напоминающей эллипс. Чем ближе коэффициент корреляции к 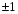 , тем уже эллипс и тем теснее точки сосредоточены вблизи прямой линии. При
, тем уже эллипс и тем теснее точки сосредоточены вблизи прямой линии. При 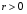 говорят о положительной корреляции. В этом случае значения
говорят о положительной корреляции. В этом случае значения  имеют тенденцию к возрастанию с увеличением
имеют тенденцию к возрастанию с увеличением 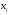 (рис.1в). При
(рис.1в). При  говорят об отрицательной корреляции; значения
говорят об отрицательной корреляции; значения 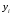 имеют тенденцию к уменьшению с ростом
имеют тенденцию к уменьшению с ростом 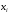 (рис.1г).
(рис.1г).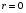 , то точки
, то точки 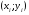 располагаются в области, ограниченной окружностью. Это означает, что между случайными признаками
располагаются в области, ограниченной окружностью. Это означает, что между случайными признаками 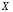 и
и 
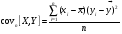
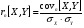
 ,
, - теоретический показатель ковариции, который вычисляется как математическое ожидание произведений отклонений СВ
- теоретический показатель ковариции, который вычисляется как математическое ожидание произведений отклонений СВ 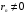 не следует, что теоретический коэффициент также
не следует, что теоретический коэффициент также  (т.е. показатели могут быть линейно независимыми). Т.о. по данным случайной выборки нельзя утверждать, что связь между показателями существует.
(т.е. показатели могут быть линейно независимыми). Т.о. по данным случайной выборки нельзя утверждать, что связь между показателями существует.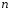 и коэффициентом корреляции для генеральной совокупности определяется формулами:
и коэффициентом корреляции для генеральной совокупности определяется формулами: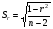
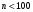 ; и
; и 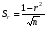 при
при 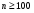 .
.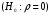 о том, что значение коэффициента корреляции для генеральной совокупности равно нулю, т.е. в генеральной совокупности отсутствует корреляция. Альтернативной является гипотеза
о том, что значение коэффициента корреляции для генеральной совокупности равно нулю, т.е. в генеральной совокупности отсутствует корреляция. Альтернативной является гипотеза 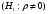 .
.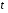 - статистика (
- статистика ( .
.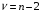 степенями свободы. По таблицам распределения Стьюдента определяется критическое значение
степенями свободы. По таблицам распределения Стьюдента определяется критическое значение 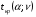 . Если рассчитанное значение критерия
. Если рассчитанное значение критерия 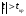 , то нуль-гипотеза отвергается, то есть вычисленный коэффициент корреляции значимо отличается от нуля с вероятностью
, то нуль-гипотеза отвергается, то есть вычисленный коэффициент корреляции значимо отличается от нуля с вероятностью 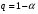 .
.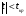 , тогда нулевая гипотеза не может быть отвергнута. В этом случае не исключается, что истинное значение коэффициента корреляции равно нулю, т.е. связь показателей можно считать статистически незначимой.
, тогда нулевая гипотеза не может быть отвергнута. В этом случае не исключается, что истинное значение коэффициента корреляции равно нулю, т.е. связь показателей можно считать статистически незначимой. и значениями переменной величины
и значениями переменной величины  , причем, значения
, причем, значения 
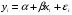 ,
, называются теоретическими параметрами (теоретическими коэффициентами) регрессии;
называются теоретическими параметрами (теоретическими коэффициентами) регрессии; 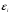 - случайным отклонением (случайной ошибкой).
- случайным отклонением (случайной ошибкой). .
.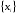 ,
, 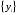 необходимо оценить значения параметров
необходимо оценить значения параметров  ,
, теоретические значения зависимой переменной y,
теоретические значения зависимой переменной y, 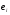 - наблюдаемые значения ошибок
- наблюдаемые значения ошибок 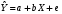 .
.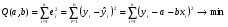 .
. ), поэтому она достигает минимума. Необходимым условием существования минимума является равенство нулю её частных производных по a и b:
), поэтому она достигает минимума. Необходимым условием существования минимума является равенство нулю её частных производных по a и b: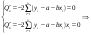
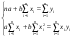 .
.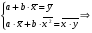
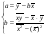 или
или 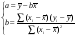
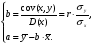
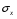 и
и 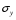 средние квадратические отклонения значений тех же признаков.
средние квадратические отклонения значений тех же признаков.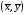 , а коэффициент регрессии b пропорционален показателю ковариации и коэффициенту линейной корреляции.
, а коэффициент регрессии b пропорционален показателю ковариации и коэффициенту линейной корреляции.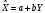 , где
, где 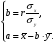 ), то произведение коэффициентов
), то произведение коэффициентов  :
: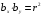 .
.
 это величина, показывающая, на сколько единиц размерности изменится величина
это величина, показывающая, на сколько единиц размерности изменится величина 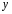 при изменении величины
при изменении величины  на одну единицу ее размерности. Аналогично определяется коэффициент
на одну единицу ее размерности. Аналогично определяется коэффициент  .
.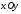 , проходящих внутри соответствующего корреляционного поля. Такие линии называются линиями регрессии.
, проходящих внутри соответствующего корреляционного поля. Такие линии называются линиями регрессии.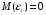 ;
;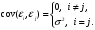
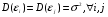 ;
;