Лекция по эконометрике. Лекция по эконометрике
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
|
2.1 Оценка общего качества уравнения регрессии Для анализа общего качества полученного уравнения регрессии на количественном уровне используют коэффициент детерминации 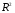 . Он рассчитывается по формуле: . Он рассчитывается по формуле: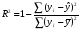 . .В числителе вычитаемой из единицы дроби стоит сумма квадратов отклонений (СКО) выборочных значений зависимой переменной от теоретических, найденных с помощью уравнения регрессии 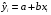 . В знаменателе – СКО наблюдений зависимой переменной от среднего значения. . В знаменателе – СКО наблюдений зависимой переменной от среднего значения.Коэффициент детерминации характеризует долю вариации (разброса) зависимой переменной, объяснённой с помощью данного уравнения. Замечание. В случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента линейной корреляции. Более точным является значение коэффициента детерминации с поправкой на число степеней свободы. Разделив каждую СКО на свое число степеней свободы, получим средний квадрат отклонений, или дисперсию на одну степень свободы: 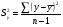 – дисперсия, характеризующая общий разброс; – дисперсия, характеризующая общий разброс;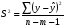 – остаточная дисперсия, где m – число независимых (объясняющих) переменных, в случае парной регрессии m =1 и формула имеет вид: – остаточная дисперсия, где m – число независимых (объясняющих) переменных, в случае парной регрессии m =1 и формула имеет вид: 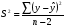 . .Учитывая приведённые выше обозначения, формула коэффициента детерминации с поправкой на число степеней свободы будет иметь вид: 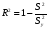 . .Значения коэффициента 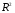 изменяются от 0 до +1 (в редких случаях значение может быть и отрицательным числом). изменяются от 0 до +1 (в редких случаях значение может быть и отрицательным числом).Близость коэффициента детерминации к +1 свидетельствует о том, что существует статистически значимая линейная связь между переменными, а уравнение имеет хорошее качество. Близость 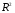 к 0 говорит о том, что просто горизонтальная прямая к 0 говорит о том, что просто горизонтальная прямая 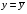 является лучшей по сравнению с найденной регрессионной прямой. является лучшей по сравнению с найденной регрессионной прямой.Самостоятельную важность коэффициент детерминации приобретает только в случае множественной регрессии. 2.2 Оценка существенности параметров линейной регрессии и всего уравнения в целом После того, как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включённых в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Проверка значимости производится на основе дисперсионного анализа. Согласно идее дисперсионного анализа, общая сумма квадратов отклонений (СКО) y от среднего значения 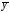 раскладывается на две части – объясненную и необъясненную: раскладывается на две части – объясненную и необъясненную: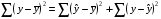 или, соответственно: 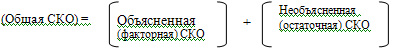 Здесь возможны два крайних случая: когда общая СКО в точности равна остаточной и когда общая СКО равна факторной. В первом случае фактор х не оказывает влияния на результат, вся дисперсия y обусловлена воздействием прочих факторов, линия регрессии параллельна оси Ох и уравнение должно иметь вид 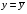 . .Во втором случае прочие факторы не влияют на результат, y связан с x функционально, и остаточная СКО равна нулю. Однако на практике в правой части присутствуют оба слагаемых. Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации y приходится на объясненную вариацию. Если объясненная СКО будет больше остаточной СКО, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат y. Это равносильно тому, что коэффициент детерминации будет приближаться к единице. Число степеней свободы (df-degrees of freedom) – это число независимо варьируемых значений признака. Для общей СКО требуется (n-1) независимых отклонений, 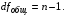 Факторная СКО имеет одну степень свободы, и 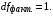 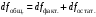 Таким образом, можем записать: 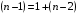 Из этого баланса определяем, что 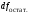 = n–2. = n–2.Разделив каждую СКО на свое число степеней свободы, получим средний квадрат отклонений, или дисперсию на одну степень свободы: 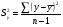 - общая дисперсия, - общая дисперсия, 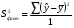 - факторная, - факторная, 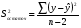 - остаточная. - остаточная.Анализ статистической значимости коэффициентов линейной регрессии Хотя теоретические значения коэффициентов  уравнения линейной зависимости уравнения линейной зависимости 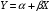 предполагаются постоянными величинами, оценки а и b этих коэффициентов, получаемые в ходе построения уравнения по данным случайной выборки, являются случайными величинами. Если ошибки регрессии имеют нормальное распределение, то оценки коэффициентов также распределены нормально и могут характеризоваться своими средними значениями и дисперсией. Поэтому анализ коэффициентов начинается с расчёта этих характеристик. предполагаются постоянными величинами, оценки а и b этих коэффициентов, получаемые в ходе построения уравнения по данным случайной выборки, являются случайными величинами. Если ошибки регрессии имеют нормальное распределение, то оценки коэффициентов также распределены нормально и могут характеризоваться своими средними значениями и дисперсией. Поэтому анализ коэффициентов начинается с расчёта этих характеристик.Дисперсии коэффициентов рассчитываются по формулам: Дисперсия коэффициента регрессии 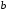 : : 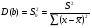 , ,где 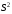 – остаточная дисперсия на одну степень свободы. – остаточная дисперсия на одну степень свободы.Дисперсия параметра 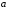 : :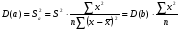 Отсюда стандартная ошибка коэффициента регрессии 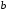 определяется по формуле: определяется по формуле: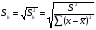 , ,Стандартная ошибка параметра 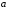 определяется по формуле: определяется по формуле: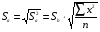 . .Далее рассчитываются t – статистики: 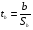 , , 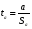 Они служат для проверки нулевых гипотез о том, что истинное значение коэффициента регрессии b или свободного члена a равно нулю: 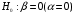 . .Альтернативная гипотеза имеет вид: 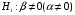 . .t – статистики имеют t – распределение Стьюдента с 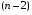 степенями свободы. По таблицам распределения Стьюдента при определённом уровне значимости α и степенями свободы. По таблицам распределения Стьюдента при определённом уровне значимости α и 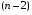 степенях свободы находят критическое значение степенях свободы находят критическое значение 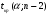 . .Если 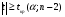 , то нулевая гипотеза должна быть отклонена, коэффициенты считаются статистически значимыми. , то нулевая гипотеза должна быть отклонена, коэффициенты считаются статистически значимыми.Если 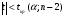 , то нулевая гипотеза не может быть отклонена. (В случае, если коэффициент b статистически незначим, уравнение должно иметь вид , то нулевая гипотеза не может быть отклонена. (В случае, если коэффициент b статистически незначим, уравнение должно иметь вид 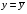 , и это означает, что связь между признаками отсутствует. В случае, если коэффициент а статистически незначим, рекомендуется оценить новое уравнение в виде , и это означает, что связь между признаками отсутствует. В случае, если коэффициент а статистически незначим, рекомендуется оценить новое уравнение в виде 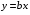 ). ).Интервальные оценки коэффициентов линейного уравнения регрессии: Доверительный интервал для а: 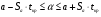 . .Доверительный интервал для b: 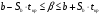 Это означает, что с заданной надёжностью 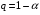 (где (где 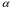 - уровень значимости) истинные значения а, b находятся в указанных интервалах. - уровень значимости) истинные значения а, b находятся в указанных интервалах.Коэффициент регрессии имеет четкую экономическую интерпретацию, поэтому доверительные границы интервала не должны содержать противоречивых результатов, например, 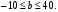 Они не должны включать нуль. Они не должны включать нуль.Анализ статистической значимости уравнения в целом. Распределение Фишера в регрессионном анализе Оценка значимости уравнения регрессии в целом дается с помощью F- критерия Фишера. При этом выдвигается нулевая гипотеза 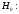 о том, что все коэффициенты регрессии, за исключением свободного члена а, равны нулю и, следовательно, фактор х не оказывает влияния на результат y ( о том, что все коэффициенты регрессии, за исключением свободного члена а, равны нулю и, следовательно, фактор х не оказывает влияния на результат y (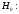 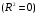 или или 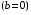 ). ).Величина F – критерия связана с коэффициентом детерминации. В случае множественной регрессии: 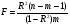 , ,где m – число независимых переменных. В случае парной регрессии формула F – статистики принимает вид: 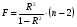 . .При нахождении табличного значения F- критерия задается уровень значимости (обычно 0,05 или 0,01) и две степени свободы: 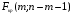 – в случае множественной регрессии, – в случае множественной регрессии, 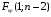 – для парной регрессии. – для парной регрессии.Если 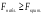 , то , то 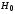 отклоняется и делается вывод о существенности статистической связи между y и x. отклоняется и делается вывод о существенности статистической связи между y и x.Если 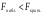 , то вероятность уравнение регрессии считается статистически незначимым, , то вероятность уравнение регрессии считается статистически незначимым, 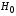 не отклоняется. не отклоняется.Замечание. В парной линейной регрессии 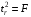 . Кроме того, . Кроме того, 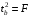 , поэтому , поэтому 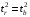 . Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии. . Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.Распределение Фишера может быть использовано не только для проверки гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии, но и гипотезы о равенстве нулю части этих коэффициентов. Это важно при развитии линейной регрессионной модели, так как позволяет оценить обоснованность исключения отдельных переменных или их групп из числа объясняющих переменных, или же, наоборот, включения их в это число. Пусть, например, вначале была оценена множественная линейная регрессия 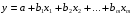 по п наблюдениям с т объясняющими переменными, и коэффициент детерминации равен по п наблюдениям с т объясняющими переменными, и коэффициент детерминации равен 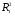 , затем последние k переменных исключены из числа объясняющих, и по тем же данным оценено уравнение , затем последние k переменных исключены из числа объясняющих, и по тем же данным оценено уравнение 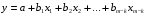 , для которого коэффициент детерминации равен , для которого коэффициент детерминации равен 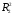 ( (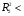 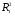 , т.к. каждая дополнительная переменная объясняет часть , пусть небольшую, вариации зависимой переменной). , т.к. каждая дополнительная переменная объясняет часть , пусть небольшую, вариации зависимой переменной).Для того, чтобы проверить гипотезу об одновременном равенстве нулю всех коэффициентов при исключённых переменных, рассчитывается величина 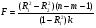 , ,имеющая распределение Фишера с 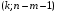 степенями свободы. степенями свободы.По таблицам распределения Фишера, при заданном уровне значимости, находят 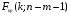 . И если . И если 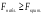 , то нулевая гипотеза отвергается. В таком случае исключать все k переменных из уравнения некорректно. , то нулевая гипотеза отвергается. В таком случае исключать все k переменных из уравнения некорректно.Аналогичные рассуждения могут быть проведены и по поводу обоснованности включения в уравнение регрессии одной или нескольких k новых объясняющих переменных. В этом случае рассчитывается F – статистика 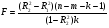 , ,имеющая распределение 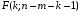 . И если она превышает критический уровень, то включение новых переменных объясняет существенную часть необъяснённой ранее дисперсии зависимой переменной (т.е. включение новых объясняющих переменных оправдано). . И если она превышает критический уровень, то включение новых переменных объясняет существенную часть необъяснённой ранее дисперсии зависимой переменной (т.е. включение новых объясняющих переменных оправдано).Замечания. 1. Включать новые переменные целесообразно по одной. 2. Для расчёта F – статистики при рассмотрении вопроса о включении объясняющих переменных в уравнение желательно рассматривать коэффициент детерминации с поправкой на число степеней свободы. F – статистика Фишера используется также для проверки гипотезы о совпадении уравнений регрессии для отдельных групп наблюдений. Пусть имеются 2 выборки, содержащие, соответственно, 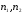 наблюдений. Для каждой из этих выборок оценено уравнение регрессии вида наблюдений. Для каждой из этих выборок оценено уравнение регрессии вида 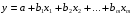 . Пусть СКО . Пусть СКО 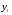 от линии регрессии (т.е. от линии регрессии (т.е. 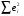 ) равны для них, соответственно, ) равны для них, соответственно, 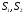 . .Проверяется нулевая гипотеза 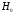 : о том, что все соответствующие коэффициенты этих уравнений равны друг другу, т.е. уравнение регрессии для этих выборок одно и то же. : о том, что все соответствующие коэффициенты этих уравнений равны друг другу, т.е. уравнение регрессии для этих выборок одно и то же.Пусть оценено уравнение регрессии того же вида сразу для всех 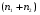 наблюдений, и СКО наблюдений, и СКО 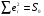 . .Тогда рассчитывается F – статистика по формуле: 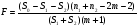 Она имеет распределение Фишера с 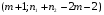 степенями свободы. F – статистика будет близкой к нулю, если уравнение для обеих выборок одинаково, т.к. в этом случае степенями свободы. F – статистика будет близкой к нулю, если уравнение для обеих выборок одинаково, т.к. в этом случае 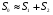 . Т.е. если . Т.е. если 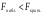 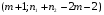 , то нулевая гипотеза принимается. , то нулевая гипотеза принимается.Если же 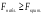 , то нулевая гипотеза отвергается, и единое уравнение регрессии построить нельзя. , то нулевая гипотеза отвергается, и единое уравнение регрессии построить нельзя.2.3 Проверка предпосылок, лежащих в основе МНК Следующим этапом оценивания качества уравнения является проверка выполнения предпосылок, лежащих в основе метода расчёта параметров МНК. Предпосылками МНК являются: 1. случайный характер ошибок регрессии; 2. нулевая средняя величина ошибок регрессии, не зависящая от значения объясняющих переменных; 3. независимость распределения ошибок для различных наблюдений; в случае оценки уравнения на временных рядах – отсутствие автокорреляции ошибок; 4. постоянство дисперсии ошибок, её независимость от значений объясняющих переменных – гомоскедастичность (если эта предпосылка не выполняется, то имеет место гетероскедастичность ошибок); 5. нормальность распределения ошибок регрессии. Для проверки выполнения каждой из предпосылок применения МНК имеются специальные тесты. Реализация многих из этих тестов предполагает значительный объём исходных данных. Если распределение случайных ошибок 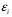 не соответствует некоторым предпосылкам МНК, то следует корректировать модель. не соответствует некоторым предпосылкам МНК, то следует корректировать модель.Проверка первой предпосылки МНК Прежде всего, проверяется случайный характер остатков 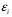 – первая предпосылка МНК. С этой целью стоится график зависимости остатков – первая предпосылка МНК. С этой целью стоится график зависимости остатков 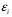 от теоретических значений результативного признака (рис. 1). Если на графике получена горизонтальная полоса, то остатки от теоретических значений результативного признака (рис. 1). Если на графике получена горизонтальная полоса, то остатки 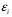 представляют собой случайные величины и МНК оправдан, теоретические значения представляют собой случайные величины и МНК оправдан, теоретические значения 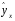 хорошо аппроксимируют фактические значения хорошо аппроксимируют фактические значения 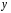 . .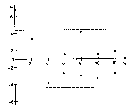 Рис. 1. Зависимость случайных остатков 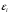 от теоретических значений от теоретических значений 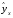 . .Возможны следующие случаи, если 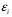 зависит от зависит от 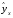 то: то: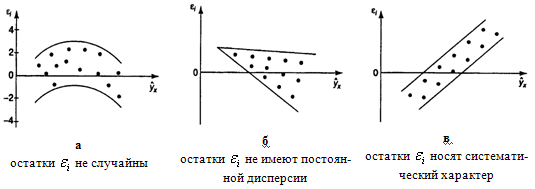 Рис. 2. Зависимость случайных остатков 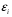 от теоретических значений от теоретических значений 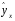 . .В этих случаях необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки 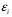 не будут случайными величинами. не будут случайными величинами.Проверка второй предпосылки МНК Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что 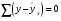 (или (или 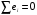 ). Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных. ). Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.Вместе с тем, несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от независимости случайных остатков и величин 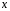 , что также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью наряду с изложенным графиком зависимости остатков , что также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью наряду с изложенным графиком зависимости остатков 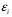 от теоретических значений результативного признака от теоретических значений результативного признака 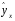 строится график зависимости случайных остатков строится график зависимости случайных остатков 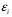 от факторов, включенных в регрессию от факторов, включенных в регрессию 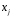 (рис. 3). (рис. 3).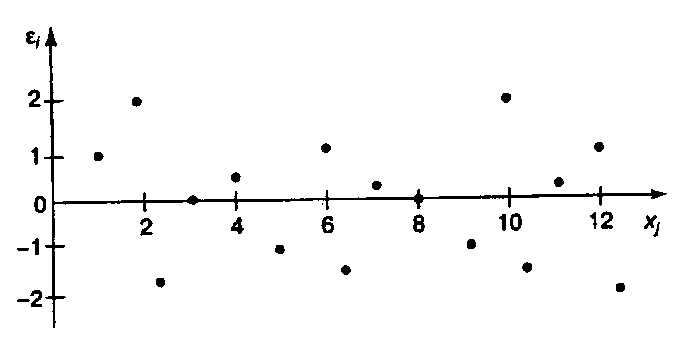 Рис. .3. Зависимость величины остатков от величины фактора 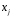 . .Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений 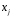 . Если же график показывает наличие зависимости . Если же график показывает наличие зависимости 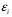 и и 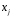 , то модель неадекватна. Причины неадекватности могут быть разные. Возможно, что нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора , то модель неадекватна. Причины неадекватности могут быть разные. Возможно, что нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора 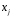 . Может быть неправильна спецификация модели и в нее необходимо ввести дополнительные члены от . Может быть неправильна спецификация модели и в нее необходимо ввести дополнительные члены от 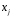 , например , например 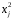 . Скопление точек в определенных участках значений фактора . Скопление точек в определенных участках значений фактора 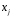 говорит о наличии систематической погрешности модели. говорит о наличии систематической погрешности модели.Замечание. Предпосылка о нормальном распределении остатков (пятая предпосылка) позволяет проводить проверку параметров регрессии и корреляции с помощью 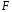 - и - и 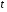 -критериев. Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т.е. при нарушении пятой предпосылки МНК. -критериев. Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т.е. при нарушении пятой предпосылки МНК.Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей и четвертой предпосылок. Автокорреляция ошибок. Статистика Дарбина-Уотсона Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений 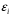 от значений отклонений во всех других наблюдениях. Отсутствие зависимости гарантирует отсутствие коррелированности между любыми отклонениями, т.е. от значений отклонений во всех других наблюдениях. Отсутствие зависимости гарантирует отсутствие коррелированности между любыми отклонениями, т.е. 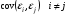 и, в частности, между соседними отклонениями и, в частности, между соседними отклонениями 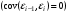 . .Автокорреляция (последовательная корреляция) остатков определяется как корреляция между соседними значениями случайных отклонений во времени (временные ряды) или в пространстве (перекрестные данные). Она обычно встречается во временных рядах и очень редко – в пространственных данных. Возможны следующие случаи: 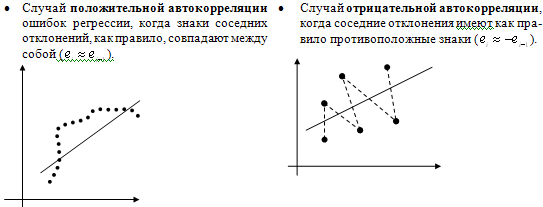 Эти случаи могут свидетельствовать о возможности улучшить уравнение путём оценивания новой нелинейной формулы или включения новой объясняющей переменной. В экономических задачах значительно чаще встречается положительная автокорреляция, чем отрицательная автокорреляция. Если же характер отклонений случаен, то можно предположить, что в половине случаев знаки соседних отклонений совпадают, а в половине – различны. Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.
От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму модели, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции в остатках. Для обнаружения автокорреляции используют либо графический метод. Либо статистические тесты. Графический метод заключается в построении графика зависимости ошибок от времени (в случае временных рядов) или от объясняющих переменных и визуальном определении наличия или отсутствия автокорреляции. Наиболее известный критерий обнаружения автокорреляции первого порядка – критерий Дарбина-Уотсона. Статистика DW Дарбина-Уотсона приводится во всех специальных компьютерных программах как одна из важнейших характеристик качества регрессионной модели. Сначала по построенному эмпирическому уравнению регрессии определяются значения отклонений 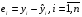 . А затем рассчитывается статистика Дарбина-Уотсона по формуле: . А затем рассчитывается статистика Дарбина-Уотсона по формуле: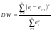 . .Статистика DW изменяется от 0 до 4. DW=0 соответствует положительной автокорреляции, при отрицательной автокорреляции DW=4. Когда автокорреляция отсутствует, коэффициент автокорреляции равен нулю, и статистика DW = 2. Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза 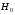 об отсутствии автокорреляции остатков. Альтернативные гипотезы об отсутствии автокорреляции остатков. Альтернативные гипотезы 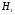 и и 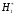 состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона 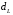 (- нижняя граница признания положительной автокорреляции) и (- нижняя граница признания положительной автокорреляции) и 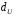 (-верхняя граница признания отсутствия положительной автокорреляции) для заданного числа наблюдений (-верхняя граница признания отсутствия положительной автокорреляции) для заданного числа наблюдений 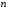 , числа независимых переменных модели , числа независимых переменных модели 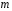 и уровня значимости и уровня значимости 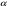 . По этим значениям числовой промежуток . По этим значениям числовой промежуток 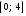 разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью 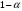 осуществляется следующим образом: осуществляется следующим образом: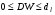 – положительная автокорреляция, принимается – положительная автокорреляция, принимается 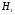 ; ;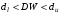 – зона неопределенности; – зона неопределенности;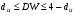 – автокорреляция отсутствует; – автокорреляция отсутствует;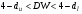 – зона неопределенности; – зона неопределенности;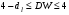 – отрицательная автокорреляция, принимается – отрицательная автокорреляция, принимается 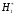 . .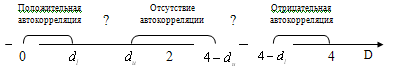 Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу 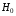 . .Можно показать, что статистика DW тесно связана с коэффициентом автокорреляции первого порядка: 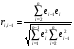 Связь выражается формулой: 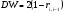 . .Значения r изменяются от –1 (в случае отрицательной автокорреляции) до +1 (в случае положительной автокорреляции). Близость r к нулю свидетельствует об отсутствии автокорреляции. При отсутствии таблиц критических значений DW можно использовать следующее "грубое" правило: при достаточном числе наблюдений (12-15), при 1-3 объясняющих переменных, если 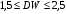 , то отклонения от линии регрессии можно считать взаимно независимыми. , то отклонения от линии регрессии можно считать взаимно независимыми.Либо применить к данным уменьшающее автокорреляцию преобразование (например автокорреляционное преобразование или метод скользящих средних). Существует несколько ограничений на применение критерия Дарбина-Уотсона.
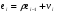 , ,называемой авторегрессионной схемой первого порядка AR(1). Здесь 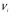 – случайный член. – случайный член.
Для авторегрессионных моделей предлагается h – статистика Дарбина 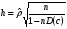 , ,где 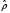 – оценка коэффициента автокорреляции первого порядка, D(c) – выборочная дисперсия коэффициента при лаговой переменной yt-1, n – число наблюдений. – оценка коэффициента автокорреляции первого порядка, D(c) – выборочная дисперсия коэффициента при лаговой переменной yt-1, n – число наблюдений.Обычно значение 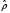 рассчитывается по формуле рассчитывается по формуле 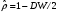 , а D(c) равна квадрату стандартной ошибки Sc оценки коэффициента с. , а D(c) равна квадрату стандартной ошибки Sc оценки коэффициента с.Методы устранения автокорреляции. Авторегрессионное преобразование В случае наличия автокорреляции остатков полученная формула регрессии обычно считается неудовлетворительной. Автокорреляция ошибок первого порядка говорит о неверной спецификации модели. Поэтому следует попытаться скорректировать саму модель. Посмотрев на график ошибок, можно поискать другую (нелинейную) формулу зависимости, включить неучтённые до этого факторы, уточнить период проведения расчётов или разбить его на части. Если все эти способы не помогают и автокорреляция вызвана какими–то внутренними свойствами ряда {ei}, можно воспользоваться преобразованием, которое называется авторегрессионной схемой первого порядка AR(1). (Авторегрессией это преобазование называется потому, что значение ошибки 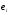 определяется значением той же самой величины, но с запаздыванием. Т.к. максимальное запаздывание равно 1, то это авторегрессия первого порядка). определяется значением той же самой величины, но с запаздыванием. Т.к. максимальное запаздывание равно 1, то это авторегрессия первого порядка).Формула AR(1) имеет вид: 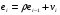 . .Где 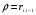 -коэффициент автокорреляции первого порядка ошибок регрессии. -коэффициент автокорреляции первого порядка ошибок регрессии.Рассмотрим AR(1) на примере парной регрессии: 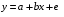 . .Тогда соседним наблюдениям соответствует формула: 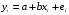 (1), (1),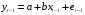 (2). (2).Умножим (2) на 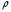 и вычтем из (1): и вычтем из (1):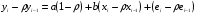 . .Сделаем замены переменных 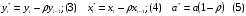 получим с учетом 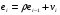 : :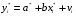 (6). (6).Это преобразование называется авторегрессионным (преобразованием Бокса-Дженкинса). Поскольку случайные отклонения 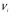 удовлетворяют предпосылкам МНК, оценки а* и b будут обладать свойствами наилучших линейных несмещенных оценок. По преобразованным значениям всех переменных с помощью обычного МНК вычисляются оценки параметров а* и b, которые затем можно использовать в регрессии. удовлетворяют предпосылкам МНК, оценки а* и b будут обладать свойствами наилучших линейных несмещенных оценок. По преобразованным значениям всех переменных с помощью обычного МНК вычисляются оценки параметров а* и b, которые затем можно использовать в регрессии.Т.о. если остатки по исходному уравнению регрессии автокоррелированы, то для оценки параметров уравнения используют следующие преобразования: 1) Преобразовать исходные переменные у и х к виду (3), (4). 2) Обычным МНК для уравнения (6) определить оценки а* и b. 3) Рассчитать параметр а исходного уравнения из соотношения (4) 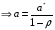 . .4) Записать исходное уравнение (1) с параметрами а и b (где а - из п.3, а b берётся непосредственно из уравнения (6)). Авторегрессионное преобразование может быть обобщено на произвольное число объясняющих переменных, т.е. использовано для уравнения множественной регрессии. Для преобразования AR(1) важно оценить коэффициент автокорреляции ρ. Это делается несколькими способами. Самое простое – оценить ρ на основе статистики DW: 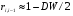 , ,где r берется в качестве оценки ρ. Этот метод хорошо работает при большом числе наблюдений. В случае, когда есть основания считать, что положительная автокорреляция отклонений очень велика ( 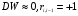 ), можно использовать метод первых разностей (метод исключения тенденции), уравнение принимает вид ), можно использовать метод первых разностей (метод исключения тенденции), уравнение принимает вид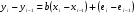 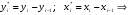 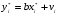 . .Из уравнения по МНК оценивается коэффициент b. Параметр а здесь не определяется непосредственно, однако из МНК известно, что 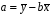 . .В случае полной отрицательной автокорреляции отклонений ( 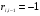 ) )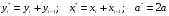 , ,получаем уравнение регрессии: 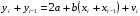 или 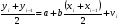 . .Вычисляются средние за 2 периода, а затем по ним рассчитывают а и b. Данная модель называется моделью регрессии по скользящим средним. Проверка гомоскедастичности дисперсии ошибок В соответствии с четвёртой предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора 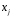 остатки остатки 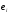 имеют одинаковую дисперсию имеют одинаковую дисперсию 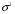 . Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. . Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность.В качестве примера реальной гетероскедастичности можно привести то, что люди с большим доходом не только тратят в среднем больше, чем люди с меньшим доходом, но и разброс в их потреблении также больше, поскольку они имеют больше простора для распределения дохода. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (- графический метод обнаружения гетероскедастичности). 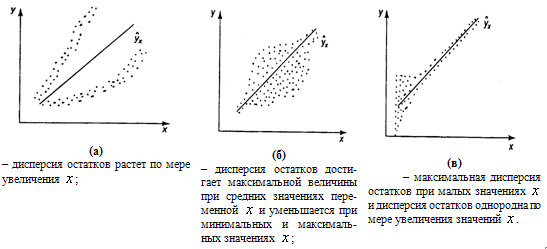 Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков 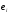 от теоретических значений результативного признака от теоретических значений результативного признака 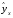 . .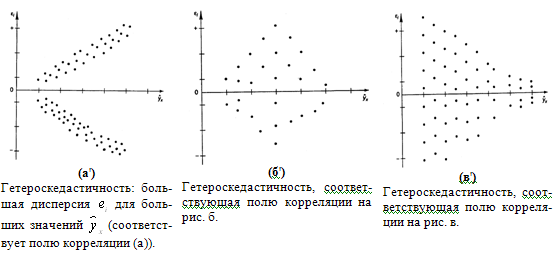 Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- и гетероскедастичности. При нарушении гомоскедастичности имеем неравенства: 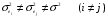 , где , где 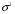 - постоянная дисперсия ошибки при соблюдении предпосылки. Т.е. можно записать, что дисперсия ошибки при - постоянная дисперсия ошибки при соблюдении предпосылки. Т.е. можно записать, что дисперсия ошибки при 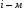 наблюдении пропорциональна постоянной дисперсии: наблюдении пропорциональна постоянной дисперсии:  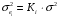 . .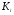 - коэффициент пропорциональности. Он меняется при переходе от одного значения фактора - коэффициент пропорциональности. Он меняется при переходе от одного значения фактора 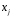 к другому. к другому.Задача состоит в том, чтобы определить величину 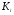 и внести поправку в исходные переменные. При этом используют обобщённый МНК, который эквивалентен обычному МНК, применённому к преобразованным данным. и внести поправку в исходные переменные. При этом используют обобщённый МНК, который эквивалентен обычному МНК, применённому к преобразованным данным.Чтобы убедиться в обоснованности использования обобщённого МНК проводят эмпирическое подтверждение наличия гетероскедастичности. При малом объёме выборки, что наиболее характерно для эмпирических исследований, для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта (в 1965 г. они рассмотрели модель парной линейной регрессии, в которой дисперсия ошибок пропорциональна квадрату фактора). Пусть рассматривается модель, в которой дисперсия 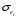 пропорциональна квадрату фактора: пропорциональна квадрату фактора: 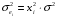 , , 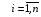 . А также остатки имеют нормальное распределение и отсутствует автокорреляция остатков. . А также остатки имеют нормальное распределение и отсутствует автокорреляция остатков.Параметрический тест (критерий) Гольдфельда – Квандта: 1. Все n наблюдений в выборке упорядочиваются по величине x. 2. Вся упорядоченная выборка разбивается на три подвыборки (объёмом k, С, k.) 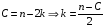 . .Исключаются из рассмотрения С центральных наблюдений. (По рекомендациям специалистов, объём исключаемых данных С должен быть примерно равен четверти общего объёма выборки n, в частности, при n =20, С=4; при n =30, С = 8; при n =60, С=16). 3. Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для последней подвыборки (k последних наблюдений). 4. Определяются остаточные суммы квадратов 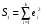 для первой и второй для первой и второй 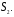 групп. Если предположение о пропорциональности дисперсий отклонений значениям x верно, то групп. Если предположение о пропорциональности дисперсий отклонений значениям x верно, то 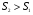 . .5. Выдвигается нулевая гипотеза 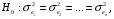 которая предполагает отсутствие гетероскедастичности. которая предполагает отсутствие гетероскедастичности.Для проверки этой гипотезы рассчитывается отношение 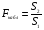 , ,которое имеет распределение Фишера с 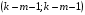 степеней свободы (здесь m – число объясняющих переменных). степеней свободы (здесь m – число объясняющих переменных).Если 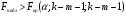 , то гипотеза об отсутствии гетероскедастичности отклоняется при уровне значимости α. , то гипотеза об отсутствии гетероскедастичности отклоняется при уровне значимости α.Этот же тест может быть использован и при предположении об обратной пропорциональности между дисперсией и значениями объясняющей переменной 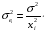 . В этом случае статистика Фишера принимает вид: . В этом случае статистика Фишера принимает вид: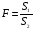 . .При установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии отклонений 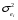 . Обобщенный метод наименьших квадратов (ОМНК) . Обобщенный метод наименьших квадратов (ОМНК)При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов заменять обобщенным методом наименьших квадратов (ОМНК). Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Остановимся на использовании ОМНК для корректировки гетероскедастичности. Рассмотрим ОМНК для корректировки гетероскедастичности. Будем предполагать, что среднее значение остаточных величин равно нулю 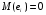 , а дисперсия пропорциональна величине , а дисперсия пропорциональна величине 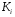 . .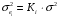 , ,где 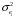 – дисперсия ошибки при конкретном – дисперсия ошибки при конкретном 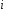 -м значении фактора; -м значении фактора; 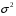 – постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; – постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; 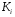 – коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии. – коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.При этом предполагается, что 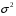 неизвестна, а в отношении величин неизвестна, а в отношении величин 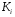 выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности. выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.В общем виде для уравнения 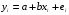 модель примет вид: модель примет вид: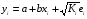 . .В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе 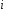 -го наблюдения, на -го наблюдения, на 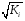 . Тогда дисперсия остатков будет величиной постоянной, т. е. . Тогда дисперсия остатков будет величиной постоянной, т. е. 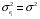 . .Иными словами, от регрессии 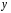 по по 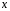 мы перейдем к регрессии на новых переменных: мы перейдем к регрессии на новых переменных: 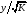 и и 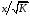 . Уравнение регрессии примет вид: . Уравнение регрессии примет вид: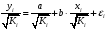 , ,а исходные данные для данного уравнения будут иметь вид: 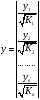 , ,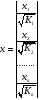 . .По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные 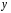 и и 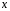 взяты с весами взяты с весами 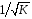 . .Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отклонений вида 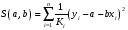 . .Соответственно получим следующую систему нормальных уравнений: 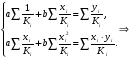 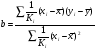 , ,Т.е. коэффициент регрессии 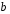 при использовании обобщенного МНК с целью корректировки гетероскедастичности представляет собой взвешенную величину по отношению к обычному МНК с весом при использовании обобщенного МНК с целью корректировки гетероскедастичности представляет собой взвешенную величину по отношению к обычному МНК с весом 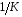 . .Если преобразованные переменные 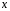 и и 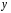 взять в отклонениях от средних уровней, то коэффициент регрессии взять в отклонениях от средних уровней, то коэффициент регрессии 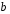 можно определить как можно определить как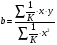 . .При обычном применении метода наименьших квадратов к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии 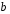 определяется по формуле: определяется по формуле: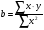 . .Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Для применения ОМНК необходимо знать фактические значения дисперсий отклонений 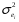 . На практике такие значения известны крайне редко. Поэтому, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях . На практике такие значения известны крайне редко. Поэтому, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях 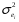 . В эконометрических исследованиях чаще всего предполагается, что дисперсии отклонений пропорциональны или значениям xi, или значениям . В эконометрических исследованиях чаще всего предполагается, что дисперсии отклонений пропорциональны или значениям xi, или значениям 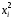 , т.е , т.е 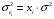 или или 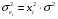 . .Если предположить, что дисперсии пропорциональны значениям фактора x, т.е. 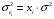 , тогда уравнение парной регрессии , тогда уравнение парной регрессии 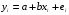 преобразуется делением его левой и правой частей на преобразуется делением его левой и правой частей на 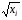 : :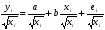 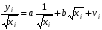 . .Здесь для случайных отклонений 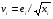 выполняется условие гомоскедастичности. Следовательно, для регрессии применим обычный МНК. Следует отметить, что новая регрессия не имеет свободного члена, но зависит от двух факторов. Оценив для неё по МНК коэффициенты а и b, возвращаемся к исходному уравнению регрессии. выполняется условие гомоскедастичности. Следовательно, для регрессии применим обычный МНК. Следует отметить, что новая регрессия не имеет свободного члена, но зависит от двух факторов. Оценив для неё по МНК коэффициенты а и b, возвращаемся к исходному уравнению регрессии.Если предположить, что дисперсии 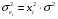 , то соответствующим преобразованием будет деление уравнения парной регрессии , то соответствующим преобразованием будет деление уравнения парной регрессии 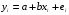 на xi: на xi: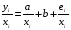 или, если переобозначить остатки как 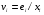 : :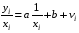 . .Здесь для отклонений vi также выполняется условие гомоскедастичности. В полученной регрессии по сравнению с исходным уравнением параметры поменялись ролями: свободный член а стал коэффициентом, а коэффициент b – свободным членом. Применяя обычный МНК в преобразованных переменных 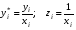 , ,получим оценки параметров, после чего возвращаемся к исходному уравнению. Пример. Рассматривая зависимость сбережений 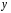 от дохода от дохода 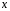 , по первоначальным данным было получено уравнение регрессии , по первоначальным данным было получено уравнение регрессии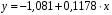 . .Применяя обобщенный МНК к данной модели в предположении, что ошибки пропорциональны доходу, было получено уравнение для преобразованных данных: 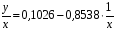 . .Коэффициент регрессии первого уравнения сравнивают со свободным членом второго уравнения, т.е. 0,1178 и 0,1026 – оценки параметра 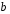 зависимости сбережений от дохода. зависимости сбережений от дохода.В случае множественной регрессии 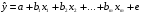 , ,Если предположить 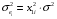 (т.е. дисперсия ошибок пропорциональна квадрату первой объясняющей переменной), то в этом случае обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения: (т.е. дисперсия ошибок пропорциональна квадрату первой объясняющей переменной), то в этом случае обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения: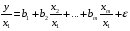 . .Следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным. Пример. Пусть 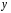 – издержки производства, – издержки производства, 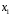 – объем продукции, – объем продукции, 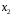 – основные производственные фонды, – основные производственные фонды, 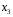 – численность работников, тогда уравнение – численность работников, тогда уравнение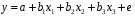 является моделью издержек производства с объемными факторами. Предполагая, что 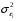 пропорциональна квадрату численности работников пропорциональна квадрату численности работников 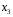 , мы получим в качестве результативного признака затраты на одного работника , мы получим в качестве результативного признака затраты на одного работника 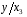 , а в качестве факторов следующие показатели: производительность труда , а в качестве факторов следующие показатели: производительность труда 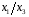 и фондовооруженность труда и фондовооруженность труда 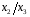 . Соответственно трансформированная модель примет вид . Соответственно трансформированная модель примет вид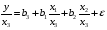 , ,где параметры 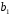 , , 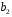 , , 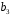 численно не совпадают с аналогичными параметрами предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на работника; с изменением производительности труда на единицу при неизменном уровне фовдовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда. численно не совпадают с аналогичными параметрами предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на работника; с изменением производительности труда на единицу при неизменном уровне фовдовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда.Если предположить, что в модели с первоначальными переменными дисперсия остатков пропорциональна квадрату объема продукции, 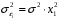 , можно перейти к уравнению регрессии вида , можно перейти к уравнению регрессии вида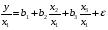 . .В нем новые переменные: 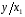 – затраты на единицу (или на 1 руб. продукции), – затраты на единицу (или на 1 руб. продукции), 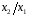 – фондоемкость продукции, – фондоемкость продукции, 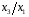 – трудоемкость продукции. – трудоемкость продукции.В заключение следует отметить, что обнаружении гетероскедастичности и её корректировка являются весьма серьёзной и трудоёмкой проблемой. В случае применения обобщённого (взвешенного) МНК необходима определённая информация или обоснованные предположения о величинах 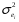 . . |

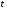 .
.