Лекция по эконометрике. Лекция по эконометрике
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
|
6. Временные ряды в эконометрических исследованиях 6.1 Выявление структуры временного ряда Временнóй ряд – это совокупность значений, какого – либо показателя за несколько последовательных моментов или периодов времени. Каждое значение (уровень) временного ряда формируется под воздействием большого числа факторов, которые можно условно разделить на три группы:
Тенденция характеризует долговременное воздействие факторов на динамику показателя. Тенденция может быть возрастающей или убывающей. 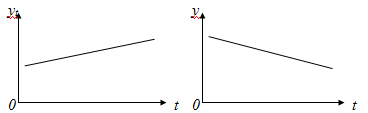 Циклические колебания могут носить сезонный характер или отражать динамику конъюнктуры рынка, а также фазу бизнес – цикла, в которой находится экономика страны. Реальные данные часто содержат все три компоненты. В большинстве случаев временной ряд можно представить как сумму или произведение трендовой 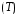 , циклической , циклической 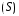 и случайной и случайной 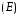 компонент. В случае суммы имеет место аддитивная модель временного ряда: компонент. В случае суммы имеет место аддитивная модель временного ряда: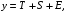 (1) в случае произведения – мультипликативная модель: (1) в случае произведения – мультипликативная модель: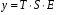 .(2) .(2)Основная задача эконометрического исследования отдельного временного ряда – выявление количественного выражения кждой из компонент и использование полученной информации для прогноза будущих значений ряда или построение модели взаимосвязи двух или более временных рядов.  Сначала рассмотрим основные подходы к анализу отдельного временного ряда. Такой ряд может содержать, помимо случайной составляющей, либо только тенденцию, либо только сезонную (циклическую) компоненту, либо все компоненты вместе. Для того, чтобы выявить наличие той или иной неслучайной компоненты, исследуется корреляционная зависимость между последовательными уровнями временного ряда, или автокорреляция уровней ряда. Основная идея такого анализа заключается в том, что при наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Количественно автокорреляцию можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Коэффициент автокорреляции уровней ряда первого порядка измеряет зависимость между соседними уровнями ряда 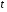 и и 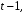 т.е. при лаге 1. т.е. при лаге 1.Он вычисляется по следующей формуле: 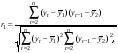 (3) (3)где в качестве средних величин берутся значения: 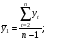 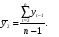 (4) (4)В первом случае усредняются значения ряда, начиная со второго до последнего, во втором случае – значения ряда с первого до предпоследнего. Формулу (3) можно представить как формулу выборочного коэффициента корреляции: 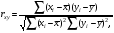 (5) (5)где в качестве переменной 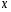 берется ряд берется ряд 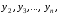 а в качестве переменной а в качестве переменной 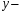 ряд ряд 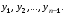 Если значение коэффициента (3) близко к единице, это указывает на очень тесную зависимость между соседними уровнями временного ряда и о наличии во временном ряде сильной линейной тенденции. Аналогично определяются коэффициенты автокорреляции более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями 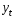 и и 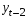 и определяется по формуле: и определяется по формуле: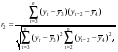 (6) (6)где в качестве одной средней величины берут среднюю уровней ряда с третьего до последнего, а в качестве другой – среднюю с первого уровня до 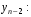 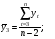 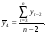 (7) (7)Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Для обеспечения статистической достоверности максимальный лаг, как считают некоторые известные эконометристы, не должен превышать четверти общего объема выборки. Коэффициент автокорреляции строится по аналогии с линейным коэффициентом корреляции, и поэтому он характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. По нему можно судить о наличии линейной или близкой к линейной тенденции. Однако для некоторых временных рядов с сильной нелинейной тенденцией (например, параболической или экспоненциальной), коэффициент автокорреляции уровней ряда может приближаться к нулю. Кроме того, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. |
