Ряды. Ряды. Основные понятия
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
|
Ряды. Основные понятия Бесконечные ряды широко используются в теоретических исследованиях математического анализа, имеют разнообразные практические применения. Числовым рядом (или просто рядом) называется выражение вида 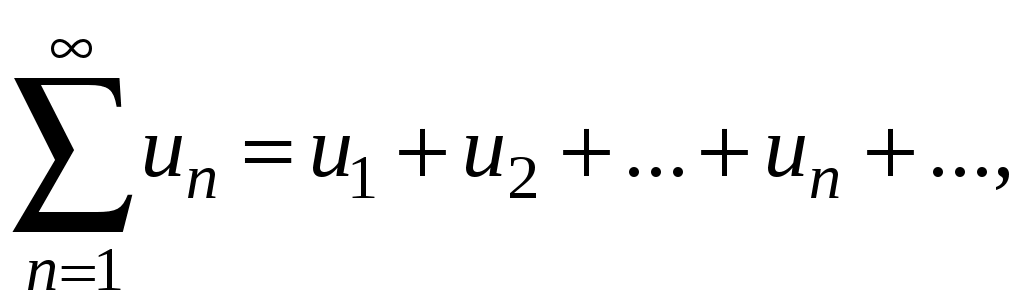 (1) (1)где Ряд (1) считается заданным, если известен общий член ряда Сумма первых n членов ряда (1) называется n-ой частичной суммой ряда и обозначается через Рассмотрим частичные суммы Если существует конечный предел 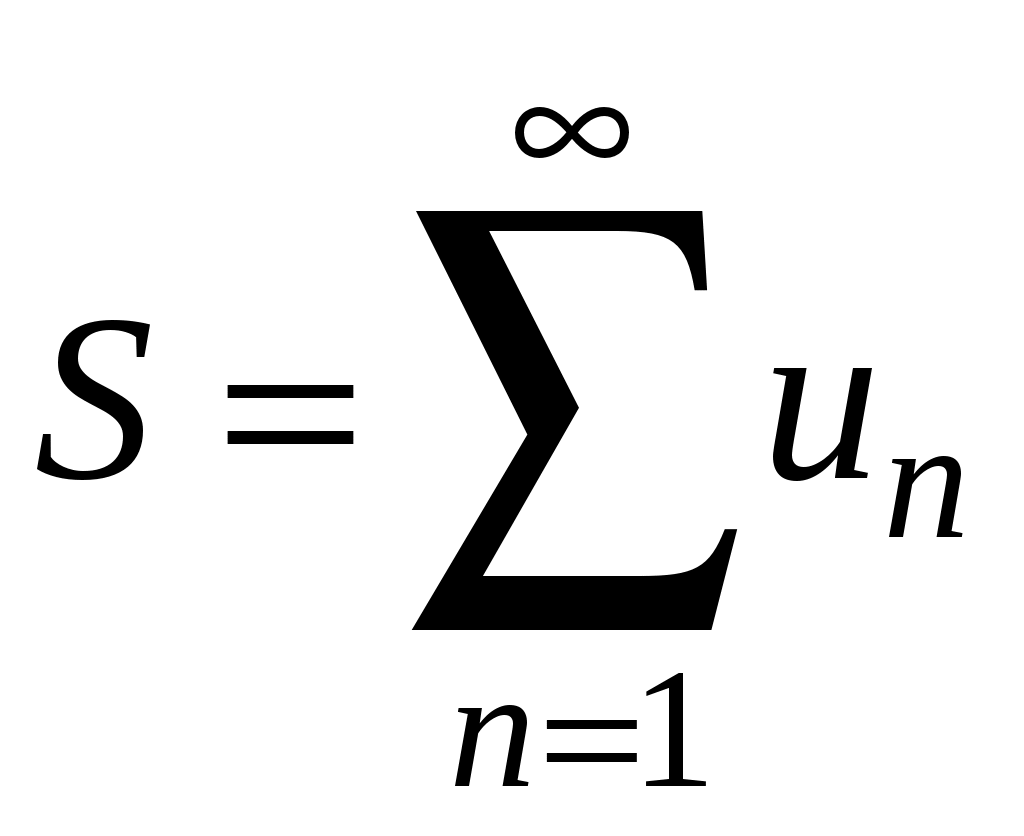 . .Если Рассмотрим примеры: 1. Ряд 2. Ряд 0 + 0 + 0 + … + 0 + … сходится, его сумма равна 0. 3. Ряд 1 + 1 + 1 + … + 1 + … расходится, 4. Ряд 1 – 1 + 1 – 1 + 1 – 1 + … расходится, так как последовательность частичных сумм 1, 0, 1, 0, 1, 0… 5. Ряд 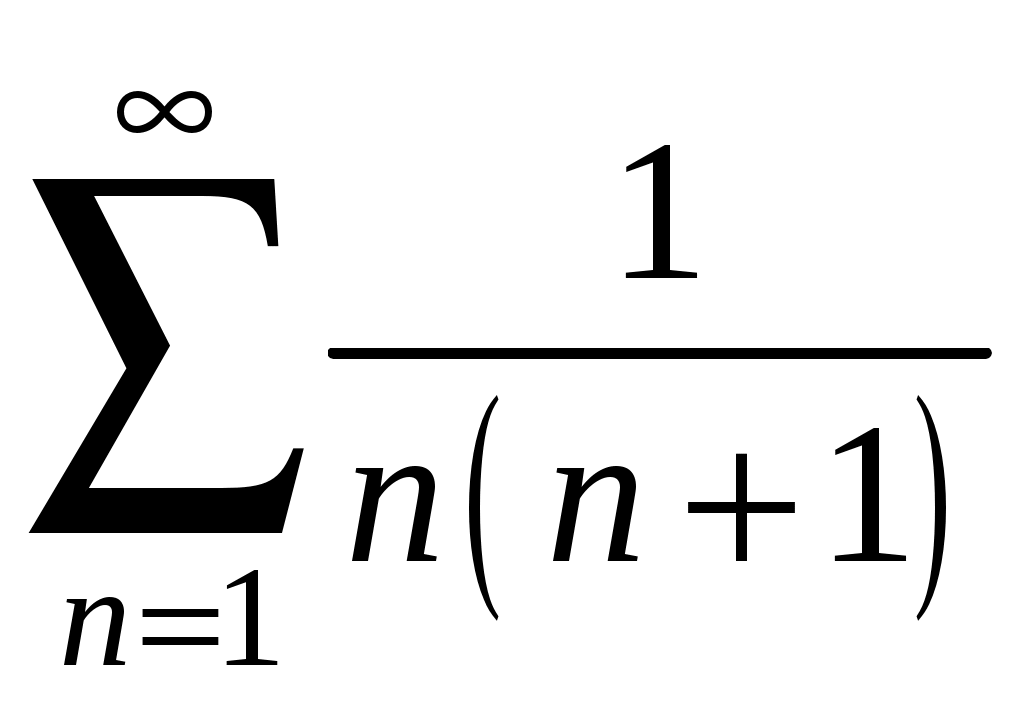 сходится. Действительно, сходится. Действительно, 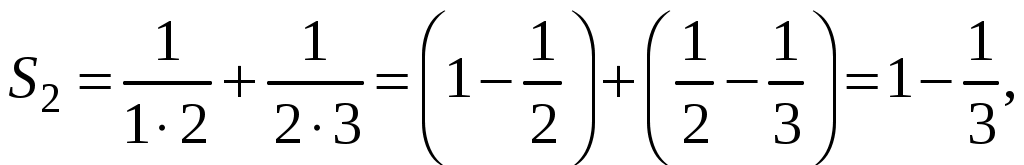 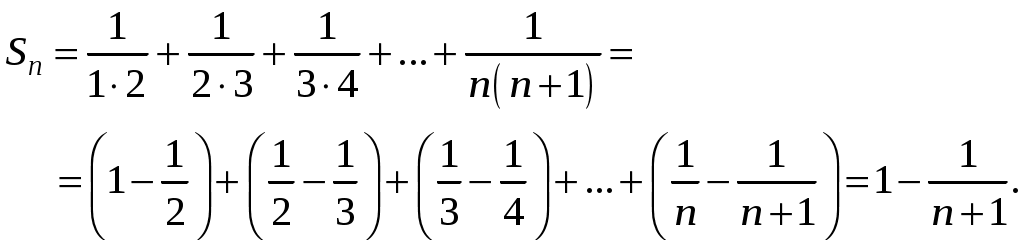 Следовательно, 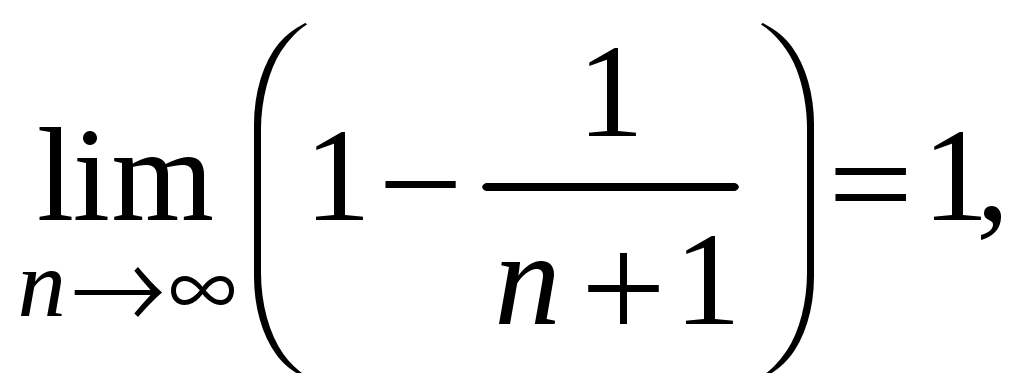 т. е. ряд сходится, его сумма равна 1. Рассмотри некоторые важные свойства рядов. Свойство 1. Если ряд (1) сходится и его сумма равна S, то ряд 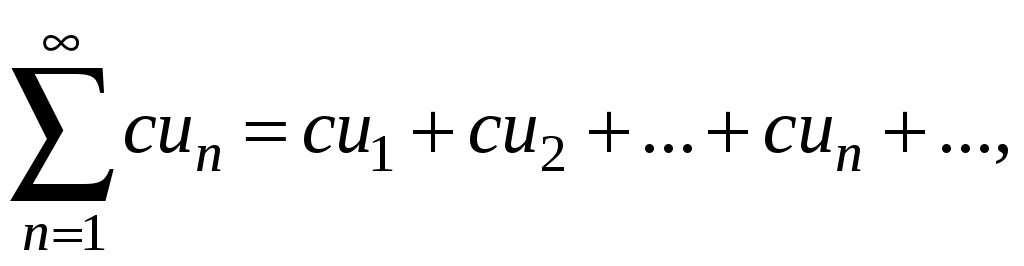 (2) (2)где с – произвольное число, также сходится и его сумма равна Обозначим n-ю частичную сумму ряда (2) через Следовательно, т. е. ряд (2) сходится и имеет сумму сS. Покажем теперь, что если ряд (1) расходится, Отсюда получаем: т. е. ряд (1) сходится, что противоречит условию о расходимости ряда (1). Свойство 2. Если сходится ряд (1) и сходится ряд 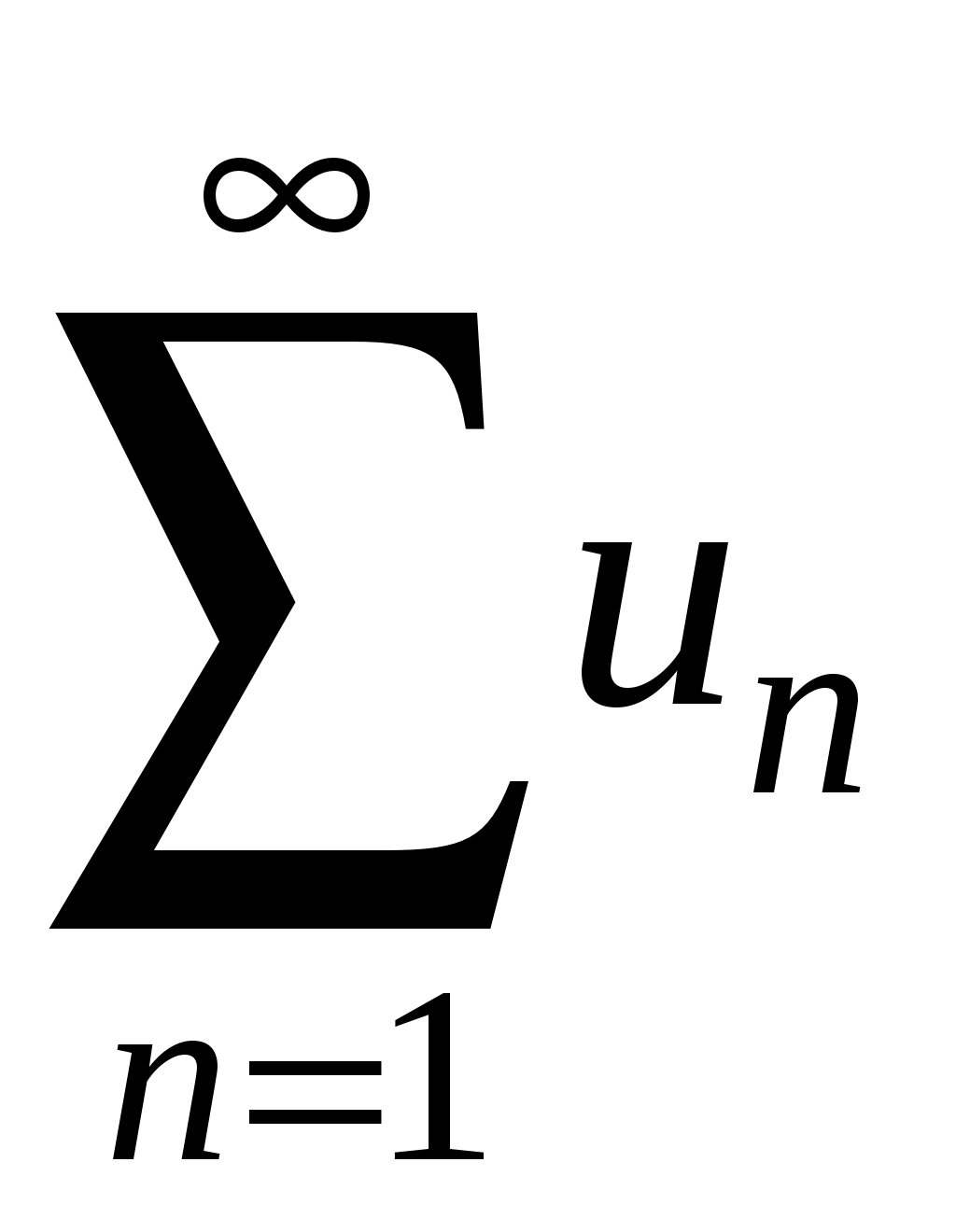 , (3) , (3)а их суммы равны 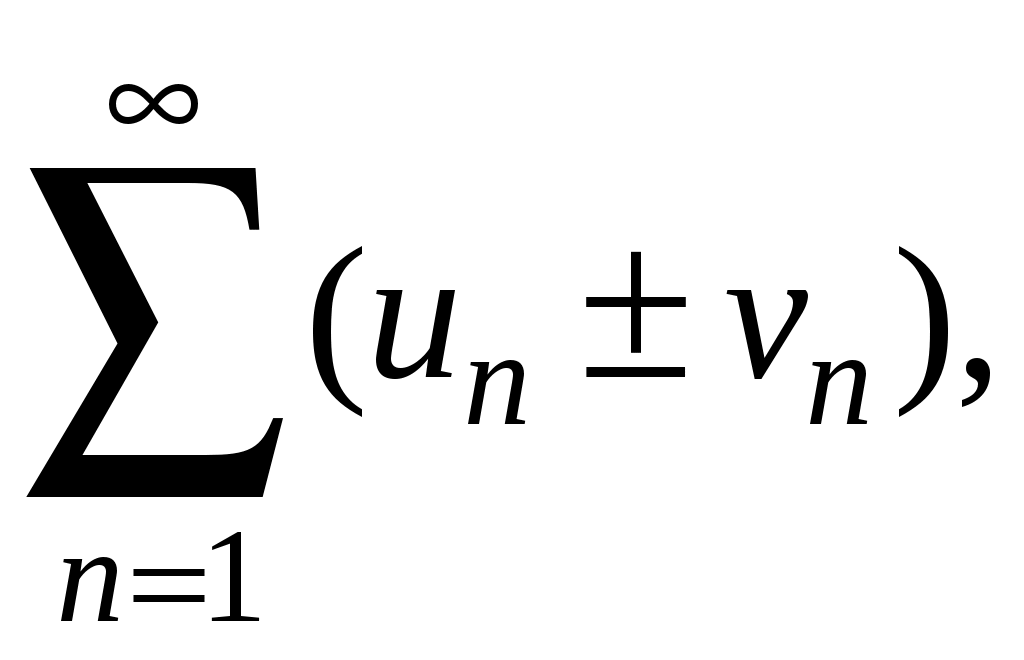 (4) (4)причем сумма каждого равна соответственно Обозначим n-е частичные суммы рядов (1), (3) и (4) через т. е. каждый из рядов (4) сходится, и сумма его равна Из свойства 1 вытекает, что сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд. В справедливости этого утверждения можно убедиться методом от противного. Заметим, что сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом. Свойство 3. Если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно. 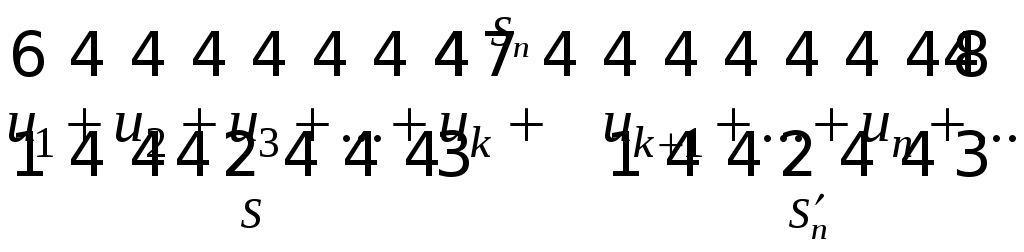 Обозначим через S сумму отброшенных членов, через k – наибольший из номеров этих членов. Чтобы не менять нумерацию оставшихся членов ряда (1), будем считать, что на месте отброшенных членов поставили нули. Тогда при Аналогично рассуждаем в случае приписывания к ряду конечного числа членов. Ряд 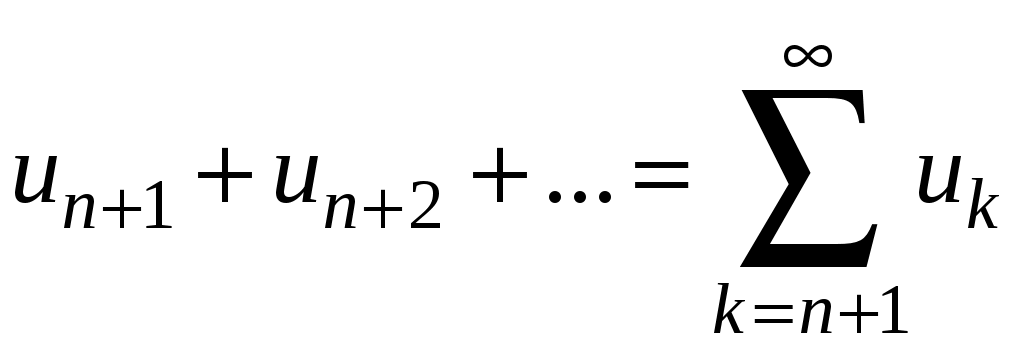 (5) (5)называется n-м остатком ряда (1). Он получается из ряда (1) отбрасыванием nпервых его членов. Ряд (1) получается из остатка добавлением конечного числа членов. Поэтому, согласно свойству 3, ряд (1) и его остаток (5) одновременно сходятся или расходятся. Из свойства 3 также следует, что если ряд (1) сходится, то его остаток Ряд геометрической прогрессии Исследуем сходимость ряда который называется рядом геометрической прогрессии. Ряд (6) часто используется при исследовании рядов на сходимость. Как известно, сумма первых nчленов прогрессии находится по формуле 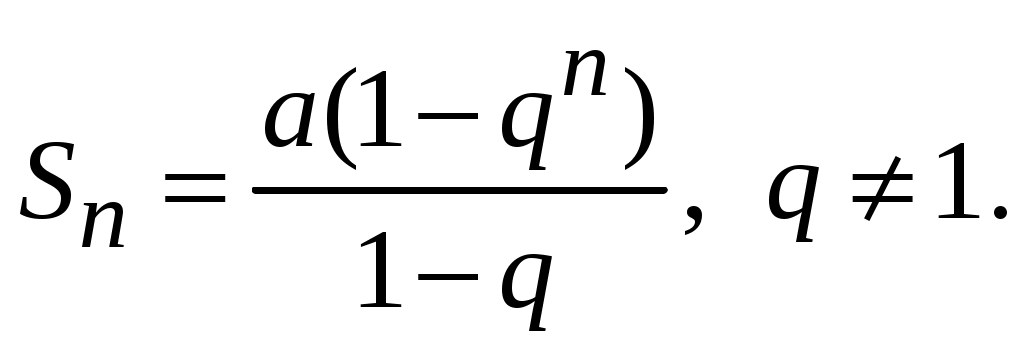 Найдем предел этой суммы Найдем предел этой суммы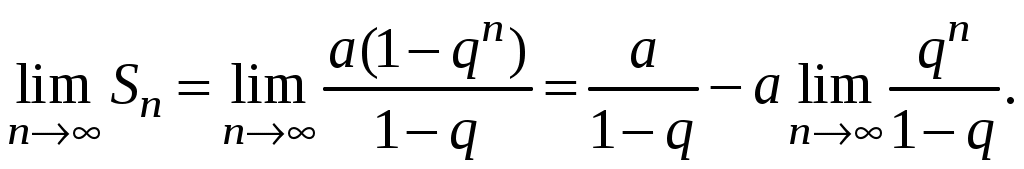 Рассмотрим следующие случаи в зависимости от величины q: 1. Если 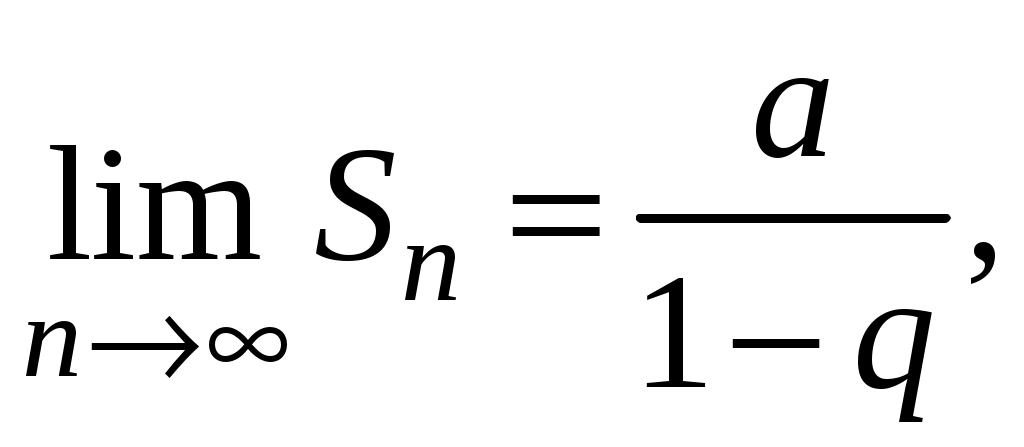 ряд (6) сходится, его сумма равна ряд (6) сходится, его сумма равна 2. Если 3. Если Итак, ряд геометрической прогрессии сходится при Пример 1. Показать, что ряд Решение: Данный ряд можно переписать так: Как видно, он представляет собой ряд геометрической прогрессии с Необходимый признак сходимости числового ряда. Гармонический ряд Нахождение n-ой частичной суммы Теорема 1. Если ряд (1) сходится, то его общий член Доказательство: Пусть ряд (1) сходится и Следствие 1 (достаточное условие расходимости ряда). Если Действительно, если бы ряд сходился, то (по теореме) Пример 2. Исследовать сходимость ряда 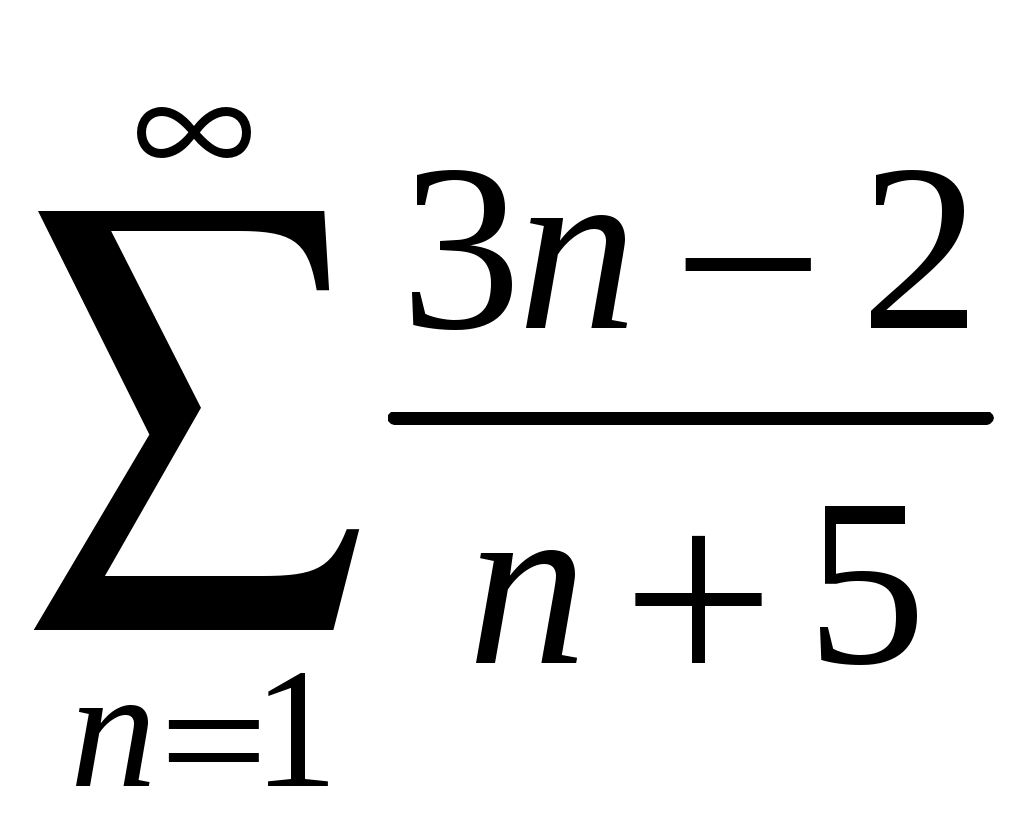 . .Решение: Ряд 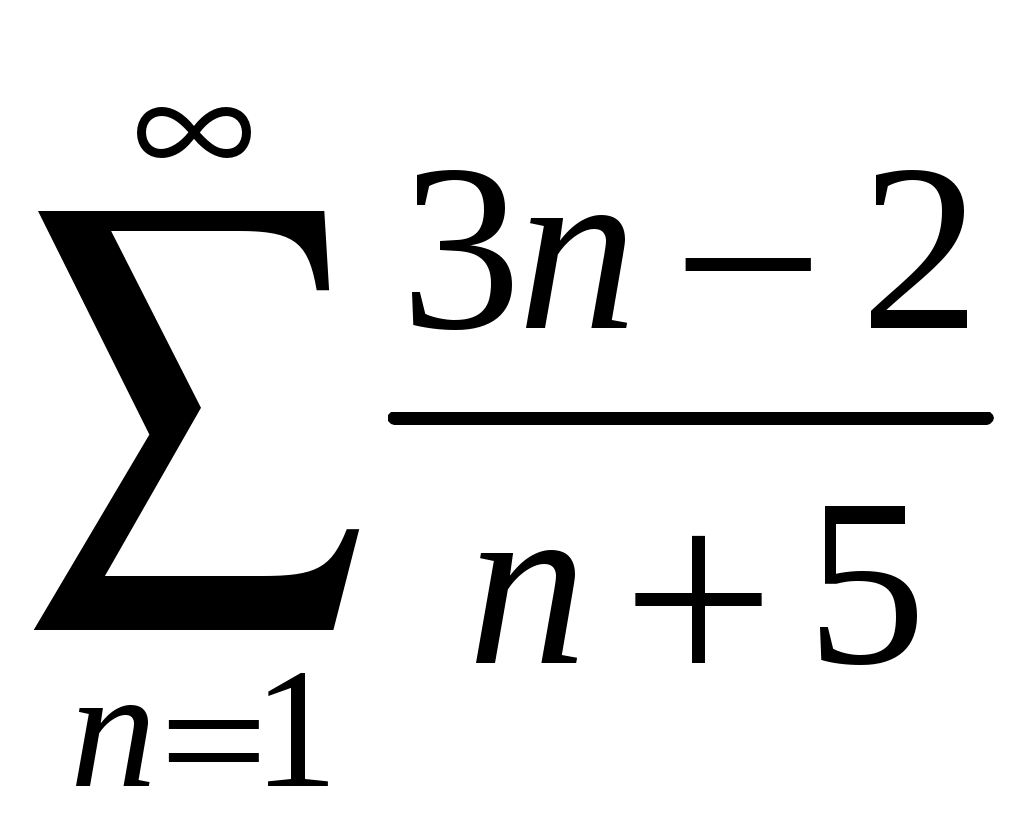 расходится, так как расходится, так какт. е. выполняется достаточное условие расходимости ряда. Пример 3. Исследовать сходимость ряда 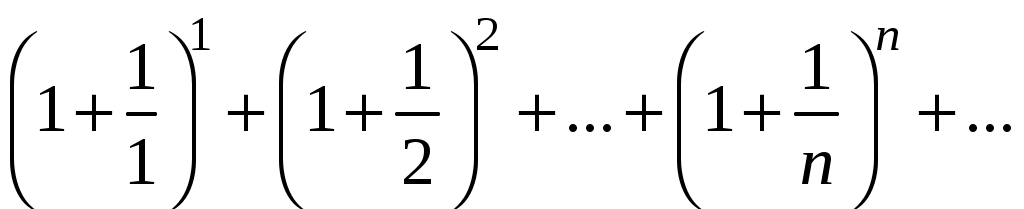 . .Решение: Данный ряд расходится, 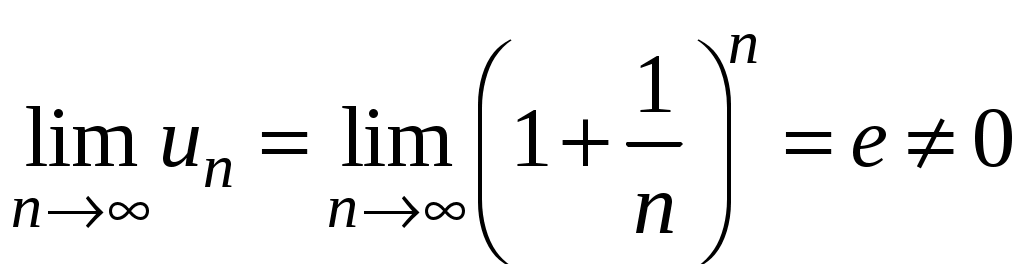 . .Теорема 1 дает необходимое условие сходимости ряда, но не достаточное: из условия В качестве примера рассмотрим так называемый гармонический ряд 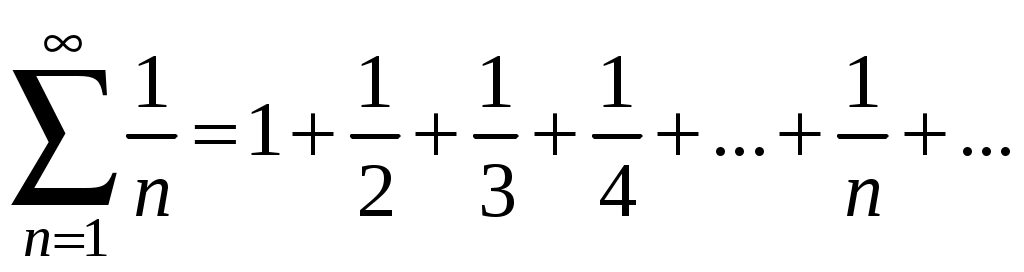 . (7) . (7)Очевидно, что Как известно, 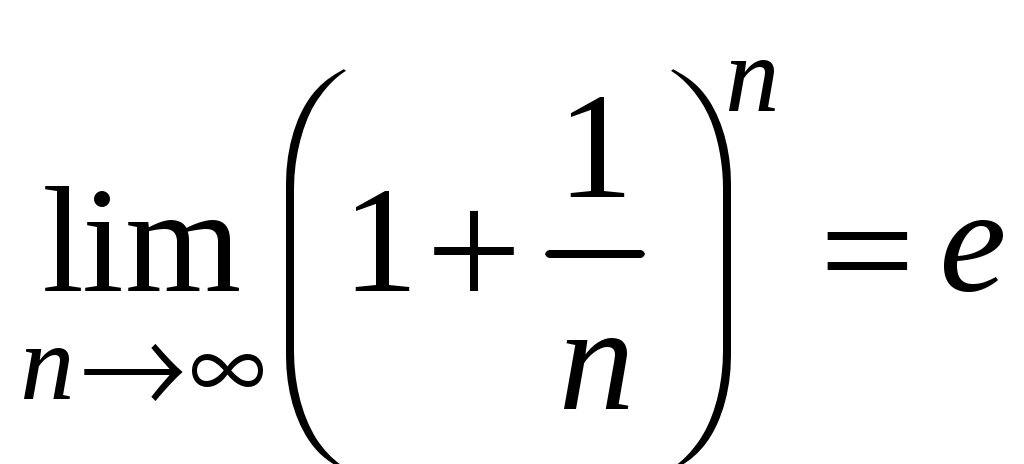 . Отсюда следует, что при любом . Отсюда следует, что при любом 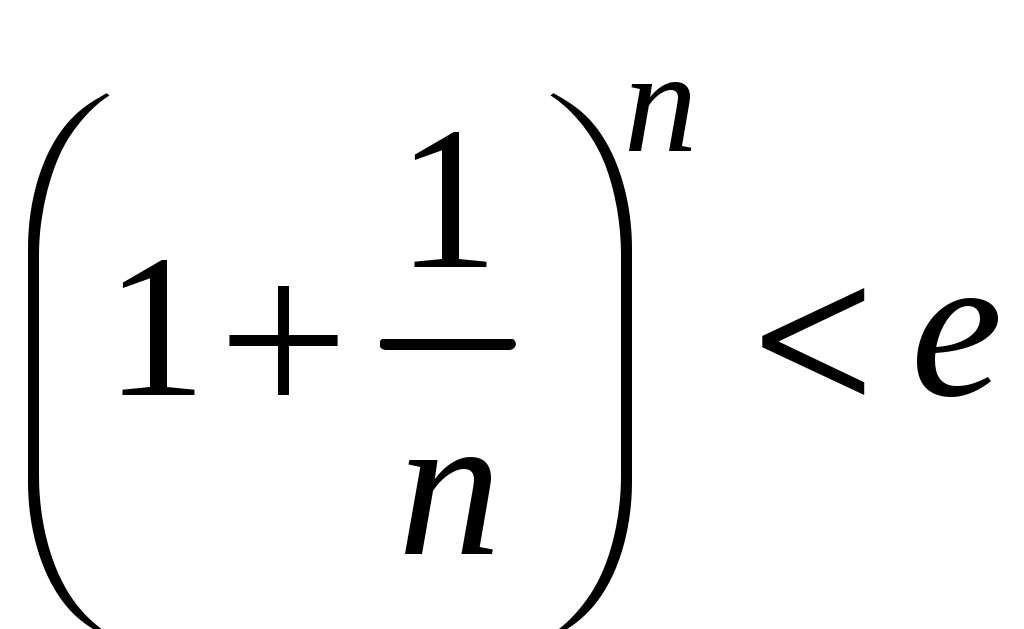 . Логарифмируя это неравенство по основанию е, получим: . Логарифмируя это неравенство по основанию е, получим: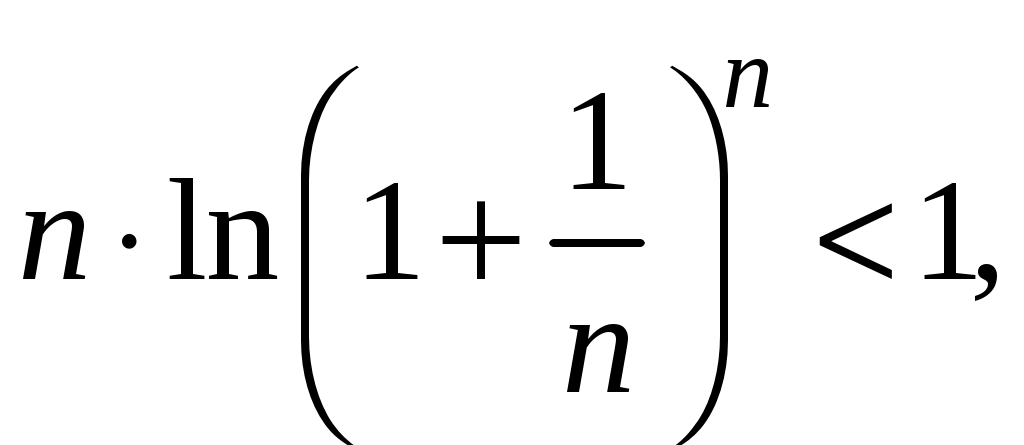 т. е. Подставляя в полученное неравенство поочередно n = 1, 2, …, n– 1, n, получим: 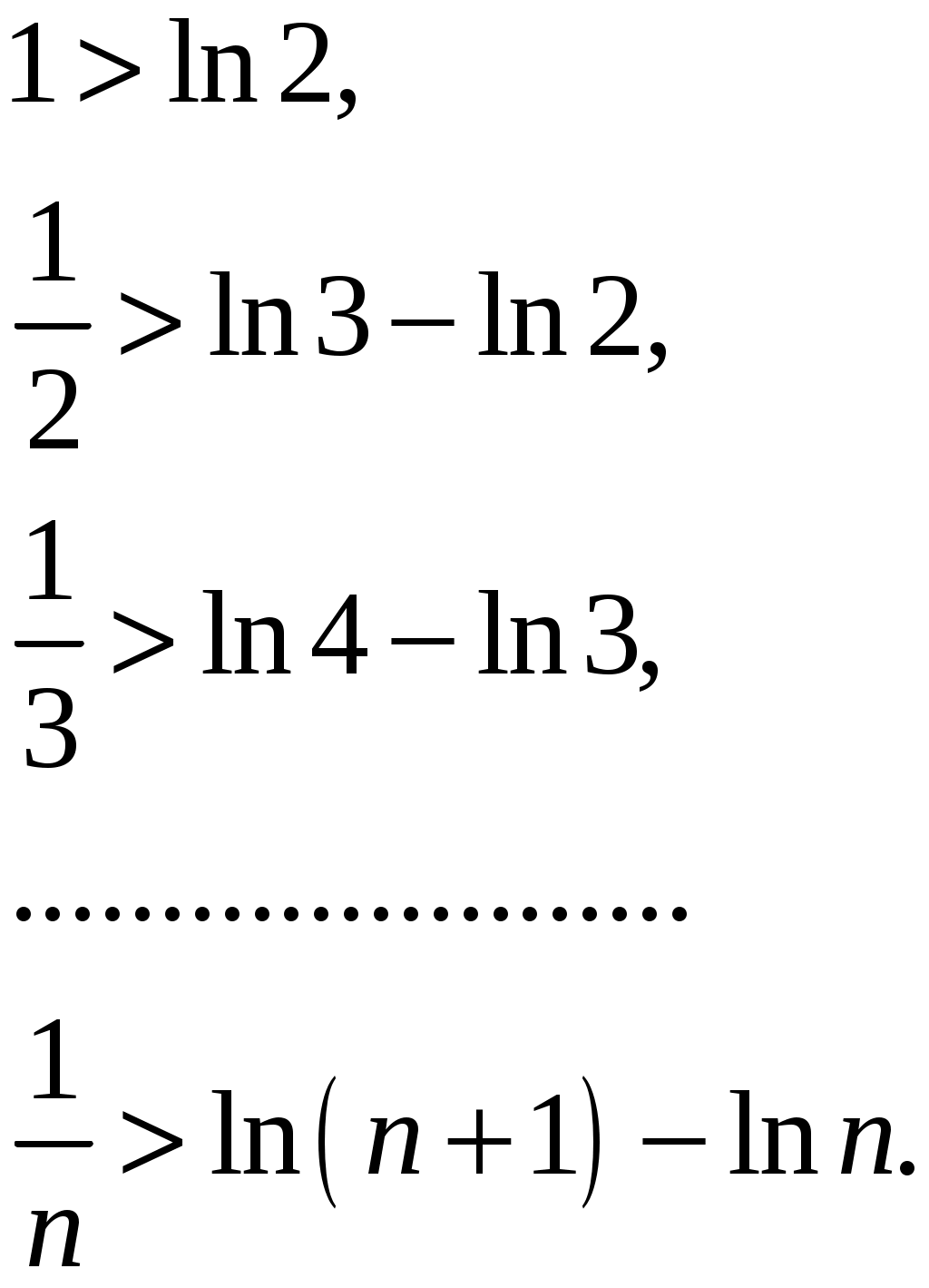 Сложив почленно эти неравенства, получим В качестве второго примера можно взять ряд 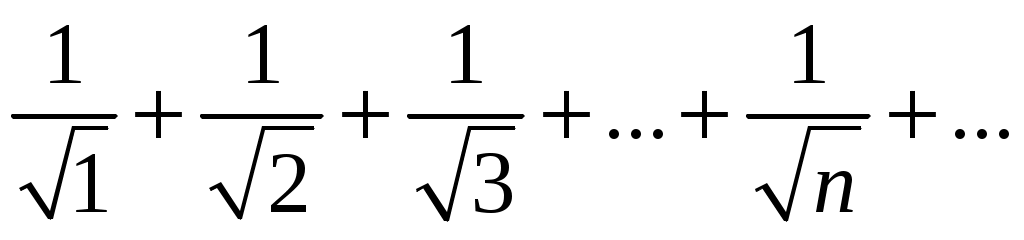 Здесь 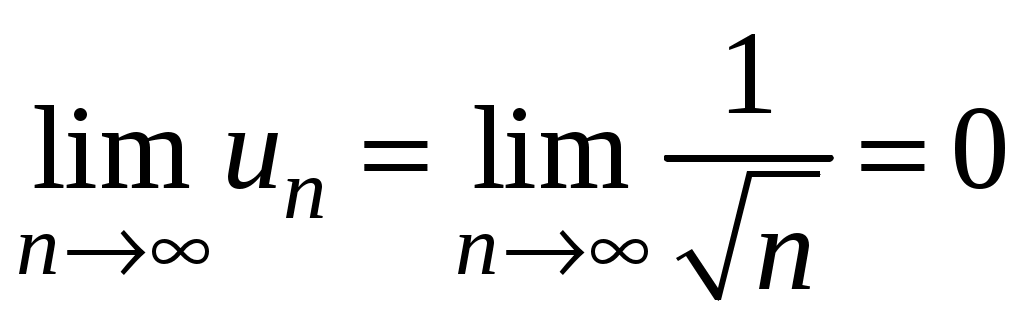 . Однако этот ряд расходится. . Однако этот ряд расходится.Действительно, 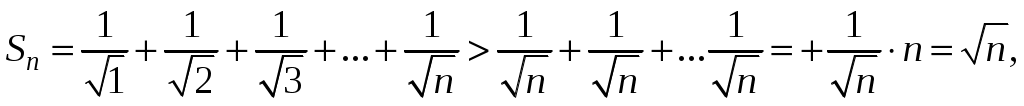 т. е. |
