Ряды. Ряды. Основные понятия
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
|
Знакочередующиеся ряды. Признак Лейбница Рассмотрим важный класс рядов, называемых знакочередующимися. Знакочередующимся рядом называется ряд вида 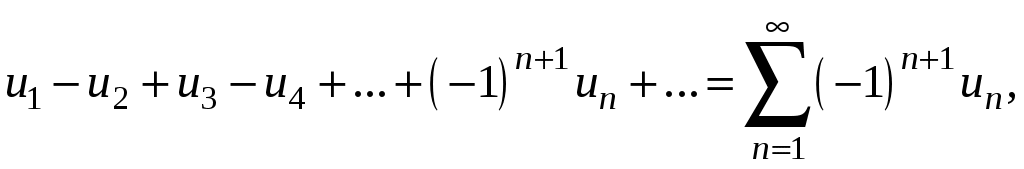 (1) (1)где Для знакочередующихся рядов имеет место достаточный признак сходимости (установленный в 1714 г. Лейбницем в письме к И. Бернулли). Теорема 1 (признак Лейбница). Знакочередующийся ряд (1) сходится, если: 1). Последовательность абсолютных величин членов ряда монотонно убывает, т. е. 2). Общий член ряда стремится к нулю: Рассмотрим сначала частичную сумму четного числа Выражение в каждой скобке, согласно первому условию теоремы, положительно. Следовательно, сумма С другой стороны, Легко видеть, что Рассмотрим теперь частичные суммы нечетного числа т. к. Вывод: Итак, Замечания. Исследование знакочередующегося ряда вида (с отрицательным первым членом) сводится путем умножения всех его членов на (–1) к исследованию ряда (1). 2. Соотношение (2) позволяет получить простую и удобную оценку ошибки, которую мы допускаем, заменяя сумму S данного ряда его частичной суммой Sn. Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд Ряды (1) и (3), для которых выполняются условия теоремы Лейбница, называются лейбницевскими (или рядами Лейбница). Пример 1. Вычислить приблизительную сумму ряда 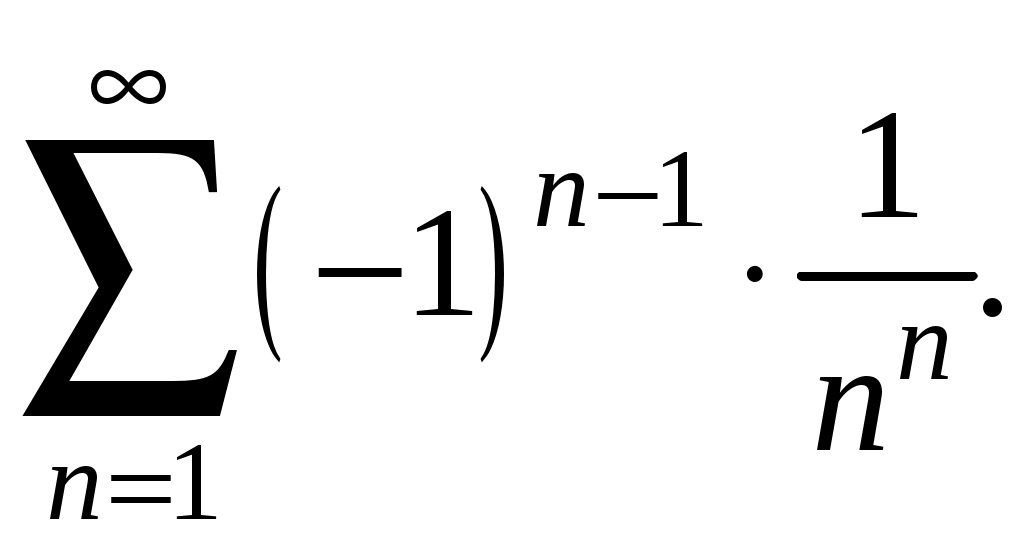 Решение. Данный ряд лейбницевского типа. Он сходится. Можно записать: сделаем ошибку, меньшую, чем Общий достаточный признак сходимости знакопеременных рядов Знакочередующийся ряд является частным случаем знакопеременного ряда. Числовой ряд 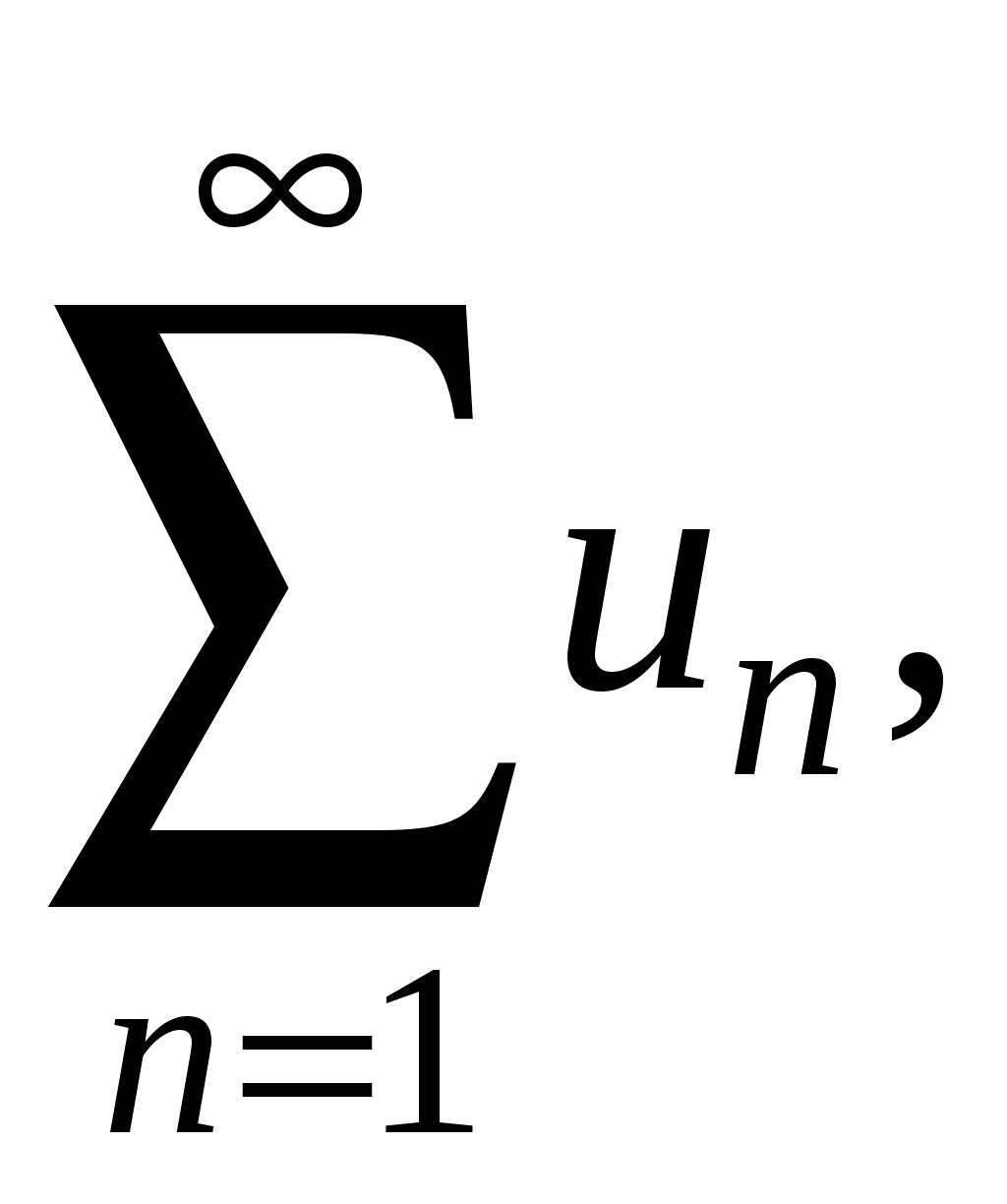 содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости. Теорема 2. Пусть дан знакопеременный ряд Если сходится ряд составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд (4). Рассмотрим вспомогательный ряд, составленный из членов рядов (4) и (5): 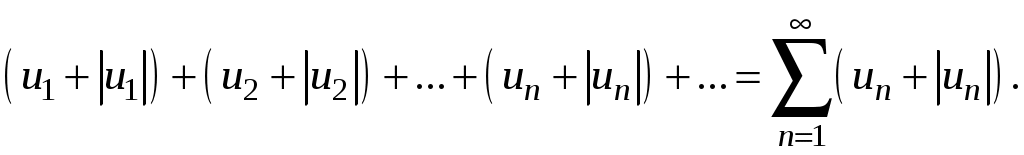 Очевидно, что 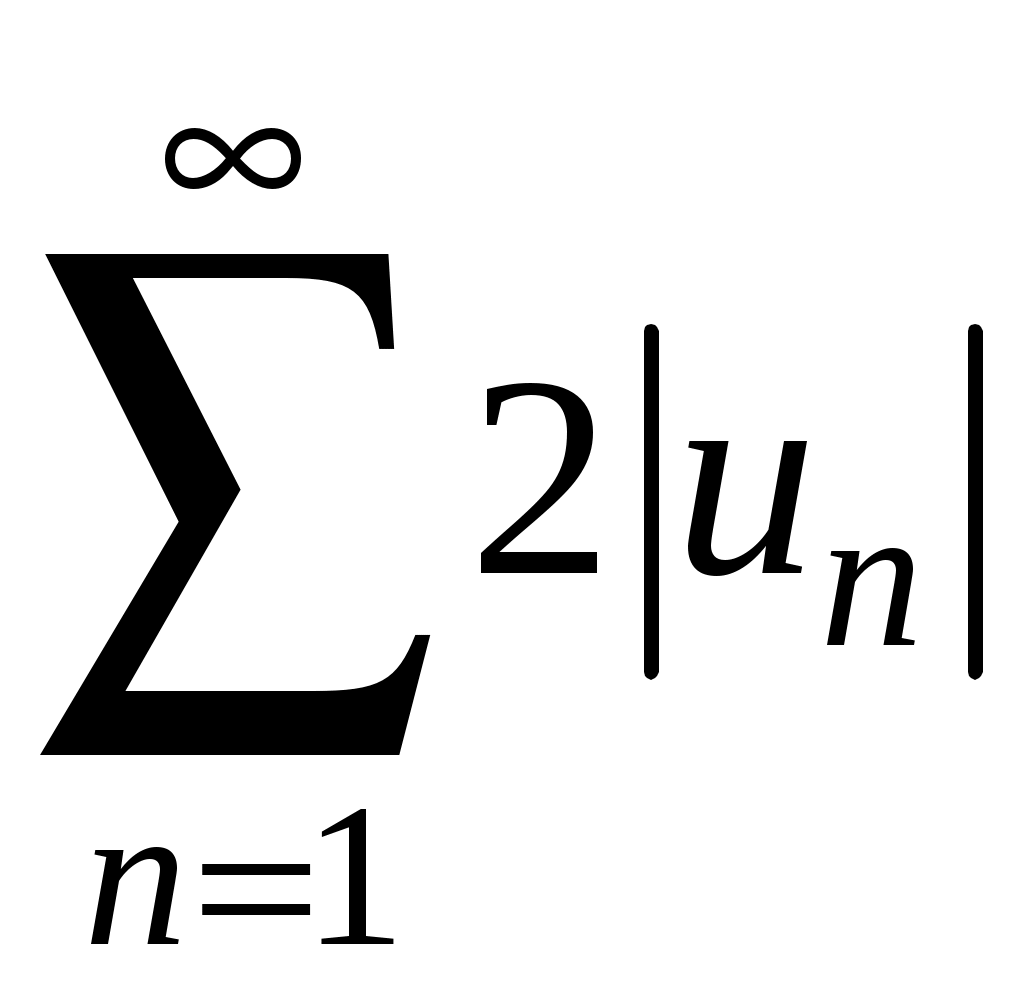 сходится в силу условия теоремы и свойства 1 числовых рядов. Следовательно, на основании признака сравнения сходится и ряд сходится в силу условия теоремы и свойства 1 числовых рядов. Следовательно, на основании признака сравнения сходится и ряд 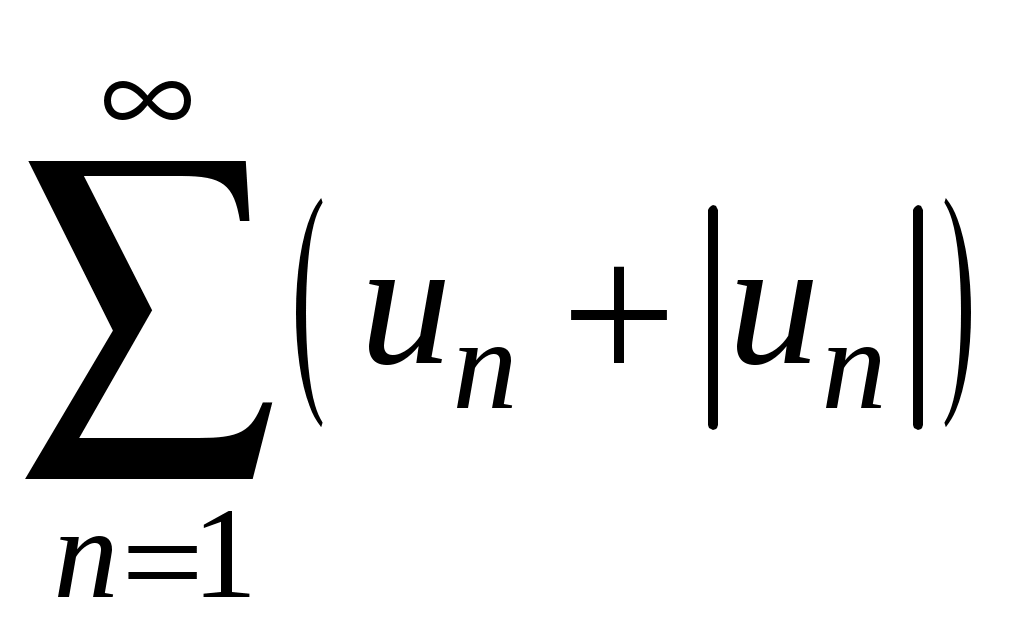 . Поскольку данный знакопеременный ряд (4) представляет собой разность двух сходящихся рядов . Поскольку данный знакопеременный ряд (4) представляет собой разность двух сходящихся рядов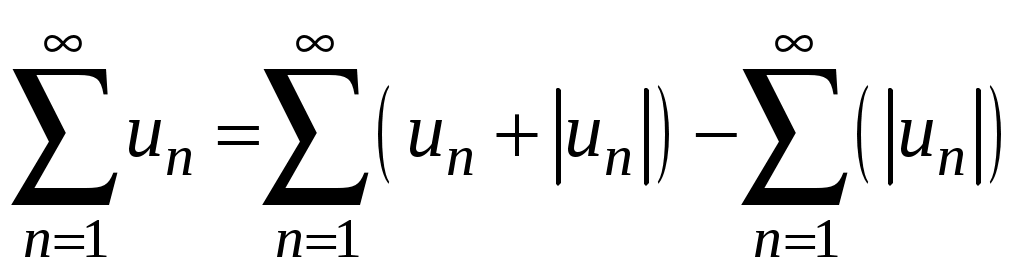 , ,то, на основании свойства 2 числовых рядов, ряд (4) сходится. Отметим, что обратное утверждение несправедливо: если ряд сходится ряд (4), то это не означает, что будет сходиться ряд (5). Пример 2. Исследовать сходимость ряда 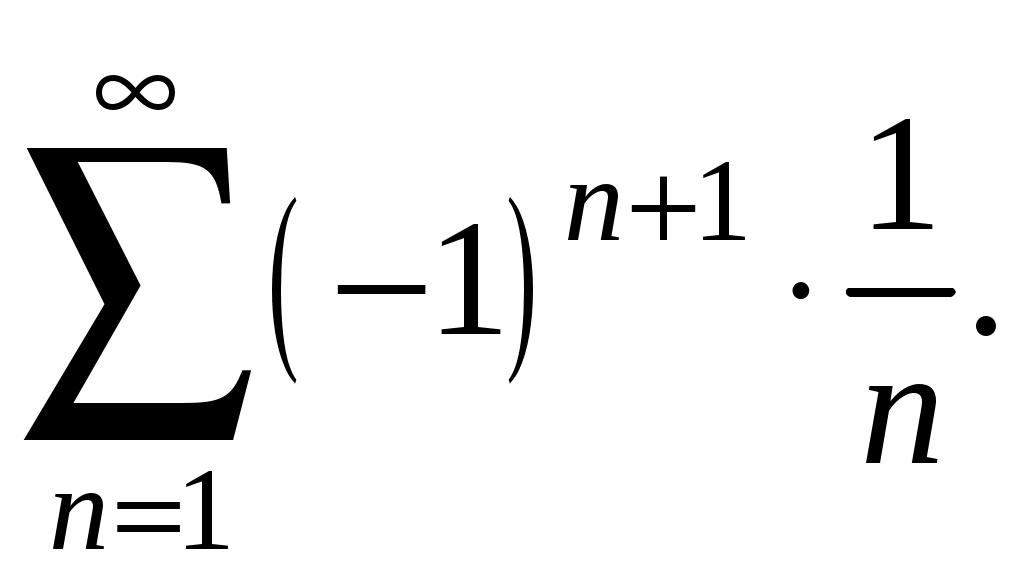 Решение. Это знакочередующийся ряд, для которого выполнены условия признака Лейбница. Следовательно, указанный ряд сходится. Однако ряд, составленный из модулей членов данного ряда, т. е. ряд 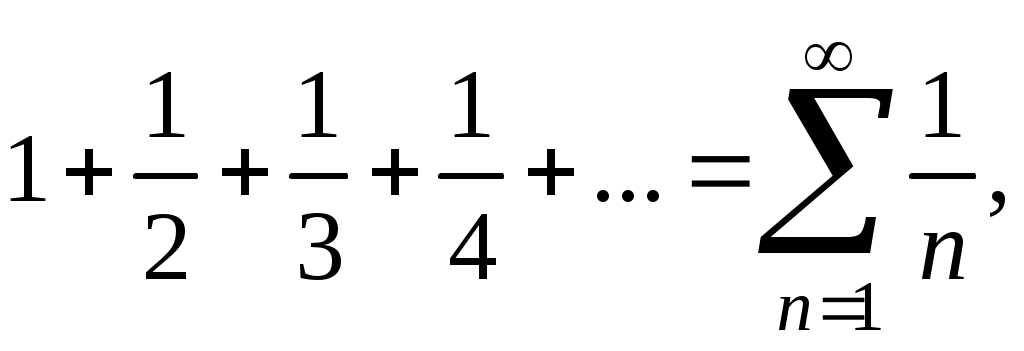 расходится (гармонический ряд). Абсолютная и условная сходимости числовых рядов Знакопеременный ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится. Так, ряд, показанный в примере 2, условно сходящийся. Ряд 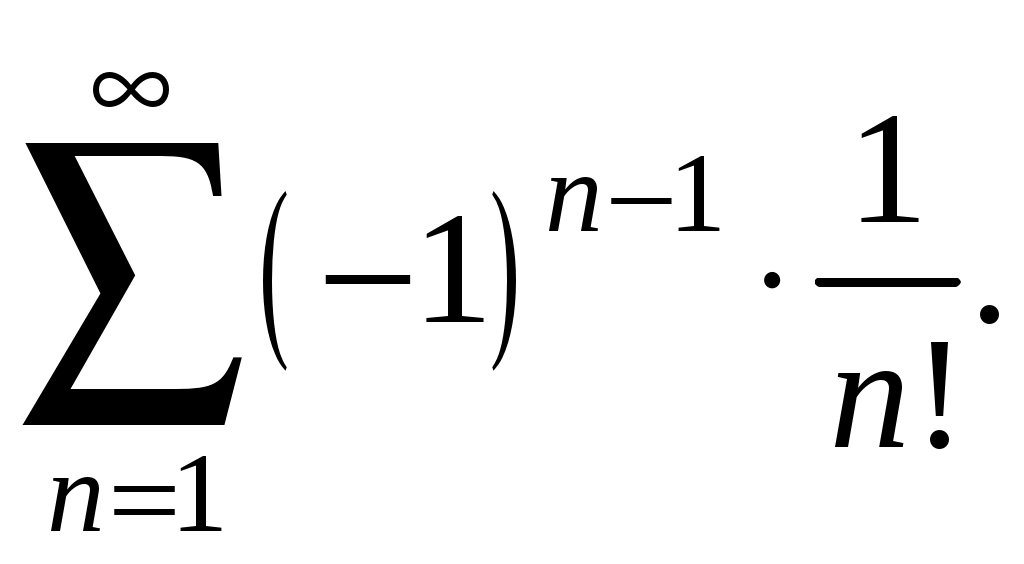 абсолютно сходится, т. к. ряд, составленный из модулей его членов, сходится. Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм (переместительность, сочетательность, распределительность). Основные свойства абсолютно сходящихся рядов приводим без доказательства. 1. Если ряд абсолютно сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S, что и исходный ряд (теорема Дирихле). 2. Абсолютно сходящиеся ряды с суммами S1 и S2 можно почленно складывать (вычитать). В результате получается абсолютно сходящийся ряд, сумма которого равна 3. Под произведением двух рядов 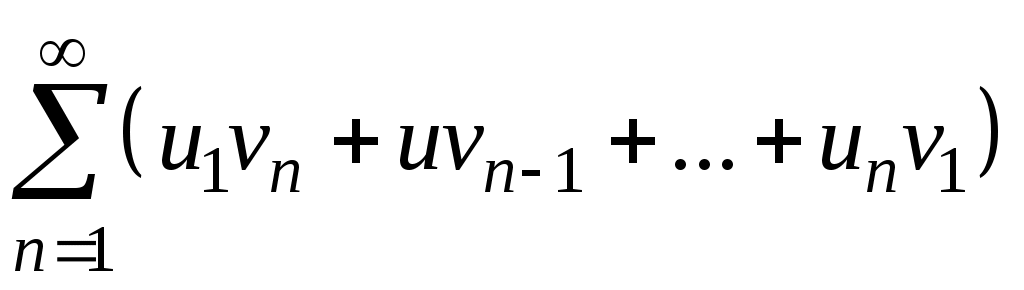 Произведение двух абсолютно сходящихся рядов с суммами S1 и S2 есть абсолютно сходящийся ряд, сумма которого равна S1· S2. Таким образом, абсолютно сходящиеся ряды суммируются, вычитаются, перемножаются как обычные ряды. Суммы таких рядов не зависят от порядка записи членов. В случае условно сходящихся рядов соответствующие утверждения (свойства), вообще говоря, не имеют места. Так, переставляя члены условно сходящегося ряда, можно добиться того, что сумма ряда изменится. Например, ряд 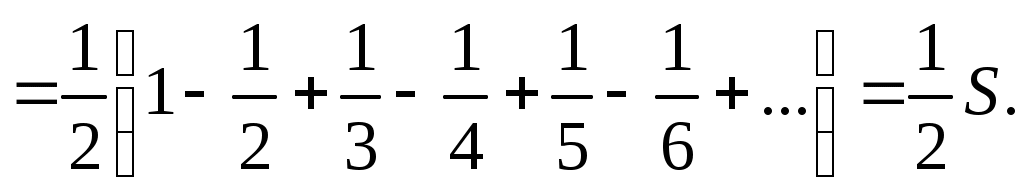 Сумма уменьшилась вдвое. Более того, путем перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее заданной суммой или расходящийся ряд (теорема Римана). Поэтому действия над рядами нельзя производить, не убедившись в их абсолютной сходимости. Для установления абсолютной сходимости используют все признаки сходимости знакоположительных рядов, заменяя всюду общий член ряда его модулем. Функциональные ряды. Основные понятия Ряд, членами которого являются функции от х, называется функциональным: 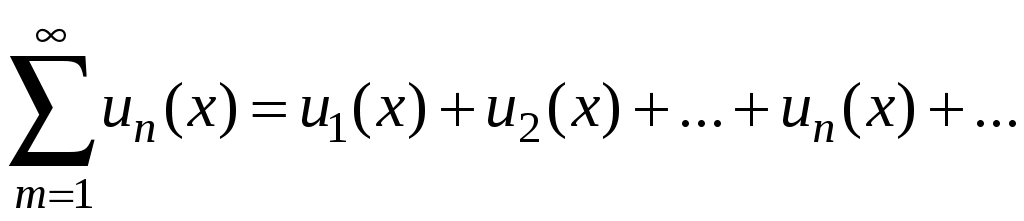 (1) (1)Придавая х определенное значение который может быть как сходящимся, так и расходящимся. Если полученный числовой ряд сходится, то точка Совокупность числовых значений аргумента х, при которых функциональный ряд сходится, называется его областью сходимости. В области сходимости функционального ряда его сумма является некоторой функцией от х: Пример 1. Найти область сходимости ряда 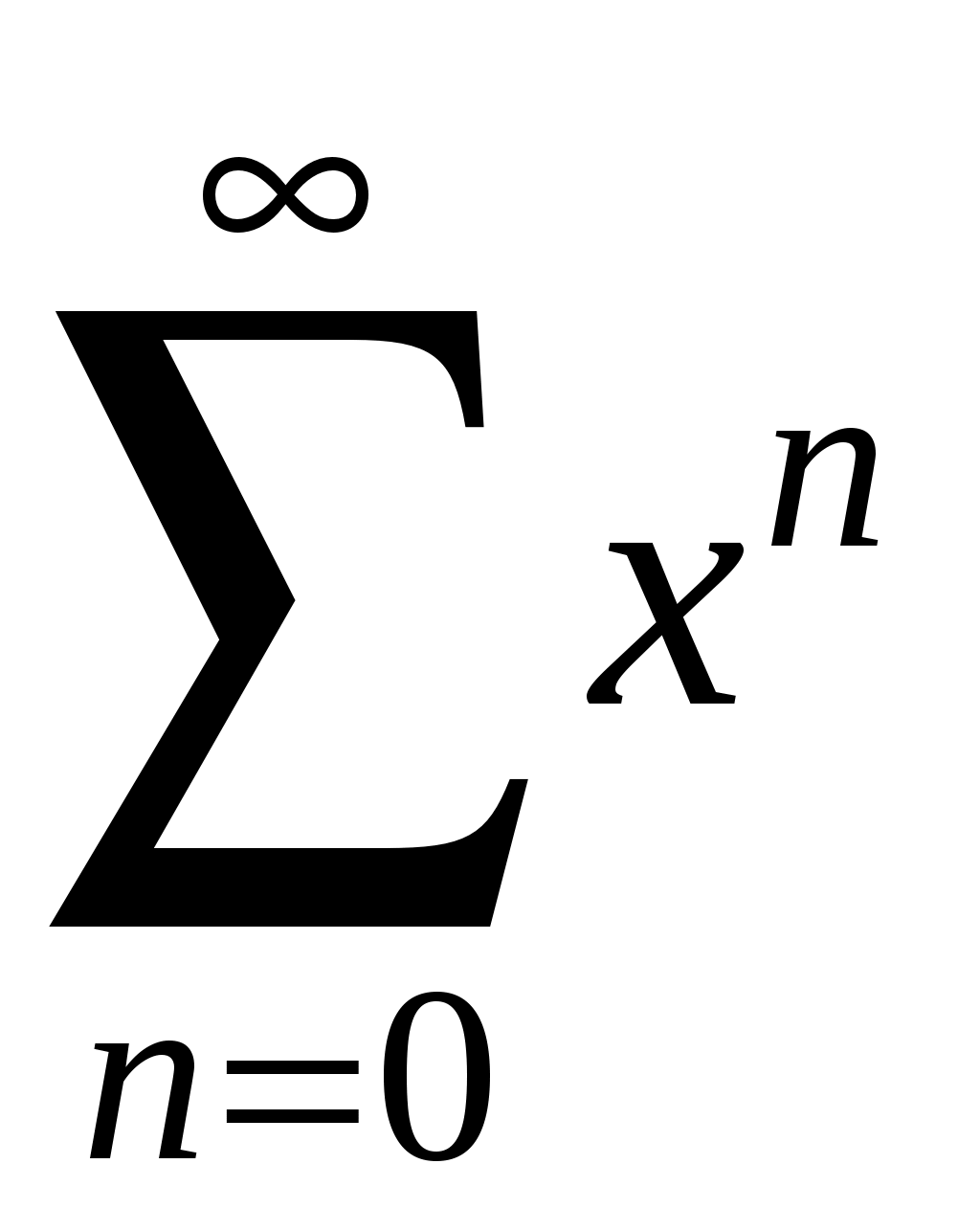 . .Решение. Данный ряд является рядом геометрической прогрессии со знаменателем 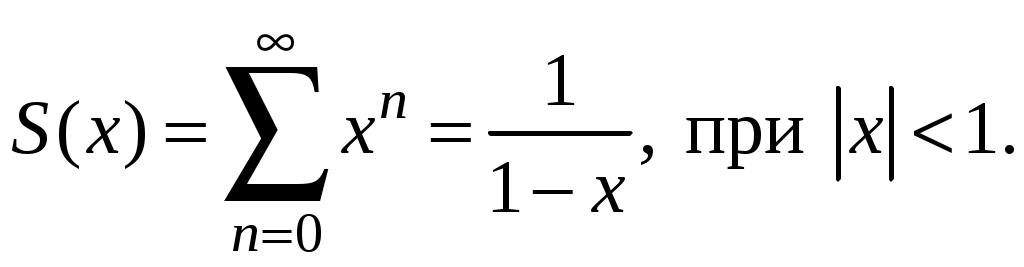 Пример 2. Исследовать сходимость функционального ряда 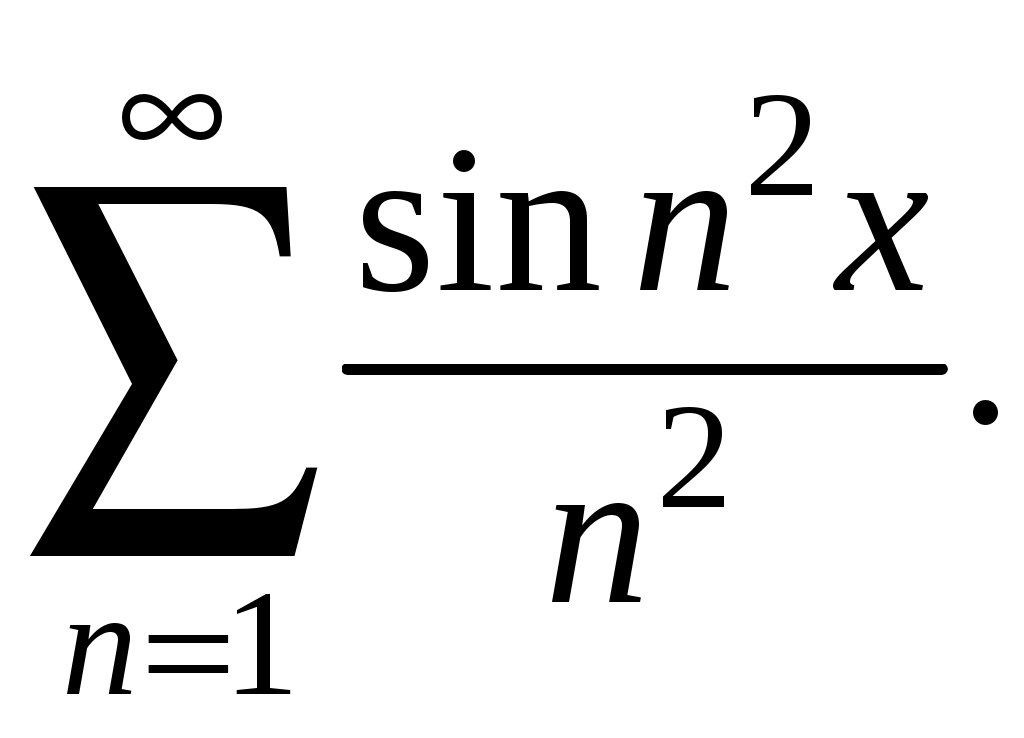 Решение. Составим ряд из абсолютных величин членов исходного ряда 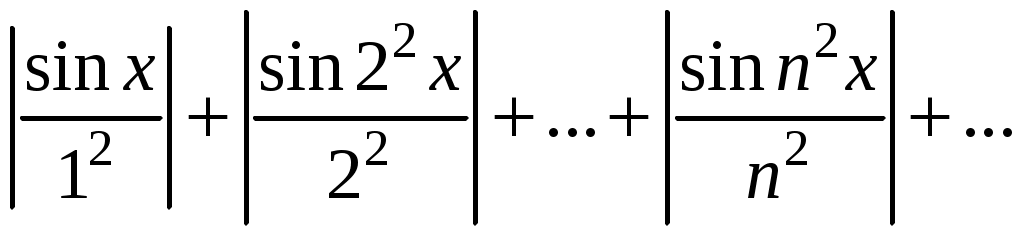 (2) (2)Так как при любом 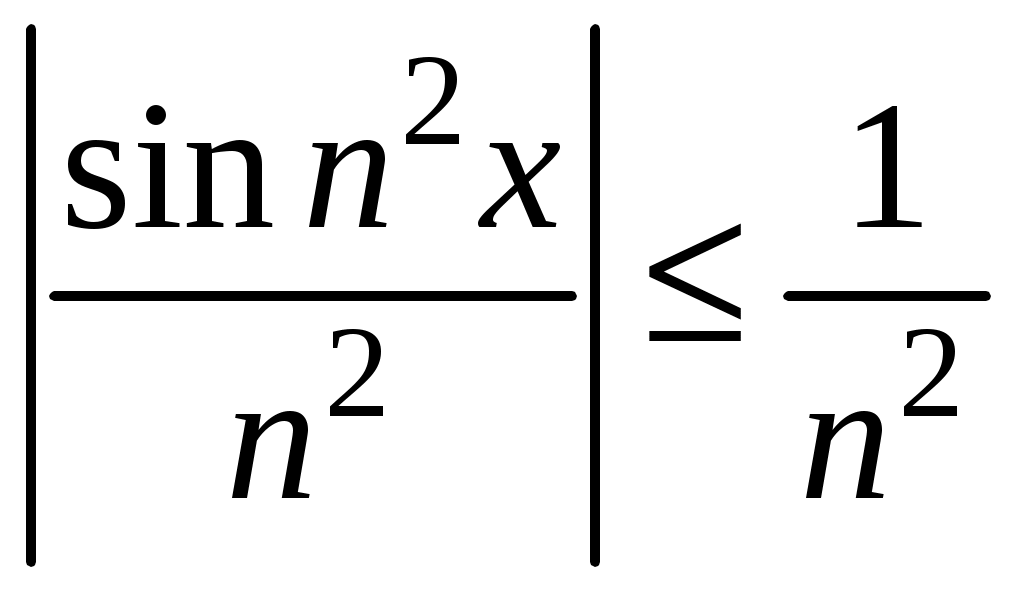 , а ряд с общим членом , а ряд с общим членом Среди функциональных рядов в математике и её приложениях особую роль играет ряд, членами которого являются степенные функции аргумента х, т. е. так называемый степенной ряд: 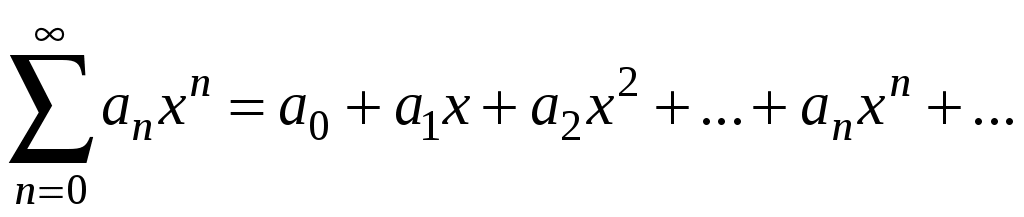 (3) (3)Действительные (или комплексные) числа Ряд (3) расположен по степеням х. Рассматривают также степенной ряд, расположенный по степеням 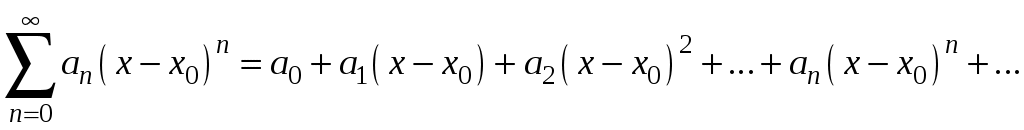 , (4) , (4)где Ряд (4) легко приводится к виду (3), если положить Сходимость степенных рядов Выясним вопрос о сходимости степенного ряда (3). Область сходимости степенного ряда (3) содержит по крайней мере одну точку: 2.1. Теорема Абеля Об области сходимости степенного ряда можно судить, исходя из следующей теоремы: Теорема 1 (Абель). Если степенной ряд (3) сходится при По условию ряд 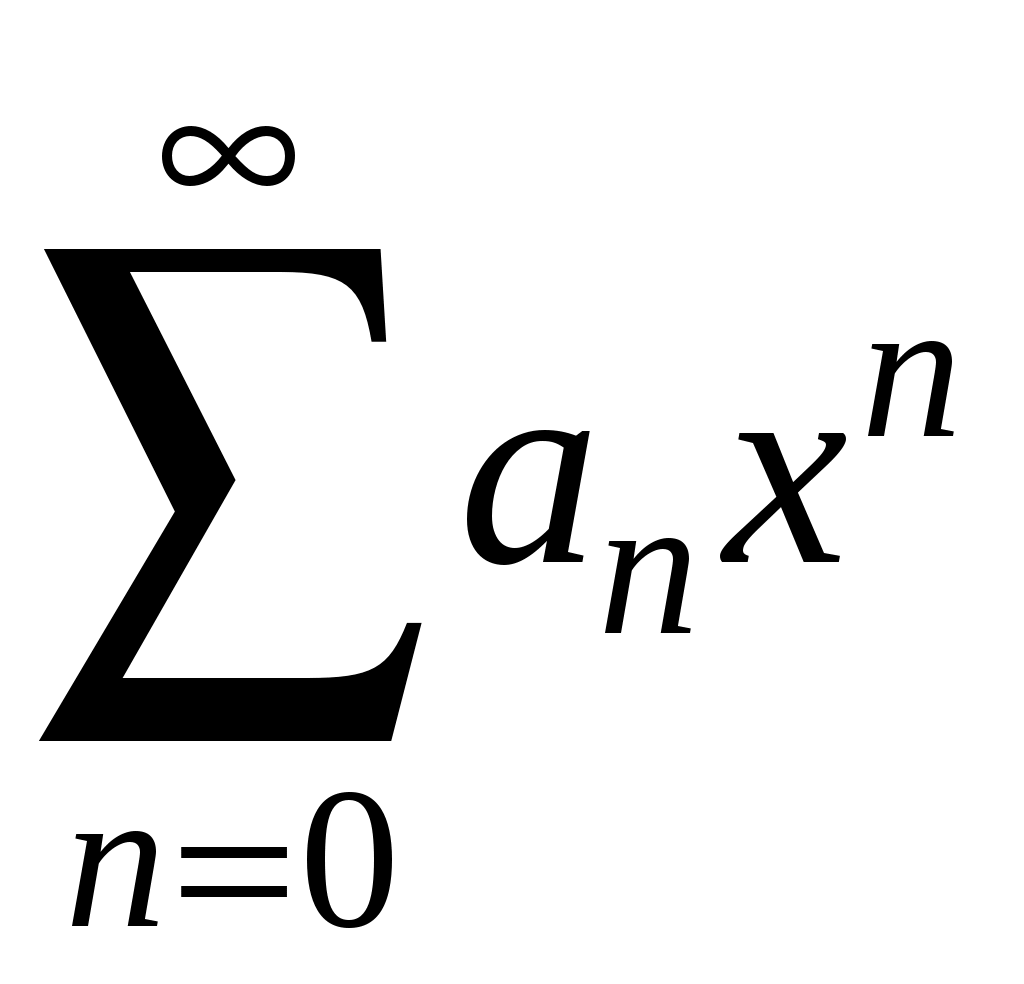 сходится. Следовательно, по необходимому признаку сходимости сходится. Следовательно, по необходимому признаку сходимости Пусть 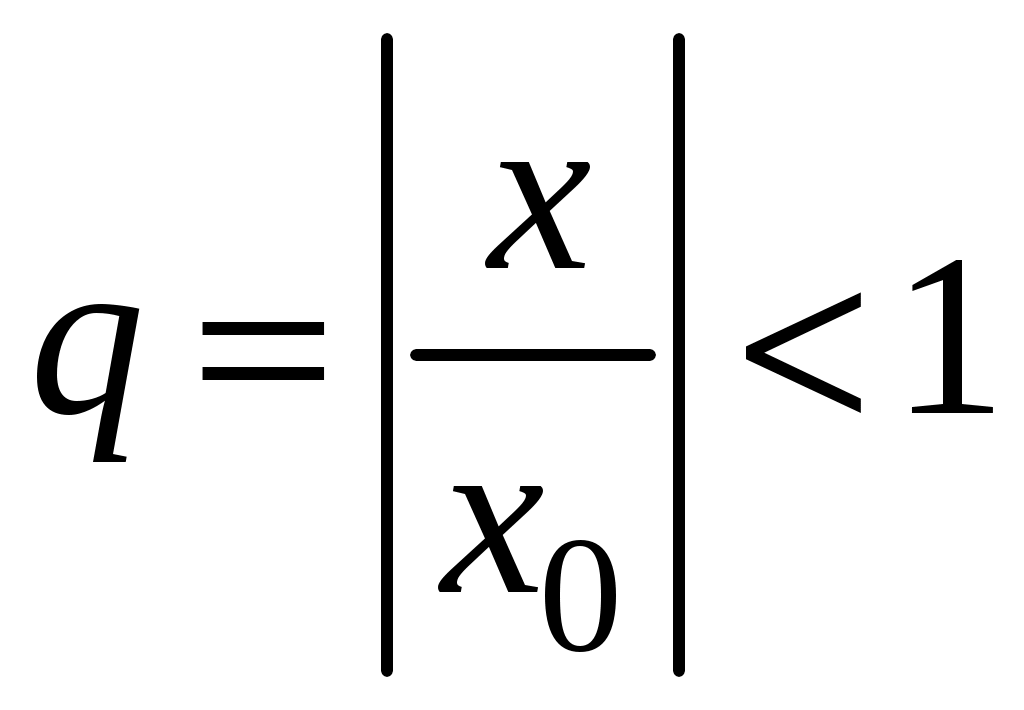 и, следовательно, и, следовательно,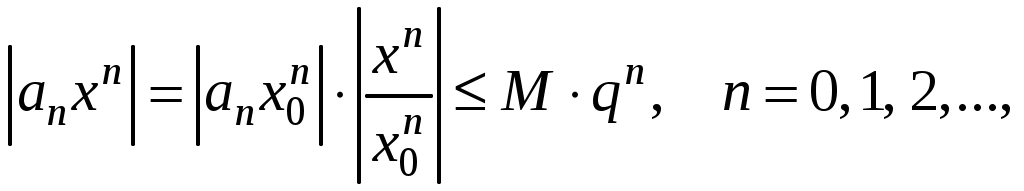 т. е. модуль каждого члена ряда (3) не превосходит соответствующего члена сходящегося Следствие 1. Если ряд (3) расходится при Действительно, если допустить сходимость ряда в точке Интервал и радиус сходимости степенного ряда Из теоремы Абеля следует, что если  Рис. 1 Интервал В частности, когда ряд (3) сходится лишь в одной точке Отметим, что на концах интервала сходимости (т. е. при Для нахождения радиуса сходимости степенного ряда (3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда и применим к нему признак Даламбера. Допустим, что существует предел 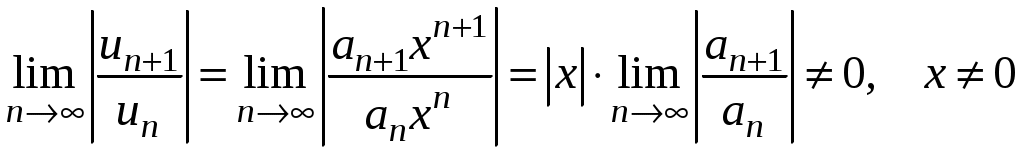 . .По признаку Даламбера ряд сходится, если 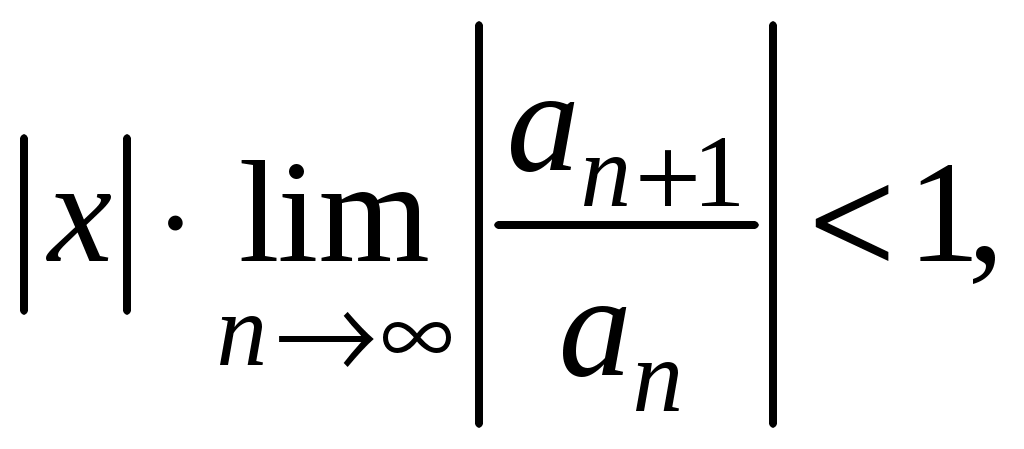 т. е. ряд сходится при тех значениях х, для которых т. е. ряд сходится при тех значениях х, для которых 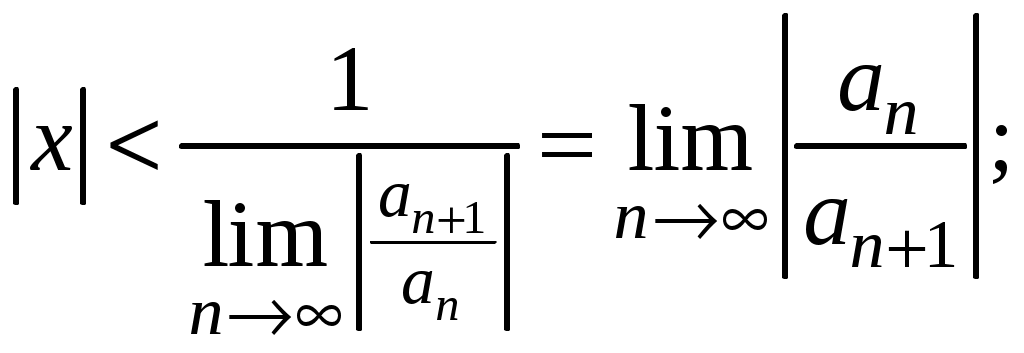 ряд, составленный из модулей членов ряда (3), расходится при тех значениях х, для которых 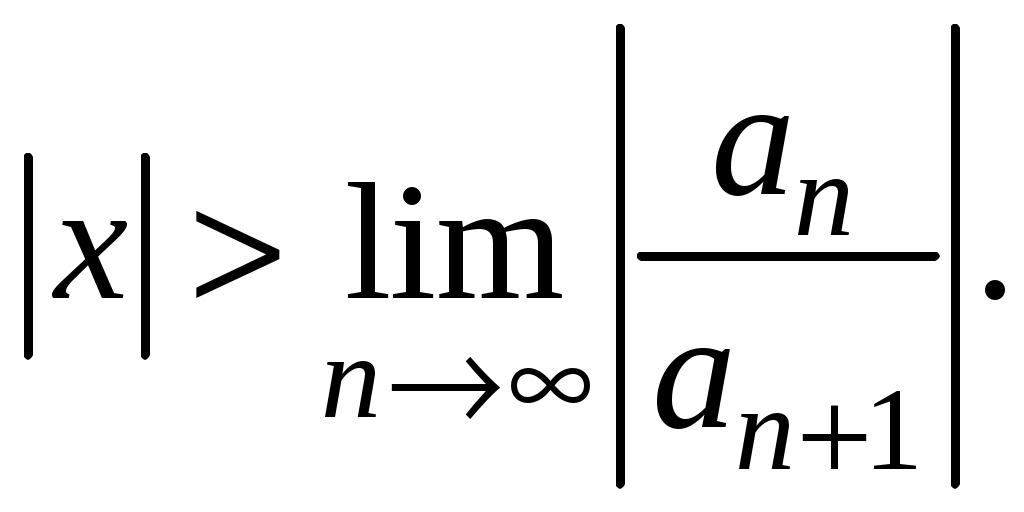 Таким образом, для ряда (3) радиус абсолютной сходимости Таким образом, для ряда (3) радиус абсолютной сходимости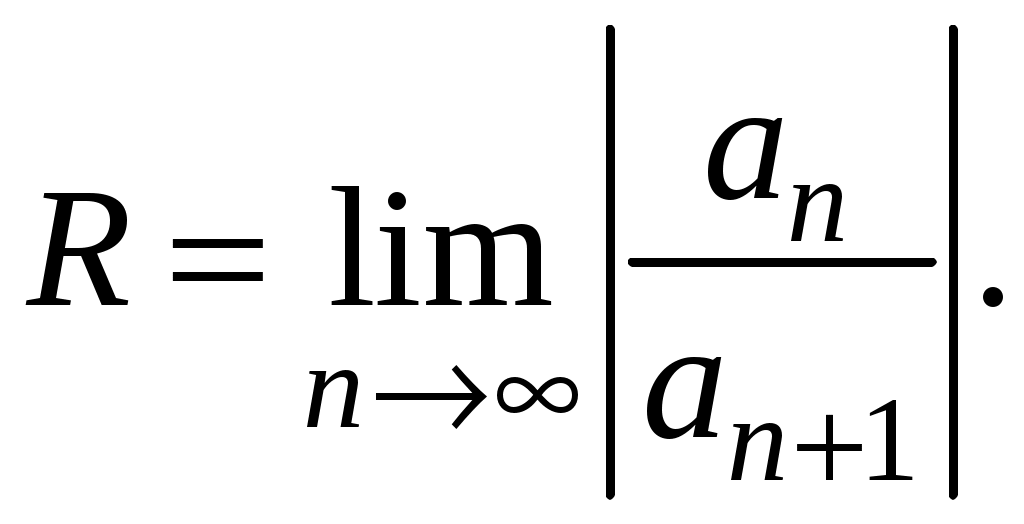 (5) (5)Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что 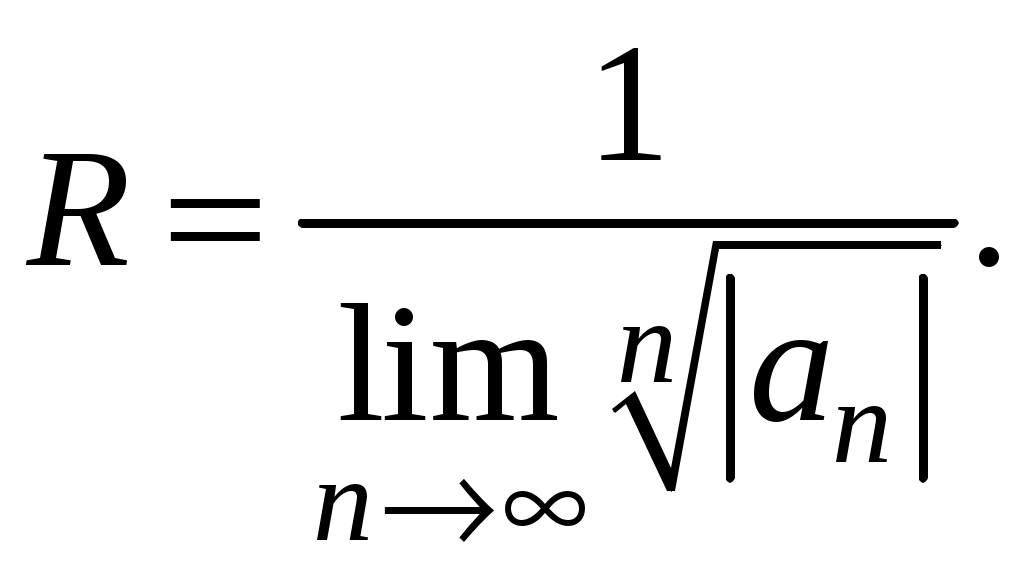 (6) (6)Замечания. 1.Если 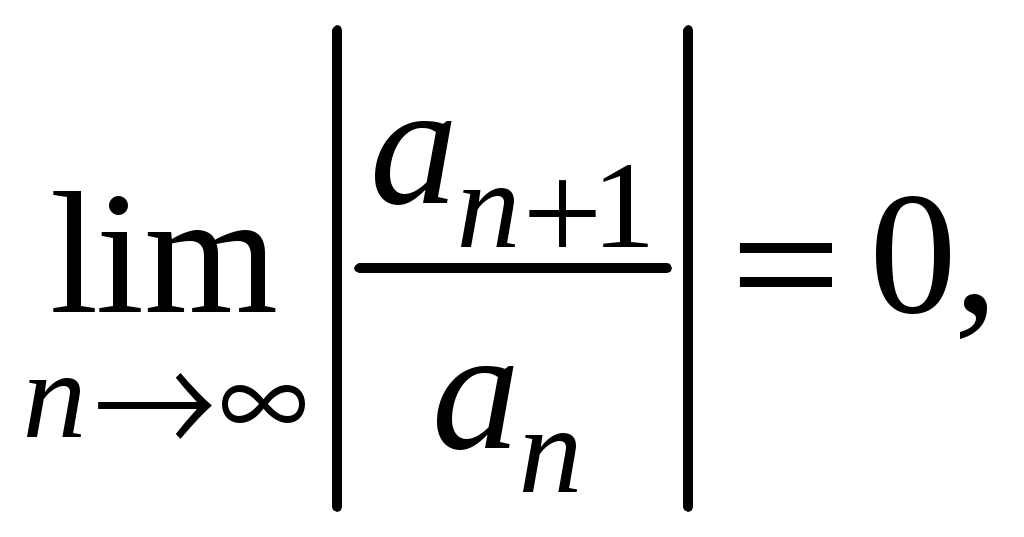 то можно убедиться, что ряд (3) абсолютно сходится на всей числовой оси. В этом случае то можно убедиться, что ряд (3) абсолютно сходится на всей числовой оси. В этом случае 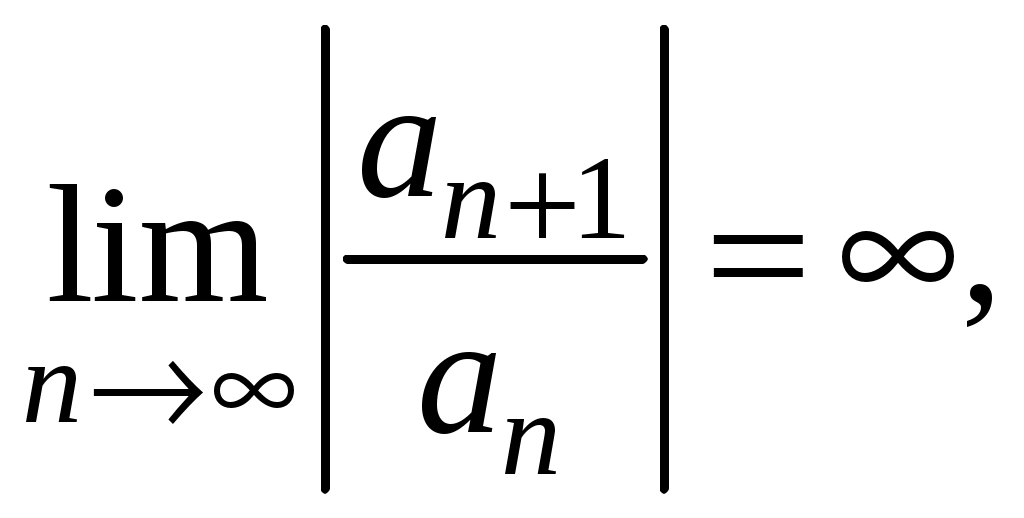 то то 2. Интервал сходимости степенного ряда (4) находят из неравенства 3. Если степенной ряд содержит не все степени х, т. е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (5) и (6)), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда. Пример 3. Найти область сходимости ряда 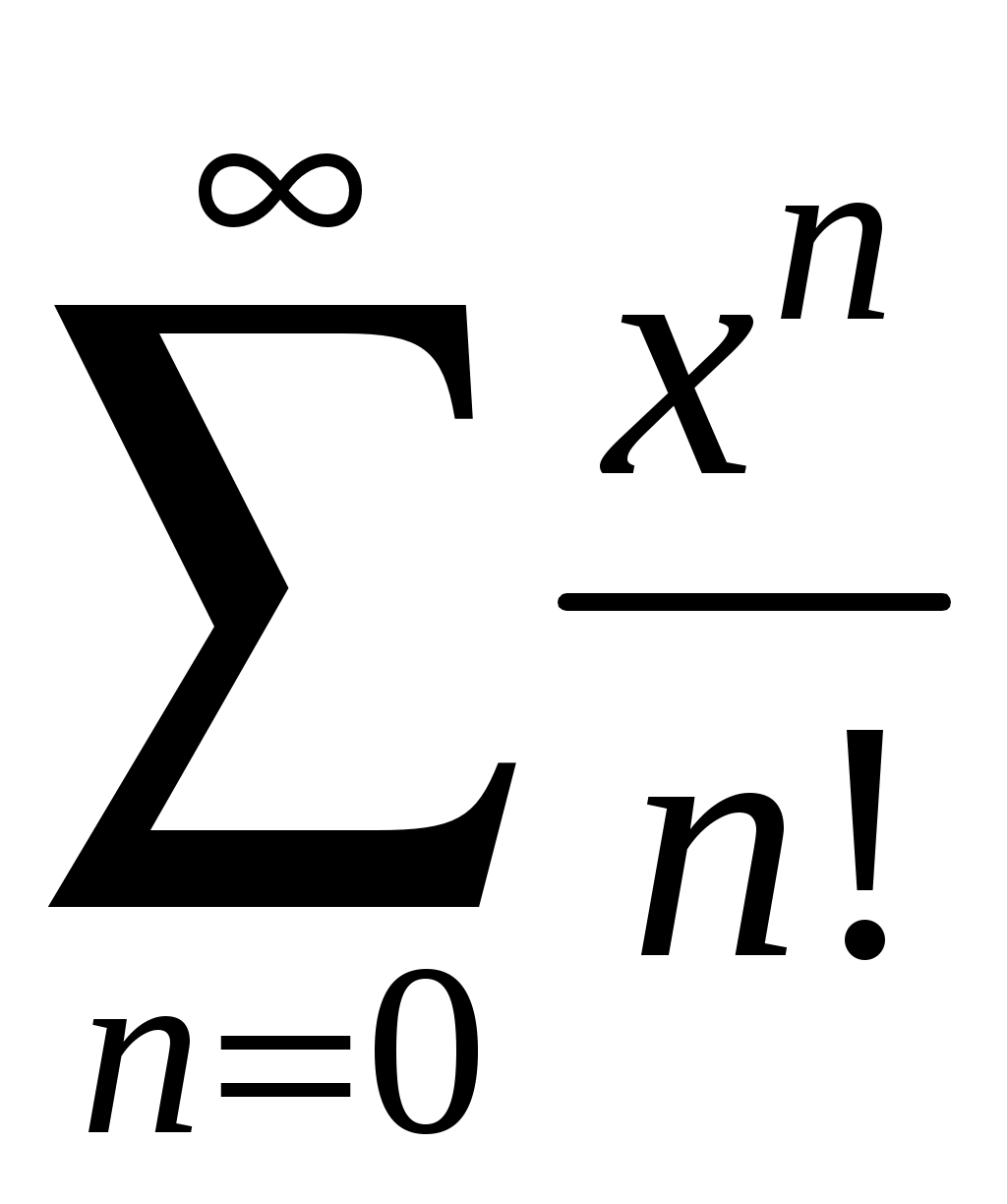 . .Решение. Воспользуемся формулой (5): 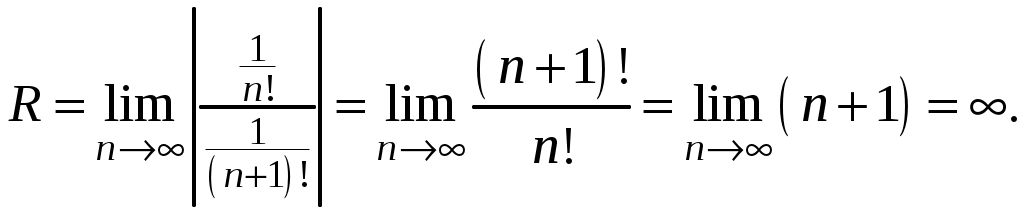 Следовательно, данный ряд абсолютно сходится на всей числовой оси. Пример 4. Найти область сходимости ряда 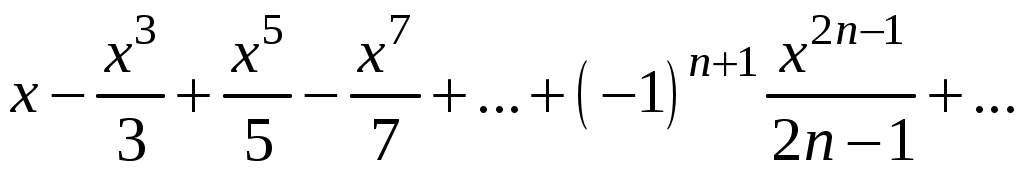 . .Решение. Заданный ряд неполный. Воспользуемся признаком Даламбера. Для данного ряда имеем: 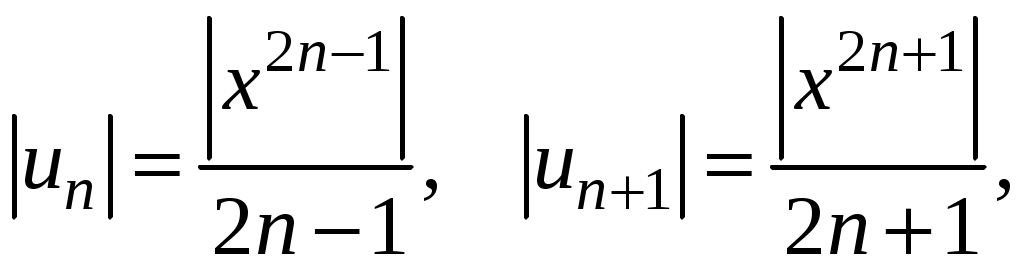 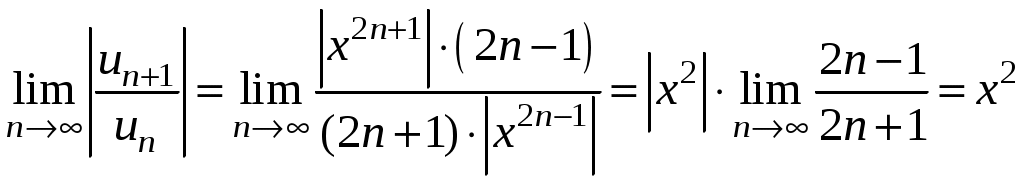 . .Ряд абсолютно сходится, если При При Пример 5. Найти область сходимости ряда 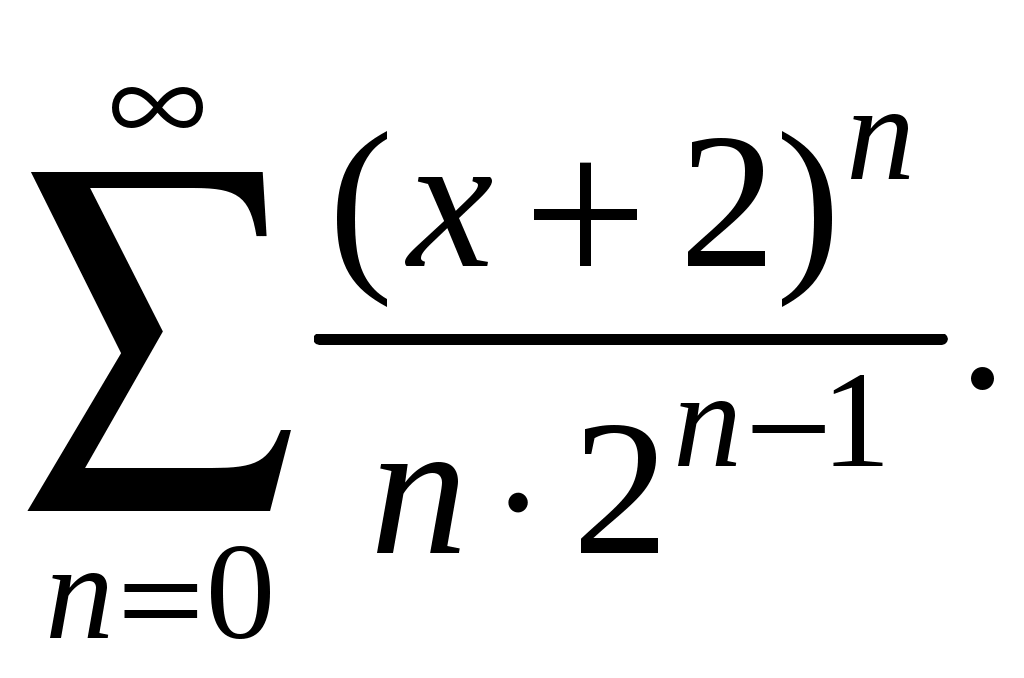 Решение. Находим радиус сходимости ряда по формуле (5): 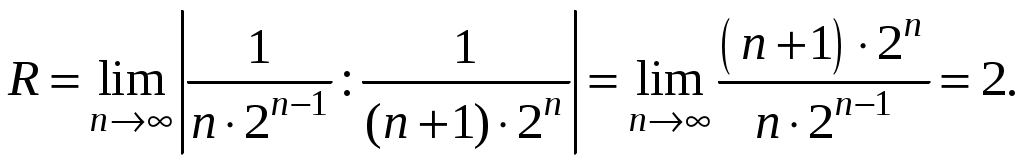 Следовательно, ряд сходится при При 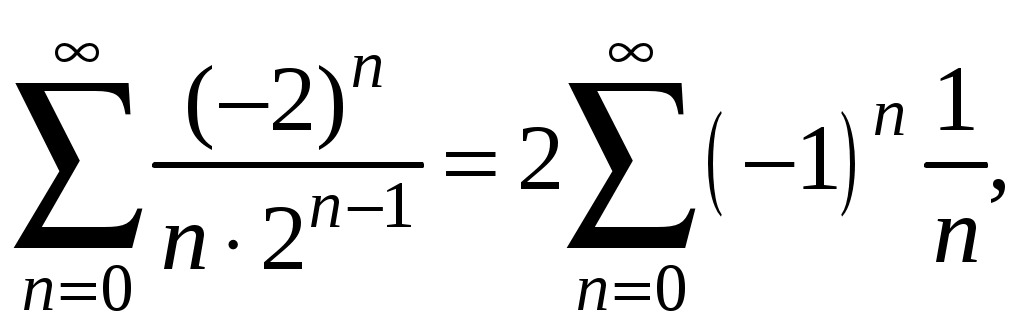 который сходится по признаку Лейбница. При 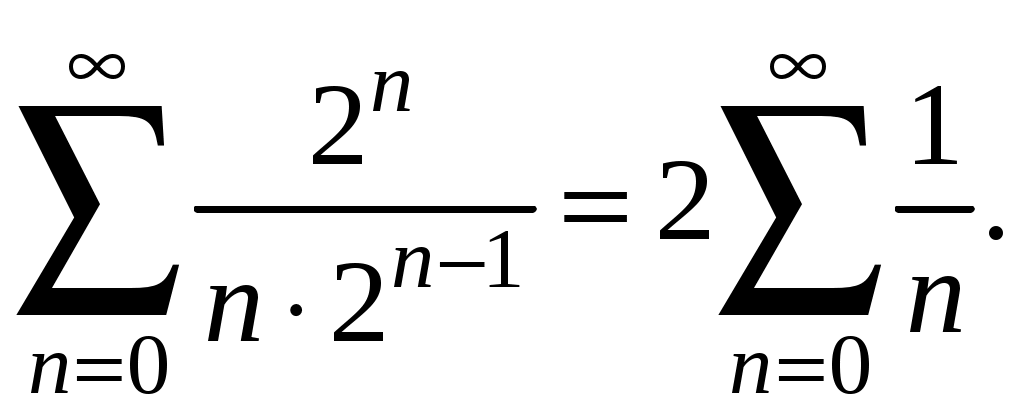 Следовательно, областью сходимости исходного ряд является полуотрезок |
