Ряды. Ряды. Основные понятия
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
|
Свойства степенных рядов Сформулируем без доказательства основные свойства степенных рядов. 1. Сумма 2. Степенные ряды 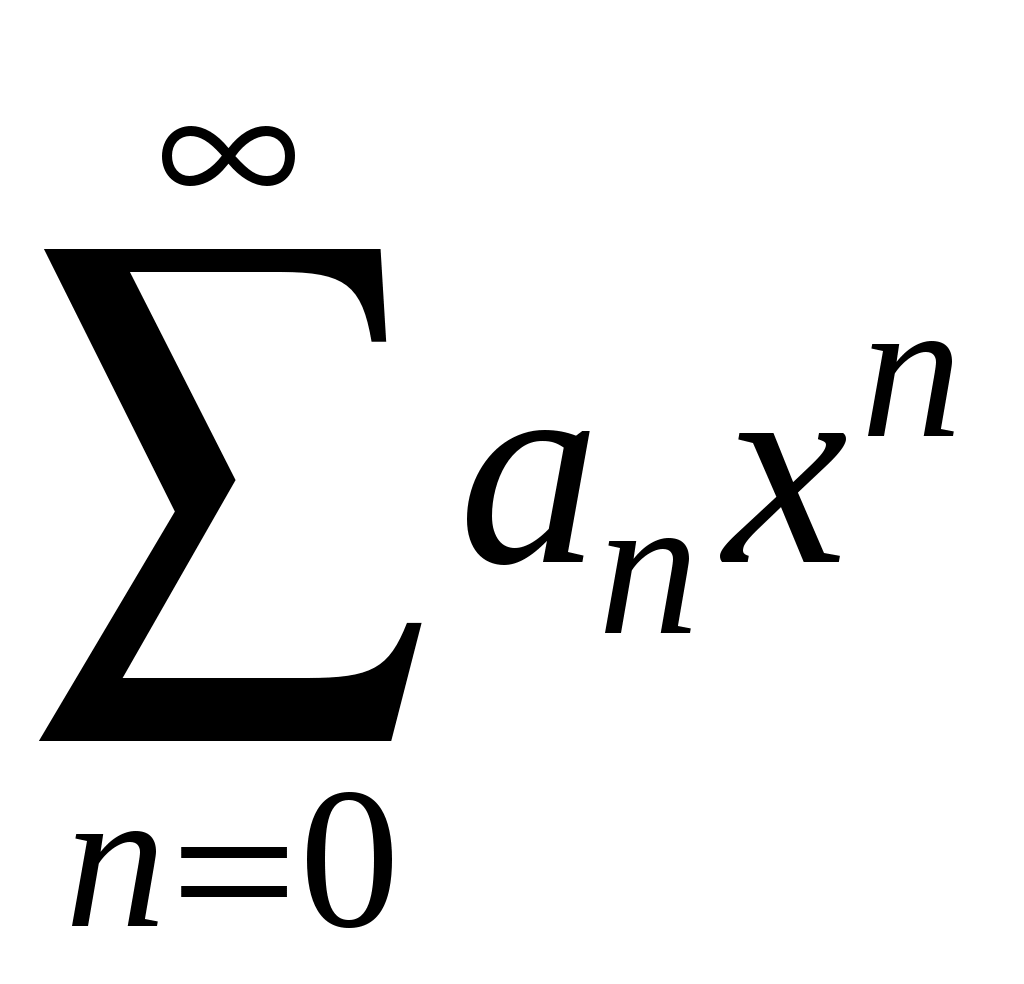 и и 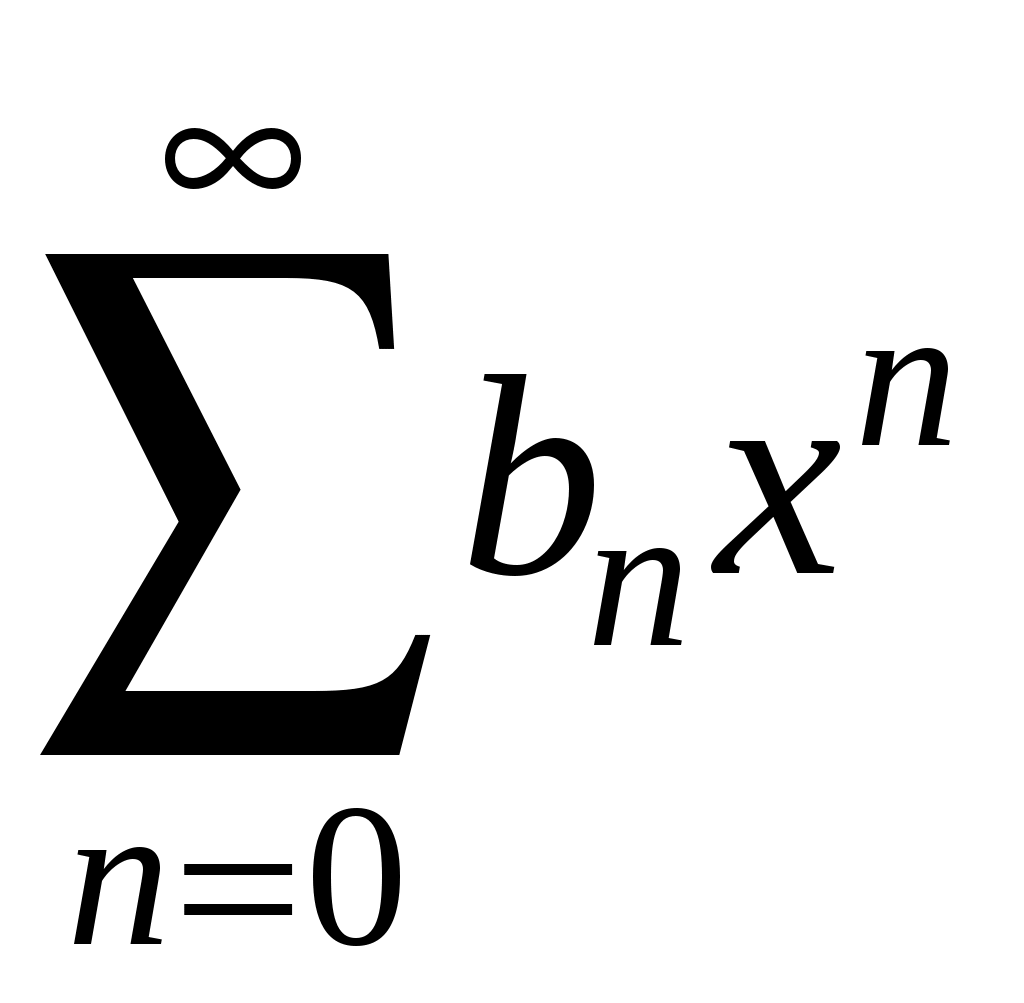 , имеющие радиусы сходимости соответственно , имеющие радиусы сходимости соответственно 3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда при 4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда (7) при 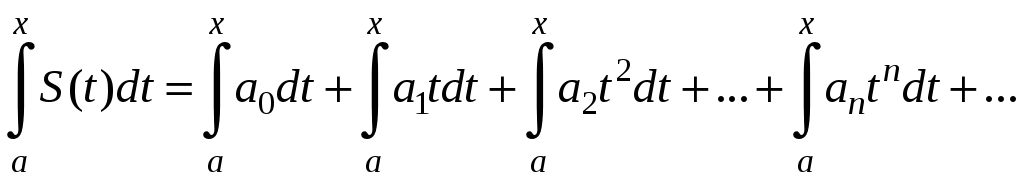 (9) (9)Ряды (7) и (8) имеют тот же радиус сходимости, что и исходный степенной ряд. Перечисленные свойства 1-4 остаются справедливыми и для степенных рядов вида (4). Свойства степенных рядов широко используются в теоретических исследованиях и в приближенных вычислениях. Разложение функций в степенные ряды 1.1. Ряды Тейлора и Маклорена Для приложений важно уметь данную функцию Как известно, для любой функции 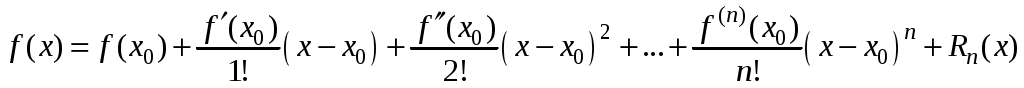 , (1.1) , (1.1) где 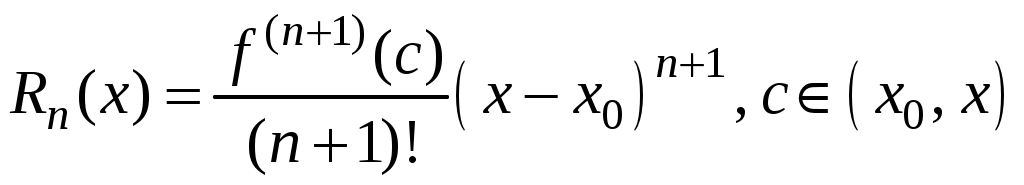 , – остаточный член в форме Лагранжа. Число с можно записать в виде , – остаточный член в форме Лагранжа. Число с можно записать в виде где 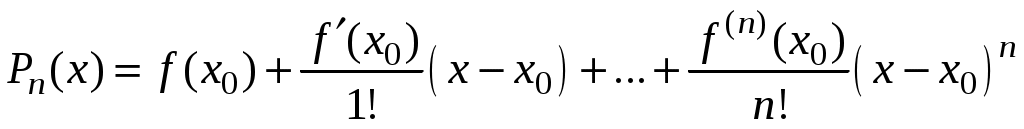 – многочлен Тейлора. – многочлен Тейлора.Если функция 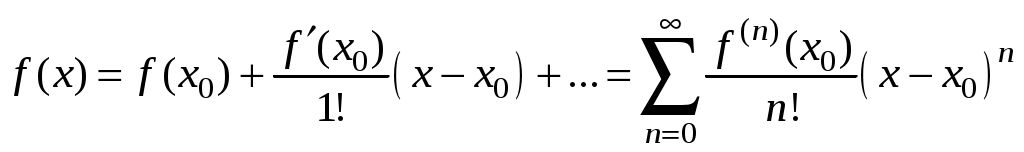 (1.2) (1.2)Если в ряде Тейлора положить 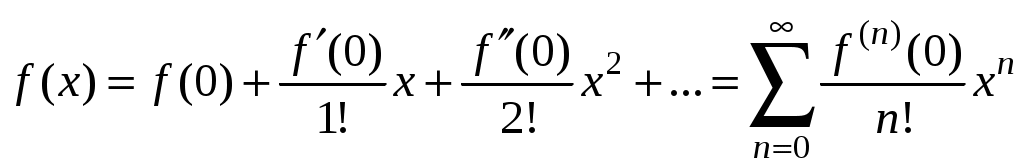 (1.3) (1.3)Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки 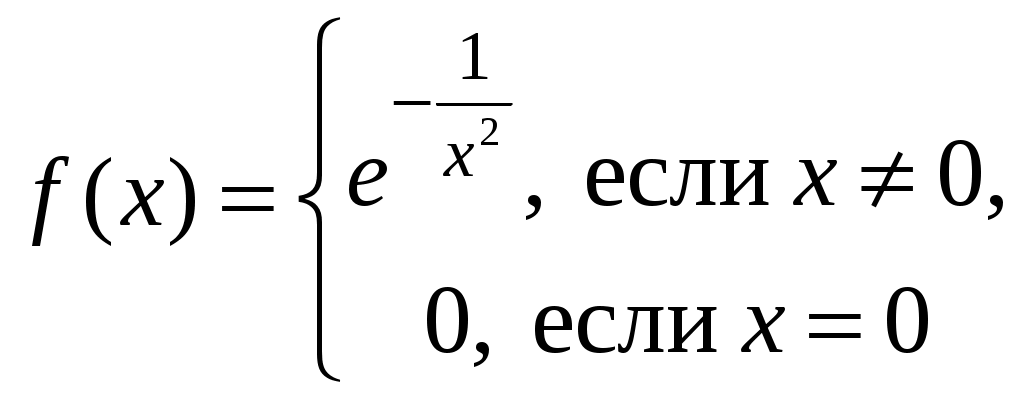 имеет в точке Ряд Маклорена имеет вид Он сходится, но его сумма Пусть для функции Теорема 1. Для того, чтобы ряд Тейлора (1.2) функции Пусть ряд Тейлора (1.2) сходится к функции 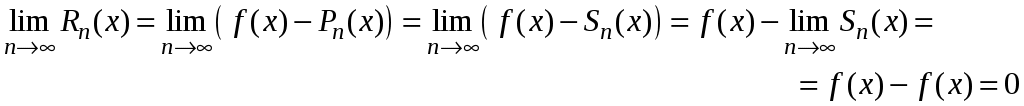 Обратно, Замечание. Если ряд Тейлора (1.2) сходится к порождающей функции Таким образом, задача разложения функции На практике часто пользуются следующей теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора. Теорема 2. Если модули всех производных функций Согласно теореме 1, достаточно показать, что 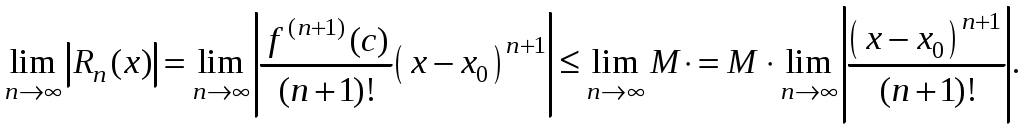 Осталось показать, что 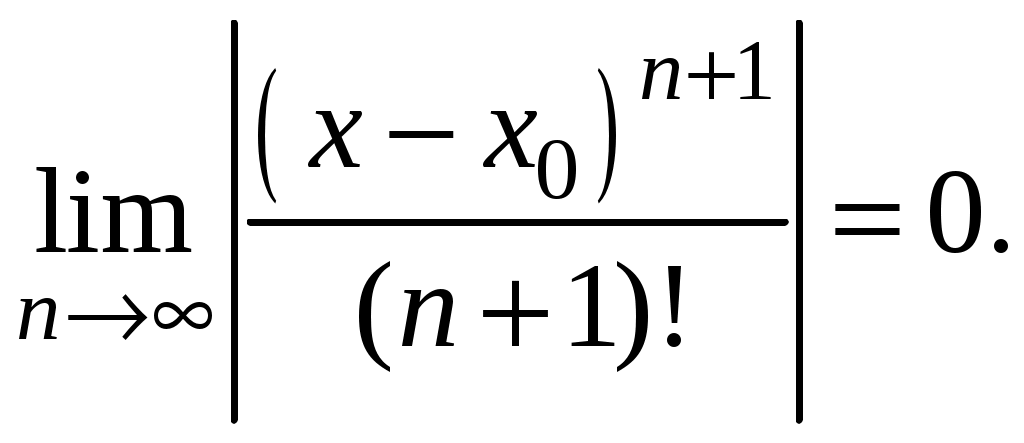 Для этого рассмотрим ряд Для этого рассмотрим ряд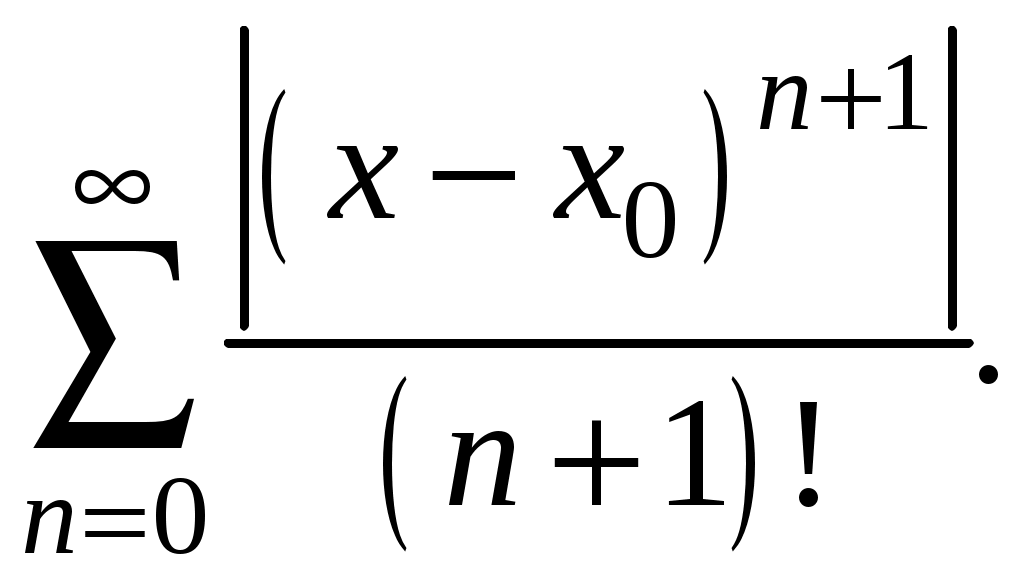 Так как 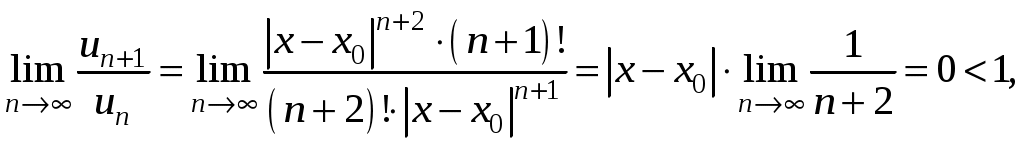 то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда в силу необходимого признака сходимости, 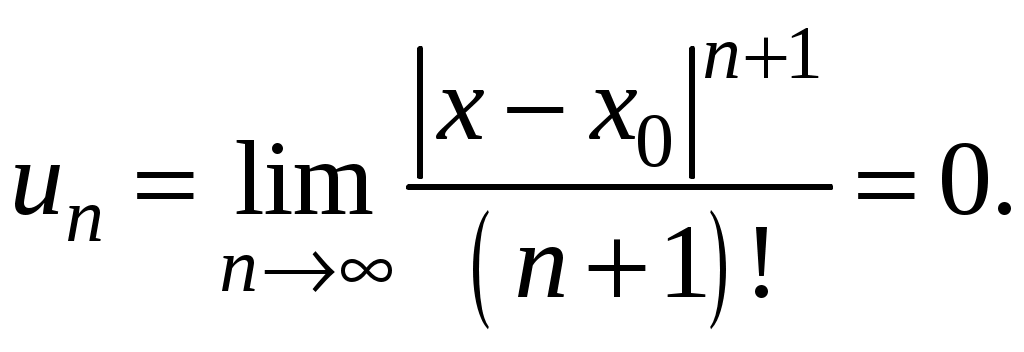 Следовательно, 1.2. Разложение некоторых элементарных функций в ряд Тейлора (Маклорена) Для разложения функции а) найти производные б) вычислить значения производных в точке в) написать ряд (1.3) для заданной функции и найти его интервал сходимости; г) найти интервал Замечание. В интервале сходимости степенного ряда остаточный член стремится к нулю при Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций (эти разложения следует запомнить): 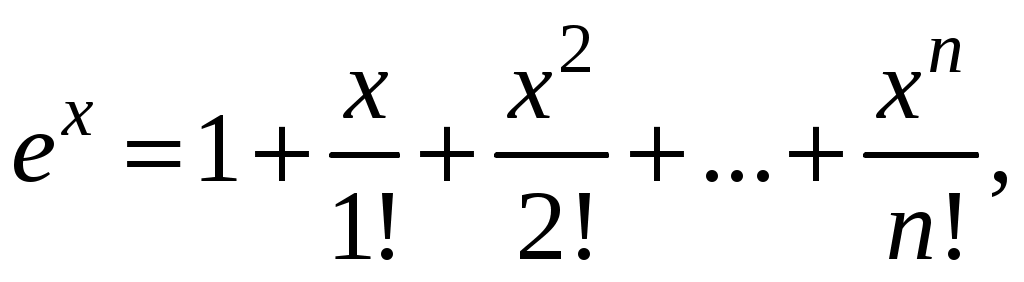 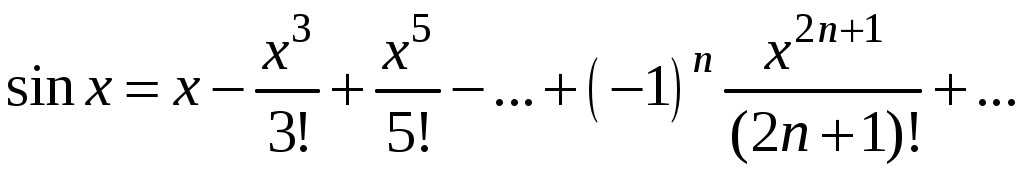 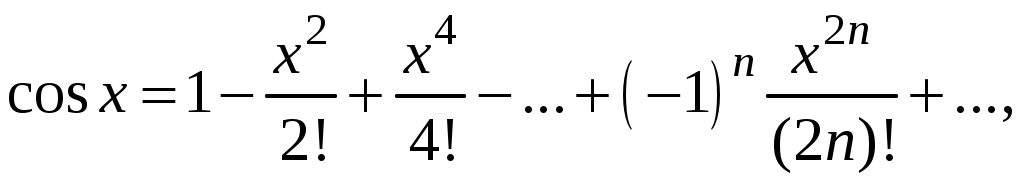 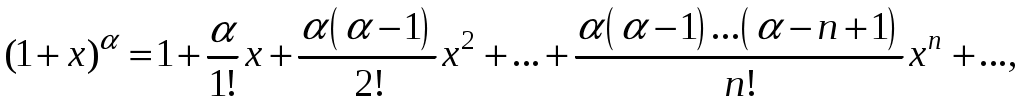 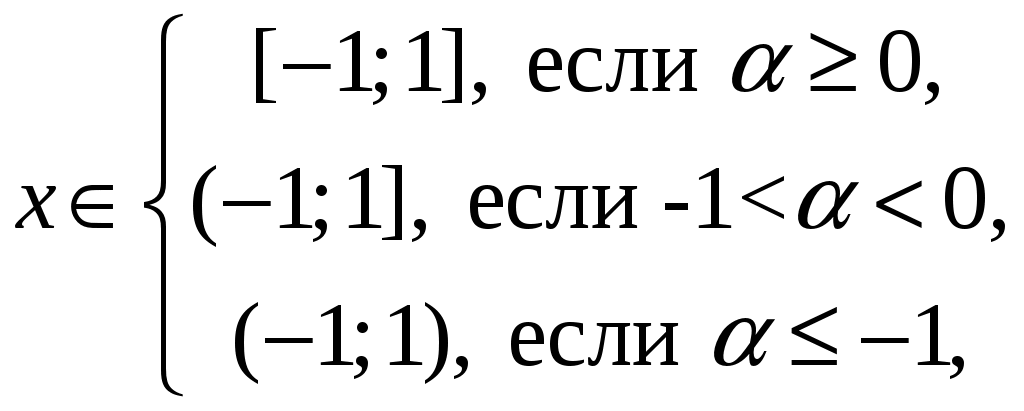 (1.7) (1.7)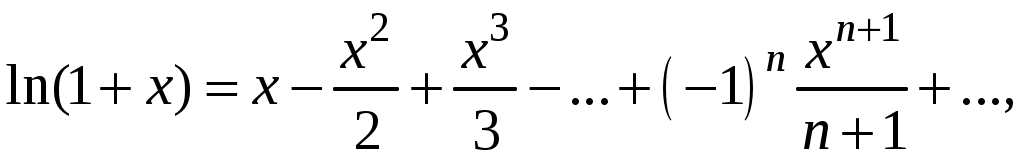 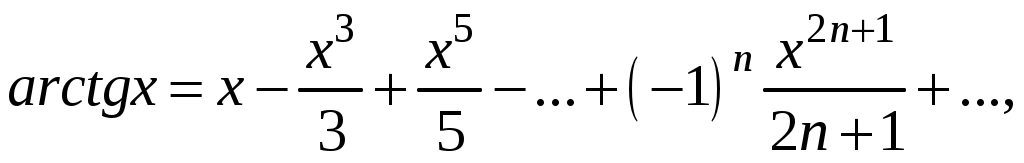 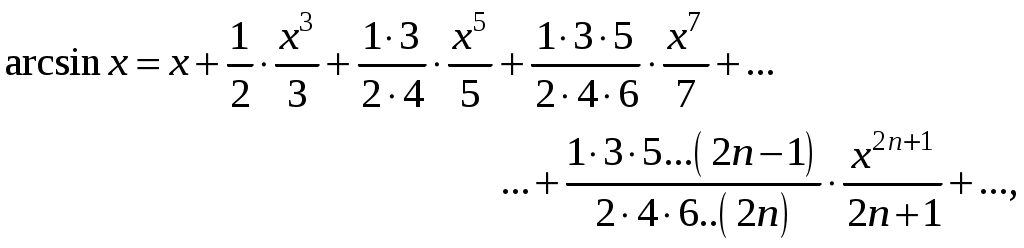 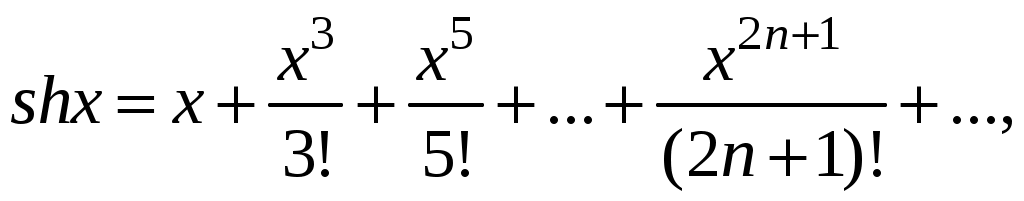 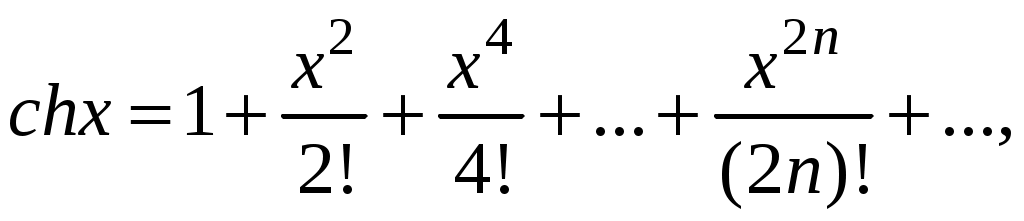 Докажем формулу (1.4). Пусть Имеем: 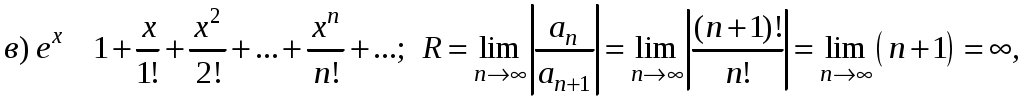 т. е. ряд сходится в интервале г) для всех 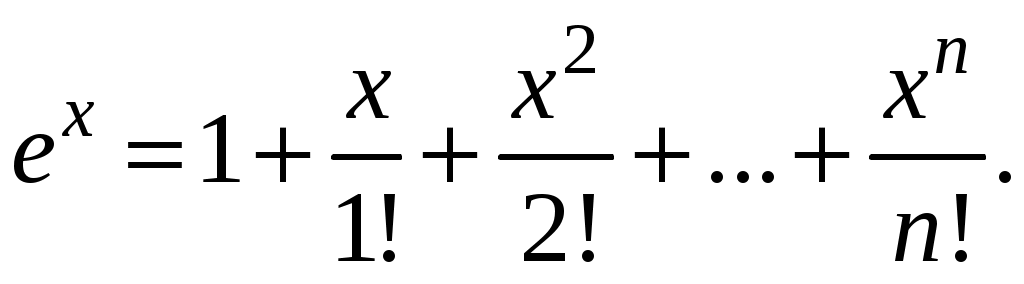 Докажем формулу (1.5). Пусть Имеем: 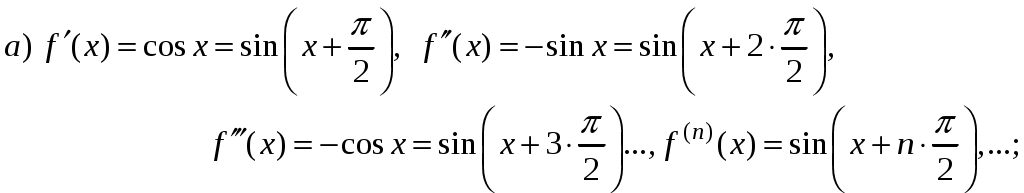 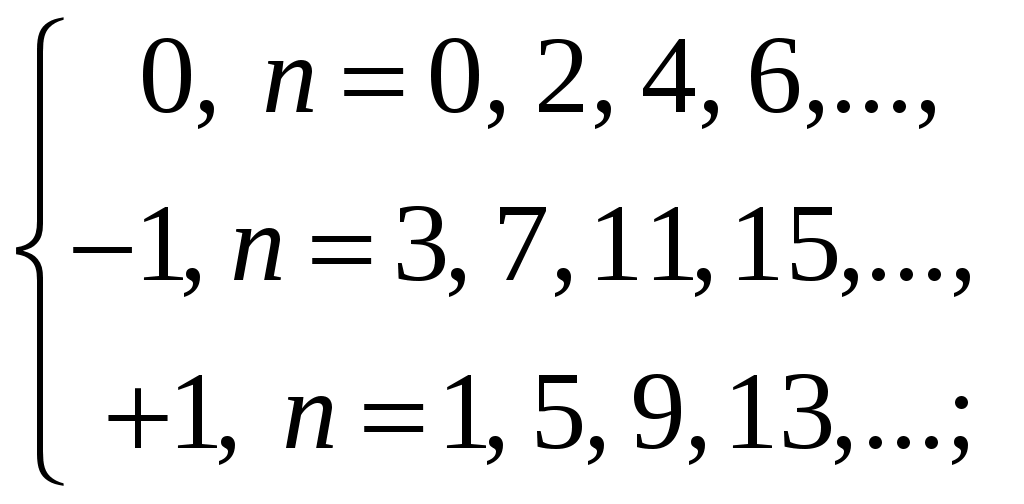 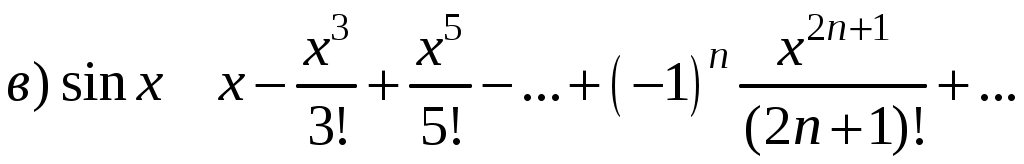 Легко проверить, что полученный ряд сходится на всей числовой оси, т. е. при всех Легко проверить, что полученный ряд сходится на всей числовой оси, т. е. при всех 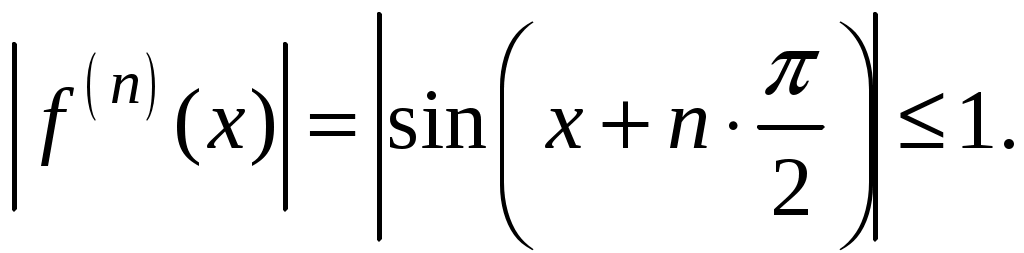 Следовательно, по теореме 2 имеет место разложение (1.5). Пример 1. Разложить в ряд Маклорена функцию Решение. Так как 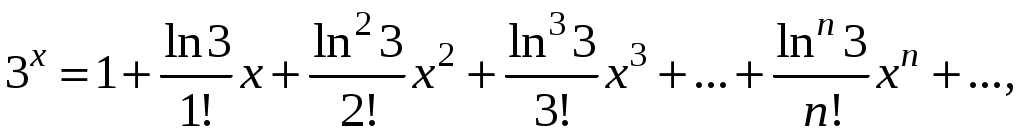 Пример 2. Выписать ряд Маклорена функции Решение. Так как 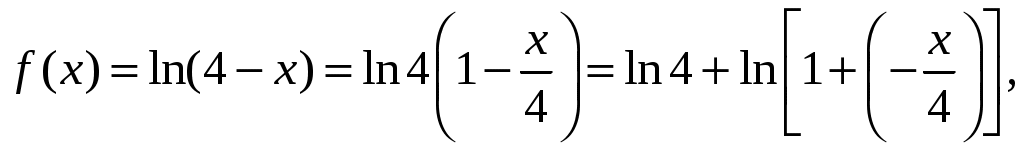 то, воспользовавшись формулой (1.9), в которой заменим х на 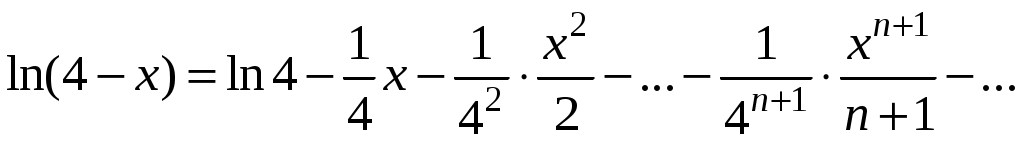 , ,если |
