Ряды. Ряды. Основные понятия
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
|
Достаточные признаки сходимости знакопостоянных рядов. Признаки сравнения рядов Необходимы признак сходимости не дает, вообще говоря, возможности судить о том, сходится ли данный ряд или нет. Сходимость и расходимость ряда в многих случаях можно установить с помощью так называемых достаточных признаков. Рассмотрим некоторые из них для знакоположительных рядов, т. е. рядов с неотрицательными членами (знакоотрицательный ряд переходит в знакоположительный путем умножения его на (–1), что, как известно, не влияет на сходимость ряда). Сходимость или расходимость знакоположительного ряда часто устанавливается путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы. Теорема 1. Пусть даны два знакоположительных ряда и Если для всех n выполняется неравенство то из сходимости ряда (2) следует сходимость ряда (1), из расходимости ряда (1) следует расходимость ряда (2). Обозначим n-е частичные суммы рядов (1) и (2) соответственно через Пусть ряд (2) сходится и его сумма равна S2. Тогда Пусть теперь ряд (1) расходится. Так как члены ряда неотрицательны, в этом случае имеем Замечание. Теорема 1 справедлива и в том случае, когда неравенство (3) выполняется не для всех членов ряда (1) и (2), а начиная с некоторого номера N. Это вытекает из свойства 3 числовых рядов. Теорема 2 (предельный признак сравнения). Пусть даны два знакоположительных ряда (1) и (2). Если существует конечный, отличный от 0, предел 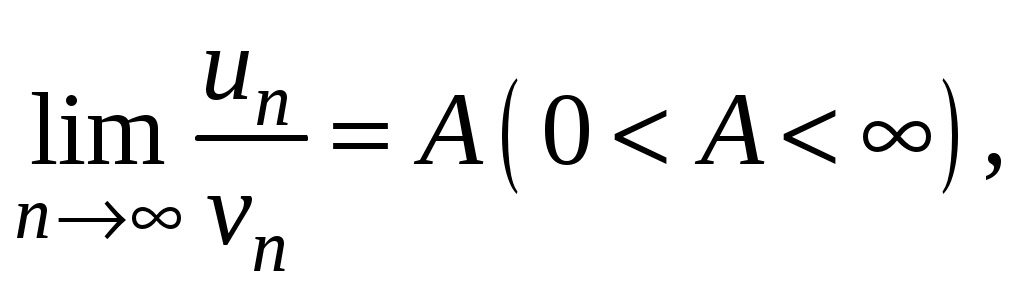 то ряды (1) и (2) сходятся или расходятся одновременно. то ряды (1) и (2) сходятся или расходятся одновременно.По определению предела последовательности для всех n, кроме, возможно, конечного числа их, для любого 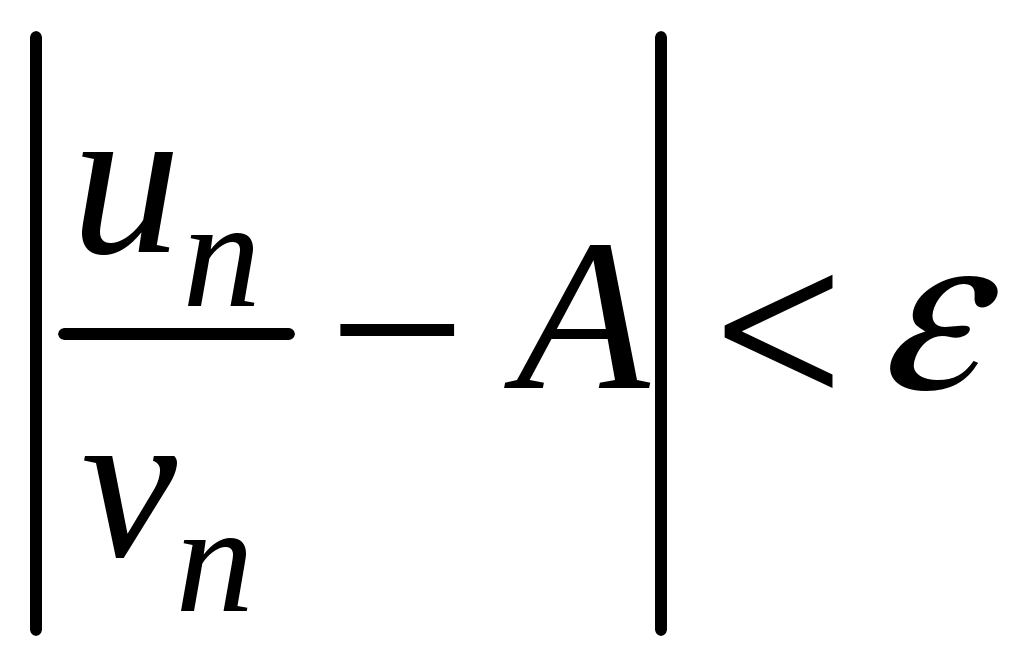 , или , илиЕсли ряд (1) сходится, то из левого равенства (5) и теоремы 1 вытекает, что ряд 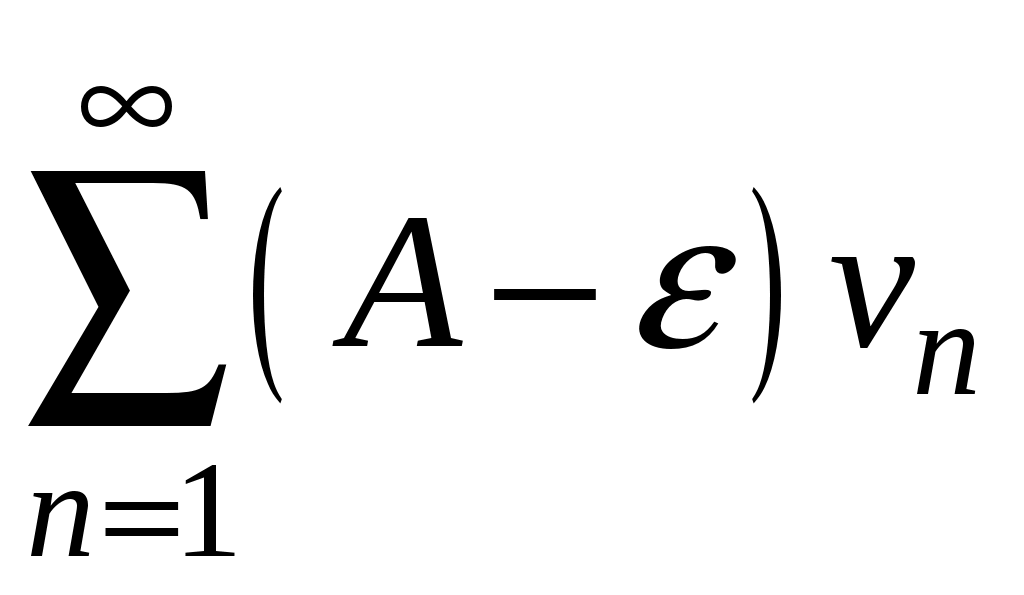 также сходится. Но тогда, согласно свойству 1 числовых рядов, ряд (2) расходится. также сходится. Но тогда, согласно свойству 1 числовых рядов, ряд (2) расходится.Если ряд (1) расходится, то из правого неравенства (5), теоремы 1, свойства 1 вытекает, что и ряд (2) расходится. Аналогично, если ряд (2) сходится (расходится), то сходящимся (расходящимся) будет и ряд (1). Пример 1. Исследовать на сходимость ряд 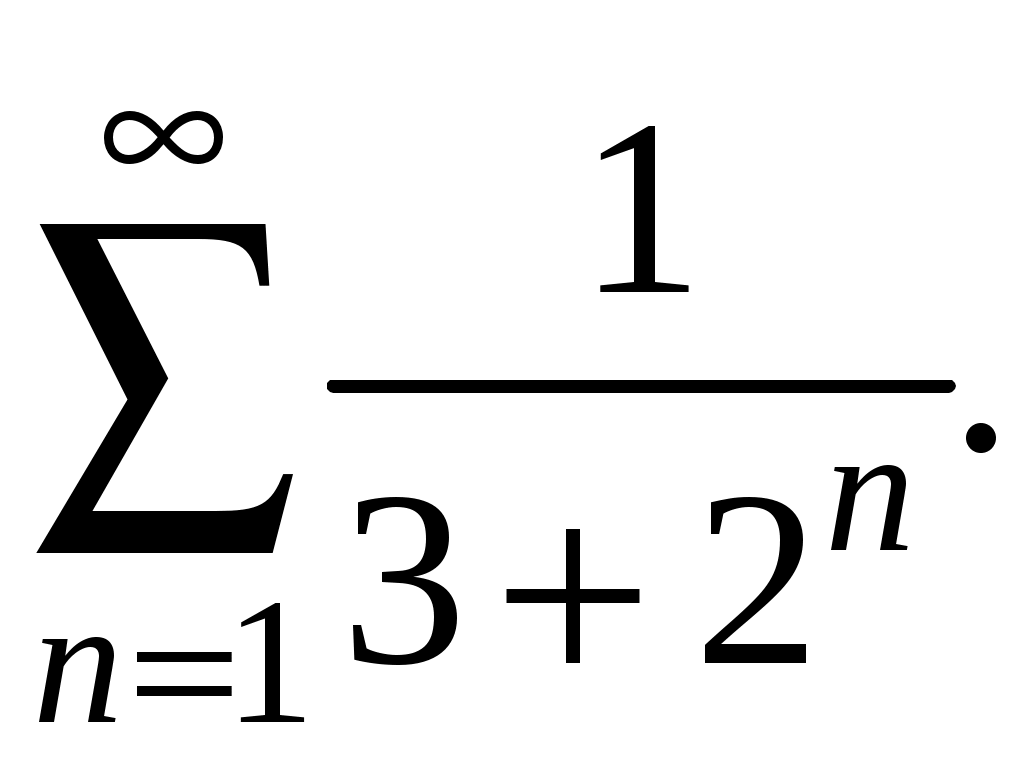 Решение: Сравним данный ряд с рядом геометрической прогрессии 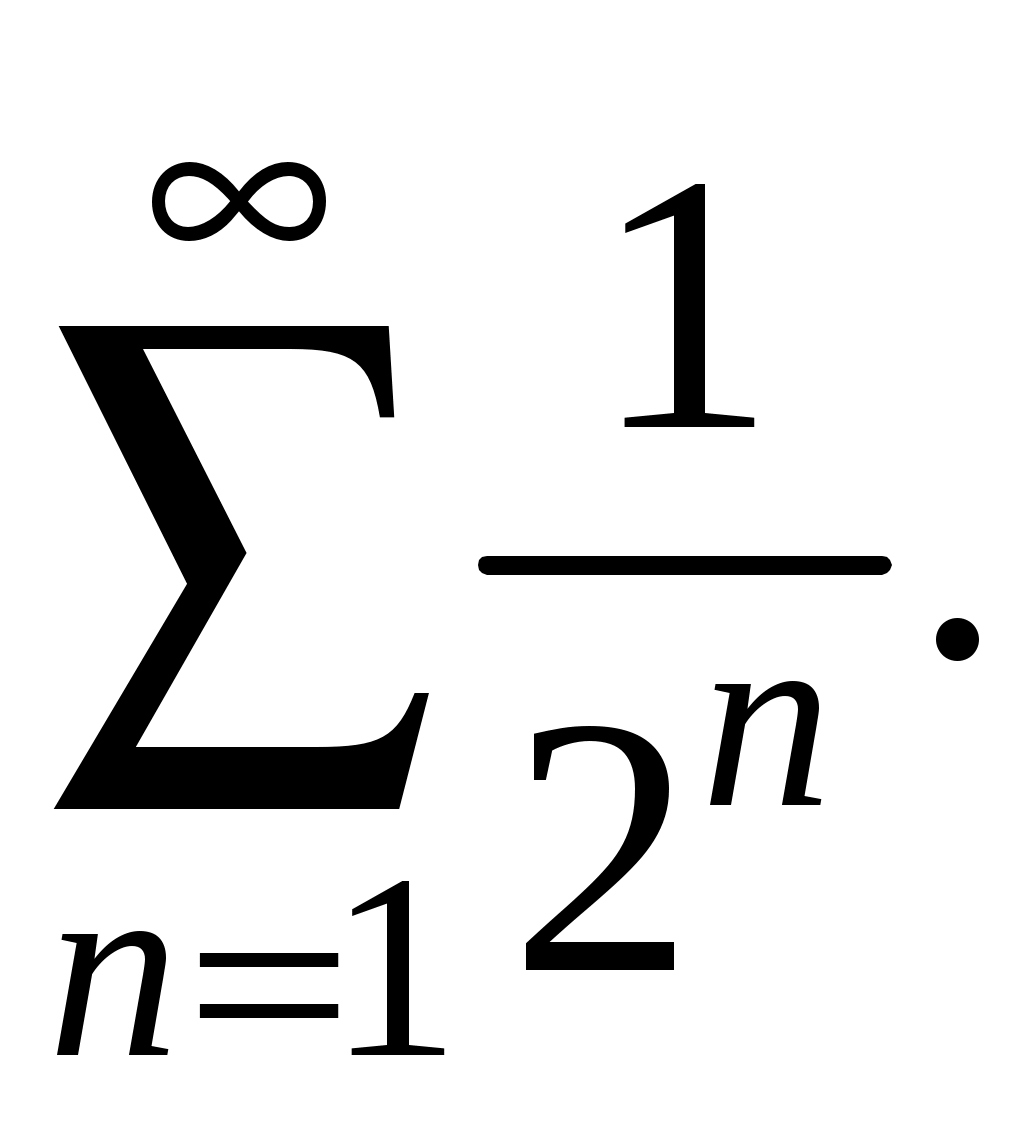 который сходится который сходится 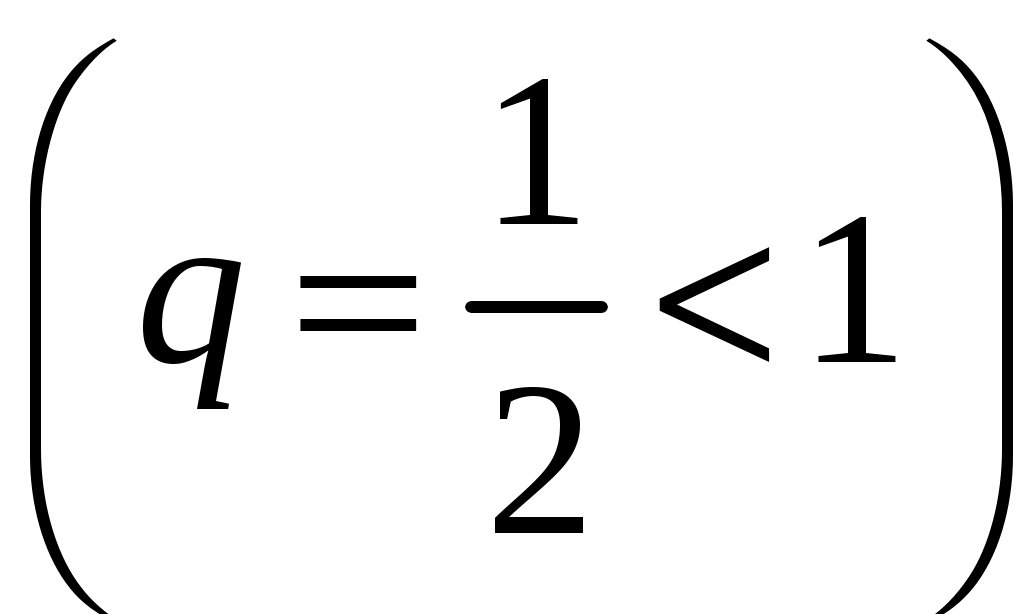 . Имеем . Имеем Пример 2. Исследовать сходимость ряда 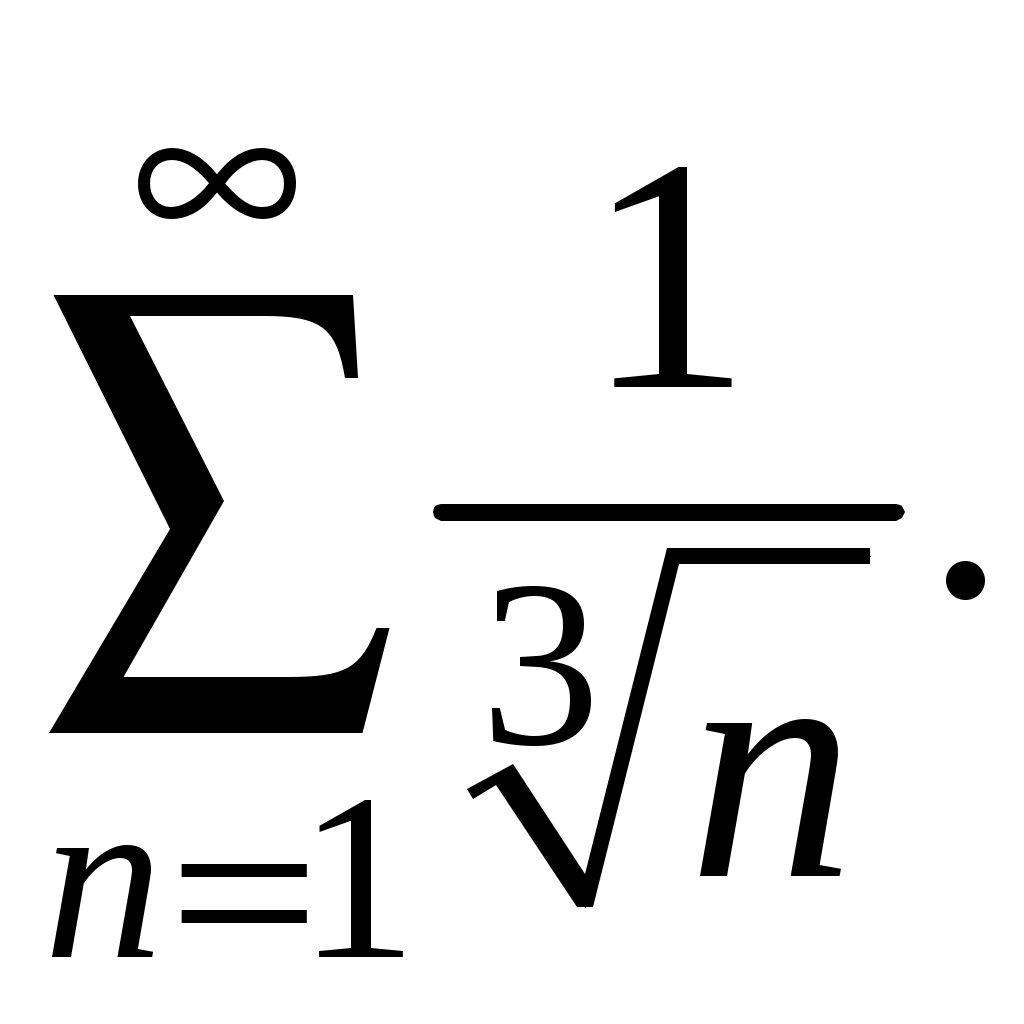 Решение: Здесь 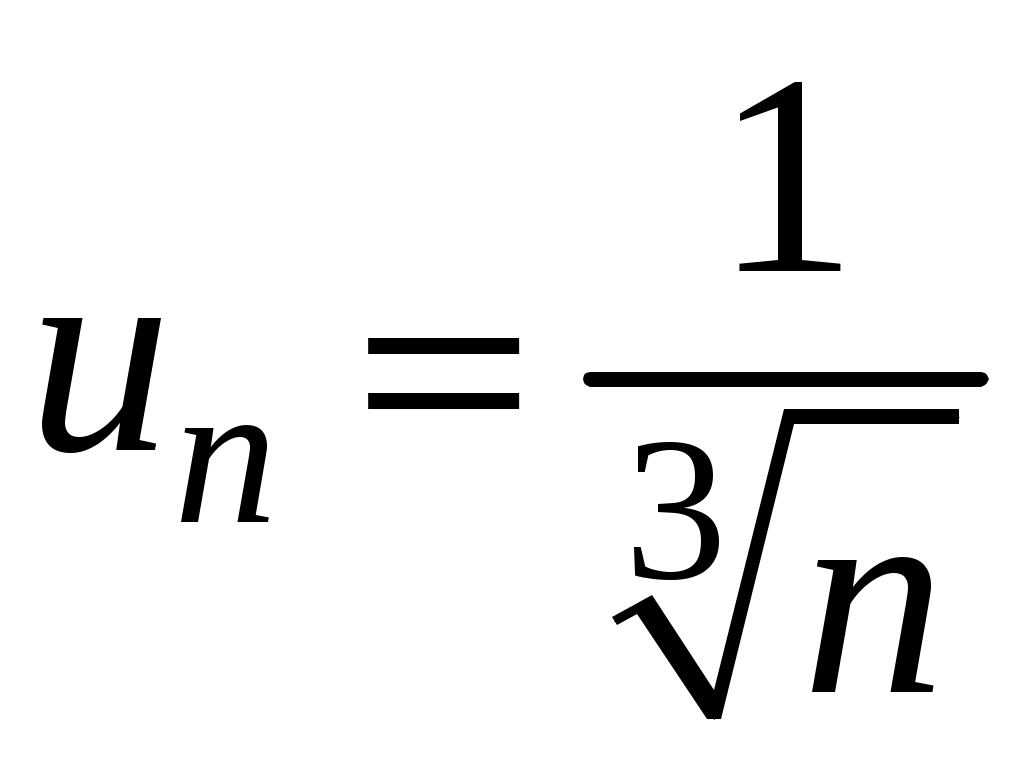 . Возьмем ряд с общим членом . Возьмем ряд с общим членом 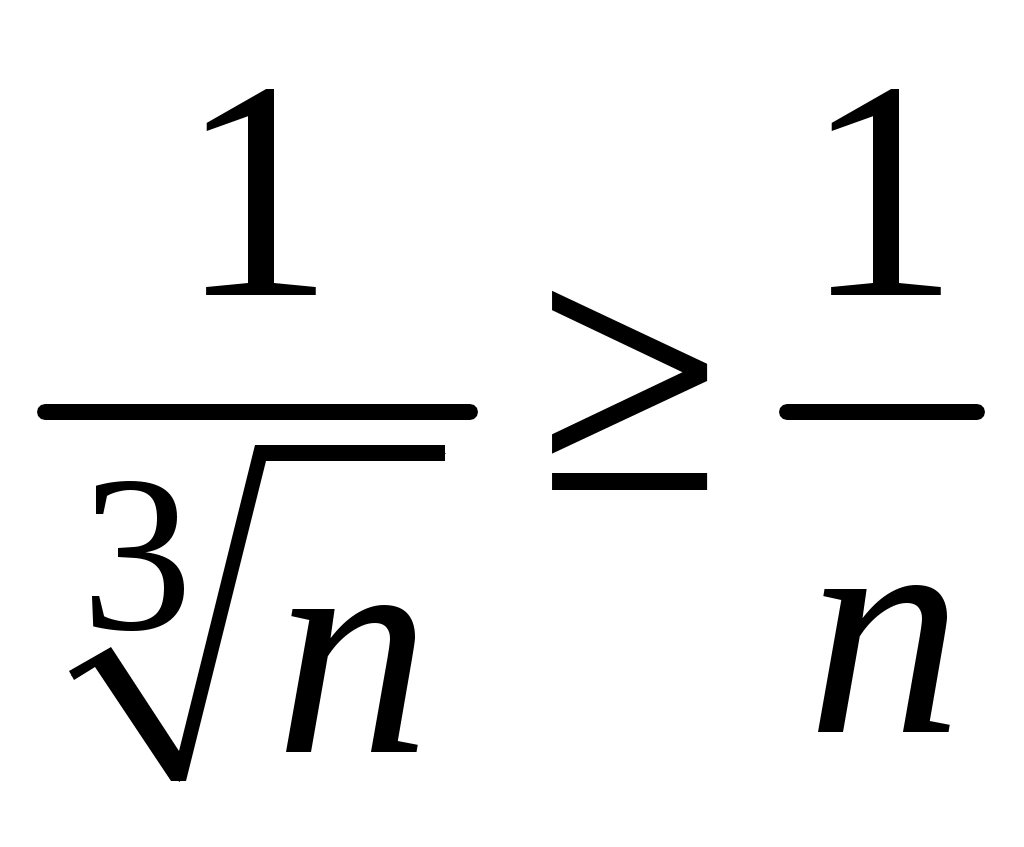 . Следовательно, данный ряд расходится. . Следовательно, данный ряд расходится.Пример 3. Исследовать сходимость ряда 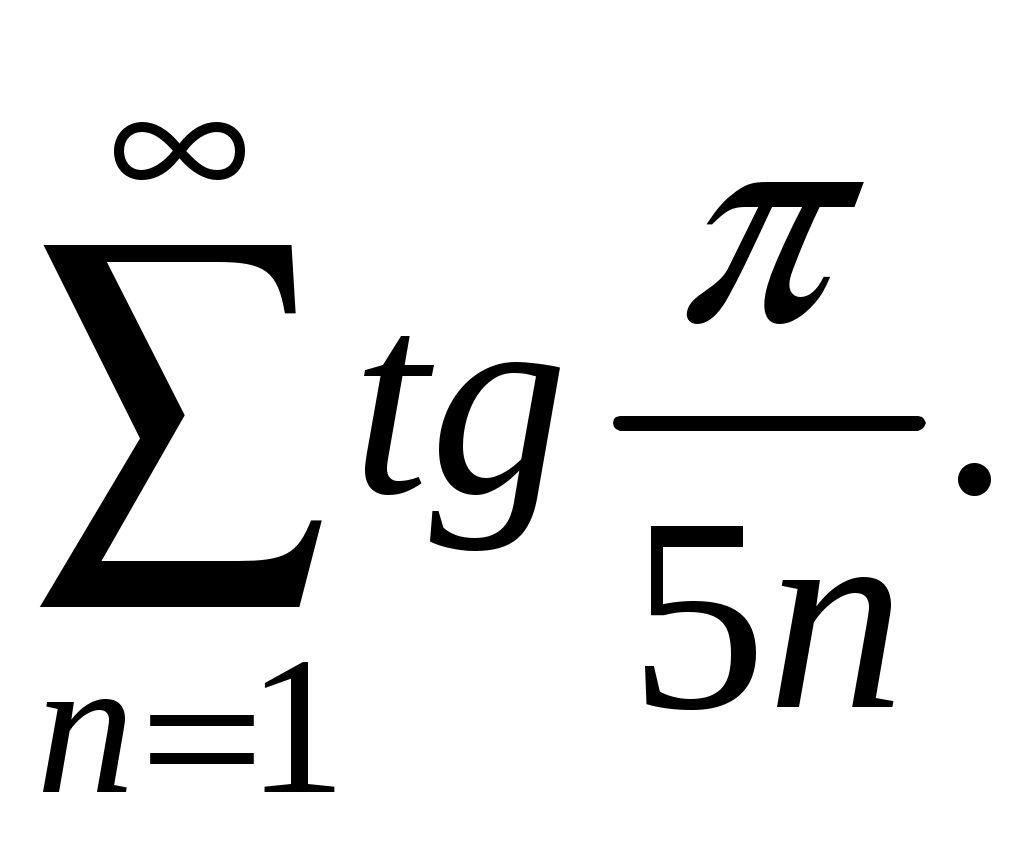 Решение: Применим предельный признак сравнения. Так как 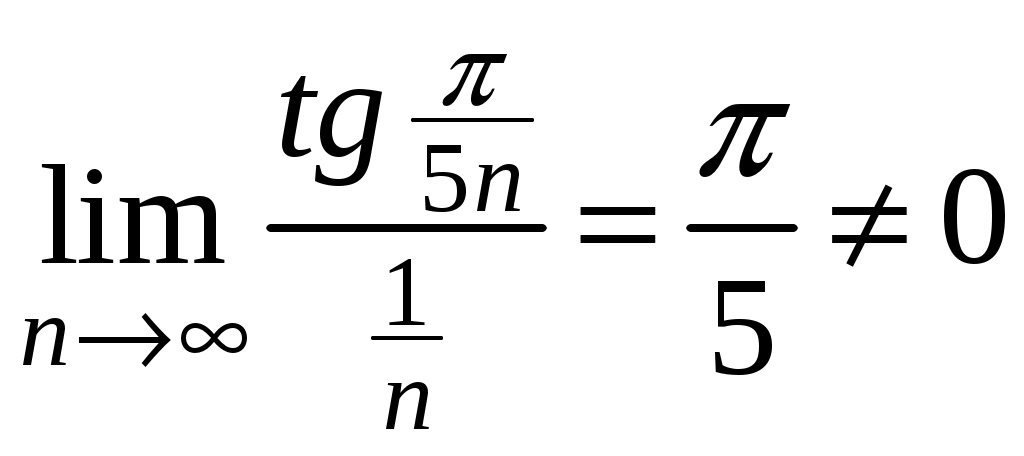 , ,То по теореме 2 исходный ряд расходится, как сравнимый с гармоническим рядом. Признак Даламбера В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717-1783, французский математик) позволяет часто решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом. Теорема 3. Пусть дан ряд с положительными членами 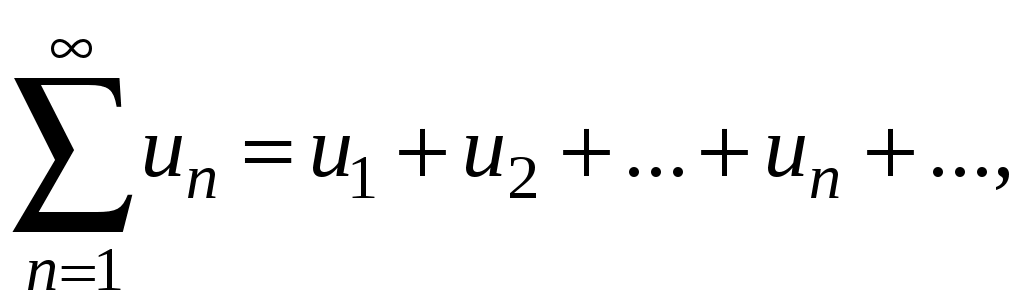 (6) (6)и существует конечный или бесконечный предел 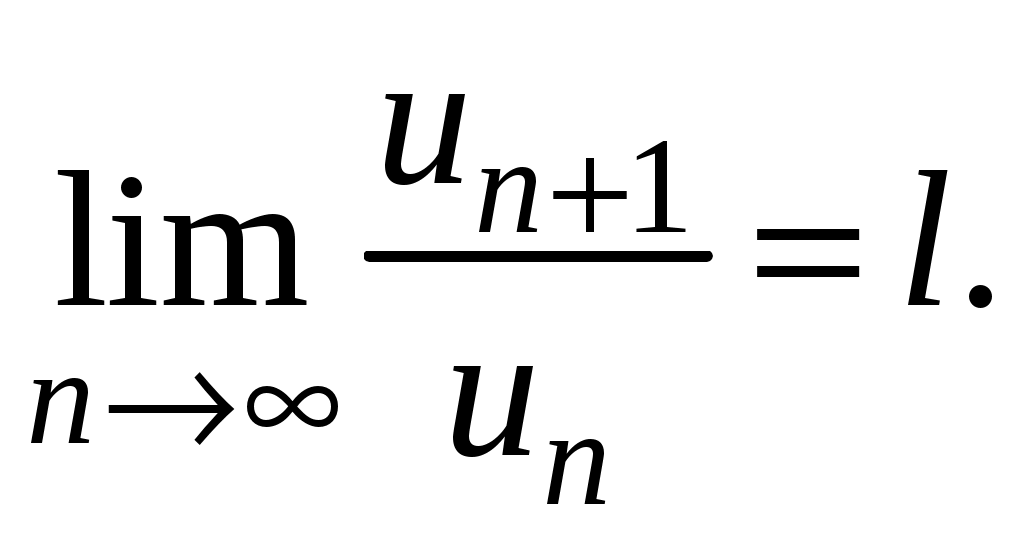 Тогда ряд сходится при Тогда ряд сходится при Так как 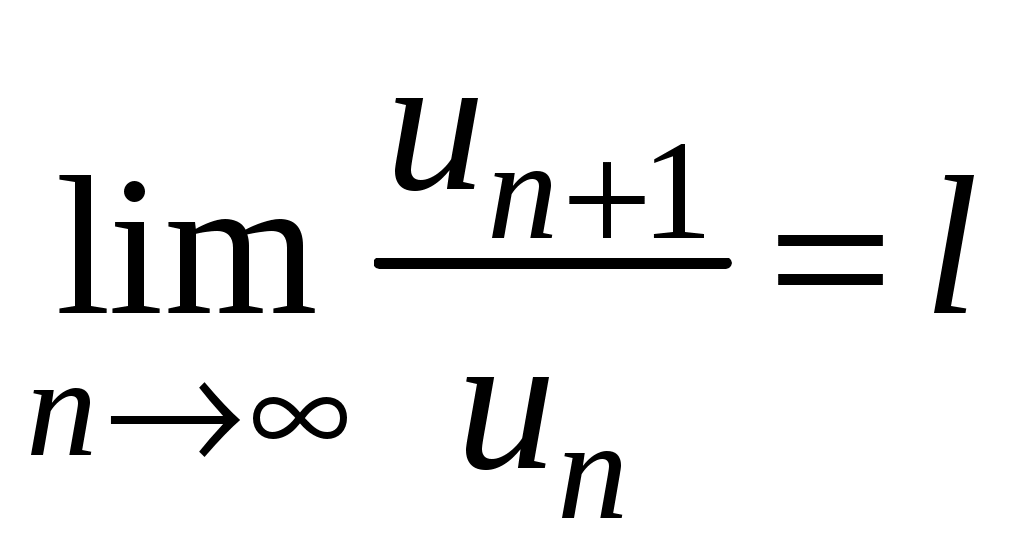 , то по определению предела для любого , то по определению предела для любого 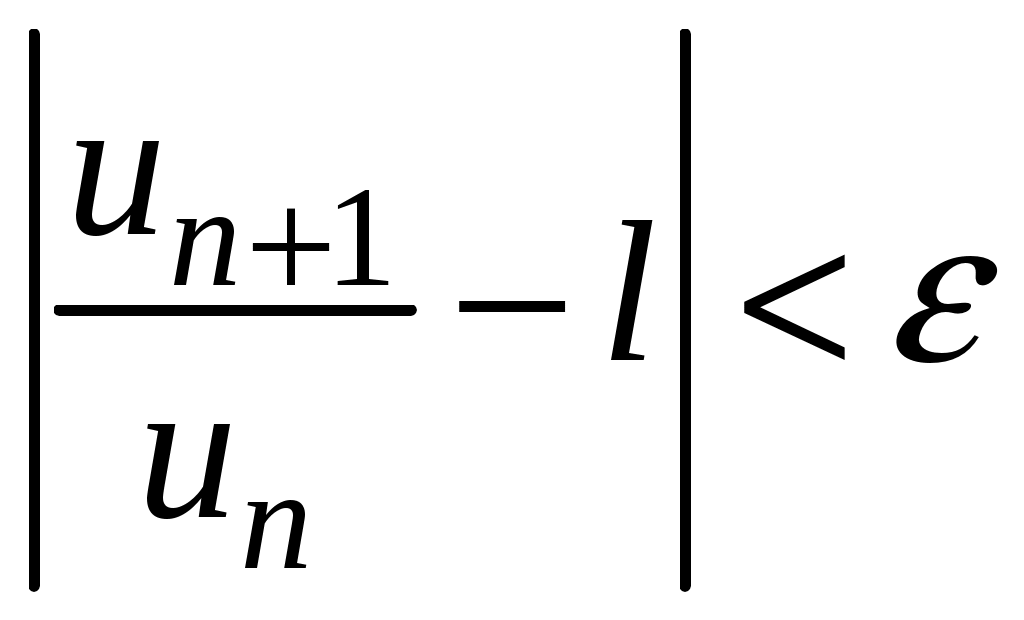 или или 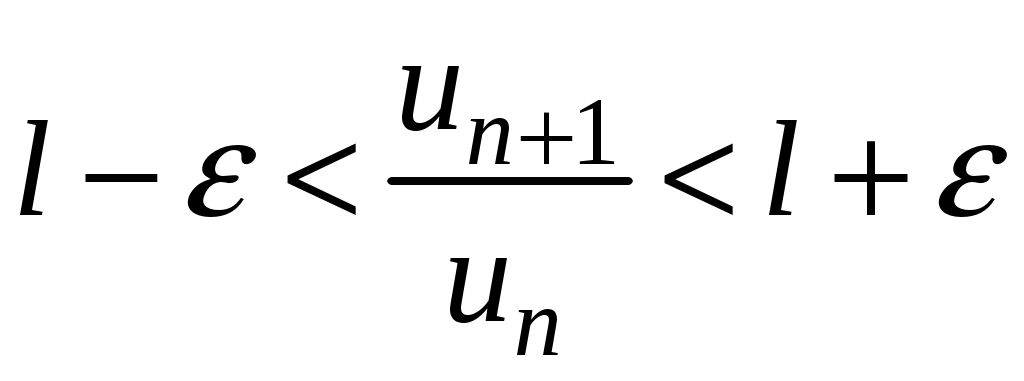 . (7) . (7)Пусть 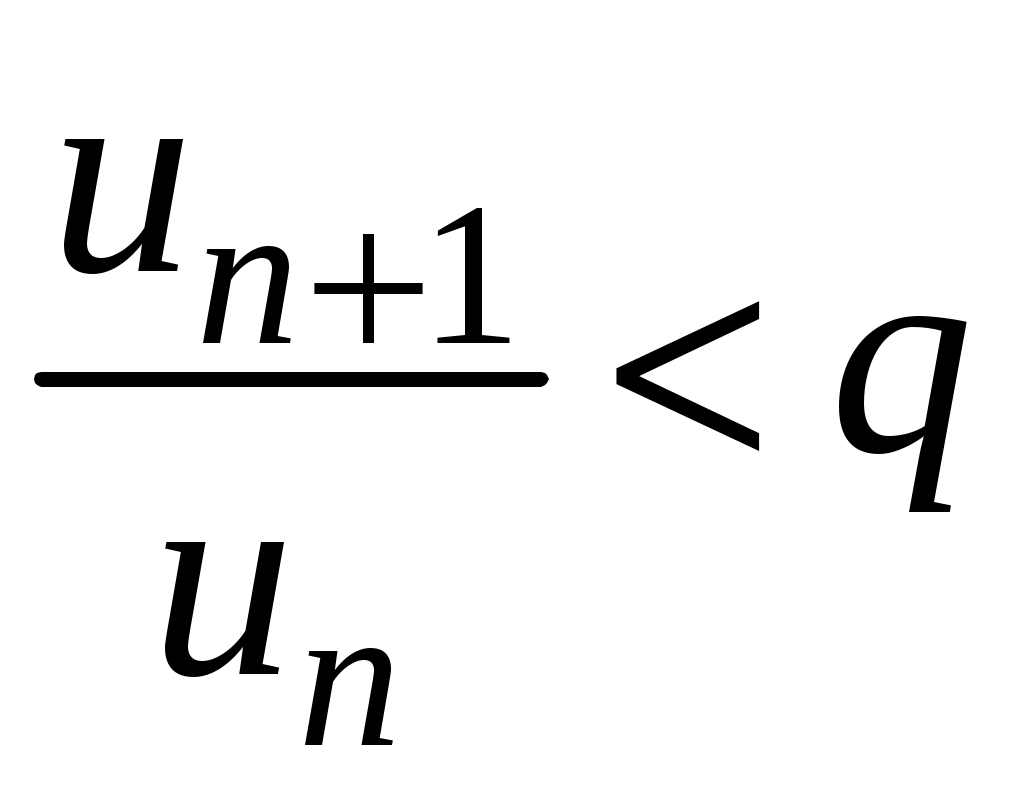 , или , или ………………… …………………. т. е. члены ряда Пусть 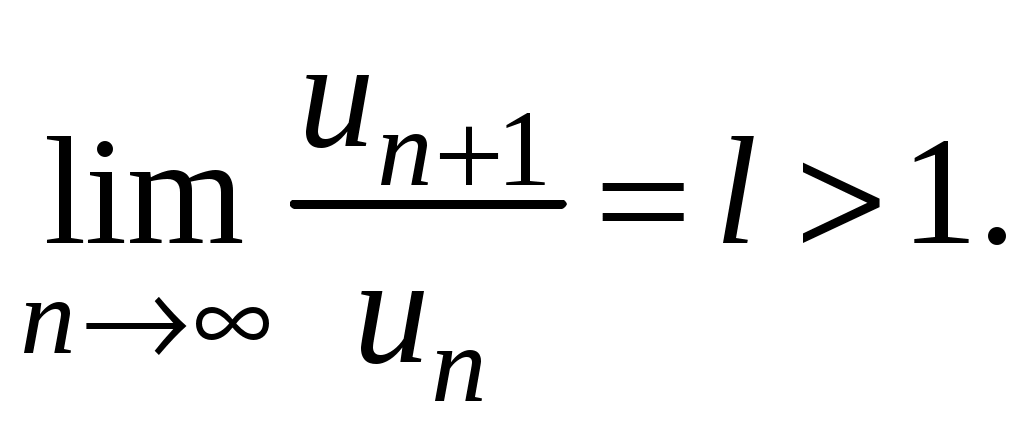 Отсюда следует, что, начиная с некоторого номера N, выполняется неравенство Отсюда следует, что, начиная с некоторого номера N, выполняется неравенство 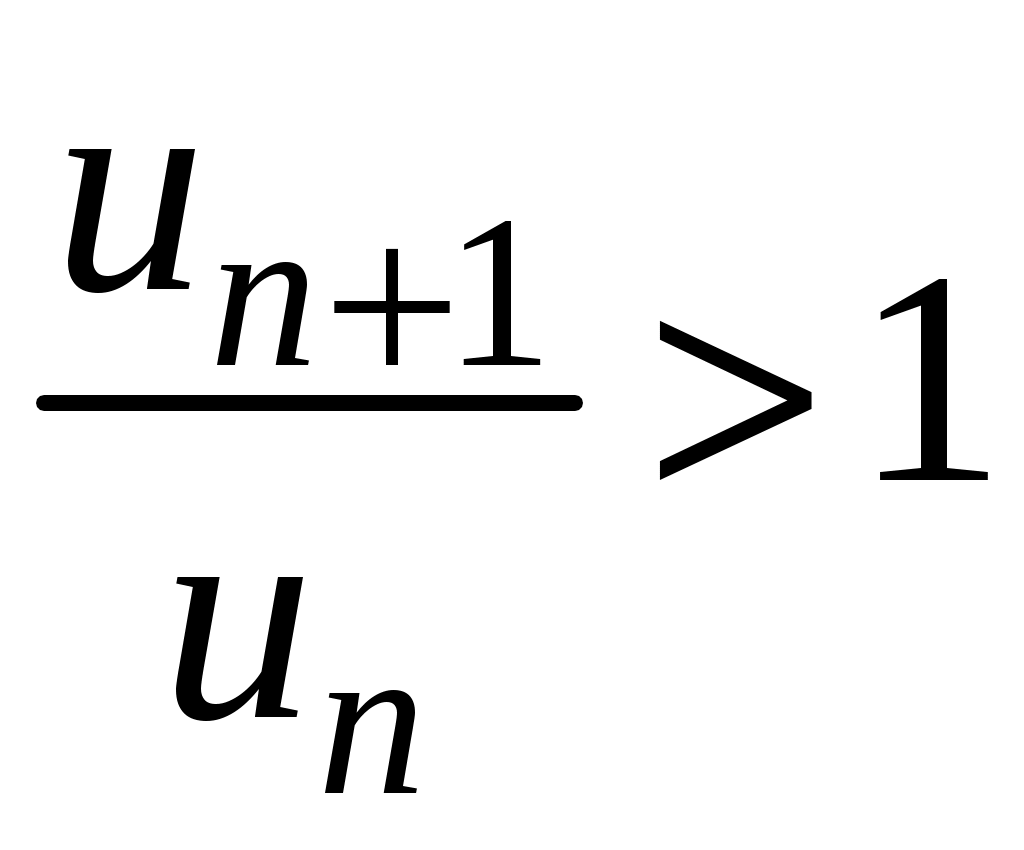 , или , или Замечания. 1). Если 2). Признак Даламбера целесообразно применять, когда общий член ряда содержит выражение вида Пример 4. Исследовать на сходимость ряд Решение: Находим 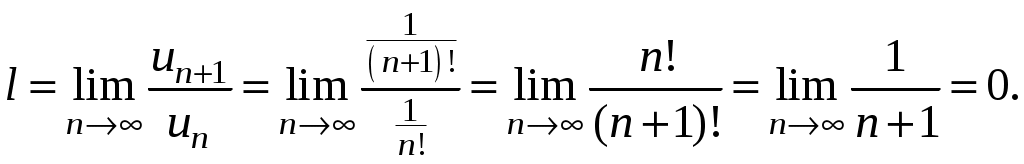 Так как Пример 5. Исследовать сходимость ряда 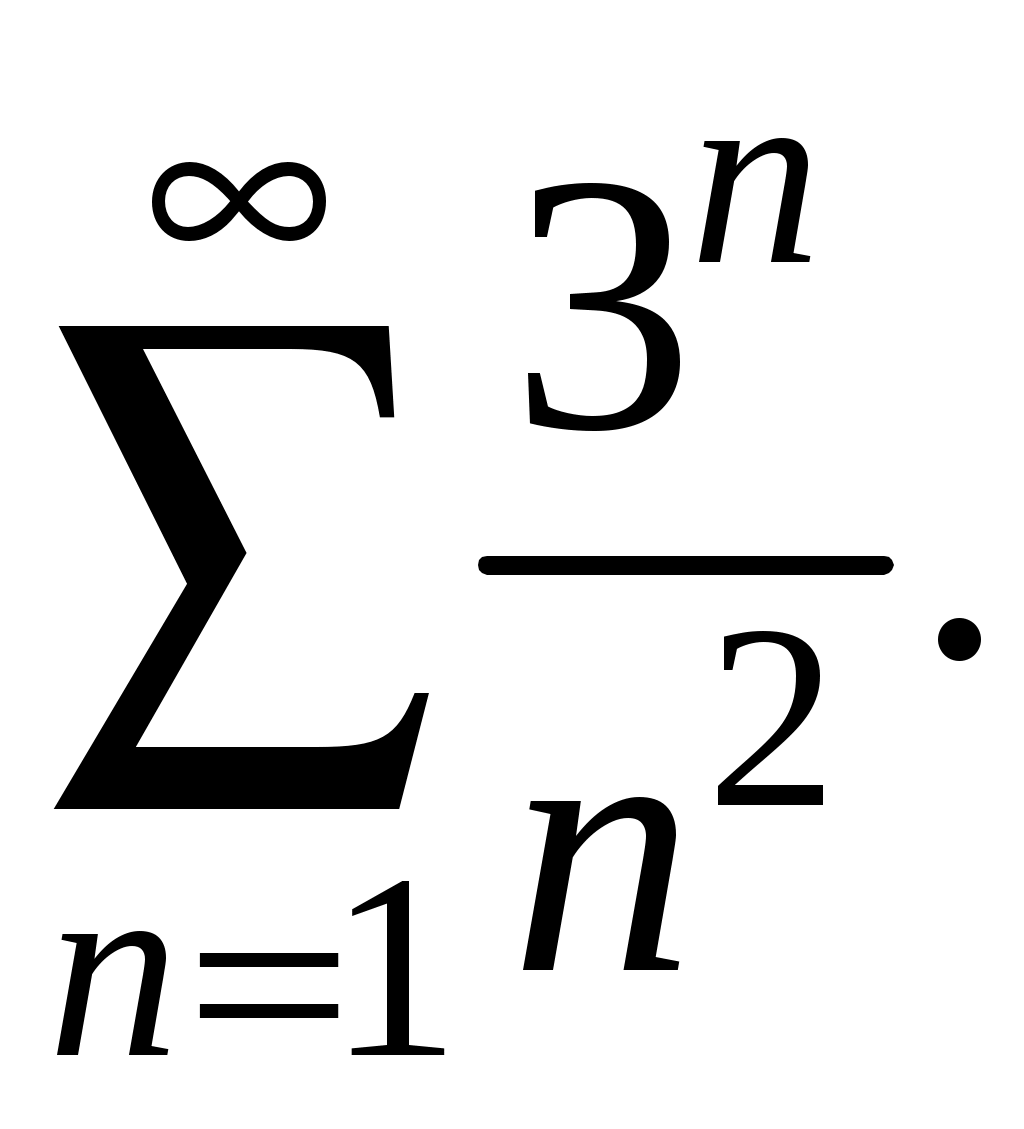 Решение: Вычисляем 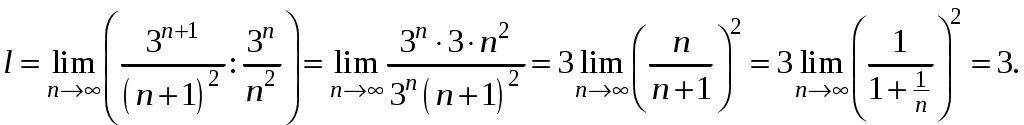 Так как Признаки Коши Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости знакоположительного ряда. Этот признак во многом схож с признаком Даламбера, о чем говорят его формулировка и доказательство. Теорема 4. Пусть дан ряд (6) с положительными членами и существует конечный или бесконечный предел Как и для признака Даламбера, в случае, когда Пример 6. Исследовать на сходимость ряд 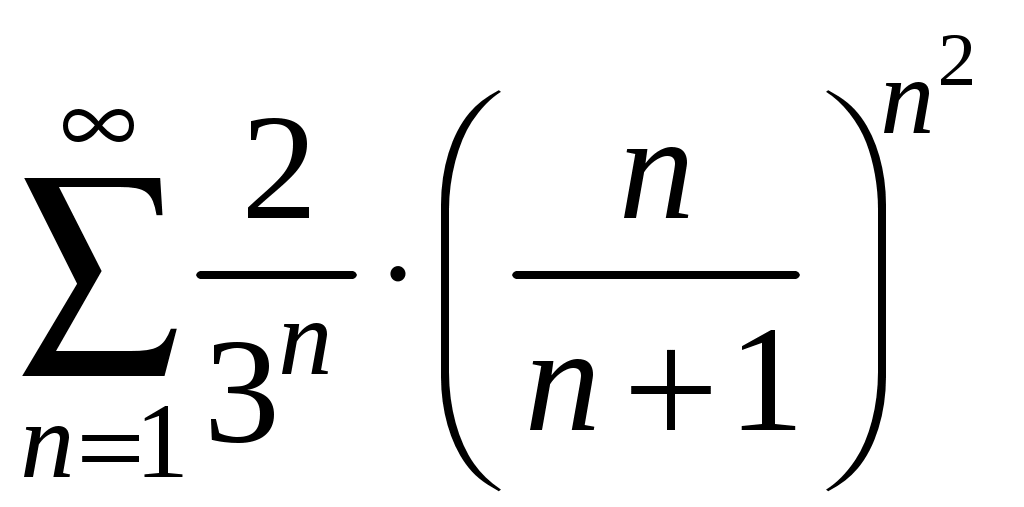 . .Решение: Так как 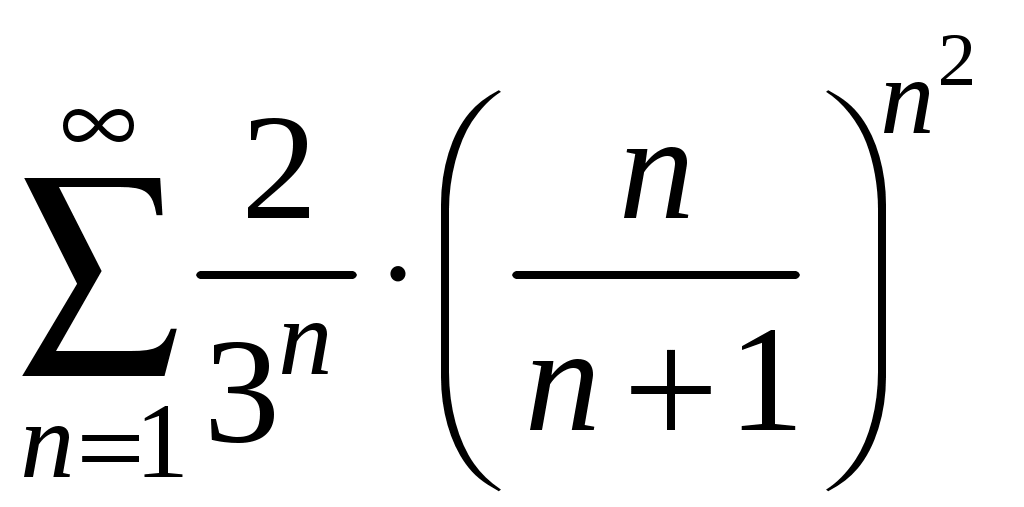 = = 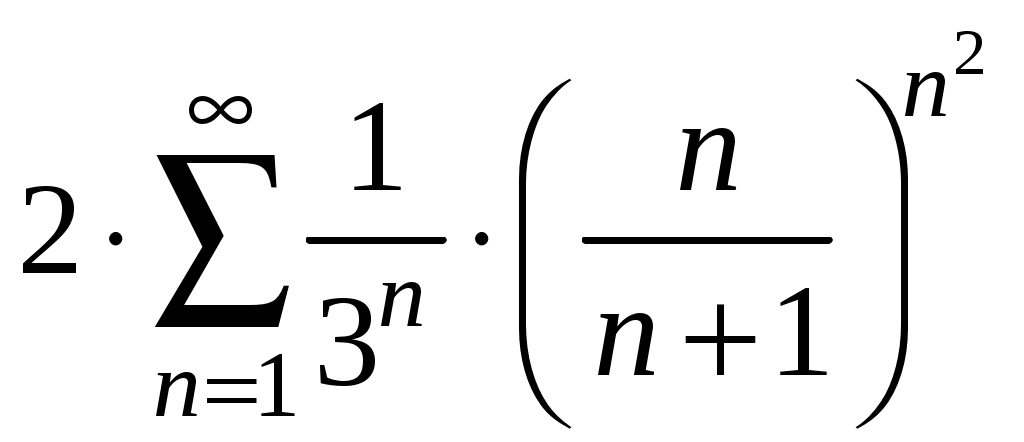 , ,то применим радикальный признак Коши к ряду 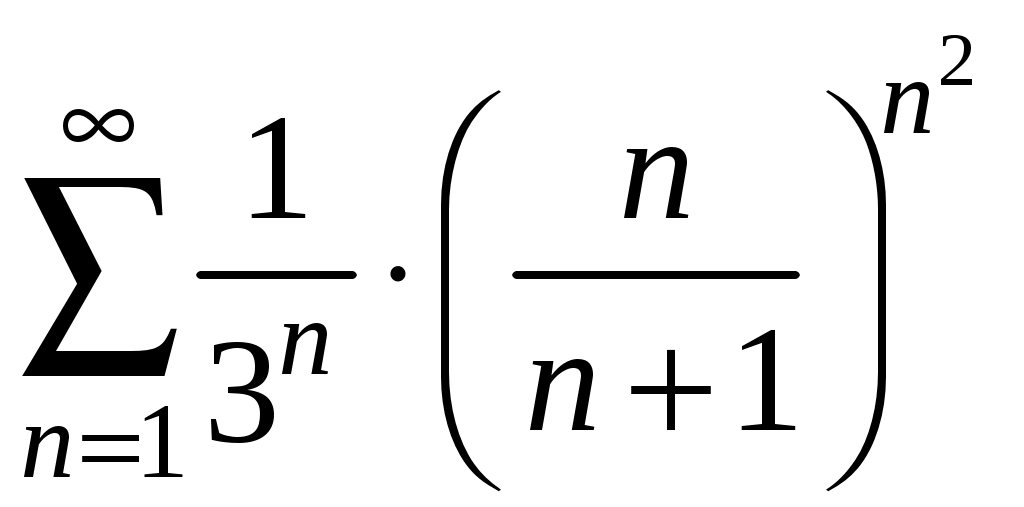 . .Вычисляем 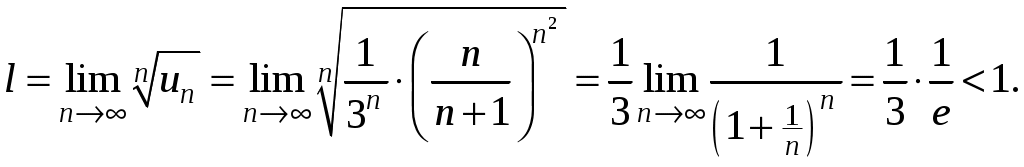 Ряд 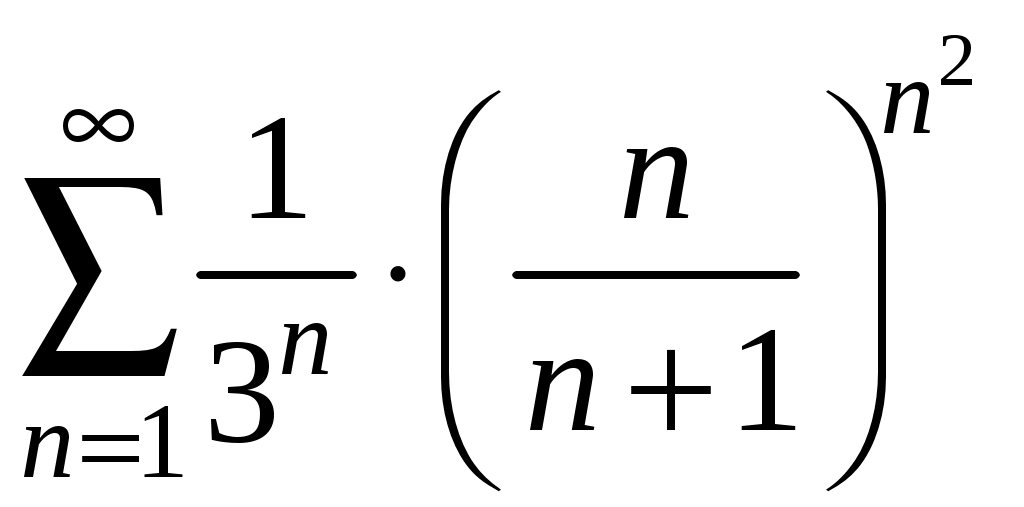 сходится, а значит, сходится и исходный ряд, согласно свойству 1 числовых рядов. сходится, а значит, сходится и исходный ряд, согласно свойству 1 числовых рядов.Теорема 5. Если члены знакоположительного ряда если 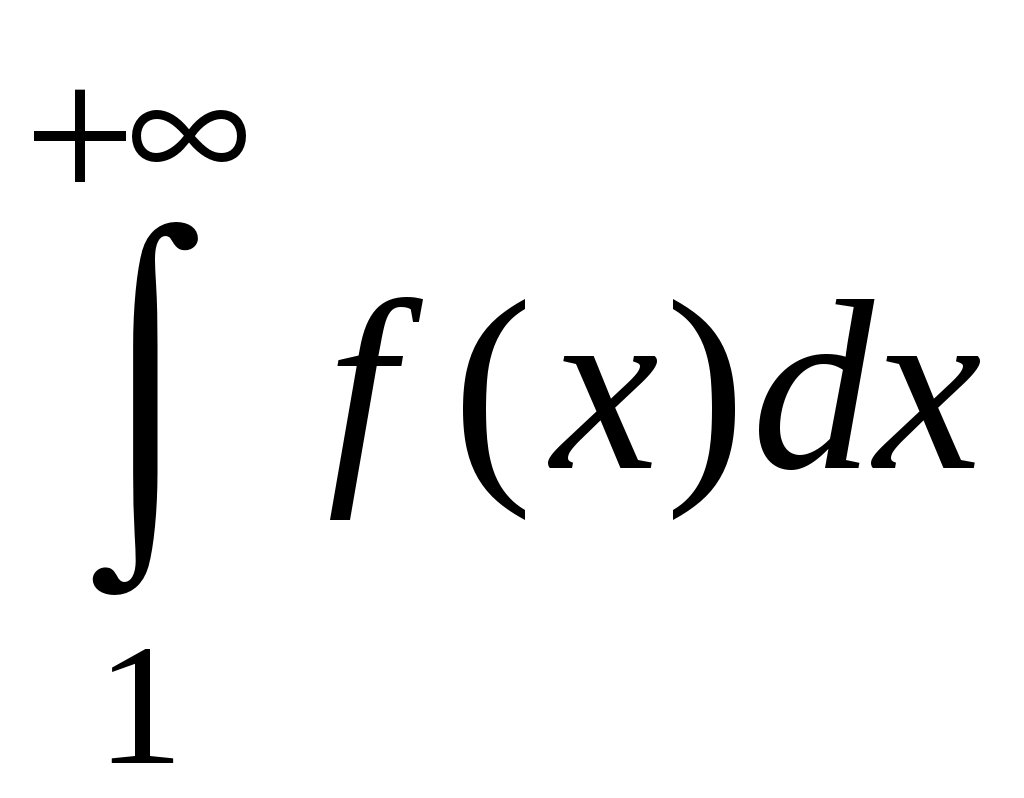 сходится, то сходится и ряд (6); сходится, то сходится и ряд (6);если 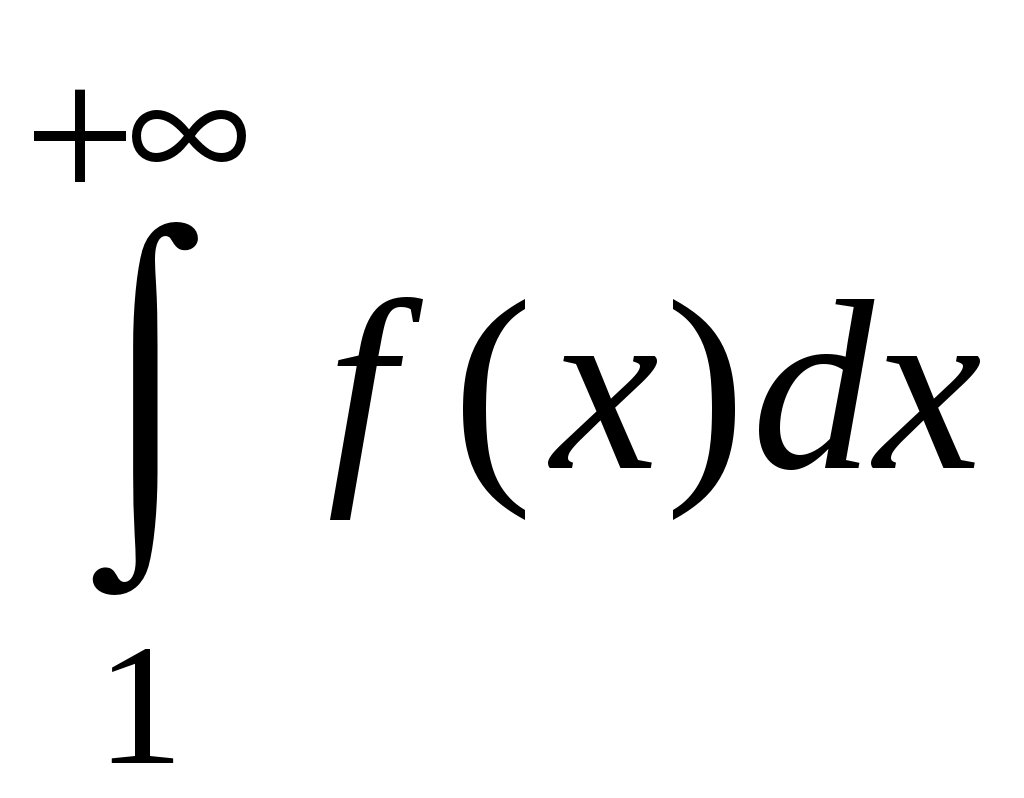 расходится, то расходится также и ряд (6). расходится, то расходится также и ряд (6).Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции  Рис. 1 Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки [1;2], [2;3], … . Учитывая геометрический смысл определенного интеграла, запишем: 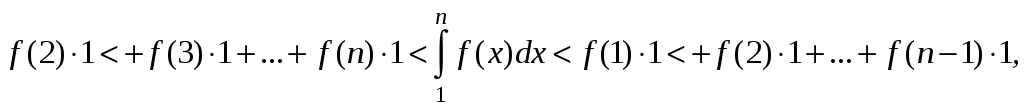 или 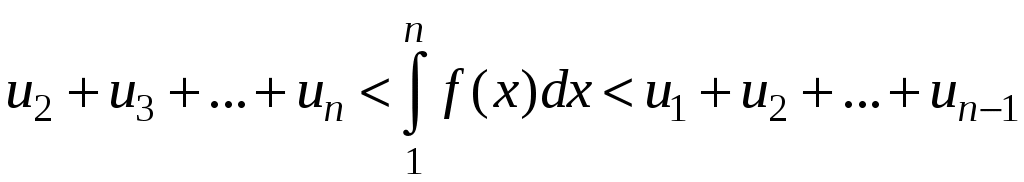 или 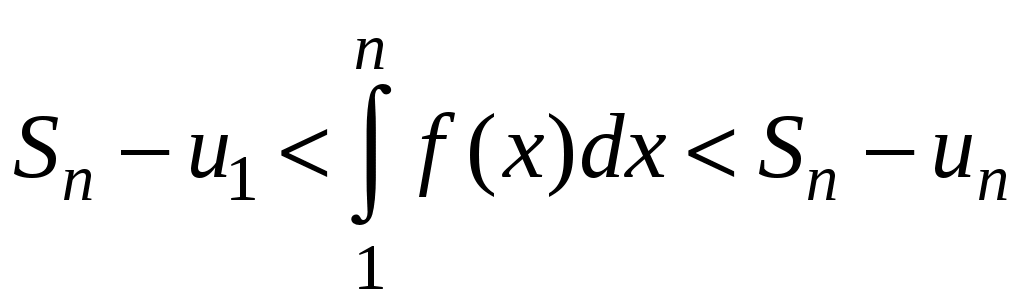 . (8) . (8)Случай 1. Несобственный интеграл 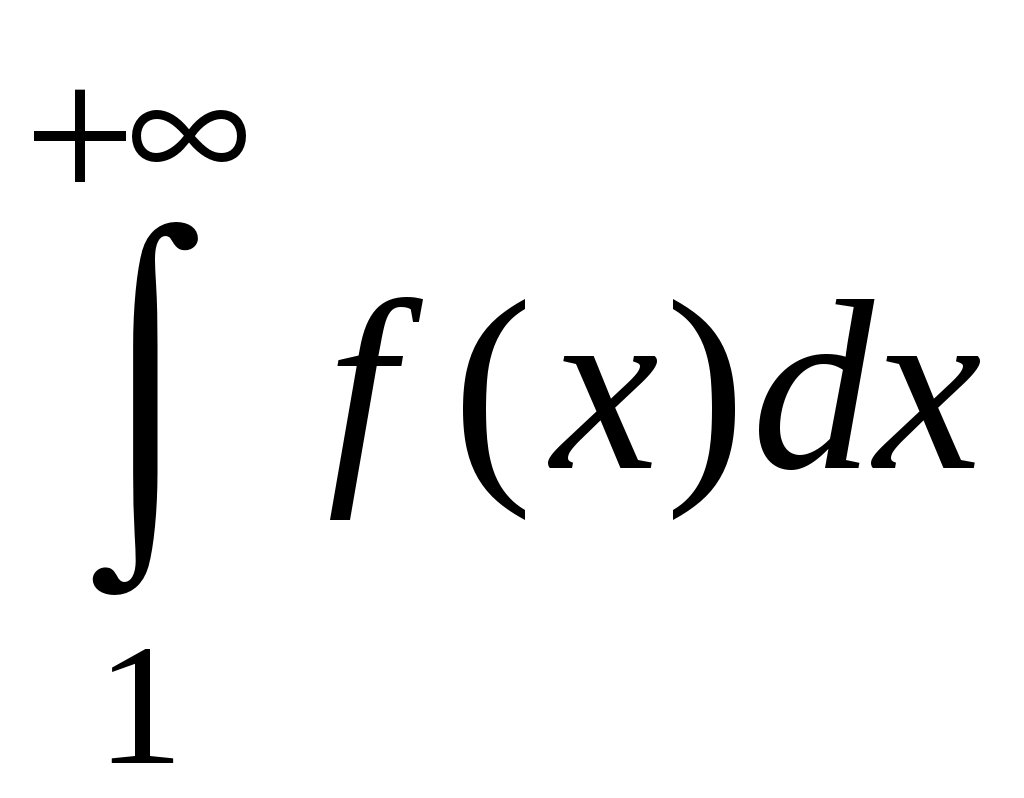 сходится, т. е. сходится, т. е. 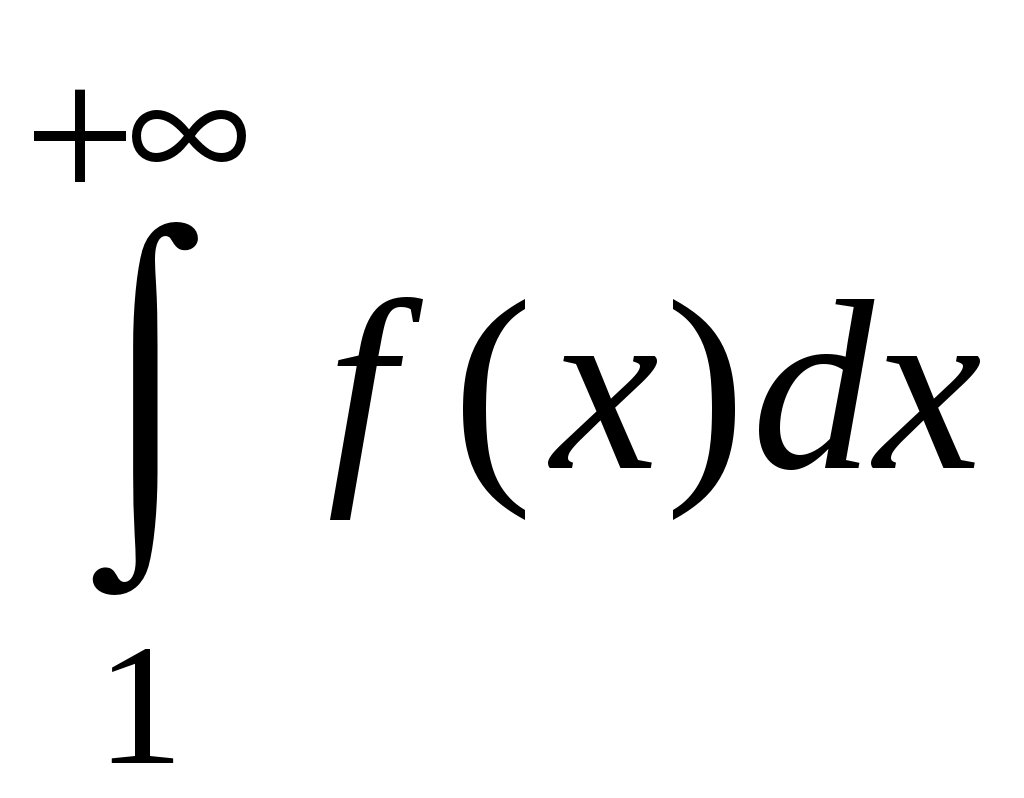 = А. Поскольку = А. Поскольку 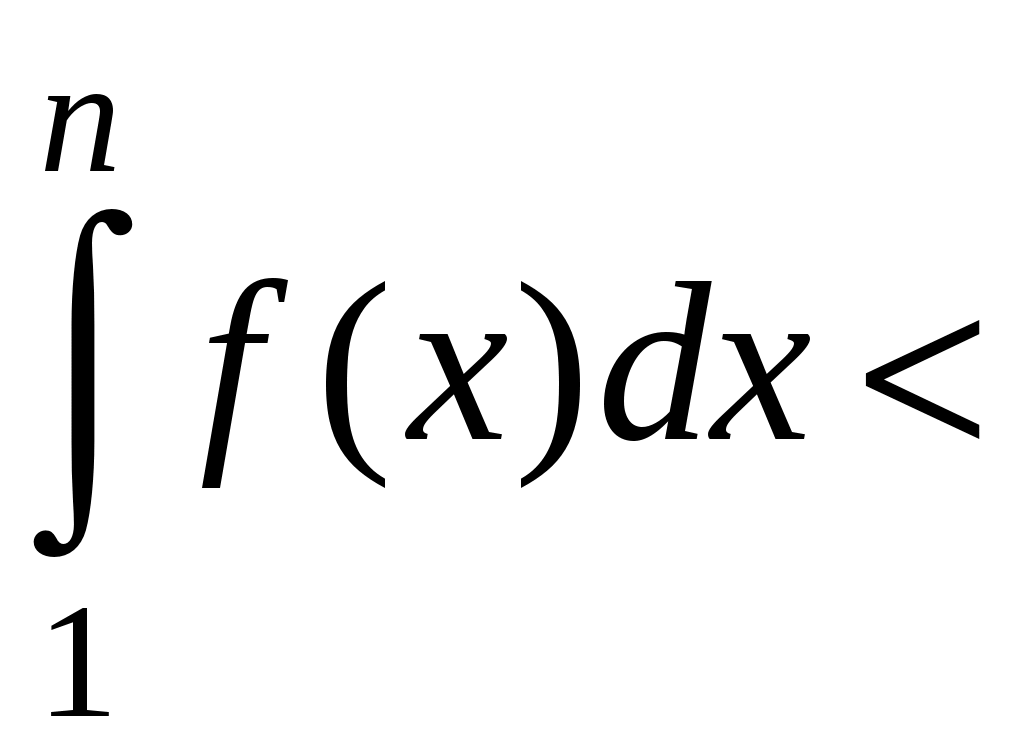 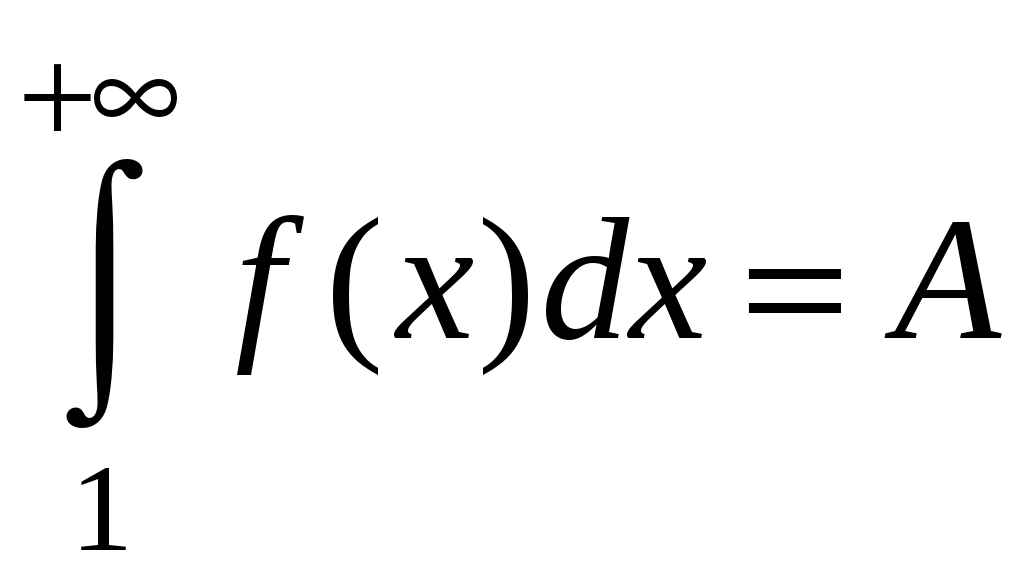 , то с учетом неравенства (8) имеем: , то с учетом неравенства (8) имеем: Случай 2. Несобственный интеграл 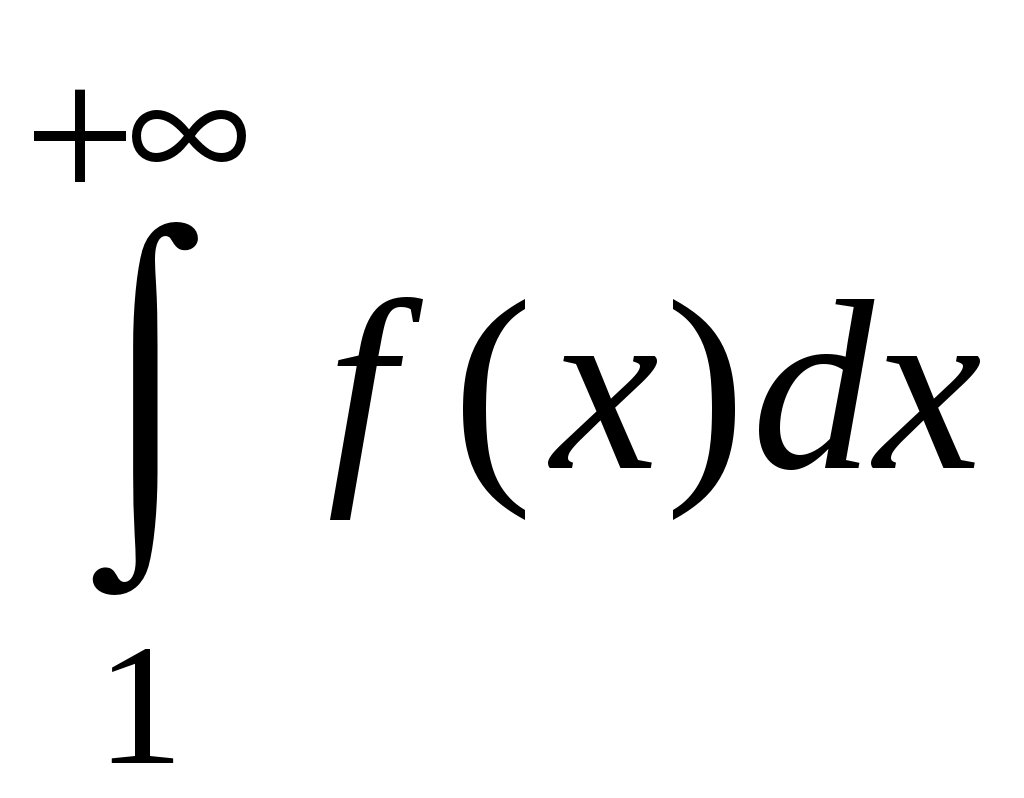 расходится. Тогда расходится. Тогда 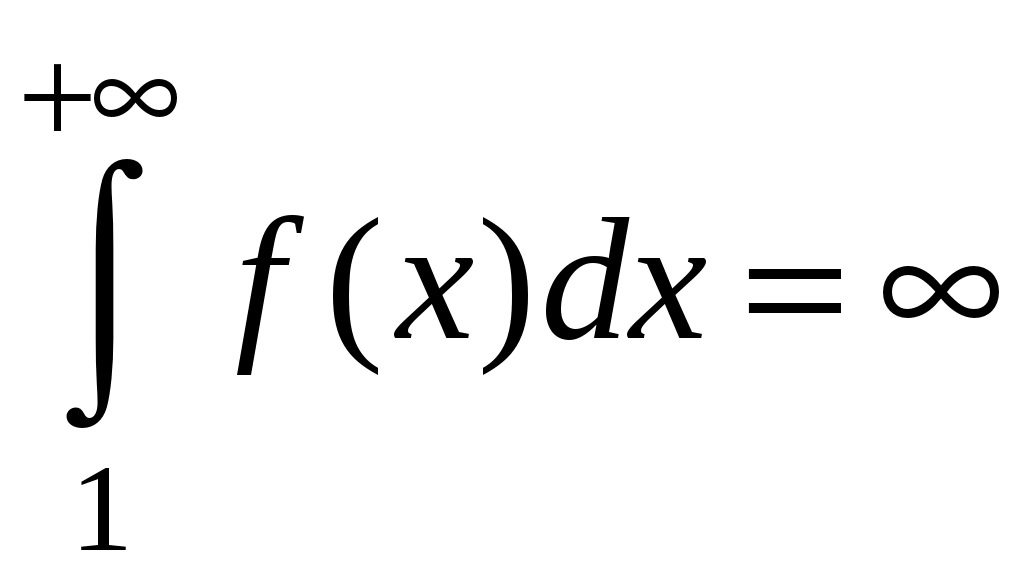 и интегралы и интегралы 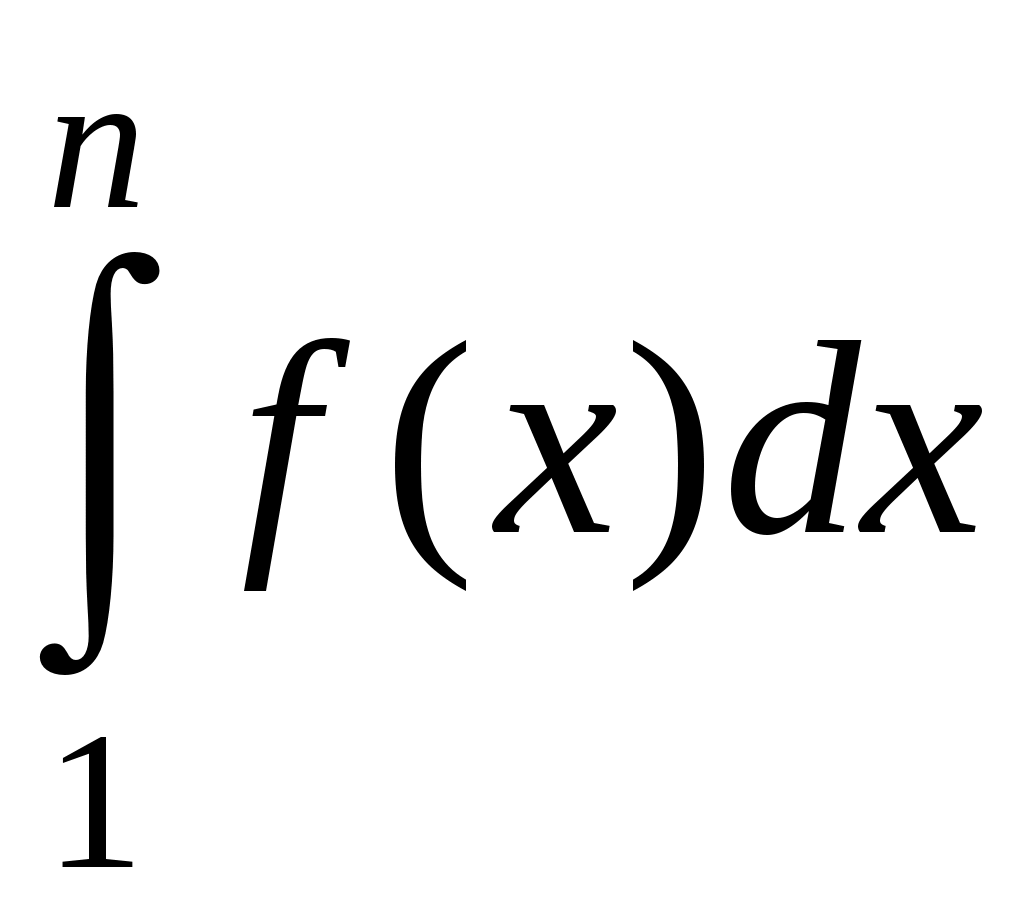 неограниченно возрастают при неограниченно возрастают при 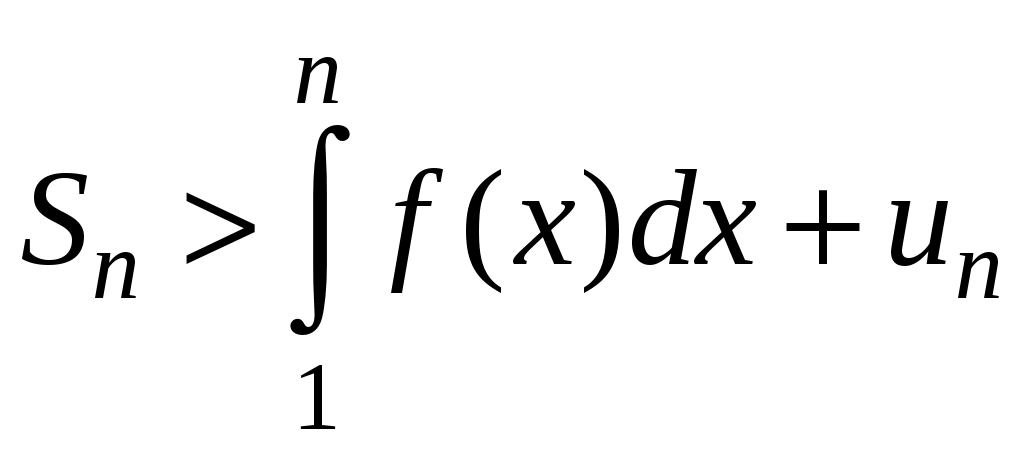 (см. неравенство (8)), получаем, что (см. неравенство (8)), получаем, что Замечание. Вместо интеграла 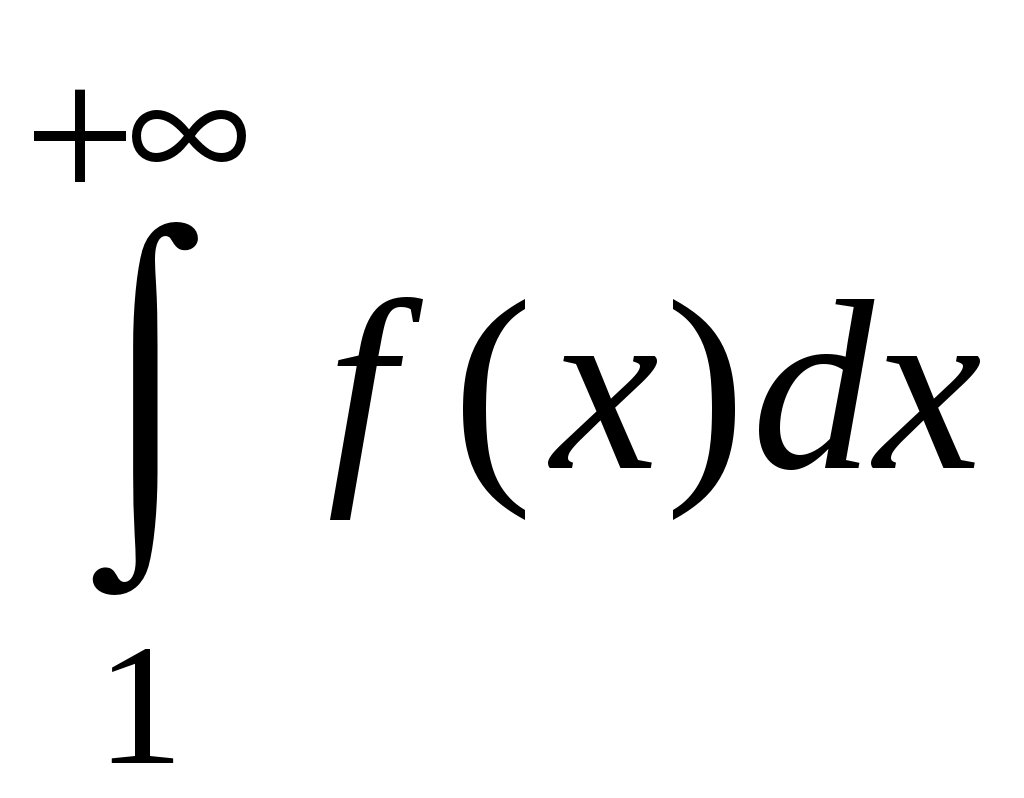 можно брать интеграл можно брать интеграл 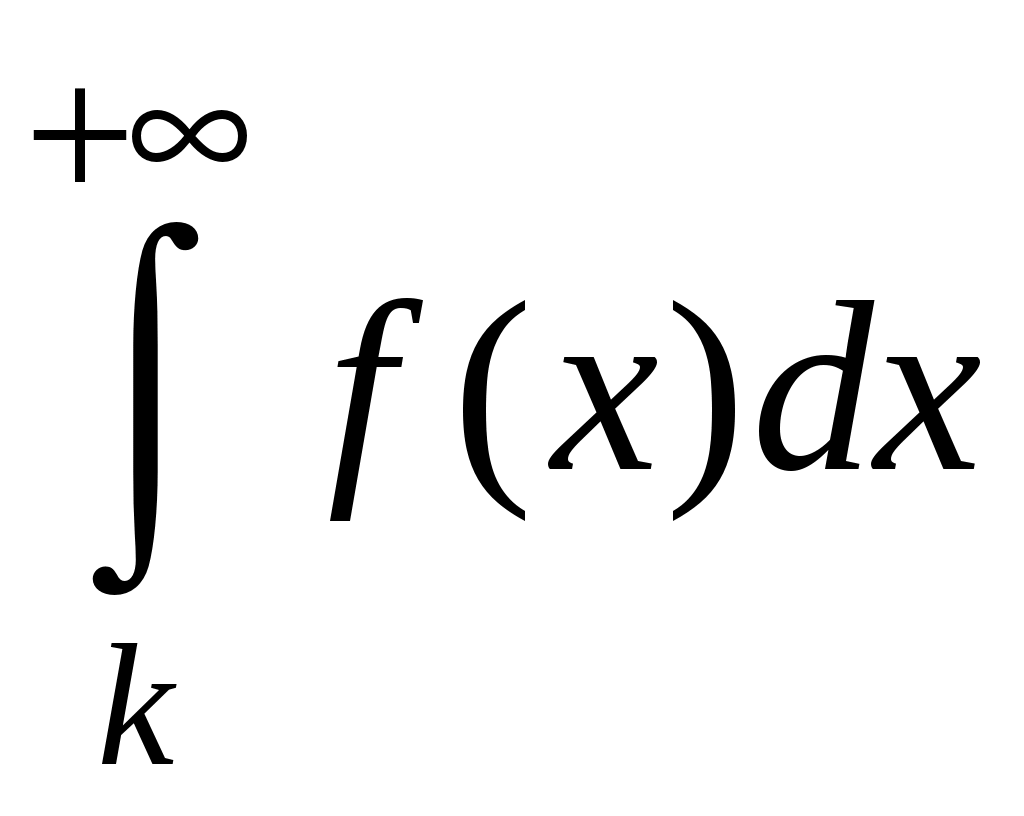 , где , где Пример 7. Исследовать на сходимость ряд 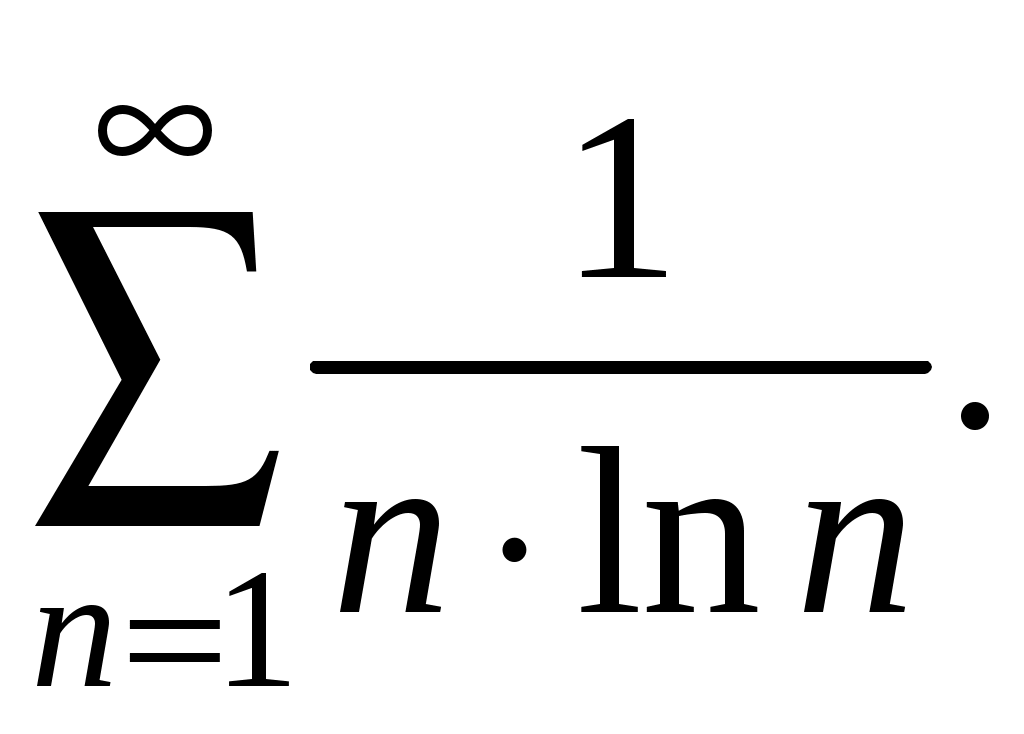 Решение: Воспользуемся интегральным признаком Коши. Функция 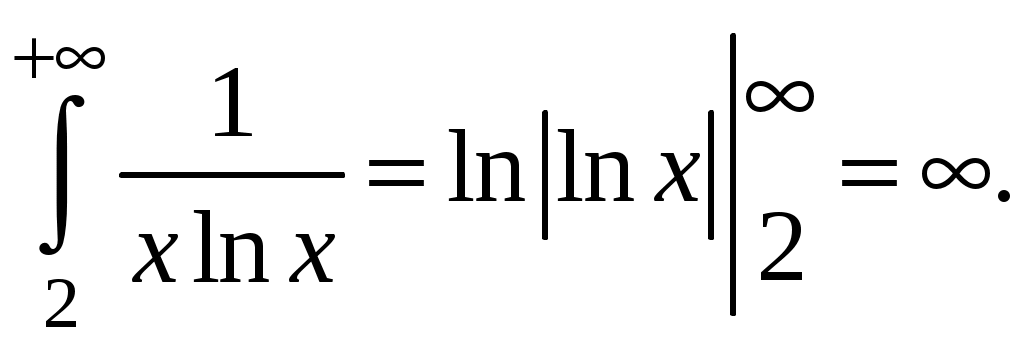 Значит, ряд с общим членом Ряд 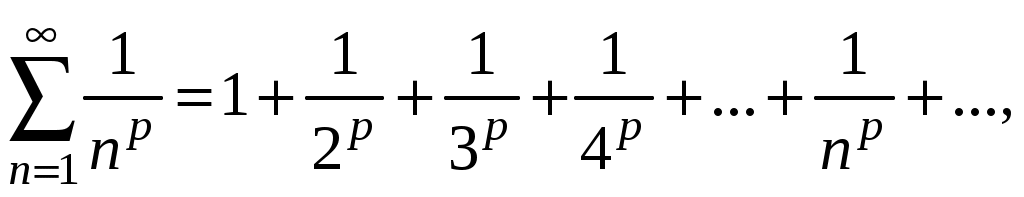 (9) (9)где Для исследования ряда (9) на сходимость применим интегральный признак Коши (признаки Даламбера и Коши ответа о сходимости не дают). Рассмотрим функцию 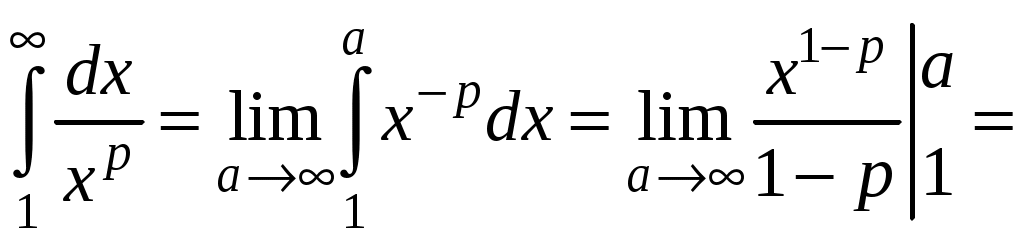 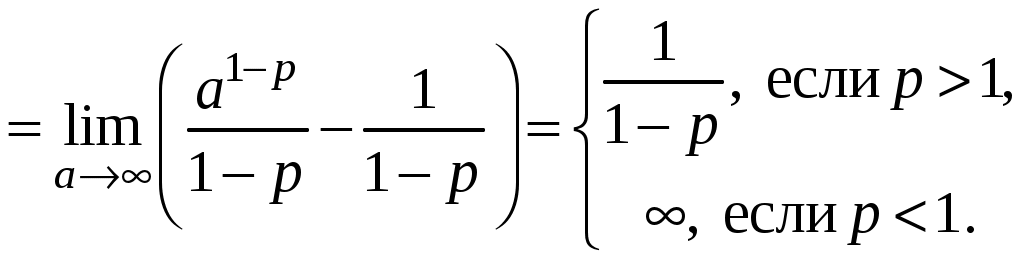 При 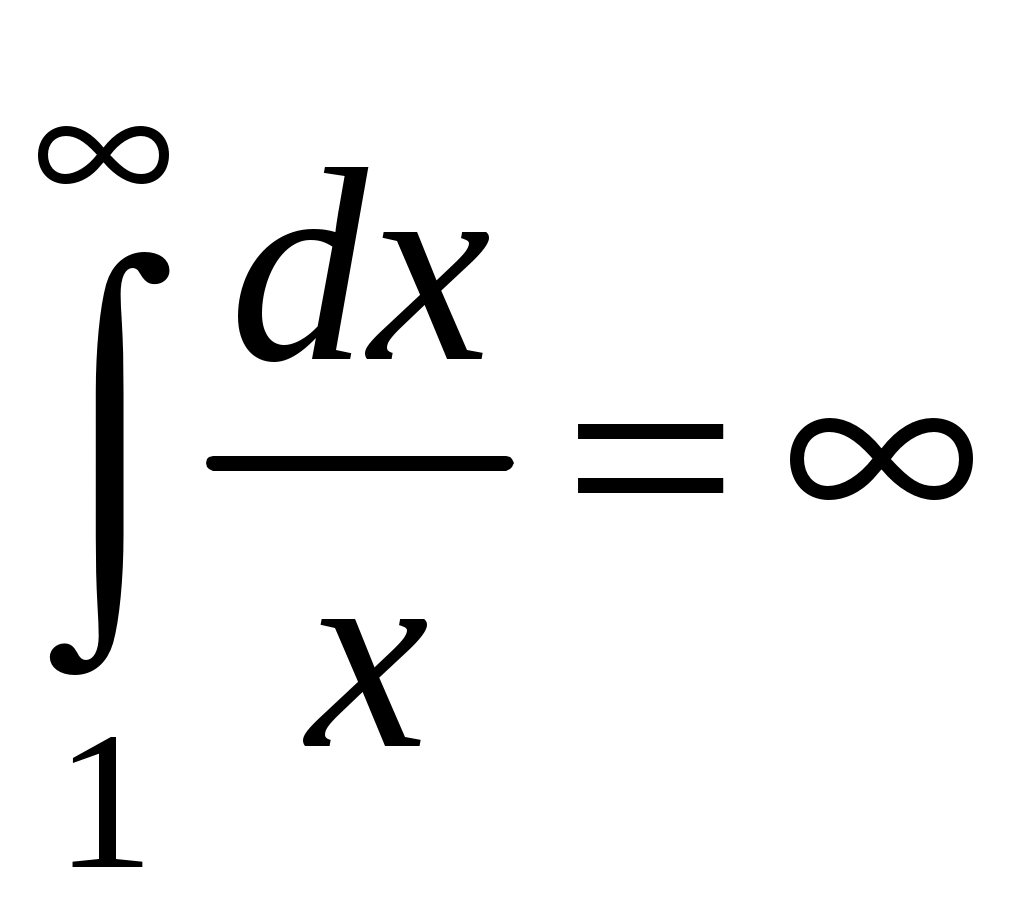 ). Итак, ряд (9) сходится при ). Итак, ряд (9) сходится при В частности, ряд (Полезно знать, что его сумма равна |
