Математика молель. Математическое моделирование в логистике_практика. Лекция по теме и предлагается литература для дополнительного изучения
 Скачать 199.62 Kb.
|
1 2 Контрольные вопросы: 1) Что такое уравнение регрессии? 2) Можно ли использовать данный метод для четырех и более переменных? 3) Какие величины называются моментами второго порядка? 4) В каких областях знаний могут встречаться задачи множественной регрессии? 5) Каким методом определены формулы (3.8)? 6) Что собой представляет результат решения данной задачи? Лабораторная работа № 4 Модель нормально распределенных случайных величин Цель работы: изучение способов компьютерного моделирования случайных величин и определения числовых характеристик по данным наблюдений. Порядок выполнения работы: 1) Изучить теоретические материалы [5,6] и методические указания к выполнению данной работы. 2) Изучить способы компьютерного моделирования непрерывных случайных величин. 3) Составить алгоритм и программу выполнения расчетов характеристик случайной величины. 4) Выполнить программу решения данной задачи для конкретных данных наблюдений. 5) Оформить отчет по данной работе. Теоретические материалы и методические указания Постановка задачи. Случайная величина называется нормально распределенной, если плотность распределения вероятностей имеет следующий вид: 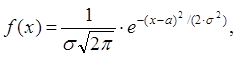 (4.1)где  математическое ожидание,  среднее квадратическое отклонение.Если будут определены характеристики  то считается задача решеной, т.е. определена функция (4.1). Однако точные значения этих параметров невозможно определить, поэтому определяются их оценки. Точечной оценкой математического ожидания является выборочное среднее, а для среднего квадратичного отклонения корень квадратный из выборочной дисперсии.Для определения их используются данные наблюдений, приведенные в таблице 4. Эти данные составляют вариационный ряд. Таблица 4 – Вариационный ряд
Здесь  варианты,  частота появлений вариант;  объем выборки.Алгоритм решения этой задачи имеет следующие этапы: - вводятся значения массивов  и  - вычисление условных вариант  где  ложный нуль,  шаг вариационного ряда;- вычисление условного момента первого порядка  - вычисление условного момента второго порядка 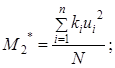 - вычисление выборочного среднего  - вычисление выборочную дисперсию  - вычисление выборочного среднего квадратичного отклонения  Пример. Пусть дан вариационный ряд.
Требуется определить точечные оценки математического ожидания и среднего квадратичного отклонения нормального распределения. Контрольные вопросы: 1) Что такое случайная величина? 2) Какая случайная величина называется нормально распределенной? 3) Что являются основными характеристиками случайной величины? 4) Что такое вариационный ряд? 5) Что такое точечная оценка? 6) Что такое дисперсия случайной величины? Лабораторная работа № 5 Модель определения цены товара на конкурентном рынке Цель работы: изучение одного из популярных методов решения задачи об определении цены товара на конкурентном рынке. Порядок выполнения работы: 1) Изучить теоретические материалы [2,12] и методические указания к выполнению данной работы. 2) Изучить метод решения задачи. 3) Разработать алгоритм решения задачи. 4) Решить задачу с помощью MS EXCEL. 5) Составить программу решения задачи на одном из языков программирования. 6) Отладить программу и выполнить ее для конкретных исходных данных. 7) Получить результат решения задачи в виде таблицы промежуточных значений искомой цены товара. 8) Провести анализ полученного решения. 9) Оформить отчет по данной работе. Теоретические материалы и методические указания Постановка задачи. В экономической теории имеется утверждение о том, что цена товара определяется конкурентным рынком. Она зависит от спроса и предложения на этот товар. Требуется показать процесс установления цены товара на модели. Эконометрическая модель. Пусть рассматривается некоторый рынок определенного товара. Обозначения:  – цена товара,  -функция спроса,  – функция предложения. Для простоты предполагается, что эти функции являются линейными:   , где  – время (период),  – заданные величины, определяющие функции спроса и предложения. Объемы спроса и предложения должны быть одинаковыми:  . Здесь параметр - текущий момент (период торговли) времени, а  показывает предыдущий момент (период торговли) времени. Приведенные выше формулы определяют эконометрическую модель поставленной задачи.Метод решения задачи. В данном случае для решения задачи выполняются простые вычисления объема предложения и спроса, в каждом шаге определяется новое значение цены товара. Алгоритм решения состоит из следующих этапов: - рассматривается координатная система, у которой абсцисса , а ордината  ;- необходимо строить графики функций и ;- задается начальная цена товара  и для нее определяется объем товара по формуле для  ;- из равенства  определяется новая цена товара;- цена товара определяется с определенной точностью; для этого задается либо количество повторения  , либо условие точности:    если выполняется это условие, то процесс решения задачи завершается; в противном случае вычисляется следующее значение цены товара.Пример. Пусть рассматривается пример, для которогозаданы следующие данные:  и начальная цена товара  В результате выполнения программы должно получиться графическое изображение в виде «паутины», поэтому данную модель называют «паутинообразной» моделью определения цены товара в конкурентном рынке. Графики функции спроса и предложения S(p) могут быть изображены в прямоугольной системе координат в зависимости от цены товара : они стремятся к некоторому окончательному значению цены товара и соответствующего объема торговли.Контрольное вопросы: 1) Что такое функция спроса? 2) Что такое функция предложения? 3) Что такое эконометрическая модель задачи? 4) Что является результатом решения данной задачи? 5) Можно ли определить цену товара, не решая данную задачу? Лабораторная работа № 6 Численное решение задачи Коши для обыкновенных дифференциальных уравнений Цель работы: изучение одного из популярных методов решения задачи Коши для обыкновенных дифференциальных уравнений. Порядок выполнения работы: 1) Изучить теоретические материалы [9,12] и методические указания к выполнению данной работы. 2) Сформулировать постановку задачи. 3) Изучить метод решения задачи и разработать алгоритм ее решения. 4) Решить задачу с помощью Excel. 5) Получить решение задачи с помощью компьютерной программы, составленной на одном из языков программирования. 6) Получить результат решения задачи в виде графика искомой функции. 7) Оформить отчет по данной работе. Методические указания по выполнению работы В прикладных задачах часто возникает задача Коши для обыкновенных дифференциальных уравнений. Некоторые из них будут рассмотрены в следующих лабораторных работах. Постановка задачи.Пусть рассматривается дифференциальное уравнение второго порядка 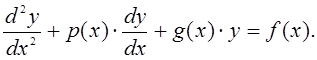 (6.1)В данном уравнении функции 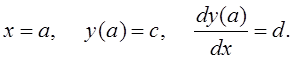 считаются заданными, а функция  является искомой. Требуется найти решение этого уравнения в промежутке  , если заданы следующие начальные условия: (6.2)Метод решения задачи.Для решения этой задачи может быть использован один из методов, в частности, методы Эйлера, Рунге-Кутта и другие. Эти методы используют замену дифференциального уравнения алгебраическими уравнениями. Пусть используется метод Эйлера. Сущность этого метода заключается в следующем. Выбирают маленький шаг 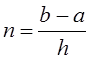 ; а затем промежуток  делится на  равных частей, длина каждой равна  . Точки деления данного промежутка определяются следующей формулой:   .Значения функции  в этих точках  будут обозначены:  Производные искомой функции 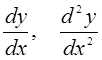 заменяются конечными разностями:  . 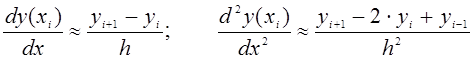(6.3)Используя замену (3), из уравнения (1) можно получить следующую формулу:  (6.4)Начальные условия (6.2) могут быть записаны в следующем виде:  или  (6.5)Итак, вместо дифференциального уравнения получены формулы (6.4) и (6.5); они являются простыми алгебраическими соотношениями. Алгоритм решения задачиможет иметь следующие этапы: 1) вычисление по формуле (6.5) значение  2) начало цикла по параметру   3) вычисление по формуле (6.4) значение  4) переход к следующему номеру  5) проверка конца цикла  если это условие выполняется, то осуществляется переход к этапу 3) для вычисления следующего значения  в противном случае выполняется следующий этап;6) вывод значений  Пример. Пусть рассматривается уравнение:  Для численного решения использованы следующие значения параметров:  Необходимо составить программу решения данной задачи. Результат решения задачи представить в виде графика функции  Контрольные вопросы: 1) Какая задача является задачей Коши? 2) Можно ли решать задачу Коши для системы дифференциальных уравнений первого порядка методом Эйлера? 3) Как определяется погрешность метода Эйлера? 4) В чем сущность метода Эйлера? 5) От какого параметра зависит точность метода Эйлера? 6) В каком виде будут представлены результаты решения данной задачи? 1 2 |
