Насосное оборудование лекции Дерюшев Л.Г.. Насосное оборудование лекции Дерюшев Л.Г. Лекция Тема Введение. Классификация насосов и воздуходувных машин. Краткая история конструирования насосов и воздуходувных машин

• Название: Лекция Тема Введение. Классификация насосов и воздуходувных машин. Краткая история конструирования насосов и воздуходувных машин
• Анкор: Насосное оборудование лекции Дерюшев Л.Г. .doc
• Дата: 06.05.2017
• Размер: 17.95 Mb.
• Имя файла: Насосное оборудование лекции Дерюшев Л.Г. .doc
• Тип: Лекция; #7172
• страница: 2 из 8

Тема: Высота всасывания насоса. Кавитация и борьба с ней

Движение жидкости по всасывающему трубопроводу и подвод ее к рабочему колесу осуществляются за счет разности давлений: Р_А - давления на поверхности воды в приемном резервуаре и Р_вх - давления у входа в колесо насоса.

Уровень воды в источнике по отношению к оси насоса и давление на поверхности воды могут быть различными

1 случай

Забор воды из открытого резервуара. Уровень воды в резервуаре ниже отметки оси насоса (см. рис.а).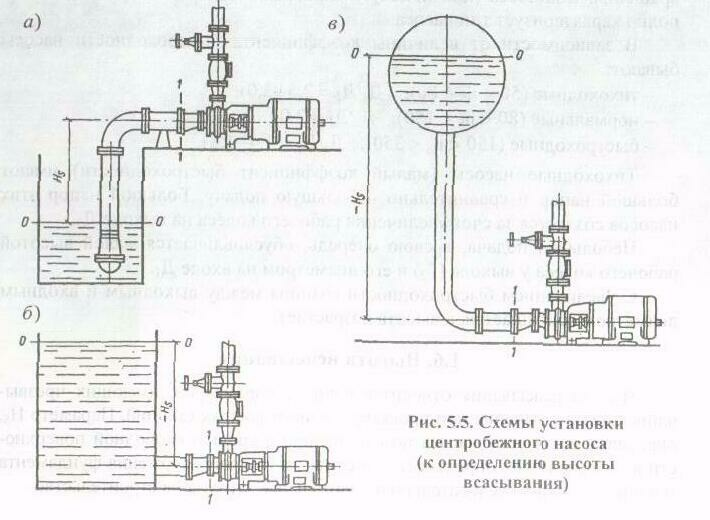


Составим уравнение баланса энергии (уравнение Бернулли) для двух сечений 0-0 и 1-1:

= Н_гвс + + + h_вс,

Н_гвс= - - -h_вс - геометрическая высота всасывания

Н_вак= - - вакуумметрическая высота всасывания

₁ - скорость воды на входе в рабочее колесо;

Р₁ – давлении, создаваемое насосом у входа в рабочее колесо.

Зависимость между вакуумметрической высотой всасывания Н_вак и геометрической высотой всасывания Н_гвс определяется из уравнения:

Н_гвс= Н_вак - - h_вс или

Н_вак= Н_гвс + + h_вс «А»

2 случай

Уровень свободной поверхности воды в резервуаре выше отметки оси насоса (см. рис.б).

В этом случае Н_гвс - геометрическая высота всасывания будет иметь отрицательную величину, и уравнения «А» примут вид:

Н_гвс= + h_вс - Н_вак или

Н_вак = + h_вс - Н_{г. вс}

Отрицательное значение (-Н_гвс) на входе в насос называется подпором. При достаточном подпоре давление на ходе в насос может устанавливаться больше атмосферного на всех режимах его работы.

3 случай

Откачка жидкости из замкнутого резервуара (см. рис.в). В этом случае:

Н_вак= - ₊ ,

где _- некоторое избыточное давление, которое может быть положительным или знакопеременным.

Для того чтобы не происходило отрыва жидкости от лопасти рабочего колеса, необходимо, чтобы давление перед насосом на входе в рабочее колесо было бы больше паров жидкости (≥).

Давление паров жидкости зависит от t^о жидкости (=(t^о)

при t^о = 20^о = 0,24 м

при t^о = 100^о = 10,33 м

при t^о = 0^о = 0,06 м

Равновесное состояние, когда = .

Из уравнения «А» следует, что

Н_гвс= - - - h_вс, т.е.

в этом состоянии наблюдается нормальное движение потока жидкости в рабочем колесе, без отрыва от его лопастей

При  - возникает кавитация.

Кавитация - это явление нарушения сплошности потока жидкости, которое происходит в тех участках, где давление понижается, достигает некоторого критического значения. Чем меньше давление, тем быстрее возникает парообразование жидкости.

Причины кавитации:

а) понижение давление в области рабочего колеса;

б) повышение температуры воды;

в) большая высота всасывания;

г) повышенное сопротивление во всасывающей линии.

Поток воды при входе в рабочее колесо должен изменять свое направление. Поскольку в рабочем колесе жидкость движется с большой скоростью, происходит отжим потока от переднего диска рабочего колеса и прижатие потока к заднему диску. В области «А» давление понижается, а в области «Б» - повышается. Чем больше разность давлений в областях «А» и «Б», тем больше нарушается равномерность движения жидкости.

В области пониженного давления происходит выделение паров жидкости и растворенных в воде газов. В области повышенного давления – обратная картина – конденсация паров и растворенных газов.

Из области пониженного давления воздушные и паровые пузырьки относятся потоком воды в область повышенного давления, где они лопаются и растворяются в воде. При этом возникают точечные гидравлические удары. Чем больше пузырьков, тем больше ударов и их сила. Действуя постоянно на поверхность металла эти удары, разрушают лопасти колеса. Идет процесс коррозии и механического разрушения металла. Неоднородность поверхности металла и наличие жидкости как слабого электролита приводит к появлению местных электрических токов. Места выхода тока в электролит также разрушаются.

В настоящее время кавитация называется процесс появления пустот в потоке жидкости, а весь комплекс – называется кавитационным процессом.

Разрушение же рабочего колеса насоса в результате кавитационного процесса называется кавитацией рабочего колеса. Профессор Н.М. Щапов предложил заменить иностранный термин «кавитация» новым термином, являющимся переводом иностранного слова « опустошение». Однако этот термин не получил распространение.

Задача ставится так, чтобы не допустить работу ц.н. в режиме кавитации.

С этой целью геометрическую высоту всасывания Н_гвс принимают с учетом запаса, а предупреждение кавитации (кавитационный запас)

Н = - - - h_вс - _h_зап,

_ h_зап= ·_h_{мин ,} = 1,11,5 в зависимости от условий работы

Допустимая высота всасывания

Обычно допустимая высота всасывания Н указывается заводом для насосов установленных при атмосферном давлении 10 м.в.с.

Высота над уровнем моря	-600	0	200	300	600	1000	2000
Атмосферное давление, м в.с	11,3	10,3	10,1	10	9,6	9,2	8,4

Н = Н ^кат - 10 + ,

при учете t^о температуры перекачиваемой среды:

Н = Н ^кат - 10 + +0,24 - _h_t ,

Н ^кат - принимается по каталогу

С.С. Рудневым получена формула для определения кавитационного запаса

_ h_мин = 10 (^4/3,

где С – постоянная, зависящая от конструктивных особенностей насоса и называется кавитационным коэффициентом быстроходности (от 800 -1200);

n – число оборотов в минуту.

Для насосов двухстороннего входа Q принимается как для двух насосов, поэтому в формуле Q=.
Лекция № 4

Тема: Основное уравнение центробежного насоса.

Приближенные формулы подачи и напора насоса.

Определение напора насоса по показаниям приборов

Кинематические параметры дви­жения жидкости через рабочие орга­ны лопастного 'насоса оказывают решающее влияние на его энер­гетические показатели. Напор насоса и коэффициент его полезного дей­ствия тесно связаны со значением и направлением скоростей потока жид­кости в межлопастных каналах коле­са. Для установления этой связи воспользуемся теоремой об измене­нии моментов количества движения, которая может быть сформулирована следующим образом: производная по времени от главного момента коли­чества движения системы материаль­ных точек относительно некоторой оси равна сумме моментов всех внешних сил, действующих на эту систему.

Математически теорема за­писывается следующим образом:.

= М
где m— масса рассматриваемой системы ма­териальных точек;

— абсолютная скорость их движения;

r — расстояние до оси.

Удобство теоремы об изменении моментов количества движения в приложении к сплошной среде заклю­чается в том, что с ее помощью динамическое взаимодействие между жидкостью и обтекаемыми поверх­ностями можно определить по ха­рактеру течения в контрольных се­чениях без учета структуры потока внутри выделенного объема.

Применяя теорему к установив­шемуся движению жидкости через рабочее колесо центробежного на­соса между сечениями от входа в колесо до выхода из него, допустим, что при струйном характере течения приращение энергии на этом участке происходит без гидравлических по­терь. Кроме этого, дифференцирова­ние в уравнении (2.36) заменим рассмотрением изменения момента количества движения массы жид­кости за 1 с.

При подаче насоса масса жидкости, участвующей в движении, составит:

т =  Q

Если абсолютная скорость тече­ния жидкости при входе в рабочее колесо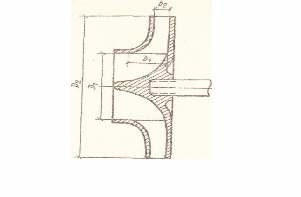


насоса ₁,то момент коли­чества движения в этом сечении относительно оси насоса (рис. 2)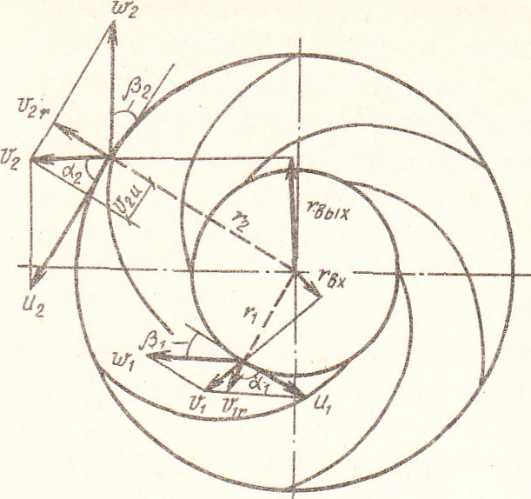



Рис.1. Параллелограммы скоростей потока на входе в рабочее колесо центробежного насоса и на выходе из него

М_к.д.1 = Q₁ r_вх

Момент количества движения на выходе из колеса

М_к.д.2 = Q₂ r_вых

С учетом сделанных допущений уравнение (2) может быть пере­писано в виде

М = М_к.д.2 –М _к.д.1 = Q ( ₂r_вых - ₁r_вх) (1)

Из треугольников скоростей (см. рис. 1) следует:

r_вх = cos₁ и r_вых = сos_2.

Подставляя найденные значения r_вых и r_вхв уравнение (1), имеем:

М = = Q ( ₂cos₂ - ₁cos_1.) (2)

Все внешние силы, действующие на массу жидкости, заполняющей межлопастные каналы рабочего ко­леса, можно разделить на три группы:

1. 
   силы тяжести; как бы ни было расположено рабочее колесо насоса, их момент относительно оси вращения всегда равен нулю, так как рассматриваемый объем представ­ляет собой тело вращения и его центр тяжести находится на оси колеса, т. е. плечо этих сил равно нулю;
   
2. 
   давление на поверхностях контрольных сечений; создаваемые этим давлением силы проходят через ось вращения, и, следовательно,, их момент также равен нулю;
   

3) силы на обтекаемых поверхностях рабочего колеса; главным образом, это воздействие на протекающую жидкость сил давления со стороны лопастей рабочего колеса; участвуют здесь, и силы трения жидкости на обтекаемых поверхностях, однако они сравнительно невелики, и в соответствии со сделанным ранее допущением, их моментом можно пренебречь.

Таким образом, момент внешних сил относительно оси вращения сводится к моменту динамического воздействия рабочего колеса М _р.к. на протекающую через него жидкость, т.е.

М= М _р.к. (3)

В то же время известно, что мощность, передаваемая жидкости рабочим колесом насоса, равна произведению М_р._{к .} С другой сто­роны, та же мощность определяется подачей Q и напором Н_т. Следова­тельно, всегда должно соблюдаться равенство

М_{р. к}= gQH_т (4)

где Н_т— напор, создаваемый рабочим коле­сом насоса.

Поскольку зависимость (5) на­писана без учета каких-либо потерь энергии, то напор Н_т называют также теоретическим.

Преобразуя уравнение (2) с учетом выражений (3) и (4), получаем:

Q (₂ cos₂ - ₁ cos₁) = gQH _т

Так как D_1//2 = u₁ и D_2//2 = u₂ , разделив обе части уравнения на Q окончательно получим:

Н_т = (5)

Зависимость (5), как основное уравнение лопастного насоса, была получена Леонардом Эйлером.


Анализ основного уравнения позволяет установить, что напор центробежного насоса тем больше, чем больше переносная скорость на выходе из рабочего колеса.

Это, в свою очередь, указывает на две принципиально различные возможности повышения напора: путем увеличения выходного диаметра рабочего колеса или за счет увеличения частоты вращения n. Повышение напора может быть также достигнуто уменьшением угла <α₂. Теоретически произведение

u₂ ₂ cos α₂ имеет максимум при α₂=0, однако практически это означает прек-
ращение подачи, поэтому при конструировании рабочих колес центробежных насосов обычно принимают <α₂= 8^о÷ 12°.

При неизменных параметрах по­тока на выходе из рабочего колеса напор насоса, согласно основному уравнению, достигает максимума при условии

u₁ ₁ cosα₁ = 0, (6)

что практически означает cosα₁ =0 или а₁=90^о.

Из параллелограмма скоростей (см. рис. 1) видно, что вектор абсолютной скорости жидкости ₁в этом случае должен быть направ­лен по радиусу, поэтому условие (6) обычно называют условием радиального входа.

Поскольку при а₁=90^о проекция абсолютной скорости на направление переносной скорости равна нулю (₁= 0), то условие радиального входа также означает, что жид­кость подводится к рабочему коле­су без предварительного закручива­ния. Уравнение Эйлера при этом принимает вид:

Н_т= u₂₂ · cos a₂ / g(7)

Применительно к осевым насосам, имея в виду, что на любом радиусе переносные скорости на входе и выхо­де одинаковы (u₁=u₂ = u),можно написать:

Н_т= u( ₂•cos a₂ -₁ · cos a₁ / g.(8)

Уравнение (8) показывает, что теоретический напор осевого насоса пропорционален произведению пере­носной скорости и разности, составля­ющих абсолютной скорости потока в направлении переносного движе­ния.

При отсутствии предварительного закручивания жидкость поступает в межлопастные каналы колеса в осе­вом направлении, следовательно, ₁ • cos a₁ = _1u = 0. В этом случае основное уравнение осевого насоса имеет вид:

Н_т= u  _2u / g.(9)
÷Приближенные формулы подачи и напора насоса

Приближенная формула подачи насоса:

Q =_{об }  _z D₂b₂₂ sin₂ (10)

где D₂ и b₂ - диаметр и ширина рабочего колеса ,

₂ - относительная скорость на выходе из колеса,

₂ – угол наклона лопасти колеса к горизонту.

_об- объемныйкоэффициент полезного действия.

 _z = (D₂ - z)D₂ - коэффициент стеснения потока за счет наличия Z лопастей в насосе

 - толщина лопасти колеса.

Напор насоса:

Н = _г u₂₂ · cos a₂ / g (11)

где _г- гидравлическийкоэффициент полезного действия

Лекция № 5