Насосное оборудование лекции Дерюшев Л.Г.. Насосное оборудование лекции Дерюшев Л.Г. Лекция Тема Введение. Классификация насосов и воздуходувных машин. Краткая история конструирования насосов и воздуходувных машин

• Название: Лекция Тема Введение. Классификация насосов и воздуходувных машин. Краткая история конструирования насосов и воздуходувных машин
• Анкор: Насосное оборудование лекции Дерюшев Л.Г. .doc
• Дата: 06.05.2017
• Размер: 17.95 Mb.
• Имя файла: Насосное оборудование лекции Дерюшев Л.Г. .doc
• Тип: Лекция; #7172
• страница: 3 из 8

Тема: Законы подобия насосов. Коэффициент быстроходности

Подобие насосов. Сложный характер движения перекачиваемой жидкости в рабочих органах ло­пастных насосов приводит к тому, что задача создания современных высокопроизводительных машин, от­вечающих сложному комплексу тре­бований , решается, наряду с расчетно-теоретической разработкой конструкций их про­точной части, путем проведения испытаний в лабораторных и натур­ных условиях. При проектирова­нии новых насосов используются также опытные данные, получаемые в процессе эксплуатации анало­гичных насосов на действующих станциях.

Предварительное определение расчетных параметров проектируе­мой машины, исследования рабочих режимов на моделях и распро­странение полученных результатов на натурные насосы возможно на основе теории о механическом по­добии движения реальной жид­кости. Главное положение этой теории заключается в необходи­мости выполнения условий геометри­ческого, кинематического и дина­мического подобия.

Геометрическое подобие в гид­ромеханике означает подобие всех поверхностей, ограничивающих и направляющих поток. При моде­лировании гидравлических машин два насоса могут быть названы подобными, если все линейные раз­меры одного из них (модель) в одинаковое число раз меньше или больше соответствующих размеров другого (натура). Математически геометрическое подобие сравниваемых насосов определяется посто­янством линейного коэффициента подобия:

Mi = D_H/D_M = bн/bм =... = const, (1)

где = D_H, D_M, bн, bм — соответственно диаметр и высота рабочих колес модельного и натур­ного насосов.

Геометрическое подобие означает также постоянство отношений лю­бых других размеров у модели и натуры.

Очевидно, что в осевых насосах геометрическое подобие подразуме­вает равенство углов установки лопастей рабочего колеса: _м = _н.

Строго говоря, геометрическое по­добие означает также подобие шеро­ховатостей обтекаемых потоком по­верхностей и зазоров между дви­жущимися и неподвижными деталя­ми насосов. Следовательно, для пол­ного его соблюдения необходимо, чтобы относительные шероховатости /D и относительные зазоры / D , где  и  — соответственно экви­валентная абсолютная шерохова­тость и зазор, были одинаковыми. Но выполнение этого требования в практике моделирования гидравли­ческих машин возможно далеко не всегда. Действительно, при значе­ниях М_l = 20÷30 какие-либо высту­пы или неровности размером 1—2 мм точно воспроизвести на модели не удается.

Кинематическое подобие в общем виде означает, что безразмерные по­ля скоростей в рассматриваемых потоках должны быть одинаковы, т. е. отношения скоростей всех соответствующих частиц жидкости, участвующих в движении, должны быть равны между собой, а траек­тории движения в сравниваемых гид­равлических системах — геометри­чески подобны. Применительно к насосам это, в частности, означает подобие параллелограммов скоро­стей в соответствующих точках пото­ка во всех элементах проточной части двух геометрически подобных машин, ра0отающих в одинаковых режимах. Математически условия кинематического подобия могут быть выражены в виде ряда отношений:

_н/_м = _н /_м = u_н /u_м =n_нD_н /n_мD_м = ...сonst

Для соблюдения требований ки­нематического подобия необходима также выдерживать постоянным от­ношение скорости протекания жид­кости к скорости движения вращаю­щихся деталей, т. е.

_м/ u_м = _н/ u_н = сonst

Используя геометрическое подо­бие, из которого следует, что   Q/D² и u /  nD ^, получаем еще одно условие кинематического подо­бия, представляющее чрезвычайно большой практический интерес при моделировании насосов:

Q_м / n_м D_м =Q_н / n_н D_н = сonst(2)

Динамическое подобие кроме соб­людения условий геометрического и кинематического подобия означает пропорциональность сил, действую­щих в соответствующих точках пото­ка. При отнесении к этим силам дав­ления, вязкости, сил тяжести и инер­ции динамическое подобие в общем виде обусловливается, как это хоро­шо известно, равенством чисел Эйле­ра, Рейнольдса, Фруда и Струхаля:

Eu= P/(²); Re =l/, Fr= ² /gl, St= t/l (3)

где l— характерный линейный размер;  — кинематическая вязкость жидкости; t— вре­мя.

Все эти критерии являются опре­деляющими лишь тогда, когда они выражены через исходные величины, задаваемые в начальных и граничных условиях. В противном случае каж­дый из определяющих критериев перейдет в неопределяющие или зависимые критерии. В частных за­дачах гидромеханики число опре­деляющих критериев, как правило, меньше указанных четырех.

В практике моделирования гид­равлических машин очень большое значение имеет критерий подобия Эйлера. Применительно к рассматри­ваемым условиям он может быть вы­ражен следующим образом:
Еu= P/(²)=gH /(²). (4)

Заменяя скорость пропорцио­нальным отношением подачи к квад­рату диаметра рабочего колеса, по­лучим:

Еu= gHD⁴ /(Q²).

Следовательно, условие подобия может быть записано в виде:
Q_н / D_н² =Q_м / D_м² 5)

Уравнение (5) устанавливает зависимость между двумя основными энергетическими параметрами (по­дачей и напором) модельного и на­турного насосов.

Соблюдение условия равенства чисел Рейнольдса в натуре и на модели при решении практических задач осуществимо далеко не всегда. Теоретический анализ возможности выполнения этого условия показы­вает, что кинематическая вязкость жидкости модельного потока _м должна быть меньше кинематической вязкости натурного потока  _н в М раз. При испытании модели осевого насоса, имеющего в натуре рабочее колесо диаметром D_н = 4 м, на экспериментальной установке с колесом диаметром D_м = 0,2 м коэф­фициент подобия будет равен 20. Тогда кинематическая вязкость жид­кости модельного потока для соблю­дения равенства Re_м = Re_н должна быть меньше кинематической вяз­кости воды в 89,5 раза, а капельных жидкостей столь малой вязкости в природе не существует.

Формулы пересчета. Принимаем, что геометрически подобные друг другу рабочие колеса однотипных на­сосов диаметрами D_ми D_н вра­щаются с частотами n_н иn_м , соответственно создавая при этом напоры Н_м и Н _н и обеспечивая подачи Q_м и Q_н.

Из основного., уравнения для условий безударного входа имеем, что при n _м и D _м напор насоса

H_м = k_м_г u_2н_2н ·· cos a_2м / g

и соответственно при n_н и D _н

H_н = k н _г u_2м_2м·cos a_2н / g

Отношение этих напоров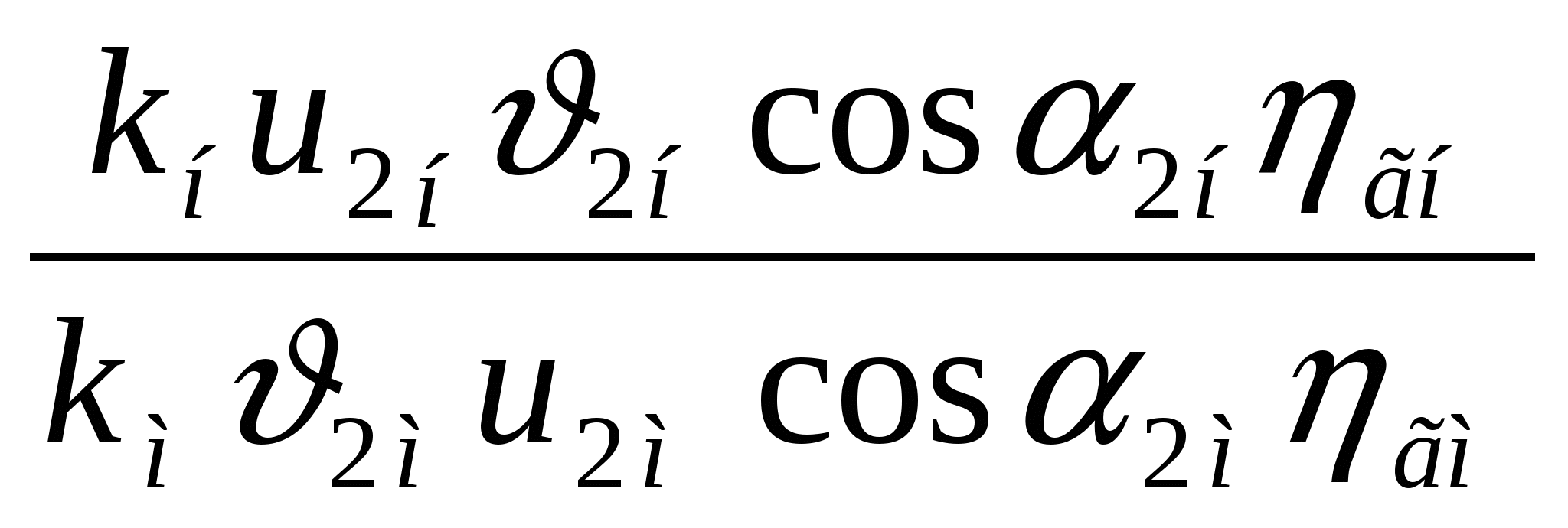

=

Исходя из условий геометрическо­го подобия, можно считать, что k_н = k_м, а подобие параллелограммов скоростей, вытекающее из условий кинематического подобия, означает равенство углов: _2н = _2м. Отноше­ние скоростей u₂. и ₂, согласно математическому выражению усло­вий кинематического подобия пропорционально от­ношению произведений nD. Следовательно, если подобные друг другу рабочие колеса насосов будут вращаться с различной часто­той, то для создаваемых ими напо­ров можно написать соотношение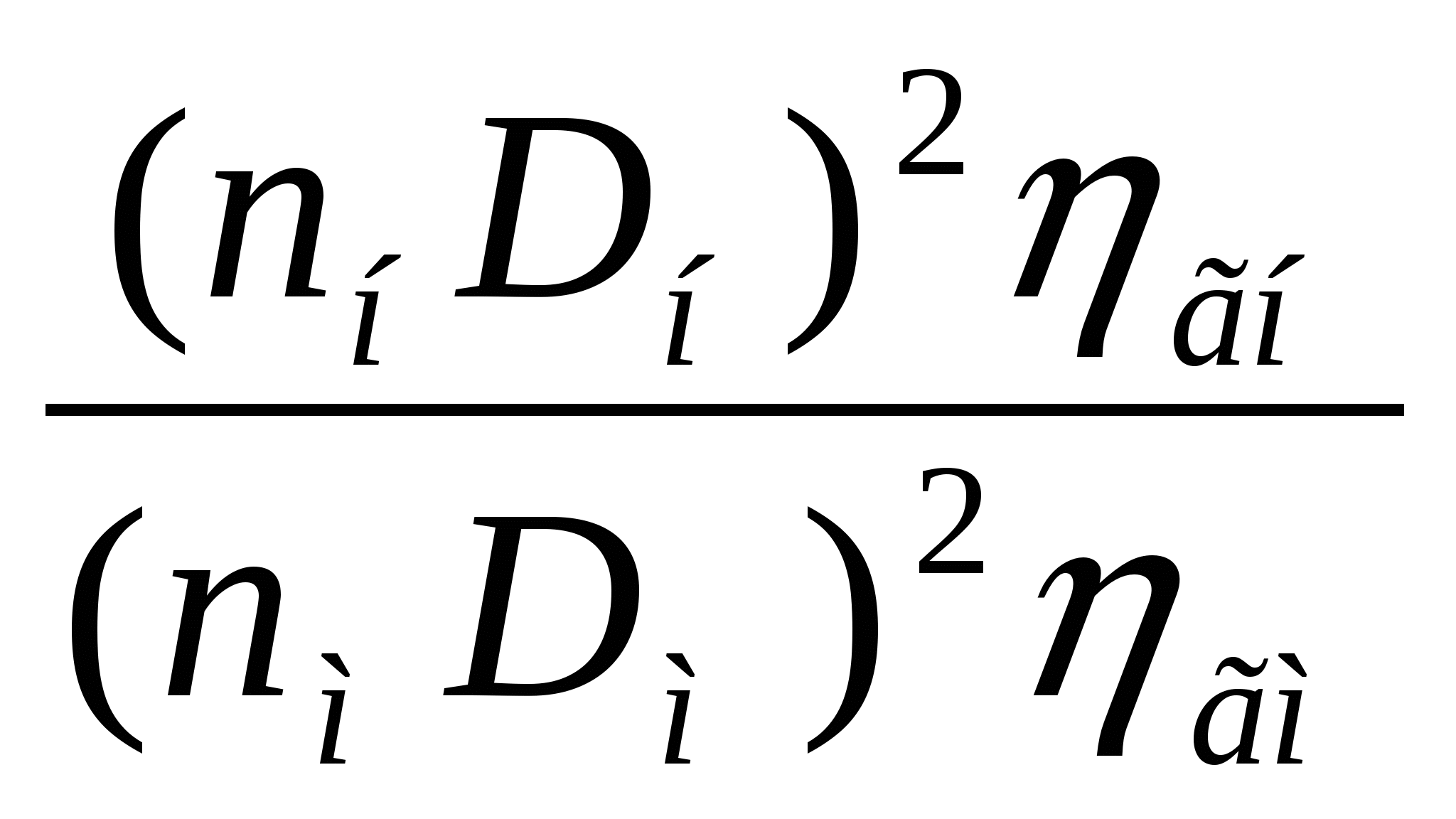

= (6)


Как уже известно, подача насоса из­меняется пропорционально измене­нию площади выходного сечения рабочего колеса и радиальной со­ставляющей абсолютной скорости на выходе, тогда =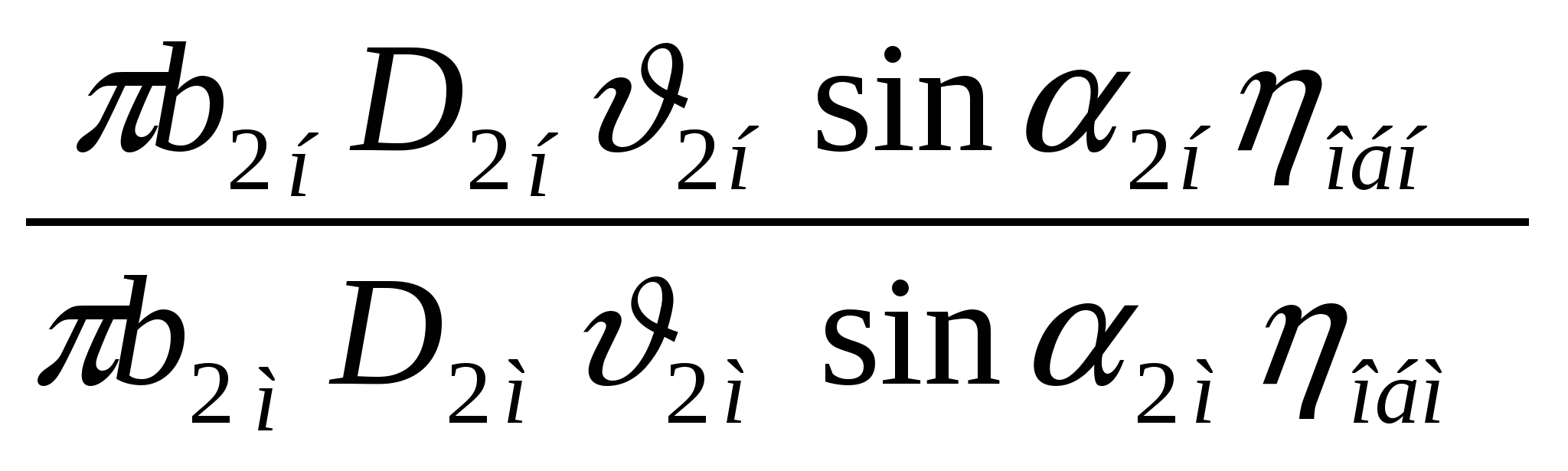
Поскольку рабочие колеса рассматриваемых насосов геометри­чески подобны, т. е. b_2н/b_2м = D _2н / D _{2м ,} то в общем случае с учетом условий кинематического подобия

a_{2н =} a_2ми ==

можно написать:
(7)

Мощность насоса изменяется пропорционально произведению QH. Подставляя вместо Q и Н со­ответствующие величины из урав­нений ( 6) и (7), имеем:

(8)
Уравнения (6) — (8), полу­ченные на основе подобия лопастных насосов, называют формулами пере­счета. Эти формулы дают возмож­ность с большой точностью рассчи­тать основные параметры проекти­руемого насоса, если известны пара­метры насоса, геометрически ему подобного. Наконец, формулы пере­счета дают возможность после испытания насоса при одной частоте вращения определить его параметру для другой частоты.

Для пересчета КПД насоса с модели на натуру был предложен ряд формул, но широкого распрост­ранения они не получили. Причина этого заключается в том, что лопастных насосов значение КПД в большой мере определяется объ­емными и механическими потерями.Поэтому пересчет КПД с модели на натуру без разделения его на составляющие не оправдывает себя.

Как отмечалось ранее, самым трудным является определе­ние гидравлического КПД. Совре­менные методы его вычисления сво­дятся к использованию зависимости _г от размеров насоса и отно­сительной шероховатости поверх­ностей проточной части при условии работы модели в области автомодельности. Наиболее оправдала себя полуэмпирическая формула А. А. Ло­макина:

_г.н=1-(1-_гм)( (9)

где D_пр = (44,5) 10³ — приведенный диаметр входа в рабочее колесо насоса, мм.

Объемные потери и механические потери в подшипниках и сальниках как немоделируемые должны подсчитываться по соответствующим формулам .

При малом отличии n_н от n _м и D_н от D_м, а также при предва­рительных расчетах можно принять в первом приближении равными все значения _н и _м. Благодаря этому формулы пересчета можно представить в более удобном для решения практических задач виде:



(10)



В том случае, когда один и тот же насос, перекачивающий одну и ту же жидкость, испытывается при различных частотах вращения n_н и n _м формулы пересчета еще более упрощаются:
; ; (11)

Коэффициент быстроходности.

Одни и те же значения подачи и напора могут быть получены в насосах с различной частотой вра­щения. Естественно, что конструкция рабочих колес и всех элементов проточной части насоса, равно как и их размеры, при этом меняются. Для сравнения лопастных насосов различных типов пользуются коэф­фициентом быстроходности, объеди­няя группы рабочих колес по прин­ципу их геометрического и кинема­тического подобия.

Коэффициентом быстроходности n_s насоса называется частота враще­ния другого насоса, во всех деталях геометрически подобного рассматри­ваемому, но таких размеров, при которых, работая в том же режиме с напором 1 м, он дает подачу 0,075 м ³ /с.

Численное значение коэффициен­та быстроходности можно определить, воспользовавшись формулами пересчета

Лекция № 5

Тема: Характеристики центробежных насосов: теоретические, рабочие, универсальные, сводные (графики полей). Характеристика трубопровода. Приведенная характеристика насоса. Испытания насосов. Построение рабочих характеристик насоса.

Характеристикой насоса назы­вается графически выраженная зави­симость основных энергетических по­казателей от подачи при постоян­ной частоте вращения вала рабо­чего колеса, вязкости и плотности жидкой среды на входе в насос.

Основные параметры лопастных насосов подача (Q, напор H, мощ­ность N, коэффициент полезного действия  и частота вращения вала рабочего колеса n) находятся в определенной зависимости, которая лучше всего уясняется из рассмот­рения характеристических кривых. Значения напора, мощности и КПД для ряда значений подачи могут быть представлены в виде системы точек в координатах H-Q , N –Q,  -Q. Соединяя точки плавными кривыми, получаем непре­рывную графическую характеристику зависимости рассматриваемых па­раметров от подачи насоса при по­стоянной частоте вращения п. Ос­новной характеристической насоса является график, выражающий зависимость развиваемого насосом напора от подачи H=f(Q) при постоянной частоте вращения п = const. Для построения теорети­ческой характеристики насоса при заданных конструктивных размерах воспользуемся уравнением центро­бежного насоса. Если поток на входе в колесо не закручен, тоН_т= u₂₂ • cos a₂ / g.

Теоретическая подача насоса Q_т = _{об } _z D₂b₂₂sin₂ ,откуда

₂= ,

гдеD₂— диаметр рабочего колеса;

b₂ — ширина рабочего колеса;

Из рис. 1 следует, что

₂ • cos a₂ = u₂ — ₂cos₂

или

₂ • cos a₂ =u₂ —

Подставляя полученное значение ₂ • cos a₂ в основное уравнение теорети­ческого напора, получаем:

Н_т= u₂ ) или

Н_т= (1)

При п = const окружная скорость u₂ будет постоянной. Очевидно, что для

рассматриваемого насоса D₂, b₂ и tg₂ являются постоянными величинами. Обозначая

= А = В



получим: H_r=A—BQ_т. (2)

Таким образом, зависимость тео­ретического напора Н_тот теорети­ческой подачи Q_т выражается урав­нением первой степени, которое в координатах Q _т и Н_тграфически изображается прямыми линиями; наклон этих прямых зависит от зна­чения углового коэффициента, яв­ляющегося функцией угла ₂.

На рис. 1, 2 приведена графи­ческая интерпретация уравнения (2) для различных значений уг­лового коэффициента. Проанализируем положение прямых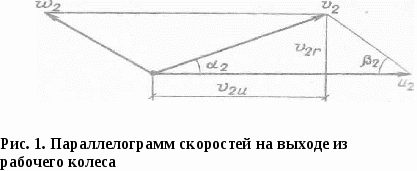




Рис. 2. Теоретическая характеристика

линий при  <9О°,  = 90° и  >90°. Для построения графика зависимости Н-Q предположим, что Q_т =0, тогда Н _т= , а при Н _т =0,

Q_т =_{об } _z D₂b₂₂sin₂ .

При  <9О° (лопатки отогнуты назад) tg ₂ > 0, поэтому с увеличением Q_т напор, развиваемый насосом, Н _т уменьшается. Следовательно, линия зависимости теоретического напора (рис. 2 I) от по дачи направлена наклонно вниз. Наклон прямой I будет тем больше, чем меньше tg_2, т.е. угол _{2 .}

При ₂ = 90° (лопатки направ­лены радиально) tg₂ = , следова­тельно, второй член уравнения (2) будет равен нулю, тогда: Н _т= ,т. е. график зависимости Н_т - Q_т выражается прямой II, параллельной оси абсцисс и отсе­кающей на оси ординат отрезок Н _т= .

При  ₂ >90° (лопатки загнуты вперед) tg ₂ <O, тогда второй член уравнения (2) изменит знак минус на плюс. В этом случае с увеличением подачи возрастает напор причем тем больше, чем больше  ₂ . График зависимости Н_т - Q_т выражается прямой  (см. рис 2.), поднимающейся вверх. При

Q_т=0 начальная ордината прямой  также равна: Н _т = .

Как видно из рис. 2, рабочие колеса с лопатками, загнутыми вперед (прямая ), создают зна­чительно больший напор, чем коле­са с лопатками, загнутыми назад (прямая /), и в этом их основ­ное преимущество. Однако преобра­зование динамического давления, со­здаваемого лопатками, в статиче­ское, путем уменьшения абсолютной скорости потока при выходе из рабочего колеса насоса, связано с большими потерями энергии. Вви­ду этого рабочие колеса центро­бежных насосов, используемых для нагнетания жидкостей, как пра­вило, изготовляются с лопатками, загнутыми назад. Следовательно, для насосов, применяемых в систе­мах водоснабжения и водоотведения, практическое значение имеет лишь одна из этих прямых (линия ) — теоретическая характеристика Н_т - Q_т, соответствующая работе на­соса без учета потерь в нем.

Для получения действительной характеристики насоса необходимо внести поправки на гидравличе­ские потери (в проточной части на­соса), объемные и механические, а также на конечное число лопаток.

Теоретический напор при конеч­ном числе лопаток Н_т^ будет меньше теоретического напора при беско­нечном числе лопаток Н_т. Умень­шение теоретического напора учи­тывается поправочным коэффициен­том на конечное число лопаток k, значение которого меньше 1. Поэ­тому прямая теоретической харак­теристики Н ^_т - Q_т^ (прямая а), учи­тывающая поправку на конечное число лопаток, понизится и отсе­чет на оси Н отрезокН'_т =k _/

Прямая Iи прямая а(см. рис. 2) пересекаются на оси Q , если принять, что коэффициент kне зависит от подачи, или ниже осиQ, если он зависит от подачи. Потери сопротивления протеканию жидкости при турбулентном движении практи­чески можно считать пропорцио­нальными квадрату подачи, т. е. h=SQ².

Таким образом, графиче­ски потери от трения в каналах изображаются квадратичной пара­болой с вершиной в начале коор­динат (см. рис. 2, кривая б).

Откладывая значения этих потерь вниз от линии а, получим кривую б.

Потери на удар при входе жид­кости на лопатки или в направляю­щий аппарат вызываются резким изменением направления средней скорости. Для расчетной подачи Q _р углы наклона лопаток при входе и выходе из колеса или направляю­щего аппарата подбирают таким образом, чтобы не было потерь от удара, т. е. чтобы h _уд = 0. При откло­нении подачи Q_хот расчетной Q_р появляются потери на удар, которые возрастают пропорционально квад­рату отклонения подачи:

h_уд = k'(Q_х -Q_р )².

Графически этому уравнению соответствует параболическая кри­вая с вершиной в точке безудар­ного входа h_уд =0 при Q_х -Q_р (см. рис. 2, кривая в).

В соответствии с уравнением. Бернулли для увеличения статиче­ского (полезного) напора насоса скорость потока у выходного патруб­ка необходимо значительно умень­шить. Из законов гидродинамики жидкости известно, что всякое изме­нение скорости потока сопровождает­ся потерями, прямо пропорциональ­ными квадрату потерянной скорости.

При построении кривой в не принимались в расчет утечки воды через зазоры. Если учитывать эти утечки, то полученные напоры H будут соответствовать меньшим фак­тическим подачам насоса и дей­ствительная характеристика H-Q (кривая г) несколько сместится влево. Так как утечка в совре­менных конструкциях центробежных насосов не превышает 2—5 %, то ее влияние дает незначительное смещение характеристики.

К механическим потерям отно­сятся потери на трение дисков колеса о жидкость и потери трения в подшипниках и сальниках. Эти параметры почти не влияют на характеристику насоса, поэтому мы их здесь не рассматриваем.

Теоретическое построение харак­теристик насосов по заданным раз­мерам встречается с большими труд­ностями. Исследования, проведенные во ВНИИгидромаше, показыва­ют, что строить теоретическую харак­теристику лучше всего комбиниро­ванным способом: по расчетному направлению касательной в точке оптимального значения КПД и по точке холостого хода, полученной сопоставлением относительной ха­рактеристики колеса такой же кон­струкции и с таким же значением коэффициента быстроходности n_s. Однако и в этом случае фактиче­ская характеристика не получается вследствие большого числа факто­ров, которые не поддаются точно­му определению и которыми прихо­дится задаваться. Ввиду этого на практике отдают предпочтение опытным характеристикам, полу­чаемым при испытании насосов.
÷Построение характеристик насосов

Основная трудность в получе­нии характеристик насосов расчет­ным путем заключается в выборе коэффициентов потерь, влияющих на подачу и напор насоса. Поэтому при расчете режима работы насоса поль­зуются опытными характеристиками, которые получают при испытаниях насосов. Насосы, изготовляемые отечественными насосостроительными заводами, подвергаются ис­пытаниям в соответствии с ГОСТ 6134—71. Мелкие и средние насосы испытываются на заводском испы­тательном стенде, крупные насосы допускается испытывать на месте эксплуатации при частоте вращения, отличающейся от номинальной не более чем на 5 %.

На основании опытных измерений подачи и напора на входе и вы­ходе, а также потребляемой мощ­ности и вакуумметрической высоты всасывания, вычисляют напор, приведенный к оси насоса, полезную мощность и

коэффициент полезного действия, допустимого кавитационного запаса для ряда значений подачи (15 -16 точек ) можно представить в виде системы точек в координатах H, N, Q, _h, (рис. 3. а). Соединяя соответствующие точки плавными линиям получаем графики зависимости рассматриваемых параметров от подачи насоса при постоянной частоте вращения для данногодиаметра рабочего колеса.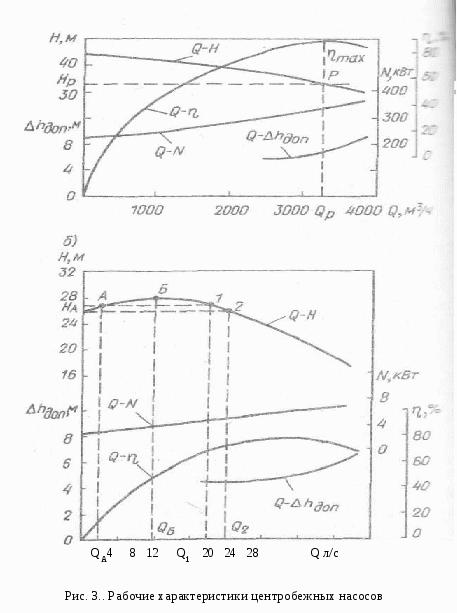



Полученные кривые H- Q, N- Q, - Q, _h - Qназываются энергетическими характеристиками центробежного насоса и вписываются в паспорт насоса. Из рис. 3, а видно, чтоІмаксимальному значению КПД соот­ветствует подача Q_pи напор H_р (расчетные параметры). Точка Р характеристики H- Q, отвечающая максимальному значению КПД, на­зывается оптимальной режимной точкой.

Из теоретической зависимости H- Qследует, что с уменьшением подачи напор возрастает и при по­даче, равной нулю, т. е. при за­крытой задвижке на напорном трубопроводе, достигает максималь­ного значения. Однако испытания показали, что некоторые насосы развивают максимальный напор пос­ле открытия задвижки, т. е. напор возрастает при начальном увеличе­нии подачи, а затем падает. Гра­фическая характеристика (рис. 3, б) имеет восходящую ветвь от Q_o до Q_б. Такие графические ха­рактеристики называются восходя­щими. Из рис. 3, 6 видно, что напору Н_Асоответствуют две по­дачи Q_Aи Q₁. Изменение подачи насоса наступает внезапно, сопро­вождается сильным шумом и гид­равлическими ударами, сила которых зависит от диапазона изменения подачи и длины трубопровода. Ра­бота насоса в пределах подачи от нуля до Q₂ называется областью неустойчивой работы.

Характеристики, не имеющие воз­растающей ветви, называются ста­бильными. Режим работы насосов, имеющих стабильную рабочую ха­рактеристику Н-Q, протекает ус­тойчиво во всех точках кривой. Форма характеристики Н-Qза­висит от коэффициента быстро­ходности насоса n_s, чем больше коэффициент быстро­ходности, тем круче кривая Н-Q .

При стабильной пологой харак­теристике напор насоса даже при значительном изменении подачи из­меняется незначительно. Насосы с пологими характеристиками целе­сообразно применять в системах, где при постоянном напоре тре­буется регулирование подачи в широких пределах, например в безбашенной системе водоснабжения

Е. А. Прегер на основании анали­за характеристик Н-Q составил уравнение, дающее аналитическую зависимость между параметрами Q и Н

H = а₀ +Qa₁+Q² a₂

Ограничиваясь лишь рабочей частью характеристик Н-Q , можно упростить указанное уравнение, а именно:

для насосов чистой воды H = a — bQ²

а для насосов сточных вод H=a — bQ.

Приведенные уравнения справед­ливы в пределах, где рабочие ха­рактеристики Н-Q могут быть при­няты за прямую или квадратич­ную кривую. Коэффициенты а и b постоянны и их значения установ­лены для выпускаемых типоразме­ров насосов.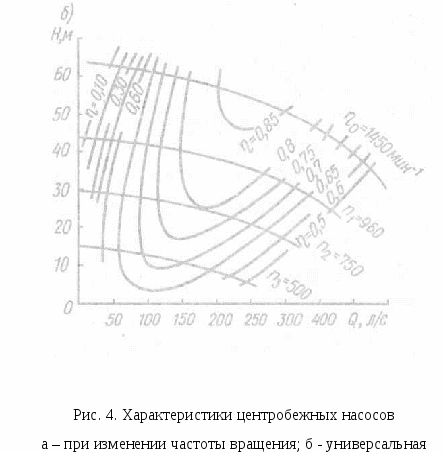

Универсальная характеристика насоса
Универсальная характеристика позволяет наиболее полно исследо­вать работу насоса при переменных частоте вращения, КПД и мощности насоса для любой режимной точки.

Необходимо отметить, что режим работы насоса с пониженной час­тотой вращения допускается, но по­вышение частоты вращения больше чем на 10—15 % должно быть со­гласовано с заводом-изготовителем.

Требования потребителей по по­даче и напору чрезвычайно раз­нообразны и экономически нецеле­сообразно изготовлять насосы для каждого расчетного случая.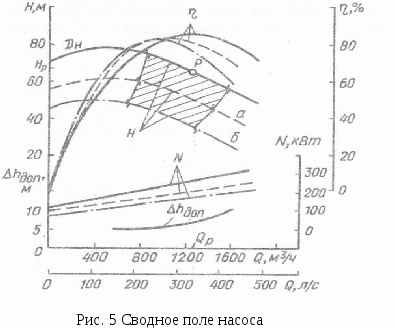





Пространство (на рис. 5 за­штриховано), заключенное между характеристиками Н-Q при номи­нальном размере колеса и Н_cp - Q_cp при максимально допустимой срезке колеса (линия б) и извилистыми линиями, соответствующими по­дачам в пределах рекомендуемых отклонений КПД, называется полем насоса — рекомендуемая область применения насоса.

В каталогах-справочниках при­водятся сводные графики полей насосов. По этим графикам удоб­но подбирать насос на заданный режим работы.

Изменение подачи и напора насоса в рекомендуемой области осуществляется за счет срезки (обточки) рабочего колеса насоса.

Изменение КПД насоса можно рассчитать по формуле Муди, ко­торая применяется в гидротурбо­строении для расчета оптимального значения полного КПД  _н натуры по значению КПД _м модели:

n,_cp=1-(1-)(D/D_cp)^0,25.

Экспериментальное исследование n|_ср показывает, что при срезке коле­са КПД изменяется незначительно в зависимости от коэффициента быстроходности. С достаточной сте­пенью точности можно принять, что КПД насоса уменьшается на 1 % на каждые 10 % срезки колеса с коэффициентом быстроходности n_s = 60÷200 и на 1 % на каждые 4 % срезки при n_s = 200÷300.

В зависимости от коэффициента быстроходности рекомендуются сле­дующие пределы срезки колес:

60 s <120 ...... …………. 20—15%

120 s<200………….……….15—11%

200 s <300 …………………11— 7%
÷Неустановившиеся и переходные режимы работы насосов

В соответствии с уравнением (3) напор насоса НН_макспри Q0. Однако практика эксплуата­ции тихоходных и некоторых нор­мальных насосов, имеющих восходящую характерис­тику, показывает, что напор насоса имеет максимальное значение при Q ≠ 0. При работе насоса в зоне неустойчивой работы (см. рис. 3, б) наблюдается пульсация напора и подачи, т. е. неустановившийся ре­жим работы насоса — помпаж. Помпажный режим работы часто при­водит к возникновению гидравли­ческого удара в сети. Такие насосы обеспечивают устойчивую работу системы при условии H_г<H_о (где H_г — геометрическая высота подъ­ема воды; Н_о— напор насоса при Q = 0).

Рассмотрим совместную работу насоса Д1250-125 (имеющего вос­ходящую характеристику) и водо­водов с характеристикой H_тр.-Q .Пусть характеристикаH_тр.-Q_тр пере­секает характеристику H-Q насоса в двух точках: А на восходящей ветви и Б на падающей ветви (рис. 6). В обеих режимных точках имеются все условия материального и энергетического равновесия сис­темы «насос — водоводы». При уве­личении подачи на величину _Q_А вследствие кратковременного пони­жения требуемого напора в водо­водах H_тр возникает отрицательная разность напоров _H=H_тр –H< 0.

Избыток в системе напора H по сравнению с требуемым H_тр вызывает увеличение кинетической энергии жидкости в системе, ско­рость движения и подача возрас­тают, что ведет к отклонению сис­темы от равновесия в точке А и затем к выпадению системы из равновесия.

Предположим, что система «на­сос — водоводы» работает в режи­ме Б. При увеличении подачи на величину _Q_Б возникает положи­тельная разность напоров: _H=H_тр –H> 0.

Н
едостаток в системе напора H по сравнению с требуемым H_тр может быть компенсирован только за счет кинетической энергии жид­кости в системе. Скорость движения

жидкости при уменьшении Н па­дает, подача уменьшается, в резуль­тате чего достигается равновесие системы.

Следовательно, критерием устой­чивой работы системы является знак разности напора _Н при уве­личении подачи. Математическим критерием устойчивой работы в ре­жимной точке является выполне­ние неравенства

dH_тр /dQ> dH/ dQ.

Неустановившийся режим работы насоса недопустим по соображениям надежности работы всей системы, поэтому при выборе насоса, нужно стремиться к тому, чтобы заданный режим работы насоса лежал в поле рекомендуемой работы насоса.

В настоящее время в СССР уделяется большое внимание раз­работке конструкций насосов с n_s< 100 для получения непрерывно падающих, т. е. стабильных харак­теристик.
÷Характеристика трубопровода

Подача центробежного насоса за­висит от напора и, следовательно, в значительной степени от гидрав­лического сопротивления водоводов и сети движению жидкости, опреде­ляемого их диаметром. Поэтому система «насос — трубопроводы» должна рассматриваться как еди­ная система, а выбор насосного оборудования и трубопроводов должен решаться на основании рас­чета совместной работы составляю­щих элементов системы.

Совместная работа насосов и сети характеризуется точкой мате­риального и энергетического равно­весия системы. Для определения этой точки необходимо вычислить энер­гетические затраты в системе «во­доводы — сеть» Q_p и H_тр. Совмест­ная работа насосов и трубопро­водов связана следующими зави­симостями:

h'=f(Q_p); h₆=G(Q_p,_q); h = j(Q),

где Q— расчетный расход в трубопроводе;

Q_p — подача воды насосом;

q— расход во­ды в системе;

H— напор насоса;

h₆ — уровень воды в баке водонапорной башни;

h — гидравлическое сопротивление водово­дов и сети.

Аналитический расчет режимной точки работы насоса довольно трудо­емкий процесс, так как приходится оперировать четырьмя переменными величинами Q_p , H, q и h, ко­торые находятся между собой в функциональной зависимости.

При расчете системы «насос — водопроводная сеть» используют ме­тод последовательного приближения или производят расчет на электрон­но-вычислительных машинах. Од­нако эти вычисления, не дают на­глядности, и анализ работы насоса весьма затруднен. В практике гид­равлического расчета насосных стан­ций и при анализе режимов работы насосов широко применяется метод графо-аналитического расчета сов­местной работы системы «насосы - сеть».

Насосы в системе работают в соответствии с характерной для них зависимостью между Qи H, т. е. график работы насоса определяется его характеристикой Н-Q.

Для построения графической характеристики - системы подачи и распределения воды воспользуемся известными уравнениями гидравлики.­

Требуемый напор в системе равен сумме геометрической высоты подъема жидкости и потерь напора:

H_тр = H_г + h_вс+h_н =H_г+h (3)

где H_г — геометрическая высота подъема жидкости;

h_вс — потери напора во вса­сывающем трубопроводе и коммуникациях насосной станции;

h_н — то же, в напорных водоводах от насосной станции до точки присоеди­нения к сети и в напорных коммуникациях насосной стан­ции;,

Потери напора в трубопроводах складываются из потерь на преодо­ление трения при движении жидкос­ти по трубопроводу h_l и потерь на преодоление сопротивлений в его фасонных частях (местных сопротив­лений) h_м, т. е.

h_вс = h_l + h_м (4)

Гидравлические потери по длине трубопровода могут быть определены по формуле

h_l=илиh_l = k ,

где l - длина трубопровода, м;

D - расчетный внутренний диаметр трубы, м;

 - средняя скорость движения воды, м/с;

Q — подача, м³/с;

g - ускорение свобод­ного падения, м/с²;

k- коэффициенты потерь напора.

Для определения потерь напора в трубопроводе при построении его ха­рактеристики Q— Н удобно восполь­зоваться формулой

h = SQ² = S_всQ2+ S_нQ² , (5)

где S=S_оl -сопротивление трубопровода;

S_о - удельное сопротивление;

S_вс , S_н – удельное сопротивление во всасывающей и напорной линии.

Потери напора на местные сопротивления по длине трубопровода принимаются в пределах 1020%, в пределах насосной станции 0,55 м.

Исследования Ф. А. Шевелева показали, что пропорциональность сопротивлений квадрату подачи при движении воды по трубам со ско­ростью менее 1,2 м/с нарушается и в значение удельных сопротивлений необходимо вводить поправку .

Диаметры труб, фасонных частей и арматуры следует принимать на основании технико-экономическо­го расчета, исходя из скоростей в пределах, указанных в СНиП.

Приведенная характеристика насоса

Из формулы (5) следует, что напор в точке выхода жидкости из насоса равен напору, развивае­мому насосом и уменьшенному на величину потерь во всасывающем трубопроводе.

Графическая характеристика на­соса Н-Q (рис. 7), построен­ная с учетом потерь во всасываю­щем трубопроводе, называется при­веденной характеристикой.

Для построения графической характерис­тики всасывающего трубопровода воспользуемся уравнением (5). При заданном расчетном расходе Q_p определим h_вс, которые можно выразить как функцию подачи:

h_{ вс} = S_всQ² (6)

Задаваясь подачей Q_x, получим характеристику всасывающего трубопровода h_{ вс}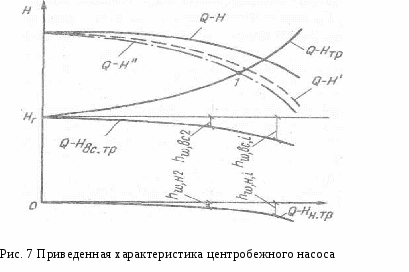


В координатной сетке Н- Q от линии Н_г отложим ординаты h_{ вс 1,} h_{ вс 2} ,h_{ вс i} для соответствую­щих подач Q_i, Q₂, Q_i. Соединяя точки плавной кривой, получим па­раболическую кривую, т. е. графи­ческую характеристику h_{ вс} всасывающего трубопровода (см. рис.7). Вычитая ординаты кри­вой h_{ вс} из ординат кривой Н- Qнасоса и соединяя найден­ные точки плавной кривой, полу­чим характеристику Н- Q' насо­са, приведенную к точке входа жид­кости в насос и исправленную на потери во всасывающем трубопро­воде.

Подобные расчеты можно произ­вести и для напорных коммуни­каций насосной станции. Введя поправку h_{ н} в приведенную ха­рактеристику Н- Q' на потери в напорных коммуникациях, получим характеристику Н- Q", приведенную к точке выхода напорных водо­водов с насосной станции.

Аналогично можно построить графическую характеристику системы «водоводы – сеть».

Лекция № 6