Лекции по гидравлике. Лекция введение. Предмет гидравлики и краткая история ее развития рис. Разделы гидромеханики
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
|
Лекция 1. ВВЕДЕНИЕ. ПРЕДМЕТ ГИДРАВЛИКИ И КРАТКАЯ ИСТОРИЯ ЕЕ РАЗВИТИЯ  Рис. 1.1. Разделы гидромеханики Гидравлика (техническая механика жидкости) - прикладная часть гидромеханики, которая использует те или иные допущения для решения практических задач. Она обладает сравнительно простыми методиками расчета по сравнению с теоретической механикой жидкости, где применяется сложный математический аппарат. Однако гидравлика дает достаточную для технических приложений характеристику рассматриваемых явлений. 1.2. Жидкость и силы, действующие на неё Жидкостью в гидравлике называют физическое тело способное изменять свою форму при воздействии на нее сколь угодно малых сил. Различают два вида жидкостей: жидкости капельные и жидкости газообразные (рис.1.2).  Рис. 1.2. Виды жидкостей  Рис. 1.3. Сжатие жидкостей и газов
где F - сила, действующая на жидкость, Н (ньютоны); S - площадь, на которую действует эта сила, м² (кв.метры). 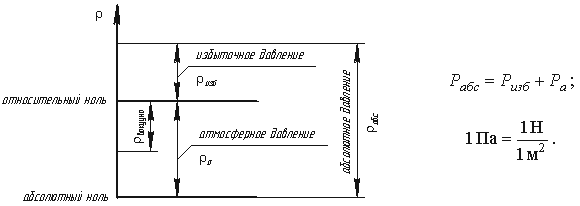 Рис. 1.5. Схема к определению давлений За единицу давления в Международной системе единиц (СИ) принят паскаль - давление вызываемое силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м²: 1 Па = 1 Н/м² = 10-3 кПа = 10-6 МПа. Размерность давления обозначается как "Па" (паскаль), "кПа" (килопаскаль), "МПа" (мегапаскаль). В технике в настоящее время продолжают применять систему единиц МКГСС, в которой за единицу давления принимается 1 кгс/м². 1 Па = 0,102 кгс/м² или 1 кгс/м² = 9,81 Па. 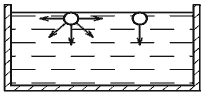 Рис. 1.6. Силы поверхностного натяжения 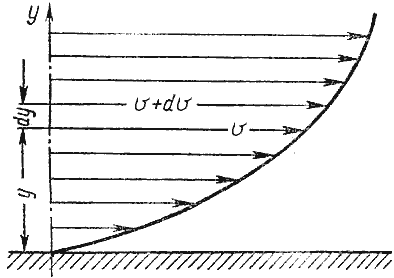 Рис. 1.7. Профиль скоростей при течении вязкой жидкости вдоль стенки 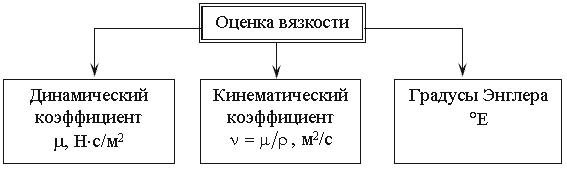 Рис. 1.8. Способы оценки вязкости жидкости Лекция 2. ОСНОВЫ ГИДРОСТАТИКИ Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение. 2.1. Гидростатическое давление В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Если эту силу P разделить на площадь дна Sabcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара. Гидростатическое давление обладает свойствами. Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости. 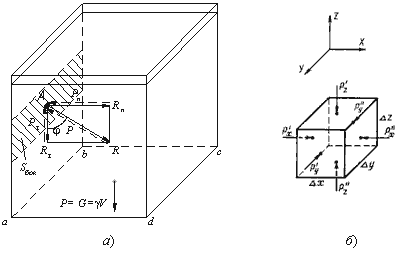 Рис. 2.1. Схема, иллюстрирующая свойства гидростатического давления: а - первое свойство; б - второе свойство Свойство 2. Гидростатическое давление неизменно во всех направлениях. Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве. 2.2. Основное уравнение гидростатики 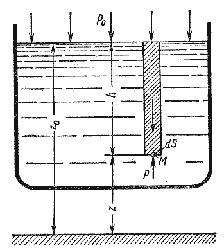 Рис. 2.2. Схема для вывода основного уравнения гидростатики 2.3. Давление жидкости на плоскую наклонную стенку 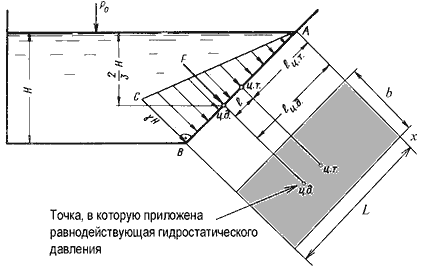 Рис. 2.3. Схема к определению равнодействующей гидростатического давления на плоскую поверхность 2.4. Давление жидкости на цилиндрическую поверхность 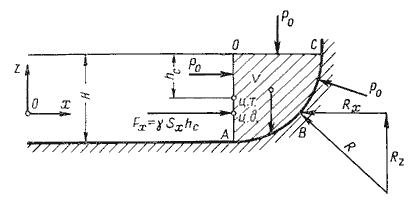 Рис. 2.4. Схема к определению равнодействующей гидростатического давления на цилиндрическую поверхность 2.5. Закон Архимеда и его приложение 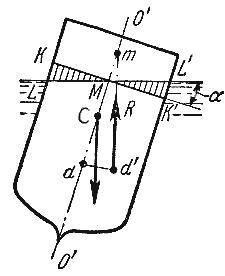 Рис. 2.5. Поперечный профиль судна Лекция 3. ОСНОВЫ ГИДРОДИНАМИКИ Гидродинамика - раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями. 3.1. Основные понятия о движении жидкости Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. 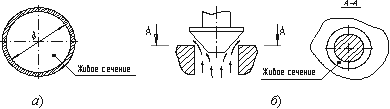 Рис. 3.1. Живые сечения: а - трубы, б - клапана Смоченный периметр χ ("хи") - часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией). 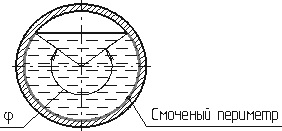 Рис. 3.2. Смоченный периметр Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω: Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной. Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.  Рис. 3.3. Линия тока и струйка 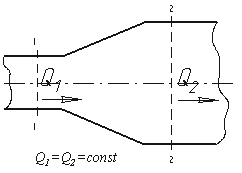 Рис. 3.4. Труба с переменным диаметром при постоянном расходе Уравнение Бернулли для идеальной жидкости 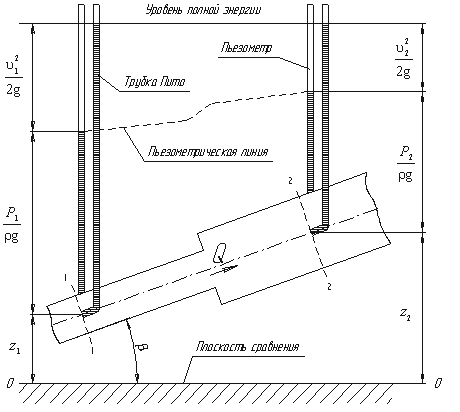 Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости Уравнение Бернулли для реальной жидкости 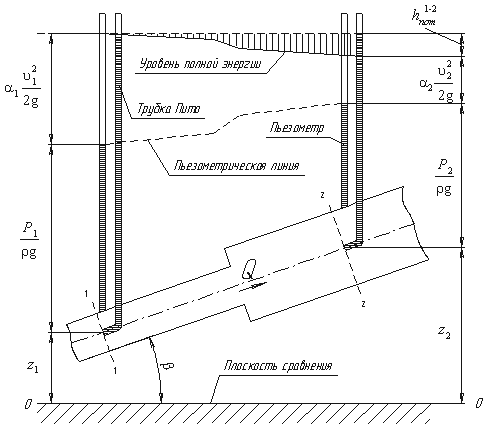 Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости Уравнение Бернулли для реальной жидкости будет иметь вид: Измерение скорости потока и расхода жидкости 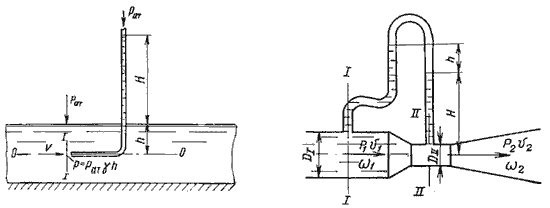 Рис. 3.7. Трубка Пито и pасходомер Вентури Лекция 4. ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ 4.1. Режимы движения жидкости 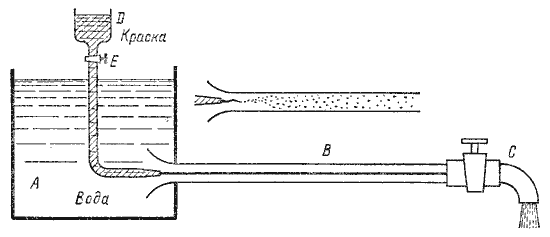 Рис. 4.1. Схема установки Рейнольдса где ν - кинематическая вязкость; k - безразмерный коэффициент; d - внутренний диаметр трубы. 4.2. Кавитация 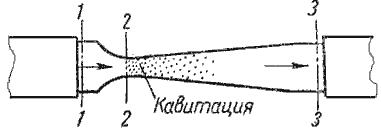 Рис. 4.2. Схема трубки для демонстрации кавитации 4.3. Потери напора при ламинарном течении жидкости 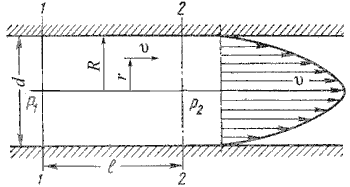 Рис. 4.3. Схема для рассмотрения ламинарного потока где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению: Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re < 2300 применять формулу 4.4. Потери напора при турбулентном течении жидкости Х 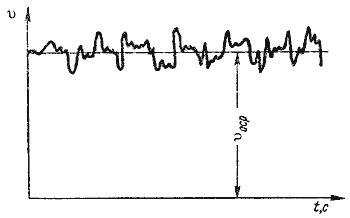 арактер линий тока в трубе в данный момент времени отличается большим разнообразием (рис.4.5). Рис. 4.4. Пульсация скорости в турбулентном потоке Р  ис. 4.5. Характер линий тока в турбулентном потоке Р 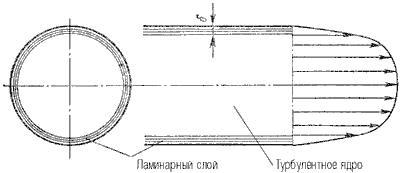 ис. 4.6. Модель турбулентного режима движения жидкости формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид: 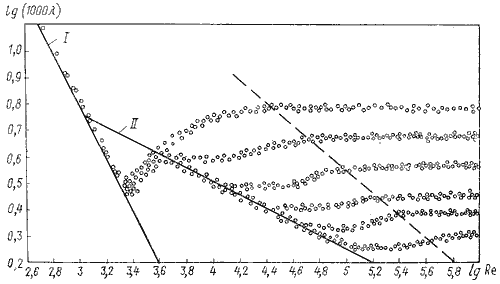 Рис. 4.7. График Никурадзе
Таблица 4.1 Таблица для определения коэффициента гидравлического трения 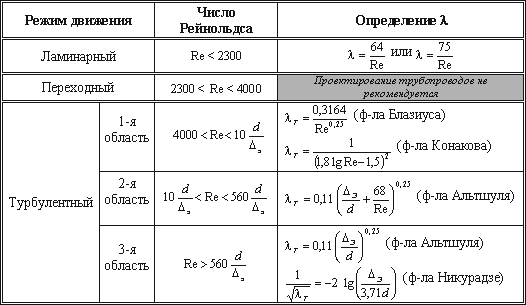 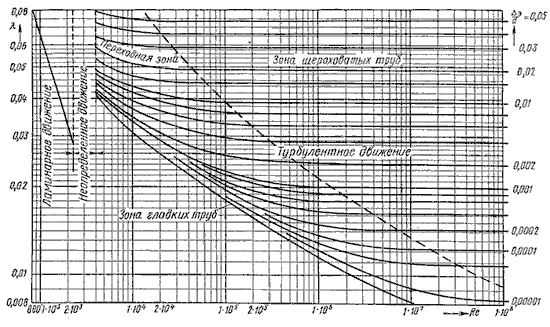 Рис. 4.8. Номограмма Колбрука-Уайта для определения коэффициента гидравлического трения 4.5. Местные гидравлические сопротивления 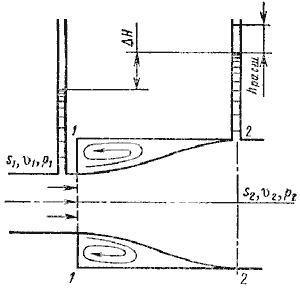 Рис. 4.9. Внезапное расширение трубы где S1, S2 - площадь поперечных сечений 1-1 и 2-2. 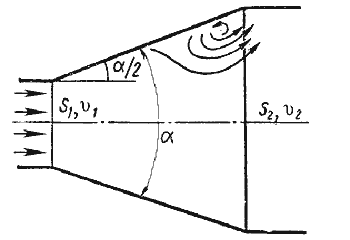 Рис. 4.10. Постепенное расширение трубы 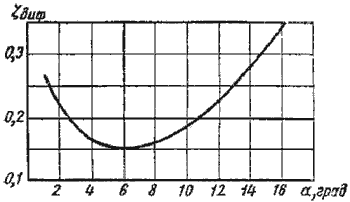 Рис. 4.11. Зависимость ζдиф от угла 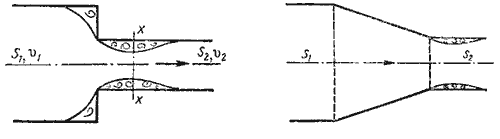
Полная потеря напора определится по формуле ;  Рис. 4.14. Сопло 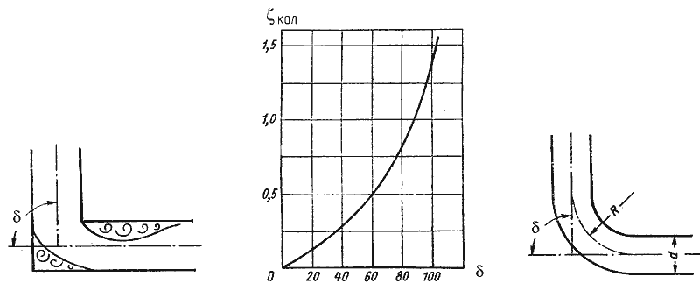
Лекция 5. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, НАСАДКОВ И ИЗ-ПОД ЗАТВОРОВ 5.1. Истечение через малые отверстия в тонкой стенке при постоянном напоре 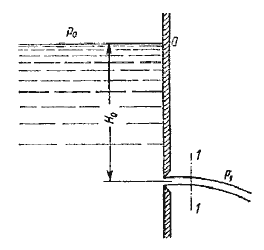 Рис. 5.1. Истечение из резервуара через малое отверстие 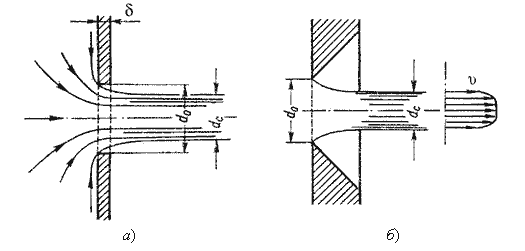 Рис. 5.2. Истечение через круглое отверстие 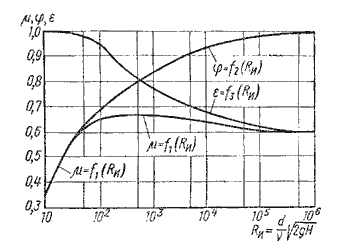 
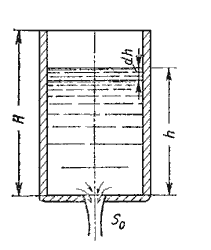
5.2. Истечение при несовершенном сжатии Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5). 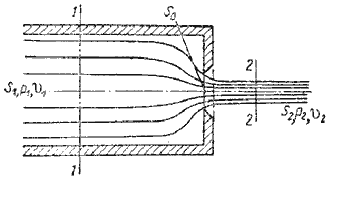 Рис. 5.5. Схема несовершенного сжатия струи 5.3. Истечение под уровень 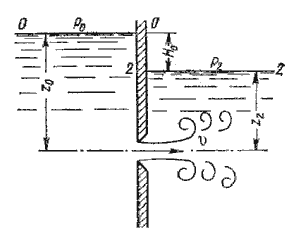 Рис. 5.6. Истечение по уровень 5.4. Истечение через насадки при постоянном напоре 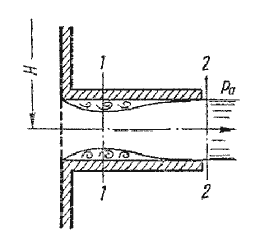 Рис. 5.7. Истечение через насадок Коэффициент расхода μ, зависящий от относительной длины насадка l / d и числа Рейнольдса, определяется по эмпирической формуле: 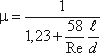 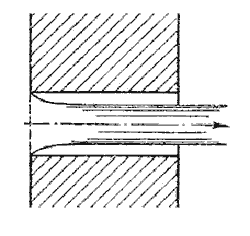 Рис. 5.8. Второй режим истечения через насадок  Рис. 5.9. Истечение жидкости через насадки а - расширяющиеся конические; б - сужающиеся конические; в - коноидальные; г - внутренние цилиндрические 5.5. Истечения через отверстия и насадки при переменном напоре (опорожнение сосудов) 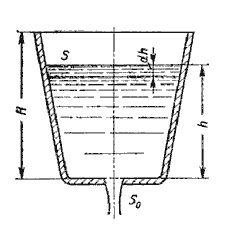 Рис. 5.10. Схема опорожнения резервуара
5.6. Истечение из-под затвора в горизонтальном лотке 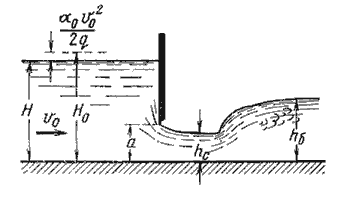 Рис. 5.13. Истечение из-под затвора через незатопленное отверстие 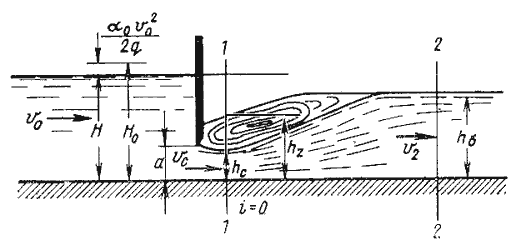 Рис. 5.14. Истечение из-под затвора при затопленном отверстии 5.7. Давление струи жидкости на ограждающие поверхности 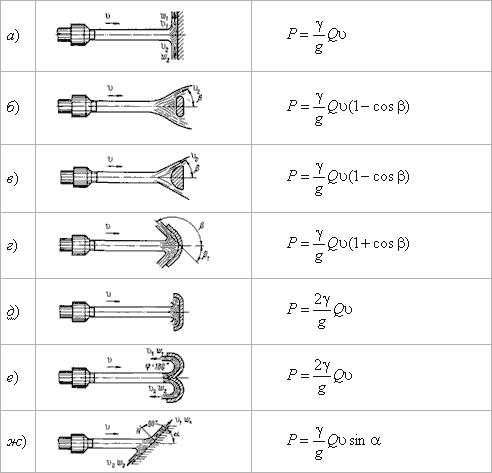 Рис. 5.15. Взаимодействие струи жидкости с неподвижной поверхностью 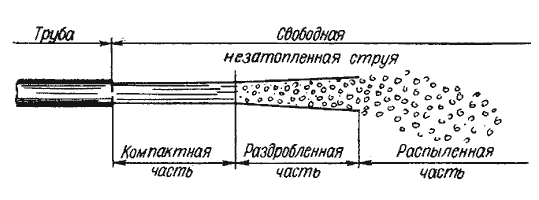 Рис. 5.16. Составные части свободной струи Лекция 6. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ПРОСТЫХ ТРУБОПРОВОДОВ 6.1. Простой трубопровод постоянного сечения 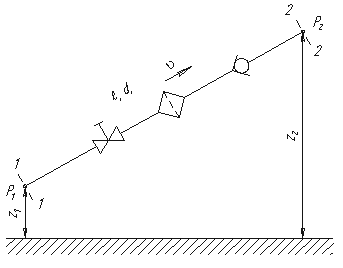 Рис. 6.1. Схема простого трубопровода 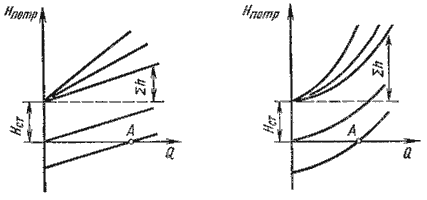 Рис.6.2. Зависимости потребных напоров от расхода жидкости в трубопроводе |