лекции по биостатистике+. Лекциях по направлению подготовки Ветеринария

• Название: Лекциях по направлению подготовки Ветеринария
• Дата: 02.06.2022
• Размер: 355.81 Kb.
• Имя файла: лекции по биостатистике+.docx
• Тип: Лекция; #564504
• страница: 8 из 8

7.Оценка параметров генеральной совокупности

Характеристики положения

Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение . Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.

Точечной оценкой генеральной средней является выборочное среднее  .

Выборочным средним называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, x₂,..., x_n признака выборки различны (или если данные не сгруппированы), то: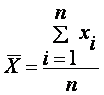



Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁ + n₂ +...+ n_k = n (или если выборочное среднее вычисляется по вариационному ряду), то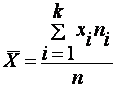



В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего   значениями вариант считают середины интервалов.

Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0).

Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.

Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году.

Выборочной дисперсией D_в называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  .

Если все значения x₁, x₂,..., x_n признака выборки объема n различны, то: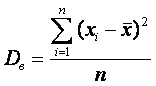



Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁ + n₂ +...+ n_k = n, то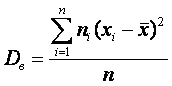



Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.

Среднее квадратическое отклонение (стандартное отклонение), (от английского standard deviation) вычисляется как корень квадратный из дисперсии.



Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.

Непараметрическими характеристиками положения являются мода и медиана.

Модой M_o называется варианта, имеющая наибольшую частоту или относительную частоту.

Медианой M_e называется варианта, которая делит вариационный ряд на две части, равные по числу вариант.

При нечетном числе вариант (n=2k+1)

M_e = x_k+1,

а при четном числе вариант (n=2k)

M_e = (x_k + x_k+1)/2.
8. Проверка статистических гипотез
8.1. Метод последовательного анализа
Пусть в результате проведения серии из независимых испытаний для случайной величины получен статистический ряд её значений , После обработки опытных данных находят статистическую функцию распределения, вычисляют оценки параметров и выдвигают гипотезу относительно закона распределения случайной величины . Для проверки принятой гипотезы (третья задача математической статистики) существует несколько математических методов. Одним из таких методов является метод последовательного анализа, сущность которого состоит в следующем:

– выбирают критерий проверки (например, саму случайную величину , значения которой зависят от номера проведенного опыта);

– назначают точность эксперимента и надежность получаемых результатов;

– проводят испытания и определяют значение критерия проверки;

– если критерий проверки соответствует принятой гипотезе , то она принимается, в противном случае – отвергается.

Если по методу последовательного анализа построить зависимость, например, случайной величины от номера проводимого опыта, то получим три области, размеры которых определяются точностью эксперимента и уровнем надежности получаемых результатов в зависимости от принятой гипотезы о законе распределения случайной величины

Если график зависимости входит в область I при числе опытов , то гипотеза заменяется новой гипотезой (траектория (1)), и опыты повторяются. Если график зависимости находится в области II, то испытания продолжаются до тех пор, пока гипотеза будет либо отброшена, либо принята (траектория (2)). Если график зависимости входит в область III при числе опытов , то гипотеза принимается, и опыты прекращаются (траектория. Для реализации метода последовательного анализа разработано несколько математических способов, из которых рассмотрим способ Пирсона (критерий ) и способ академика А.Н. Колмогорова.

..

8.2. Способ Пирсона (критерий )

В способе Пирсона в качестве критерия проверки используется величина , где – число интервалов, на которые разбивается вся выборка, – число проведенных испытаний, – теоретическая вероятность того, что случайная величина попадает в интервал , а – относи-тельная частота попадания этой случайной величины в тот же интервал. При увеличении числа опытов случайная величина практически не зависит от числа испытаний и её закон распределения приближается к закону распределения “хи-квадрат ()”. Теоретические вероятности вычисляются в соответствии с принятой гипотезой о законе распределения случайной величины и оценкам её параметров распределения. Вычисляя число “степеней свободы”, задавая уровень значимости (обычно принимают ), по таблицам для распределения “хи-квадрат ” находят . Если , то гипотеза принимается, в противном случае – отвергается.

Достоинством способа Пирсона является то, что он применим тогда, когда известен вид гипотетического распределения, но неизвестны его параметры. К недостаткам этого способа относятся:

– его применимость при числе опытов ; 100.n

– количество интервалов и частота попадания в интервал ;

– результаты проверки зависят от способа разбиения выборки на интервалы.

8.3. Способ А.Н. Колмогорова

В этом способе в качестве критерия проверки выбирается случайная величина , который представляет собой наибольшее значение разности между значениями теоретической и статистической функциями распределения. Академик А.Н. Колмогоров доказал, что независимо от вида закона распределения случайной величины при существует предел вероятности того, что величина , где – некоторое число. При достаточно большом числе опытов () выполняется приближенное равенство . Отсюда следует схема применения способа А.Н. Колмогорова:

– вычисляют модуль наибольшей разности между теоретической и статистической функциями распределения и критерий проверки ;

– назначают уровень значимости (принимают );

– по соответствующим таблицам находят критическое значение величины

из равенства ;

.– если расчетное значение критерия проверки , то гипотеза отбрасывается, в противном случае – принимается.

Достоинством способа А.Н. Колмогорова состоит в том, что он не требует сложных расчетов. К недостаткам этого способа относятся:

– для применения этого способа надо знать не только вид закона распределения, но и его параметры;

– критерий проверки учитывает только модуль наибольшей разности между теоретической и статистической функциями распределения, но не закон изменения этого отклонения по всему объему выборки.

Контрольные вопросы
1. Что такое генеральная совокупность? Выборочная совокупность? Объем выборки?

2. Дайте определение понятию вариационный ряд. Что такое статистическое распределение выборки?

3. Что такое полигон и гистограмма частот?

4. Как определяются точечные и интервальные оценки параметров распределения?

5. В чем заключается метод последовательного анализа при проверке статистической гипотезы? Какие еще методы существуют?
Примеры тестовых заданий

Как называется численное значение признака?

• 
  . объемом выборки;
  
• 
  . генеральной совокупностью;
  
• 
  . вариантой;
  
• 
  . средним значением
  

Выборка это
. ограниченное число выбранных случайным образом произвольных элементов;

• 
  . ограниченное число элементов, выбранных неслучайно;
  
• 
  . большая совокупность элементов, для которой оцениваются характеристики.
  
• 
  . ограниченная часть объектов, наиболее полно характеризующая свойства генеральной совокупности
  

Статистическим распределением называется

• 
  . перечень вариант;
  
• 
  . перечень вариант или интервалов и соответствующих частот;
  
• 
  . перечень вариант или интервалов и соответствующих вероятностей;
  
• 
  . перечень значений случайной величины или ее интервалов и соответствующих вероятностей.
  

Оценкой параметра называется

• 
  . приближенное случайное значение параметра генеральной совокупности, которое определяется по всем данным генеральной совокупности;
  
• 
  . приближенное случайное значение параметра генеральной совокупности, которое определяется по данным выборки;
  
• 
  . приближенное неслучайное значение параметра генеральной совокупности, которое определяется по данным выборки.
  
• 
  . приближенное неслучайное значение параметра генеральной совокупности, которое определяется по данным генеральной совокупности.
  

Среднее значение выборки является

• 
  . несмещенной оценкой математического ожидания;
  
• 
  . смещенной оценкой математического ожидания;
  
• 
  . смещенной оценкой дисперсии;
  
• 
  . несмещенной оценкой дисперсии.
  

Литература
1. Кудинов Ю. И. Основы современной информатики : учеб. пособие для вузов

/Кудинов Ю. И., Пащенко Ф. Ф. - СПб. :Лань, 2018. - 256 с.

2. Макарова Н.В., Волков В.Б. Информатика: Учебник для вузов. – СПб.: Пи-

тер, 2017. – 576.

3. Могилев А. В. Информатика : учеб. пособие для вузов /Могилев А. В. , Пак

Н. И., Хеннер Е. К. - М. :Академия, 2018. - 848 с. - (Высшее профессиональ-

ное образование)

4. Новожилов О. П. Информатика : учеб. пособие для бакалавров /Новожилов

О. П., - М. :Юрайт, 2017. - 564 с.

5. Симонович С.В. Информатика. Базовый курс : учеб. для вузов. 3-е изд.

Стандарт третьего поколения. - СПб. :Питер, 2017. - 640 с.

6. Степанов А. Н. Информатика. Базовый курс : учеб. пособие для вузов

/Степанов А. Н., - СПб. :Питер, 2018. - 720 с.