лекции по биостатистике+. Лекциях по направлению подготовки Ветеринария

• Название: Лекциях по направлению подготовки Ветеринария
• Дата: 02.06.2022
• Размер: 355.81 Kb.
• Имя файла: лекции по биостатистике+.docx
• Тип: Лекция; #564504
• страница: 6 из 8

Тема: ОСНОВЫ МАТЕМАТИЧЕСКОЙ БИОСТАТИСТИКИ, ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ

1. 
   Предмет и основные понятия теории вероятностей
   
2. 
   Способы определения вероятностей событий
   
3. 
   Элементы комбинаторики
   
4. 
   Арифметика случайных событий
   
5. 
   Понятие случайной величины. Виды событий. Вероятность события Функция распределения
   

Продолжительность - 4 часа
1. Предмет теории вероятностей
Теория вероятностей – это математическая дисциплина, которая устанавливает взаимозависимость между случайными величинами в случайных массовых процессах. Одним из основных понятий в теории вероятностей является понятие случайного события.

1. Случайным событием называется факт, который в результате проведения эксперимента может произойти или не произойти.

Например, при подбрасывании монеты нельзя угадать заранее, что выпадет: “решка” (аверс) или “орел” (реверс). Каждое из этих событий является простым и не может быть выражено через более простые события.

2. Элементарным событием называется факт, который в результате проведения эксперимента может произойти или не произойти, и не может быть представлено посредством более простых событий.

В теории вероятностей случайные элементарные события принято обозначать заглавными начальными буквами латинского алфавита A, B , C, D, … Элементарные события образуют более сложные события, которые выражаются посредством этих событий. В обоих определениях случайных событий присутствует понятие “эксперимент” (“опыт”).

3. Сложным случайным событием называется событие, которое состоит из осуществления двух или более элементарных событий.

4. Эксперимент – это создание заранее заданного комплекса условий.

Например, при подбрасывании монеты создают следующие условия: стол, на который падает монета, должен быть ровным, гладким, достаточно большим по площади, чтобы монета не могла скатиться.

5. Достоверным событием называется такой факт, который обязательно произойдет в рамках данного опыта.

Достоверное событие обозначается .p .

6. Невозможным событием называется такой факт, который ни при каких условиях не может произойти.

Например, совокупность выигрыша, проигрыша и ничья в шахматной партии образуют достоверное совокупное событие, т.е. одно из этих событий обязательно произойдет при игре в шахматы. При бросании кубика выпадение грани с 7 очками является невозможным событием.

7. Совместными событиями называются события, которые могут одновременно произойти в рамках данного опыта, все другие события называются несовместными.

Например, при бросании кубика выпадение грани с 4 очками (событие ) и выпадение четной грани (событие ) являются совместными событиями, а выпадение грани с 3 очками (событие ) и выпадение четной грани (событие) являются несовместными событиями.

8. Полной группой случайных событий называется совокупность таких несовместных событий, что в результате проведения эксперимента хотя бы одно из них обязательно произойдет.

9. Противоположными событиями называются такие несовместные события, которые образуют полную группу

Например, если событие состоит в попадании снаряда в цель, то событие состоит в том, что снаряд не попадет в цель.

10. Если в словесном описании случайного события присутствуют слова “хотя бы один”, то такое событие противоположно событию, содержащему в своем словесном описании слова “ни один”.

11. Равновозможными событиями называются такие случайные события, которые в условиях данного опыта имеют объективно равные шансы произойти или не произойти.

Например, однородность материала кости и несмещенность центра тяжести кубика являются теми условиями, при которых объективно возможно выпадение любой грани кубика.

2. Способы определения вероятности событий.

2.1. Классическое определение вероятности.
1. Вероятность события – это численная мера степени объективной возможности события. Классическое определение вероятности применяется для нахождения вероятности конечного числа несовместных и равновозможных событий, образующих полную группу.

Пример 1. Пусть в урне находится 6 шаров: 1 белый, 2 красных и 3 синих. Опыт состоит в том, что из урны наудачу извлекают один шар. Определить полную группу случайных событий и наиболее вероятное событие.

Для данного опыта полная группа событий состоит из 6 равновозможных исходов. Обозначим через событие, состоящее в том, что из урны извлекают белый шар; – красный шар; – синий шар. Очевидно, событие является более объективно возможным событием, чем события и , так как синих шаров в урне больше, чем белых и красных.

Классическое определение вероятности состоит в следующем:

2. Вероятностью случайного элементарного события называется отношение числа элементарных исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных, несовместных, элементарных исходов, образующих полную группу.

3. Число, являющееся выражением меры объективной возможности наступления события, называется вероятностью этого события и обозначается символом Р(А).

Определение. Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.  .

Следовательно, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, подсчитать все возможные несовместные исходы n, выбрать число интересующих нас исходов m и вычислить отношение m к n.

Из этого определения вытекают следующие свойства:

Вероятность любого испытания есть неотрицательное число, не превосходящее единицы.

Действительно, число m искомых событий заключено в пределах  . Разделив обе части на n, получим

.

2. Вероятность достоверного события равна единице, т.к.  .

3. Вероятность невозможного события равна нулю, поскольку  .

Задача 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?

Решение. Общее число различных исходов есть n=1000. Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле, получим

.

Задача 2. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.

Решение. Число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5 т.е.



Подсчитаем число m, благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:

.

Число способов выборки трех качественных деталей из 14 имеющихся качественных равно

.

Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций m составляет

.

Искомая вероятность события А равна отношению числа исходов m, благоприятствующих этому событию, к числу n всех равновозможных независимых исходов:

.

3. Элементы комбинаторики

В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3,: , 9 и составлять из них комбинации, то будем получать различные числа, например 143, 431, 5671, 1207, 43 и т.п.

Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 143 и 431), другие - входящими в них цифрами (например, 5671 и 1207), третьи различаются и числом цифр (например, 143 и 43).

Таким образом, полученные комбинации удовлетворяют различным условиям.

В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

Предварительно познакомимся с понятием факториала.

Произведение всех натуральных чисел от 1 до n включительно называют n-факториаломи пишут  .

Пример.

Вычислить: а)  ; б)  ; в)  .

Решение. а)  .

б) Так как   и  , то можно вынести за скобки 

Тогда получим

.

в)  .

Перестановки

Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.

Перестановки обозначаются символом Р_n, где n- число элементов, входящих в каждую перестановку. (Р - первая буква французского слова permutation- перестановка).

Число перестановок можно вычислить по формуле



или с помощью факториала:



Запомним, что 0!=1 и 1!=1.

Пример. Сколькими способами можно расставлять на одной полке шесть различных книг?

Решение. Искомое число способов равно числу перестановок из 6 элементов, т.е.

.

Размещения

Размещениями из m элементов в n в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком из расположения.

Размещения обозначаются символом  , где m- число всех имеющихся элементов, n- число элементов в каждой комбинации. (А-первая буква французского слова arrangement, что означает "размещение, приведение в порядок").

При этом полагают, что n m.

Число размещений можно вычислить по формуле

,

т.е. число всех возможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m.

Запишем эту формулу в факториальной форме:

.

Пример. Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов?

Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.

.

Сочетания

Сочетаниями называются все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом (здесь m и n-натуральные числа, причем n   m).

Число сочетаний из m элементов по n обозначаются   (С-первая буква французского словаcombination - сочетание).

В общем случае число из m элементов по n равно числу размещений из m элементов по n, деленному на число перестановок из n элементов:



Используя для чисел размещений и перестановок факториальные формулы, получим:



Пример. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Решение. Так как порядок выбранных четырех человек не имеет значения, то это можно сделать  способами.

Находим по первой формуле

.

Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:

 

(по определению полагают   и  );

.

Решение комбинаторных задач

Задача 1. На факультете изучается 16 предметов. На понедельник нужно в расписание поставить 3 предмета. Сколькими способами можно это сделать?

Решение. Способов постановки в расписание трех предметов из 16 столько, сколько можно составить размещений из 16 элементов по 3.

.

Задача 2. Из 15 объектов нужно отобрать 10 объектов. Сколькими способами это можно сделать?

Решение.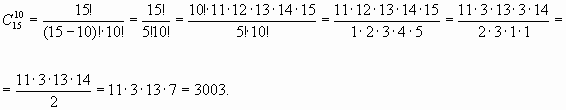



Задача 3. В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно?

Решение.

.

Задача 4. Сколькими способами можно составить дозор из трех солдат и одного офицера, если имеется 80 солдат и 3 офицера?

Решение. Солдат в дозор можно выбрать



способами, а офицеров   способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется   способов.

Задача 5. Найти  , если известно, что  .

Решение.

Так как  , то получим

,

,

,



,  .

По определению сочетания следует, что  ,  . Т.о.  .

Ответ: 9

4. Арифметика случайных событий

Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них.

Сумму двух событий обозначают символом А+В, а сумму n событий символом А₁+А₂+ : +А_n.

Теорема сложения вероятностей.

Вероятность суммы двух несовместных событий равна  сумме   вероятностей этих событий.

 или



Следствие 1. Если событие А₁, А₂, : ,А_n образуют полную систему, то сумма вероятностей этих событий равна единице.

.

Следствие 2. Сумма вероятностей противоположных событий   и   равна единице.

.

Задача 1. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб, на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.

Решение. Пусть А, В, и С- события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20000, 15000 и 10000 руб. так как события А, В и С несовместны, то

.

Задача 2. На заочное отделение техникума поступают контрольные работы по математике из городов А, В и С. Вероятность поступления контрольной работы из города А равна 0,6, из города В - 0,1. Найти вероятность того, что очередная контрольная работа поступит из города С.

Решение. События "контрольная работа поступила из города А", "контрольная работа поступила из города В" и "контрольная работа поступила из города С" образуют полную систему, поэтому сумма их вероятностей равна единице:

, т.е.  .

Задача 3. Вероятность того, что день будет ясным,  . Найти вероятность   того, что день будет облачным.

Решение. События "день ясный" и "день облачный" противоположные, поэтому

, т.е  .

Теорема умножения вероятностей независимых событий

При совместном рассмотрении двух случайных событий А и В возникает вопрос:

Как связаны события А и В друг с другом, как наступление одного из них влияет на возможность наступления другого?

Простейшим примером связи между двумя событиями служит причинная связь, когда наступление одного из событий обязательно приводит к наступлению другого, или наоборот, когда наступление одного исключает возможность наступления другого.

Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

Определение. Пусть А и В - два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что наступило событие В, называется число  .

Обозначив условную вероятность  , получим формулу

,  .

Задача 1. Вычислить вероятность того, что в семье, где есть один ребенок- мальчик, родится второй мальчик.

Решение. Пусть событие А состоит в том, что в семье два мальчика, а событие В - что один мальчик.

Рассмотрим все возможные исходы: мальчик и мальчик; мальчик и девочка; девочка и мальчик; девочка и девочка.

Тогда  ,   и по формуле находим

.

Событие А называется независимым от события В, если наступление события В не оказывает никакого влияния на вероятность наступления события А.

Теорема умножения вероятностей

Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий:

.

Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле

.

Задача 2. В первой урне находится 6 черных и 4 белых шара, во второй- 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми.

Решение. Пусть   - из первой урны извлечен белый шар;  - из второй урны извлечен белый шар. Очевидно, что события   и   независимы.

Так как  ,  , то по формуле   находим

.

Задача 3. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) оба элемента будут работать.

Решение. Пусть событие А- выход из строя первого элемента, событие В- выход их строя второго элемента. Эти события независимы (по условию).

а) Одновременное появление А и В есть событие АВ. Следовательно,

.

б) Если работает первый элемент, то имеет место событие   (противоположное событию А- выходу этого элемента из строя); если работает второй элемент- событие В. Найдем вероятности событий   и  :

;

.

Тогда событие, состоящее в том, что будут работать оба элемента, есть   и, значит,

.
Контрольные вопросы
1. Какие виды событий вы знаете? Дайте определение каждому из них.

2. Что называется вероятностью случайного события?

3. В чем заключается геометрический способ определения вероятности?

4. Какие комбинации элементов называются перестановками, размещениями,

сочетаниями?

5. Что называется суммой случайных событий? Произведением случайных

событий?
Примеры тестовых заданий
Случайное событие, это такое событие

• 
  . причины которого неизвестны
  
• 
  . если условия, в которых оно происходит, различны
  
• 
  . закономерности которого не поддаются наблюдению
  
• 
  . которое при совокупности одних и тех же условий может произойти, а может не произойти
  

События называются несовместными, если

• 
  . в данном опыте они могут появиться все вместе
  
• 
  . сумма вероятностей их равна единице
  
• 
  . хотя бы одно из них не может появиться одновременно с другим
  
• 
  . в одном и том же опыте появление одного из них исключает появление других событий
  

Суммой, (объединением) нескольких случайных событий называется

• 
  . событие, состоящее в появлении любого из этих событий
  
• 
  . событие, состоящее в появлении всех указанных событий
  
• 
  . событие, состоящее в появлении хотя бы одного из этих событий
  
• 
  . событие, состоящее в появлении одного из этих событий
  

Произведением, совмещением, нескольких событий называется

• 
  . событие, состоящее в осуществлении любого из этих событий;
  
• 
  . событие, состоящее в появлении хотя бы одного из этих событий;
  
• 
  . состоящее в последовательном появлении всех этих событий;
  
• 
  . состоящее в осуществлении одновременно всех этих событий.
  

Классическое определение вероятности события А состоит в том, что вероятность события А есть . отношение общего числа исходов к числу исходов, благоприятствующих событию А . отношение числа благоприятствующих этому событию исходов, которые могут быть совместны и равновозможны, к общему числу всех возможных исходов . отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных элементарных исходов, образующих полную группу событий . отношение числа благоприятствующих этому событию исходов к общему числу всех одинаковых исходов.

5.Понятие случайной величины. Виды событий. Вероятность события Функция распределения

Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием.

Результат этого действия или наблюдения называется событием.

Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти,- невозможным.

События называются несовместными, если каждый раз возможно появление только одного из них.

События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.

События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.

События принято обозначать заглавными буквами латинского алфавита: А, В, С, Д, : .

Полной системой событий А₁, А₂, А₃, : , А_n называется совокупность несовместных событий, наступление хотя бы одного из которых обязательно при данном испытании.

Если полная система состоит из двух несовместных событий, то такие события называются противоположными и обозначаются А и  .

Пример. В коробке находится 30 пронумерованных шаров. Установить, какие из следующих событий являются невозможными, достоверными, противоположными:

достали пронумерованный шар (А);

достали шар с четным номером (В);

достали шар с нечетным номером (С);

достали шар без номера (Д).

Какие из них образуют полную группу?

Решение. А - достоверное событие; Д - невозможное событие;

В и С - противоположные события.

Полную группу событий составляют А и Д, В и С.

Вероятность события, рассматривается как мера объективной возможности появления случайного события.

Случайной величиной называется такая переменная величина, которая в результате проведения опыта может принять то или иное значение, неизвестное до проведения эксперимента.

Случайные величины принято обозначать заглавными, последними буквами латинского алфавита , , , …, а значения, которые они могут принять обозначают аналогичными, но прописными буквами , , , … XYZ xyz

Пример 1. Являются ли случайными величинами следующие переменные величины: а) число вызовов, поступивших от абонентов на телефонную станцию в течение определенного промежутка времени; б) число электронов, вылетевших из нагретого катода за определенный промежуток времени; в) длина некоторой детали при массовом производстве (самостоятельно).

Все случайные величины делятся на три группы: дискретные, смешанные и непрерывные. В Примере 1 случаи а) и б) указывают на случайные дискретные величины, а случай в) – на случайную непрерывную величину.

Законом распределения случайной величины называется любое соотношение, с помощью которого устанавливается соответствие между возможными значениями случайной величины и вероятностями некоторых событий, связанных определенным образом с этими возможными значениями.
Закон распределения случайной величины может быть представлен аналитической формулой ; графиком, связывающим значения вероятности со значениями случайной величины; таблицей, которая устанавливает соответствие между значениями случайной величины и их вероятностями.

В определение закона распределения случайной величины входят слова

“любое соотношение” – это означает, что таких соотношений может быть очень

много. К числу универсальных форм закона распределения случайной величины относится функция распределения.

Функцией распределения случайной величины называется вероятность события , которое состоит в том, что случайная величина обязательно примет значение заведомо меньшее, чем заданное значение

Пример 2. Найти функцию распределения случайной величины, которая представляет собой значение определенной грани кубика.

Рассмотрим события, определяющие случайную дискретную величину, и вероятности этих событий:

• 
  данное событие является невозможным, так как на гранях кубика нет числа, которое было бы меньше единицы, а вероятность невозможного события равна нулю отметим, что любое событие является невозможным событием, поэтому вероятность такого события равна нулю;
  
• 
  данное событие является достоверным, так как в этом случае обязательно выпадет одно из чисел от 1 до 6, а вероятность достоверного события равна 1
  

для любого другого числа событие будет достоверным событием, следовательно, вероятность такого события будет равна единице.

Случайная дискретная величина характеризуется функцией распределения, график которой имеет “ступенчатый” вид. Случайная непрерывная величина характеризуется функцией распределения, график которой имеет “непрерывный” вид

Лекция 7