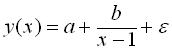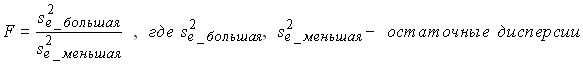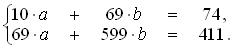эконометрика. Линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a b уравнения по выборке объема n имеет вид
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
Если связь между факторами близка к функциональной, то определитель матрицы парных межфакторных коэффициентов корреляции
Нулевая гипотеза о статистической незначимости уравнения регрессии отклоняется, если
Пусть: при 5%-ом уровне значимости DWu и DWl – верхняя и нижняя границы критерия Дарбина-Уотсона; DW – фактическое значение критерия. Нулевая гипотеза об отсутствии автокорреляции в остатках не отклоняется при условии: Значимость дополнительных факторов, включаемых в эконометрическую модель с целью улучшения модели, можно оценить с помощью
В основе метода наименьших квадратов (МНК) лежит минимизация выражения По 30-ти наблюдениям построено уравнение регрессии
Если средние квадратические отклонения наблюдаемых значений факторного признака X и результирующего признака Y от и
По последовательности коэффициентов автокорреляции уровней временного ряда и соответствующим значениям лага строят
Условие независимости дисперсии остатков от номера наблюдения (постоянство дисперсии) называют
Для оценки значимости параметров множественной линейной регрессии используют критерий
Вопрос №3 Уровень сложности - тяжёлый (3 балла) Для эконометрической модели, выраженной системой уравнений
Для оценки структурных параметров сверхидентифицируемых эконометрических моделей, выраженных системами одновременных уравнений, можно пользоваться
При использовании шагового регрессионного анализа при выборе наилучшей эконометрической регрессионной модели процедура включения нового фактора в модель завершается, если включение фактора
По 25-ти наблюдениям построено уравнение регрессии
Пусть: Y – признак-результат; При моделировании сезонных колебаний в динамике показателя номер поворотной точки на ломаной, изображающей соответствующий временной ряд за несколько лет, совпадает
Если рассчитанные значения компонент временного ряда позволяют представить уровни ряда в виде произведения тенденции ряда, периодических колебаний и случайных колебаний, то построенная модель ряда называется
Регрессией, нелинейной относительно включенных в анализ объясняющих переменных, но линейных по оцениваемым параметрам, является уравнение: Если 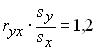 , то параметр a в уравнении парной линейной регрессии , то параметр a в уравнении парной линейной регрессии
Пусть: при 5%-ом уровне значимости DWu и DWl – верхняя и нижняя границы критерия Дарбина-Уотсона; DW – фактическое значение критерия. Нельзя ни отклонить, ни принять нулевую гипотезу об отсутствии автокорреляции в остатках при условии: Исследование стабильности дисперсии случайного члена в регрессионной модели сводится к проверке статистической гипотезы о равенстве двух дисперсий (вычисленных по группе первых наблюдений и по группе последних наблюдений) с использованием статистики: Если: объем выборки равен 10, Система эконометрических уравнений 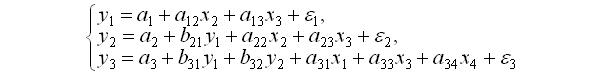 является примером систем является примером систем
Если число коэффициентов эконометрической структурной модели меньше числа коэффициентов соответствующей приведенной модели, то структурная модель называется
При моделировании тенденции в динамике показателя уравнением 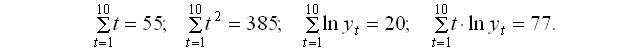 Тогда оценки параметров тренда Тогда оценки параметров тренда
Если значение выборочного коэффициента парной линейной корреляции значимо и является отрицательным числом, то
Матрица парных коэффициентов корреляции –
|

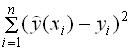 как
как