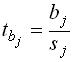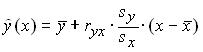эконометрика. Линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a b уравнения по выборке объема n имеет вид
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
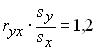 , то параметр a в уравнении парной линейной регрессии , то параметр a в уравнении парной линейной регрессии
Вычислены частные коэффициенты линейной корреляции первого порядка:
Уравнение парной линейной регрессии имеет вид: Метод наименьших квадратов позволяет получить такие оценки параметров уравнения регрессии, при которых
По 30-ти наблюдениям построено уравнение регрессии
Если критическое (табличное) значение F–критерия (критерия Фишера) равно числу 6.12, то нулевая гипотеза о статистической незначимости уравнения регрессии отклоняется в пользу конкурирующей гипотезы при условии: Наиболее вероятно, что временной ряд характеризуется наличием тенденции в динамике изучаемого показателя при следующих значениях коэффициентов автокорреляции: По 30-ти наблюдениям построено уравнение регрессии
Для сопоставления факторов по силе влияния на изменение признака-результата можно пользоваться
При проверке нулевой гипотезы о несмещенности случайных отклонений Косвенный метод наименьших квадратов применим к вычислению структурных коэффициентов систем одновременных уравнений, выражающих Средние значения оценки периодической компоненты для данного временного ряда составили: Система шести одновременных эконометрических уравнений включает m экзогенных переменных. Условие неидентифицируемости уравнения В уравнении регрессии
Если наблюдается непрерывный рост уровней показателя со снижающимися темпами роста, то модель тенденции в динамике показателя можно выразить уравнением: Факторная (объясненная) сумма квадратов отклонений для регрессии вычисляется по формуле: В множественной регрессии показателями тесноты корреляционной связи являются
По 14-ти наблюдениям построено уравнение регрессии
Матрица коэффициентов при эндогенных переменных приведенной формы эконометрической модели может иметь вид: За последовательные 3 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты: 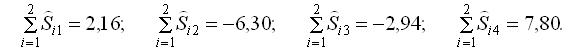 Корректирующий показатель для определения значений сезонной компоненты равен Корректирующий показатель для определения значений сезонной компоненты равен
Наиболее вероятно, что временной ряд характеризуется наличием периодических колебаний в динамике изучаемого показателя при следующих значениях коэффициентов автокорреляции: По последовательности коэффициентов автокорреляции уровней временного ряда и соответствующим значениям лага строят
Пусть: Y – признак-результат; Если: n – объем выборки, Система линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a,b уравнения 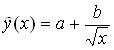 по выборке объема n имеет вид: по выборке объема n имеет вид:За последовательные 4 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты: 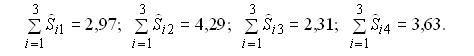 Скорректированные значения сезонной компоненты равны соответственно: Скорректированные значения сезонной компоненты равны соответственно:Если:
Для оценки структурных параметров сверхидентифицируемых эконометрических моделей, выраженных системами одновременных уравнений, можно пользоваться
Оценивание качества уравнения регрессии состоит
Для нелинейной модели с помощью МНК построено уравнение регрессии и вычислены значения величин: 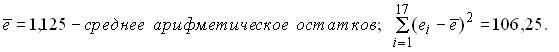 Табличное значение приемлемого статистического критерия равно 2,1. Следовательно, нет оснований отклонять предположение Табличное значение приемлемого статистического критерия равно 2,1. Следовательно, нет оснований отклонять предположение
Коэффициент парной линейной корреляции
Фактическое значение критерия Стьюдента (t-критерия) для параметра Если вычислены значения величин: Вычислены частные коэффициенты линейной корреляции первого порядка:
Если наблюдаются стабильные темпы роста показателя, то модель тенденции в динамике показателя можно выразить уравнением: В уравнение множественной регрессии должны быть включены факторы, которые
Вычислены частные коэффициенты линейной корреляции первого порядка:
Для линейной регрессионной модели с помощью МНК построено уравнение регрессии и вычислено значение величины: 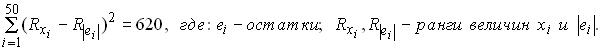 Табличное значение критерия Стьюдента на уровне значимости 0,05 равно 2,01. Следовательно, отклоняется предположение об отсутствии Табличное значение критерия Стьюдента на уровне значимости 0,05 равно 2,01. Следовательно, отклоняется предположение об отсутствии
За последовательные 3 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты: 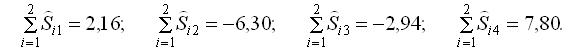 Корректирующий показатель для определения значений сезонной компоненты равен Корректирующий показатель для определения значений сезонной компоненты равен
Для эконометрической модели, выраженной системой уравнений в отклонениях переменных от их средних уровней 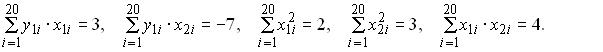 Тогда приведенное уравнение регрессии для эндогенной переменной имеет вид: Тогда приведенное уравнение регрессии для эндогенной переменной имеет вид:При использовании метода последовательного включения факторов в уравнение множественной регрессии целесообразность включения нового фактора оценивается с точки зрения сокращения
Для линейной модели регрессии с помощью МНК построено уравнение регрессии и вычислено значение величины:  Табличное значение критерия Стьюдента на уровне значимости 0,05 равно 2,03. Следовательно, нет оснований отклонять предположение Табличное значение критерия Стьюдента на уровне значимости 0,05 равно 2,03. Следовательно, нет оснований отклонять предположение
Если эконометрическая модель строится в виде системы рекурсивных уравнений, то параметры системы можно определить
Корреляционная зависимость между значениями случайных остатков
Средние значения оценки периодической компоненты для данного временного ряда составили: Нарушение условия независимости дисперсии остатков
Проверка значимости уравнения Для линейной модели регрессии с помощью МНК построено уравнение регрессии и вычислено значение величины:  Табличное значение критерия Стьюдента на уровне значимости 0,05 равно 2,03. Следовательно, нет оснований отклонять предположение Табличное значение критерия Стьюдента на уровне значимости 0,05 равно 2,03. Следовательно, нет оснований отклонять предположение
Индекс детерминации характеризует
Для обеспечения статистической достоверности множественной линейной регрессии количество наблюдений должно превышать количество параметров, не считая свободного члена,
Зависимые переменные в системе одновременных эконометрических уравнений – это переменные
Результатом преобразования уравнения Если рассчитанные значения компонент временного ряда позволяют представить уровни ряда в виде произведения тенденции ряда, периодических колебаний и случайных колебаний, то построенная модель ряда называется
Если сумма квадратов отклонений значений признака-результата Y от его среднего уровня равна 5.7, а остаточная сумма квадратов отклонений для уравнения множественной регрессии равна 0.9, то степень тесноты связи признака Y с набором признаков-факторов, включенных в модель регрессии, можно оценить (с точность 0,01) числом
Если значение критической точки, найденное по таблице «Критические точки распределения Стьюдента », равно 1.78, то нулевая гипотеза об отсутствии линейной корреляционной связи между признаками X и Y отклоняется в пользу конкурирующей гипотезы при: Фактическое значение критерия Стьюдента (t-критерия) для параметра |

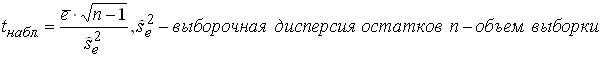
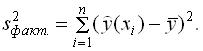

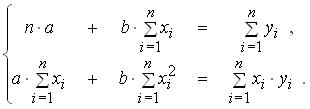
 \
\