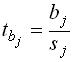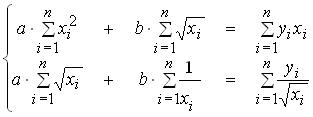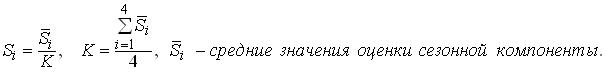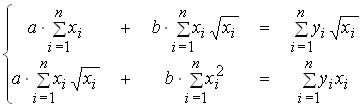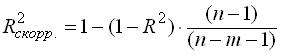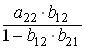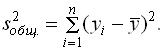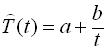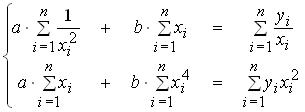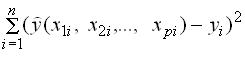эконометрика. Линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a b уравнения по выборке объема n имеет вид
 Скачать 1.05 Mb.
|
 множественной линейной регрессии, вычисленного со стандартной ошибкой , вычисляют по формуле:При использовании метода исключения факторов при выборе наилучшей эконометрической регрессионной модели процедура последовательного исключения факторов из модели повторяется до тех пор, пока текущая модель регрессии не будет иметь Для эконометрической модели, выраженной системой уравнений  коэффициент при  во втором уравнении приведенной формы модел
Приведенная форма некоторой структурной модели может быть выражена системой уравнений: Система линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a,b уравнения 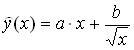 по выборке объема n имеет вид:Если  , ( – значения стандартизованных коэффициентов множественной линейной регрессии), то степень тесноты линейной связи признака-результата Y с набором признаков-факторов , учтенных в модели регрессии, можно оценить (с точность 0,01) числом
По 27-ти наблюдениям за изменениями значений признаков X и Y вычислено значение парного коэффициента линейной корреляции. Распределение значений статистической характеристики нулевой гипотезы об отсутствии линейной корреляционной зависимости между признаками X и Y близко к распределению
Если сумма квадратов отклонений значений признака-результата Y от его среднего уровня равна 13.7, а остаточная сумма квадратов отклонений для уравнения множественной регрессии равна 1.3, то степень тесноты связи признака Y с набором признаков-факторов, включенных в модель регрессии, можно оценить (с точность 0,01) числом
Пусть: Y – признак-результат;  –признаки - факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков  от средних уровней признаков и построено уравнение регрессии в стандартизованном масштабе Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:При построении мультипликативной модели уровня временного ряда скорректированное значение сезонной компоненты вычисляют по формуле: Система линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a,b уравнения  по выборке объема n имеет вид:Проверка значимости выборочного коэффициента парной линейной корреляции требует проверки статистической гипотезы: Если для оценки параметров уравнения регрессии использован метод наименьших квадратов (МНК), то требуется, чтобы математическое ожидание остатков 
По 25-ти наблюдениям построено уравнение регрессии  . Коэффициент линейной корреляции составил 0,65. После включения в модель фактора  индекс множественной корреляции составил 0,7. На уровне значимости 0,05 табличное значение F-критерия равно 4,3. Включение в эконометрическую модель фактора незначимо, так как фактическое значение частного F-критерия равно
Для нелинейной модели с помощью МНК построено уравнение регрессии и вычислены значения величин: 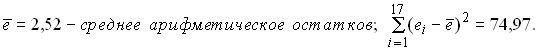 Табличное значение приемлемого статистического критерия равно 2,1. Следовательно, отклоняется предположение о
При построении уравнения регрессии по наблюдаемым значениям признаков X и Y с применением метода наименьших квадратов уравнение  следует преобразовать к виду:Дана система одновременных эконометрических уравнений: 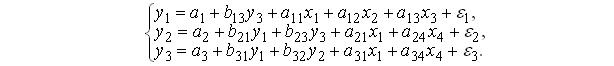 Для первого уравнения системы
Пусть: Y – признак-результат; –признаки - факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков и построено уравнение регрессии в стандартизованном масштабе Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:Пусть: n– количество наблюдений, m – число параметров при факторах уравнения множественной регрессии. Скорректированный индекс детерминации  связан с индексом детерминации равенством:При использовании шагового регрессионного анализа при выборе наилучшей эконометрической регрессионной модели добавление нового фактора требует проверки значимости
Пусть: при 5%-ом уровне значимости DWu и DWl – верхняя и нижняя границы критерия Дарбина-Уотсона; DW – фактическое значение критерия. Нулевая гипотеза об отсутствии автокорреляции в остатках отклоняется при условии: Последовательность коэффициентов автокорреляции уровней временного ряда с возрастающими значениями лага называют функцией
Для проверки значимости выборочного коэффициента парной линейной корреляции используют критерий
По значениям показателя за 12 кварталов 2007г., 2008г., 2009г. построена модель временного ряда. Модель тренда выражена уравнением:  Вычислены следующие значения сезонной составляющей:  Прогнозируемое значение показателя на 2-ой квартал 2010 года равно
Вычислены частные коэффициенты линейной корреляции первого порядка:  Тогда частный коэффициент линейной корреляции второго порядка  равен
Индекс детерминации характеризует
Система шести одновременных эконометрических уравнений включает m экзогенных переменных. Условие неидентифицируемости уравнения  выполняется приЕсли:  , то можно считать, что между значениями признаков X и Y
Для эконометрической модели, выраженной системой уравнений  коэффициент  при в первом уравнении приведенной формы модели
Общая сумма квадратов отклонений для регрессии вычисляется по формуле: Уравнение  , отражающее корреляционную связь между признаком-результатом Y и признаками-факторами , это –
Если коэффициент парной линейной корреляции  равен 0.7, то доля вариации зависимого признака Y, объясняемой изменением факторного признака X, составляет
При стремлении уровней показателя к «уровню насыщения» модель тенденции в динамике показателя можно выразить уравнением: При расчете значений сезонной компоненты в модели уровня временного ряда корректирующий показатель вычисляют по формуле: При использовании метода исключения факторов при выборе наилучшей эконометрической регрессионной модели процедура последовательного исключения факторов из модели повторяется до тех пор, пока текущая модель регрессии не будет иметь
Система линейных алгебраических уравнений для определения методом наименьших квадратов значений параметров a,b уравнения  по выборке объема n имеет вид:При определении параметров тренда временного ряда методом наименьших квадратов зависимой переменной является
Пусть: Y – признак-результат; –признаки - факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков и построено уравнение регрессии в стандартизованном масштабе  Тогда теоретические (расчетные) значения признака-результата вычисляют по формуле:При построении уравнения регрессии по наблюдаемым значениям признаков X и Y с применением метода наименьших квадратов уравнение  следует преобразовать к виду:Исследование стабильности (постоянства) дисперсии случайных отклонений в моделях регрессии сводится к проверке статистической гипотезы о равенстве
Измерителями степени тесноты корреляционной связи между признаком-результатом Y и признаками-факторами  являются показатели, вычисленные по n наблюдениям и в основе которых лежит значение величины:Если, выборочные средние квадратические отклонения значений результирующего признака Y и факторного признака X от  равны 2,4 и 1,2 соответственно, то уравнением парной линейной регрессии может быть уравнение:Приведенная форма некоторой структурной модели может быть выражена системой уравнений: При построении моделимножественной регрессии выявление корреляционных связей между признаком-результатом и признаками-факторами происходит на этапе
Если число коэффициентов эконометрической структурной модели больше числа коэффициентов соответствующей приведенной модели, то структурная модель называется
Критерием отбора наилучшей формы тренда временного ряда
Основой проверки значимости построенной регрессии и ее параметров по общему F-критерию является
Если остатки и  не коррелированны между собой при ,  то:
По значениям показателя за 12 кварталов 2007г., 2008г., 2009г. построена модель временного ряда. Модель тренда выражена уравнением:  Вычислены следующие значения сезонной составляющей:  Прогнозируемое значение показателя на 3-ий квартал 2010 года равно
Недостающим элементом в формуле коэффициента парной линейной корреляции  являетсяПусть: Y – признак-результат; –признаки - факторы. По исходным данным вычислены средние уровни признаков и средние квадратические отклонения значений признаков от средних уровней признаков: |
равно нулю при
