отчет по производственной практике кб кубань кредит. Пальчик Олеся, БД-2-9А-17. "Линейное программирование. Виды задач линейного программирования. Линейное программирование в банковском деле."
 Скачать 66.56 Kb. Скачать 66.56 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЕЖНОЙ ПОЛИТИКИ КРАСНОДАРСКОГО КРАЯ государственное автономное профессиональное образовательное учреждение Краснодарского края «Краснодарский информационно-технологический техникум» Лицензия серия 23Л01 № 0004947 рег. № 08112 от 14.10.2016 г. Гос. аккредитация 23А01 № 0001576 рег. № 03793 от 26.04.2018 г. 350072г. Краснодар, ул. Московская, 81, тел (861) 252-03-83 Реферат На тему: "Линейное программирование. Виды задач линейного программирования. Линейное программирование в банковском деле." Выполнила : Пальчик Олеся Викторовна Студентка группы БД-2-9А-17 Преподаватель : Маслова Ирина Валентиновна Краснодар 2019 СОДЕРЖАНИЕ
ВВЕДЕНИЕ термин «программирование» нужно понимать в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации. В 1939 году Леонид Витальевич Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования. Джордж Данциг разработал симплекс-метод и считается «отцом линейного программирования» на западе Каждый человек ежедневно, не всегда осознавая это решает проблему: как получить наибольший эффект, обладая ограниченными средствами. Чтобы добиться наибольшего эффекта, имея ограниченные средства, надо составить план, или программу действий. Раньше план в таких случаях составлялся "на глазок". В середине XX века был создан специальный математический аппарат, помогающий это делать "по науке". Соответствующий раздел математики называется математическим программированием. Слово "программирование" здесь и в аналогичных терминах ("линейное программирование, динамическое программирование" и т.п.) обязано отчасти историческому недоразумению, отчасти неточному переводу с английского. По − русски лучше было бы употребить слово "планирование". С программированием для ЭВМ математическое программирование имеет лишь то общее, что большинство возникающих на практике задач математического программирования слишком громоздки для ручного счета, решить их можно только с помощью ЭВМ, предварительно составив программу. 1 Методы линейного программирования Линейное программирование − это раздел математического программирования, применяемый при разработке методов нахождения экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По характеру решаемых задач методы линейного программирования можно разбить на несколько групп, в соответствии с рисунком 1.  1. Универсальные методы. С их помощью могут решаться любые задачи линейного программирования. Самым распространенным из них является симплексный метод, предложенный Дж. Данцигом, метод разрешающих множителей, разработанный академиком Л. В. Канторовичем в 1939 г., примерно за 10 лет до его появления за рубежом. 2. Специальные методы. Эти методы проще универсальных, но применимы не для всех задач. К ним относятся распределительный метод, метод разрешающих слагаемых А. Л. Лурье, метод дифференциальных рент А. Л. Брудно. Главная особенность задач линейного программирования заключается в том, что экстремум целевой функции находится на границе области допустимых решений. 2 Задачи линейного программирования Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств. Кратко задачу линейного программирования можно сформулировать следующим образом: найти вектор значений переменных, доставляющих экстремум линейной целевой функции при m ограничениях в виде линейных равенств или неравенств. Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи: − рационального использования сырья и материалов; задачи оптимизации раскроя, − оптимизации производственной программы предприятий, −оптимального размещения и концентрации производства, − составления оптимального плана перевозок, работы транспорта, − управления производственными запасами, −и многие другие, принадлежащие сфере оптимального планирования. Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального). В общей постановке задача линейного программирования выглядит следующим образом: Имеется переменная х = ( 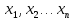 ) и функция этих переменных f(x) = ( ) и функция этих переменных f(x) = (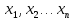 ), которая называется целевая функция. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные х принадлежат некоторой области G: ), которая называется целевая функция. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные х принадлежат некоторой области G: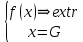 В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. а)функция f(x) является линейной функцией переменных ( 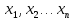 ) )б)область G определяется системой линейных равенств или неравенств. Математическая модель любой задачи линейного программирования включает в себя: Нахождения минимума линейной целевой функции вида: 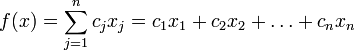 Задача в которой фигурируют ограничения в форме неравенств, называется — основной задачей линейного программирования. 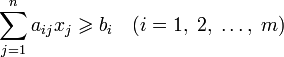 2.1 Каноническая задача линейного программирования Система ограничений в задаче линейного программирования в канонической форме записывается так: 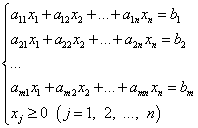 Или в сокращённом виде: 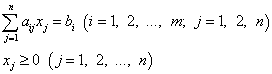 И система ограничений, и целевая функция имеют линейный характер, то есть содержат переменные только в первой степени. Канонической задачей линейного программирования называется задача, в которой, как было показано выше, требуется найти максимум целевой функции при ограничениях, заданных системой линейных уравнений. 2.2 Симплекс − метод решения линейных задач Симплекс-метод позволяет переходить от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают. Алгоритмы симплекс-метода позволяют также установить, является ли задача ЛП разрешимой. Переход от одного базиса к другому позволяет находить решения почти всех задач ЛП. Определив все крайние точки, можно вычислить значения целевой функции и найти оптимальное решение. Однако для больших значений m и n это практически невозможно. Алгоритм решения задачи ЛП табличным симплексом-методом состоит из следующих этапов: 1. рассчитывают и заполняют начальную симплекс-таблицу с допустимым единичным базисом, включая индексную строку. 2. находят разрешающий столбец; 3. находят разрешающую строку; 4. рассчитывают методом Жордано-Гаусса все параметры матрицы; 5. анализируют полученные данные в индексной строке. Таблицы симплекс-метода необходимо строить до тех пор, пока не будет получен оптимальный план. План будет считаться оптимальным, если в последней индексной строке симплекс-таблицы будут только нули и положительные числа. 3 Линейное программирование в банковском деле Модель линейного программирования выражает взаимосвязь различных элементов принятия решения в стандартной математической форме. Цель решения может состоять, например, в максимизации прибыли, минимизации риска и издержек и т. д. Применение данного метода базируется на использовании современных ЭВМ, программного обеспечения. Работа банка по размещению имеющихся в его распоряжении ресурсов составляет основу его активных операций. Планирование активных операций банка состоит в целесообразном размещении собственных и привлеченных средств с целью получения наивысшей доходности. При планировании размещения банковских ресурсов следует придерживаться принципов указанных в таблице 1 Таблица 1 − Принципы размещения банковских ресурсов
Рассмотрим математические модели некоторых важных экономических задач. Пусть собственные средства банка в сумме с депозитами составляют 100 млн долл. Часть этих средств, но не менее 35 млн долл., должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, т.к. в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно. Другое дело ценные бумаги (особенно государственные). Их можно в любой момент продать, получив некоторую прибыль, или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определённой пропорции ликвидные активы – ценные бумаги, чтобы компенсировать не ликвидность кредитов. В нашем примере ограничение таково: ценные бумаги должны составлять не менее 30% средств, размещённых в кредитах и ценных бумагах. Пусть х – средства (млн долл.), размещённые в кредитах, у – средства, вложенные в ценные бумаги. Имеем следующую систему ограничений: Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг: при условии 1)-4), где Т.к. кредиты менее ликвидны, чем ценные бумаги, то обычно Пусть собственные средства банка в сумме с депозитными составляют 100 млн д.е.. Часть этих средств, но не менее 35 млн д.е., должна быть размещена в кредитах. Кредиты должны быть неликвидными активами банка, так как в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно. Другое дело ценные бумаги, особенно государственные. Их можно в любой момент продать, получив некоторую прибыль или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы – ценные бумаги, чтобы компенсировать не ликвидность кредитов. В нашем примере ликвидное ограничение таково: ценные бумаги должны составлять не менее 50% средств, размещенных в кредитах и ценных бумагах. Составим математическую модель задачи. Обозначим через x1 – средства в млн д.е., размещенные в кредитах, x2 – средства, вложенные в ценные бумаги. Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг: L=c1x1+c2x2→(max), где c1 – доходность кредитов; c2 – доходность ценных бумаг. Так как кредиты менее ликвидны, чем ценные бумаги, то обычно c1>c2. Учитывая балансовое, кредитное и ликвидное ограничения, получим систему ограничений неравенств 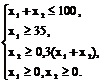 Замечание. Система ограничений, в зависимости от условий задачи, может содержать не только линейные неравенства, но и линейные уравнения. ЗАКЛЮЧЕНИЕ Серьезной проблемой при практическом применении линейного программирования в решении экономических задач называется большой объем информации, необходимый для передачи данных от субъектов хозяйствования к планирующему органу и обратно. Считается, что наличие денег позволяет уменьшить эти объемы, упростить передачу и обработку информации. В противоположность этому, считается, что расчет в натуральных показателях потребует не только больших вычислительных ресурсов, но и высоких требований к коммуникационным системам. СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ Основная литература 1. Хазанова Л.Э. Математическое моделирование в экономике. М.: Изд-во БЕК, 1998. 2. Патыка Т.Л., Попов И.И. Математические методы: Учебник, 2005. Интернет − ресурсы 1. История линейного программирования режим доступа : https://stydopedia.ru/2x1fca.html 2. Виды задач линейного программирования режим доступа : https://function-x.ru/zadacha_lineinogo_programmirovanija.html 3.Линейное программирование режим доступа : https://helpiks.org/8-60929.html |
