Лин(вное)прво. Лин подпрво
 Скачать 446.05 Kb. Скачать 446.05 Kb.
|
базис зад. пр-ва,а b произвол. ненул. в-р этого пр-ва. Рас.лин.комбинацию.λ0*b+λ1*a1+λ2*a2+…+λnan=0Система из более, чем одного вектора линейно-зависима , когда хотя бы 1 из в-ров есть лин.комбинация остальных. Если в сис.входит нул.в-р ,то она л.з. Если некот.из в-ров входящих в сис.образует л.з.подсистему,то вся сис. л.з. Видим, что λ0≠0. В противном случае сис.будет л.з. b=- 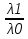 *а1- *а1-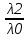 *а2-…- *а2-…-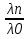 *аn= *аn=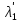 *а1+ *а1+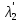 *a2+…+ *a2+…+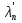 *an *an Т.о.лин.представление возможно. ] оно не единственно. И в-р b разложен по базису 2 сп-бами: b= 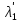 *а1+…+ *а1+…+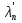 *an и b= *an и b=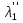 *а1+…+ *а1+…+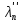 *an . вычитая из 1 2 получим ( *an . вычитая из 1 2 получим (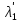 - -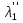 )*a1+…+( )*a1+…+(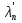 - -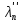 ) *an=0 ) *an=0Но, если хоть 1 из разностей в скобках≠0, то векторы a1,a2 . . . , ап – л.-з., что противоречит условию. Т. док-на. В соответствии с Т. любой в-р х лин. про-ва L мб единств. образом представлен в виде х=х1а1+х2а2+…+хпаn,где а1,а2,…,аn базис пр-ва L,такое разложение наз.разложением в-ра х по базису а1,а2,…,аn,а числа х1,х2,…,хn- коор.в-ра х относит.в-ра базиса а1,а2,…,аn Оказывется, что единств.разложения произвольного в-ра пр-ва по нек-рой сис.в-ров Snявл. признаком базиса. Т.Пусть по системе векторов S n : a1, a2, ... ,an можно единств. образом разложить любой в-р пр-ва L . Тогда данная сис. в-ров образует базис. Линейная оболочка векторов.Линейная оболочка — это набор векторов, которые задают линейное подпространство. линейная оболочка — это множество всех линейных комбинаций данных векторов.Если задана лин.оболочка — ранг набора векторов равен его размерности. Векторное представление системы линейных уравнений. Представим осн. матрицу А в виде в-р-столбцов А1, А2,…, Ап. Тогда система лин. ур-ний (6.1) записывается в векторном виде: x1А1+х2А2+…+хnAn=b А1=( 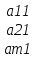 , )A2=( , )A2=(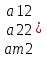 ,…. An=( ,…. An=(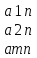 ),b=( ),b=(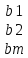 ) )Значит, сис. лин. ур-ний тхп мб представлена в виде разложения в-а b€Rm – в-ра свободных членов по n в-рам А1, А2, . . . , А п € R m – в-р-столбцам матрицы коэф., при этом коэф. разложения оказываются переменные. Теорема Кронекера-Капелли. Для того, чтобы сис. лин. ур-ний ( 6 .1 ) имела решения, необ. и дост., чтобы ранг осн. матрицы равнялся бы рангу расш. матрицы. Необходимость. Пусть сис. имеет решение 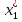 , ,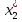 ,…, ,…,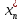 тогда в-рная форма сис.лин. ур-ний имеет вид: тогда в-рная форма сис.лин. ур-ний имеет вид: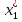 А1+ А1+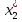 А2+…+ А2+…+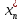 An=b An=bоткуда следует, что в-р bлинейно выражается через векторы А1, А2, ... ,Ап ранги систем S = { А1, А2, …, Ап} и S={S,b}равны. Из т. о равенстве ранга матрицы макс. числу её лин. нез. столбцов ,получим, что ранг осн. Матрицы=рангу расш. Достаточность. ] ранги расш. и осн. матриц равны,то и ранги систем S и S тоже равны. Тогда лин. оболочки L (S )и L (S ) сис. S и S совпадают. По опред. лин. оболочки всякий её в-рпредставим в виде лин. ком-ции в-ров, образующих эту сис., т.е. сущ. набор чисел 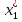 , ,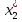 ,…, ,…,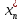 , что , что 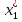 А1+ А1+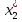 А2+…+ А2+…+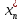 An=b. An=b.Но тогда числа 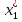 , ,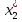 ,…, ,…,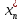 как раз и явл. решением сис.ч.т.д. как раз и явл. решением сис.ч.т.д.Критерий линейной зависимости векторов в пространстве Rn. Если ранг матрицы коорд. = числу в-ров,то эти в-ра лин. нз., если меньше, то эти в-ра лин.зав. Док-во: Расм.лин.комб. в-ров сист.Sn вида: α1a1+…+αnan=α1*( 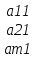 )+…+α*=( )+…+α*=(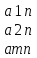 )=0,где α1,…, αn-вещ.числа. )=0,где α1,…, αn-вещ.числа.Данное выр-е можно представить виде сист.лин.однородных ур-й. α1а11+α2а12+…+α1а1n=0 α1а21+α2а22+…+α1а2n=0 α1аm1+α2аm2+…+αmamn=0 Эта сист.всегда имеет реш-е.Имеется бескон. много реш-й в том случае,если ранг основ.матр., к-рая в дан. случае совпадает с матр.коорд., меньше числа неизв.,число к-рых=числу в-ров.Среди бескон.мн-ва реш-й имеется и нетривиал.показыв.лин.зав.в-ров.Если ранг матр.коорд. = числу в-ров, то имеется только одно тривиал. реш-е, говорящее о лин. незав.в-ров. ч.т.д. Евклидовое пространство.Лин. пр-во наз.евклидовым, если для любых 2х в-ров х, у этого пр-ва задано правило, по к-рому дан.в-рам сопоставляется число, обозначаемое как (х ,у ), удовлетворяющее след. св-вам скал. пр-ния:1.(х ,у ) = (у,х). 2Для любого вещ.числа λ€R,(λх,у)=λ(у,х) 3. (х+у,z) = (x ,z )+(y ,z). 4 (x,x)≥0 ,если (x,x)=0, то обязательно х=0 Т.для любых 2 в-ров х,у евклидово пр-во справедливо нерав-но (х,у)2≤(х,х)(у,у) для любого вещ. числа t в силу аксиомыи4 скал. произведения будет (х + tx ,x + tx )≥0, раскрывая скобки, получим (х+ty,x+ty)=(x,x)+2t(x,y)+t2(y,y)≥0 Левую часть нерав-ва можно рассматривать как квадрат. 3хчлен по перем. t. Он неотриц, если дискрим. не полож:D=4(x,y)2-4(x,x)2(y,y)≤0 или (х,у)2≤(х,х)(у,у) Доказанное нерав-во наз. неравенством Коши-Буняковского Нормированное пространство Лин. пр-во наз. нормируемым, если любому в-ру х этого пр-ва сопоставлена норма ||х|| - числа, к-рое удовл. след. св-вам: 1. ||х|| ≥0, если||х|| =0, то обязательно х=0. 2. Для люб. вещ.числа λ €R, ||λх|| = |λ|*||x||. 3. Для любых 3х эл-тов x ,y ,z этого пр-ва справедливо нерав-во треуг-ника: ||x+y||= ||x||+ ||у||. Если ||x||(€R) -норма х и ||x||= 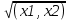 тогда св-во 1-3 выполн.-->всякого евклидово пр-во нормируемо. тогда св-во 1-3 выполн.-->всякого евклидово пр-во нормируемо.Ортогональное дополнение и его свойства. Ортог. Дополнением дан. подпр-тва наз.множество всех в-ров, ортогональных каждому в-ру из дан.подпр-ва. Т.Ортог. дополние подпр-ва явл. подпр-вом. Док-во. Если х ,у € 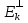 , то для любого z€Ек получим (x,z)=0и (у, z) = 0. Откуда следует, что и х + у и λх € , то для любого z€Ек получим (x,z)=0и (у, z) = 0. Откуда следует, что и х + у и λх € 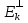 , т.к. для люб. z€Ек и λ€R по опр.множ-ва , т.к. для люб. z€Ек и λ€R по опр.множ-ва 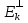 будет ( будет ((х+у,z)=(x,z)+(y,z)=0+0=0и (λх,z)=(xλ,z)=λ(x,z)=0.Т.о. 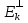 -подпр-во. -подпр-во.Т.Пр-во Еп явл. прямой суммой подпр-во Ек и его ортог. дополнения. Размерность ортог. дополнения к-мерного подпр-ва Ек пр-ва Еп равна п-k. Свойства ортогонального дополнения. 1.( 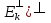 =Ek =EkДок-во.Из опред.ортог.допол.следует,что Ekc( 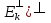 .Пусть Ek≠( .Пусть Ek≠(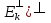 .Тогда существ.z€( .Тогда существ.z€(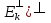 ,но z не принадл.Ek. En=Ek© ,но z не принадл.Ek. En=Ek©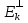 .-->существ.единств.х€ Ek, у€ .-->существ.единств.х€ Ek, у€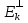 .:z=x+y.Но (z,y)=0,т.к. z€( .:z=x+y.Но (z,y)=0,т.к. z€(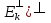 и y€( и y€(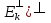 .Но и (х,у)=0, т.к. х€Ek ,y€ .Но и (х,у)=0, т.к. х€Ek ,y€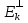 .След-но 0=(z,y)=(x+y,y)=(y,y)Что мб при y=0.Противоречие ч.т.д. .След-но 0=(z,y)=(x+y,y)=(y,y)Что мб при y=0.Противоречие ч.т.д.2.Ek∩ 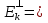 0 03. 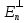 =E0 =E04. 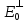 =En =En |

 Лин(в-ное)пр-во.Лин.подпр-во.
Лин(в-ное)пр-во.Лин.подпр-во. 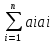 ,тогда
,тогда