Лин(вное)прво. Лин подпрво
 Скачать 446.05 Kb. Скачать 446.05 Kb.
|
|
Собственные числа и собственные векторы квадратной матрицы. Характеристическое уравнение. Пусть А – квадр. матрица. Если сущ-ет вещ. число λ, что ур-ие АХ =λ X имеет ненул. реш-е, где X – в-р-столбец, то число λ наз. собственным знач-ем, а вектор X наз.собственным в-ром матрицы А. Замечая, что X = ЕХ, перепишем дан.ур-ие в виде ур-ния (А -λE )Х = 0, для к-рого по усл. необходимо найти ненул. реш-е.. Допустим опред. квадр. матр. (А -λЕ) отличен от 0. Тогда у неё сущ. обрат. и X = (А-λЕ)-1* 0= 0. Т. е.реше только нулевое. Сл-но собств. в-рам отвечает опред. матр. (А-λЕ)=0. Т. о. для нахождения собств. зн-ний необходимо решить ур-ие |A-λE|=0(от эл-тов глав.диагонали отнимаем λ),которое наз. характеристическим ур-нием - многочлен п-степени по λ( дан. ур-ние имеет не более чем п разл. корней). Т.Собств. вектор, соответствующий дан.собственному зн-нию, определяется с точностью до пост. множителя. Док-во.Пусть X – собств. в-р матр. А , соответствующий собств. зн-нию λ, тогда АХ =λX . Возьмём произвольное вещ. число с≠0 и подействуем матр. А на в-р сХ : А (с Х )= сАХ = сλХ =λ (сХ ). Т.о. сХ - также собств.в-р матр. А с тем же собств. зн-нием. Ч.т.д. Т. Если базисные в-ры явл. собств. в-рами квадр.матр. А, то эта матрица диагональна. Док-во.] баз.в-р ei,i=1,..,n явл. собств.в-рами матр.А.Тогда Aei= 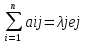 ,где(aji)=A. Откуда aji=δjiλi,т.е. A –это диаг.матр.,имеющая на глав.диагонали эл-ты λ1,λ2,…,λn. ,где(aji)=A. Откуда aji=δjiλi,т.е. A –это диаг.матр.,имеющая на глав.диагонали эл-ты λ1,λ2,…,λn.Т.Если собст.чЧисла λ1,λ2,…,λn, квадр. Матрицы А различны, то отвечающие им собств.в-ры en лин.незав. Линейная функция. Билинейная форма. Квадратичная форма. Ф-ция- это соответствие, при к-ром кажд. эл-ту v пространства V сопостав. только 1 число f(v ). Ф-ция на лин. пр-ве L наз. лин., если для любых в-ров этого пр-ва х, у € L и люб. действ.числа λ€R выпол-ются равен-ва:
Примеры. 1. f : R -> R, f(x) = kх прямая линия на плоскости XOY проходящая через начало коорд. 2., Скаляр. произв. Пусть φ(х,у) числ. Ф-ция, зад. на лин. пр-тве.Если φ(х , у) линейна по кажд. из своих аргументов, то её наз. билинейной формой. Т.о. бил. форма - это ф-ция φ(х, у) зад. на лин. пр-ве L, что при всех x ,y ,z €L и λ€R выполняются рав-ва: 1. φ(х+z,у)=φ(x,у)+φ(z,у),φ(х, у+z )=φ(х,у)+φ(х, z) 2. φ(λх, у) =λφ(х,у);φ(х,λу) =λφ(х,у). Отдельно вводят нул.бил.форму 0(х, у), для к-рой 0(х, у)=0 при всех х,у принад.L. Бил.форма наз.симметричной, если φ(х, у) =φ(у,х)(напр.скал.произв). Если в бил. форме φ(х,у) у = х, то получим квадратичную форму φ(х,х). Квадрат. форма φ(х,х).наз. положительно определённой, если для любого х€ L ,х≠ 0 будет φ(х,х)> 0. В том случае, когда φ(х,х)≥0 квадратичная форма наз. неотриц... Положительно определённые и отриц. опред-ные квадратич. формы наз.знакопостоянными. Изотропный вектор и знакоопределённость квадратичной формы. Матрица квадратичной формы. Закон инерции квадратичных форм. Критерий знакоопределённости квадратичной формы. Ненул. вектор, для к-рого квадратич.форма φ(х ,х)= 0, наз.изотропным. Т. Если квадратич.форма не имеет изотропных в-ров,то она знакопостоянна. Док-во. Предположим, что это не так и найдутся два ненул. в-ра и и υ;, на к-рых квадрат. форма имеет разн.знаки. Т.к. для 2х коллинеарных в-ров х,у существует λ≠0,λ€R, что х=λ у, на к-рых квадратич. форма имеет 1и тот же знак φ(х,х)= φ(λу, λу)=λ2φ(у,у)то в-ры и и v неколлинеарны. Для люб. вещ. числа λ выполняется рав-во φ(u+λυ,u+λυ)=φ(u,u)+λ(φ(υ,u)+φ(u,υ))+λ2φ(υ,υ). Правая часть - многочлен второй степени относительно переменной λ. Т.к. φ(u,u) и φ(υ,υ) по предположению имеют разные знаки, то многочлен имеет 2 корня разн. знака. Пусть λ0 - 1 из них, тогда φ(u+ λ0υ,u+ λ0υ )=0 и и + λ0υ - изотропный в-р. Но в-р и + λ0υне нулевой в силу лин. незав-сти в-ров и и v, поэтому обращение в 0 на нём квадратич. Формы невозможно по усл. Противоречие. чтд. следствие: Знакопостоянство квадратич. формы явл. необходимыми достаточным усл-ем отсутствия изотропных векторов. Матр.А=(aij)=(φ(ei,ej)) наз. матр.квадратич.формы.(матрицей квардатич.формы наз.матрица,составленная из ее коэф.)квадратич.форме соответствует единств.симметрическая матр. Всякую квадратичн.форму можно представить как умножение матриц. Если матрица квадратич. формы диагональна и на диагонали стоят либо +1, либо --1, либо 0, то такой вид квадратичной формы называется нормальным. Для люб. матрицы А квадратич.формы сущ-ет матрица S, что А = S'DS , detS = 1,где D - диагональная матрица. Т.(Закон инерции квадратичной формы.) Число положительных и отриц. членов в нормальном виде квадратич. формы не зависит от способа её приведения. Следствие. Квадратич. форма положительно (отрицательно) определена, когда её положительный (отрицательный)индекс инерции равен размерности пр-ва. Т.(Критерий Сильвестра.) Для того, чтобы квадратич.форма была положительно определена, необходимо и достаточно,чтобы все главные миноры её матрицы были положительны. Т.Д ля того, чтобы квадратичная форма была отрицательно определена, необходимо и достаточно, чтобы знаки главных миноров матрицы квадратичной формы чередовались. Комплексные числа. Формула Эйлера. Решение комплексных неравенств на плоскости. Комплексным числом z наз. упорядоченная пара (x,y) вещественных чисел x и y (или вектор (x,y)). Комплексные числа z1=(x1,y1) и z2=(x2,y2) считаются равными тогда и только тогда, когда x1=x2,y1=y2.Сумма и произведение комплексных чисел z1=(x1,y1) и z2=(x2,y2) определяются равенствами: z1+z2=(x1+x2,y1+y2) z1z2=(x1x2-y1y2,x1y2+x2y1) Люб.компл.число можно записать как z=(x,y)=(x,0)+(0,y)=x+iy. x наз. действительной частью z, y – мнимой частью z. Формула Эйлера связывает комплексную экспоненту с тригонометрическими функциями.Она утверждает, что для любого действительного числа x выполнено следующее равенство:eix=Cosx+iSinx,где е- основание натурального логарифма,i- мнимая единица. Линейные операторы как отображения. Образ и ядро линейного оператора. Пусть V,U-2 лин.пр-ва.Правило по к-рому эл-ту пр-ва v€V сопоставляется единственный эл-т пр-ва u€U наз.отображением. 2 отображения A и B наз.равными,если для люб.v€V будет Av=Bv. Отображение А,действующее из пр-ва V в пр-во U,наз.лин.,если для люб.эл-тов v,v1и v2 пр-ва V и люб.действ.числа λ выполняются след.рав-ва: 1.А(v1+v2)=Av1+Av2 2.A(λv)=λAv Т .множ-во определенных лин.отображений,действующих из пр-ва V в пр-во U,образует лин.пр-во отображений(L(V,U)) Образом отображения А наз.множ-во эл-тов пр-ва U,для к-рых найдется эл-т v из пр-ва V,что Аv=u. Такое множ-во обознач.как ImA.Если образ отображения совпадает со всем пр-вом,то такое отображение наз.наложением или сюръективным. Ядро отображения A наз.множ-во эл-тов v пр-ва V таких что Аv=0(kerA).Отображение,при к-ром разные в-ры имеют разл.образы,наз.вложением или инъективным отображением.Если отображение не инъективно,то его ядро ненул. Отображение явл.инъективным когда его ядро-нул.подпр-во . Взаимно однозначные отображения. Лин.отображение А действует взаимно однозначно из Vв U,если для каж.u€U существ. только 1 v€V.такой что Av=u. Взаимно однозначное отображение явл. одновременно и сюръективным и инъективным,поэтому его ядро нулевое. Если отображение А действует взаимно однозначно из Vв U,то размерноть пр-в V и Uравны. Произведение операторов. Обратный оператор. Пусть лин.отображение B переводит эл-ты лин.пр-ва в V в лин-пр-во U,а лин. отображение Апереводит эл-ты U в лин.пр-во W.Определим произведение отображений А,B как отображение,действующее по правилу ABv=A(Bv).Это лин.отображение переводит эл-ты лин.пр-ва в V в эл-ты лин.пр-ва W.Для люб.v,v1,v2 принад.V и люб.вещ.числаλ. ввиду линейности отображений А и В в пр-вах U и V соответственно, получим 1.АВ(v1+v2)=A(Bv1+Bv2)=ABv1+ABv2 2.AB(λv)=A(Bλv)=A(λBv)=λABv. Также как произведение 2х лин.отображений, можно определить произведение и большего числа отображений: введем лин.отображение С переводящее в-р лин.пр-ва W в в-ры лин.пр-ва H. Произведения лин.отображений удовл.след. св-вам: 1.λ(АВ)=(λА)В Док-во.(λ(АВ))v= λ(АВv)= λ(A(Bv))=( λA)(Bv)=(( λA)B)v. 2.(A’+A’’)B=A’C+A’’B 3.A(B`+B``)=AB`+AB`` 4.(CA)B=C(AB). Рассмотрим такие 2 лин.отображения АВ что А:U-->V и В:VU. Тогда АВ=С:VVт.е.это отображение переводит лин.пр-во в само себя.Такие отображения наз.преобразованиями. Определим единичное образование I как такое,при к-ром для любого эл-та v€V будет Iv=v. Отображение В наз.обратно отображению А,если АВ=I и ВА=Iпротивп.,где I и Iпр.-единичные преобразования в пр-вах V и U соответсвтенно. Если А:VU,то для v€VА-1Аv=v и для u€UAА-1u=u. Если А-1Аv=0,то v=0. Т.для того,чтобы у лин.отображение существ.обратная,необ. и достаточно,чтобы оно было взаимно однозначным.(док-во на стр7,econ2) Матричная запись линейных операторов Т.между матрицами размерности(mxn) и лин.отображениями из лин.пр-ва Vn лин.пр-ва Um во всяких фиксированных базисах пр-в Vn и Um имеется взаимно однозначное соответствие.(док-во на с.8-10,econ2) Т.матрица произведения лин.отображений в заданных базисах равна произведению матриц лин.этих отображений. Система линейных уравнений и ее решение Сист. m лин.равнений с n неизвестн-это сист.ур-й вида a11x1+a12x2+…+a1nxn=b1 a21x1+a22x2+…+a2nxn=b2 am1x1+am2x2+…+amnxn=bm m-кол-во ур-й, n-количество неизвест.. x1, x2, …, xn –неизвест., к-рые надо определить. a11, a12, …, amn-коэф.сист. ,b1, b2, … bm –своб.члены- предполаг.известн.Индексы коэф.(aij) сист. обознач. номера ур-я(i)и неизвест.(j), при к-ром стоит этот коэф. Реш-м сист. лин. ур-й наз.упоряд.совокуп.чисел.( 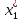 , ,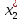 ,…, ,…,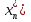 =x*, при подстан.к-рыx вместо неизв.(x1,x2,…xn)= х каждое ур-е сист. станов. верным числ.рав-вом. =x*, при подстан.к-рыx вместо неизв.(x1,x2,…xn)= х каждое ур-е сист. станов. верным числ.рав-вом.Сис.ур-й наз.совмест.,если она имеет хотя бы 1реш-е. Иначе сист.наз. несовмест. Совмес.сист.наз.опред.,если она имеет единств.реш-е. Иначе сист.наз.неопред. Сист.ур-й наз.однород.,если все её своб.члены =0. Т. Сис.однор.ур-й всегда имеет реш-е. Док-во. Можно указать это реш-е. Это тривиал.реш-е х = (0,0,... ,0).чтд. Т.о. в случае однор.ур-й одно реш-е есть всегда. Для нахождения всех реш-й произвол. сист. ур-й потребуется преобраз.исходную сист. Теорема об элементарных преобразованиях системы линейных уравнений. Метод Гаусса для решений совместной системы линейных уравнений. Т. Любая сист.лин.ур-й с помощью элемент.преобр.и изменением нумерации неизвестных мб приведена к сист.с трапециевидной матр. Преобр-я ур-й, при к-рых сохр.реш-я, наз.эквивал., а сами ур-я равносил.Для сист.лин.ур-й эквивал.будут след.преобр-я: 1) к ур-м сист. можно прибавлять др. ур-я сист. 2) ур-я сист. можно умнож. на ненул.числа, 3) изменение порядка следования строк ур-й 4) в ур-х сист.можно менять порядок следования перем.(в этом случае по договорённости меняют порядок следования перем.во всех ур-х сист. по одному правилу) 5) если в сист.ур-й имеется две пропорц.строки,то одну из них можно вычеркнуть. Преобр-я 1-2 наз. лин., а метод реш-я сист.лин.ур-й, основан.на преобр-х 1-5-мет.Гаусса.Вместо многократ.перепис.сист.ур-й испол.сокр. запись в виде матриц.
Теорема о числе решений совместной системы линейных уравнений. Если сист. лин.ур-й имеет 2 разл.реш-я, то она имеет бескон.много реш-й. Док-во. ] сист.имеет 2 разл.реш-я x1,x2. Покажем, что при любом вещ. C реш-е также будет xc=Сx1+(1-C)x2, при этом хс≠х1, хс≠х2, когда С≠{0;1}.Используя матр.форму записи сист.лин.ур-й, получим: Ахс=А(Сх1+(1-С)х2)=CAx1+(1-C)Ax2=Cb+(1-C)b=b. Т.к. число С-любое, то кол-во реш-й бескон.много.чтд. Решение квадратной системы линейных уравнений с помощью обратной матрицы. Если в сист.лин.ур-й число неизв.=числу строк, то осн.матр.этой сист.-квадр.Известно, что когда ранг квадр.матрицы= числу ее строк, то у матр.коэф-тов.сист. имеется обр.матр. сист.имеет единств.реш-е X = А-1В. Формулы Крамера. ] задана сист.лин.ур-й с равным кол-вом неизвест. и свобод.членов. Т. Если определ.коэф.при неизвестных |А|= ∆(А) квадр.сист.лин.ур-й ≠0,то её реш-е имеет вид: xi = 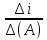 , где i=1,2,…,n и где ∆i-опред.сист., получающийся заменой столбца матр.коэф-в при неизвестной xiстолбцом свободн.членов. , где i=1,2,…,n и где ∆i-опред.сист., получающийся заменой столбца матр.коэф-в при неизвестной xiстолбцом свободн.членов.Док-во. Домножим 1-ю строку сист.на А11-алгебр.доп. эл-та а11, 2-ю- на А21 и т.д., посл.строку на An1. Сложим все левые части и соотв-но все правые части сист..В рез-те получим: х1(a11A11+a21A21+…+an1An1)+x2(a12A11+a21A21+…+an2An1)+…+xn(a1nA11+a2nA21+…+annAn1)=b1A11+b11A11+…+b11A11. Для опред.выр-я в скобках при неизветст.х2 ,х3,…,хn=0 можно написать ∆(А)х1=∆1, т.к. опр-ль ∆(А)≠0,то х1= 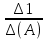 . Теперь домножим 1-ю строку сист.на А12, 2-ю на А22 и т.д., посл-на А22 и все сложим. После упрощ-я получим х2= . Теперь домножим 1-ю строку сист.на А12, 2-ю на А22 и т.д., посл-на А22 и все сложим. После упрощ-я получим х2=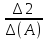 . Повторим указан.процедуру для перем.х3,…,хn.чтд. . Повторим указан.процедуру для перем.х3,…,хn.чтд.Матрицы и их классификация. Действия с матрицами. Экономические примеры. ] имеется табл.эл-ов,содерж.m-строк и n-столбцов: 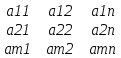 Матрицей размера mxn называется прямоугол.табл.чисел, обозначаемая как А=(аij), где i-m-строк, j-n-столбцов. Матрицей размера mxn называется прямоугол.табл.чисел, обозначаемая как А=(аij), где i-m-строк, j-n-столбцов. Над матр.определены след.операции: 1.Умножение на число, когда на число умножаются все эл-ты матр. k(aij)=(kaij). 2.Если матрицы имеют одинаковое число строк и столбцов, то при сложении матрицы складываются как соотв.эл-ты: (аij)+(bij)=(aij+bij). 3. Если число столбцов матр. аij равно числу строк матр.(bij),то при умножении матрицы А на матр.B получается матр. С(ij), эл-ты к-рой сij равны аi1b1j+ai2b2j+…+ainbnj(умн-е строки на столбец). *Две матр.наз. равными, если их соотв.эл-ты равны. *Нулевой матр.наз.матр., состоящ.из одних нулей *Матрицей противоположной матрице А, наз.матр. вида -1А=-А Классификация матр. 1.Матр., у к-рой все эл-ты выше(ниже) главной диагонали равны 0, наз. нижнетреугольной(верхнетреугольной) или просто треугольной. 2.Матр., у к-рой число строк и столбцов равное наз.квадратной. 3. Квадр.матр., у к-рой все эл-ты, кроме главной диаг.нули, наз.диагонал. 4. Диагонал.матр., у к-рой все эл-ты главн.диаг.равны м/у собой, наз. скалярной матр. 5. Скалярн.матр., у к-рой все эл-ты главн.диаг. равны 1, наз. единичной(Е). 6.Матр. 1хn- вектор-строка и матр. nx1-вектор-столбец. Если у матр.поменять местами строки и столбцы, то такая матр.называется транспонированной. |

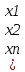 ) , b=
) , b=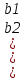 ), A=
), A=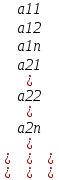 )
)