Лин(вное)прво. Лин подпрво
 Скачать 446.05 Kb. Скачать 446.05 Kb.
|
|
Эллипс. Каноническое уравнение эллипса и его свойства. Эллипсом называется множество всех точек плоскости , сумма расстояний от каждой из которой до двух данных точек этой плоскости , называемых фокусами, есть величина постоянная , большая ,чем расстояние между фокусами MF1+MF2=2a MF1= 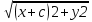 МF2= МF2=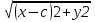 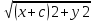 + +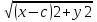 =2a =2aканоническое уравнение эллипса: Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Эллипс-кривая второго порядка. Св=ва Если a=b,ТО ЭЛ.ПРЕВРАЩ. в окр-ть Если для М(х1у1)вып усл Х12/а2+у12/b2<1,то точка находится внутри элп,если >1 то снаружи С фигурой эл.связаны 2 прямые,наз.директрисами х=а/е х=-а/е Парабола. Каноническое уравнение параболы и его свойства. Параболой называется геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы). Каноническое уравнение параболы в прямоугольной системе координат: У2=2px Гипербола. Каноническое уравнение гиперболы и его свойства.  Вектор- называется всякая величина, обладающая направлением. Вектор, началом которого служит точка А, а концом точка- В, обозначается АВ. Длина вектора, также называется модулем. Модуль это скалярная величина, обозначается двумя вертикальными чертами. Нуль-вектор- это вектор длина которого равна 0. Равенство векторов- два(ненулевых)вектора а и b равны, если они равнонаправленные и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны. Вектор можно переносить параллельно самому себе , а начало вектора помещать в любую точку О пространства. Равные векторы так же называют свободными. Коллинеарные – векторы а иb называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают, а||b. Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору. Компланарные- три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов, хотя бы один нулевой или два любые коллинеарные, то такие векторы компланарны. Орт вектор- вектор, длина которого равна единице, называется единичным вектором и обозначается через ē. Единичный вектор, направление которого совпадает с направлением вектора а, называется ортом вектора а и обозначается а°. Действия с геометрическими векторами в координатной форме. признак коллинеарности векторов. 1) при сложении векторов их координаты складываются, т.е если а=а1+а2, то Х=х1+х2, У=у1+у2, z=z1+z2 2) аналогичное правило для вычитания векторов 3) При умножении вектора на число все координаты умножаются на то же число 4) такое же правило и для деления вектора на число. А так же: Каждый вектор равен сумме его геометрических проекций по трем осям координат. .Скалярное произведение геометрических векторов и его свойства. Признак ортогональности векторов. Скалярным произведением двух ненулевых векторов а и bназывается число , равное произведению длин этих векторов на косинус угла между ними. а *b= |a|*|b|*cosa. формуле можно придать иной вид, так как|а|*cosa= проекция а на b, а |b|*cosa= проекция b на а. получаем: а*b=|а|* проекция b на а= |b|* проекция а на b, т.е скалярное произведение двух векторов равно модулю одного из них , умноженному на проекцию другого на ось, со направленную с первым вектором . Свойства скалярного произведения:
Признак ортогональности векторов. Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е. .90 градусов Векторное произведение: определение ,вычисление и свойства. Три некомпланарных вектора a,bи с, в указанном порядке образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму совершается против часовой стрелки, и левую если по часовой. Векторным произведением вектора а на вектор b называется вектор с, который:
Векторное произведение обозначается а *b Из определения векторного произведения вытекает следующее соотношение между ортами I,j,k: i*j=k, j*k=I, k*i=j. Свойства векторного произведения: |
