кп. Литература Приложение
 Скачать 0.64 Mb.
|
|
Расчёт координаты середины поля допуска, корректирующего звена по формуле:  Расчёт предельных отклонений корректирующего звена:  ; .Решение проверочной задачи способом сложения и вычитания номинального размера и предельных отклонений.  Подготовим уравнение для сложения и вычитания:  6.5 Расчёт подетальной размерной цепи вероятностным методом. Проектная задача Метод расчёта – вероятностный, способ – одинакового квалитета  .Расчёт количества единиц допуска: 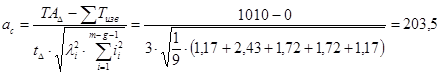 Назначаем квалитет по таблице П.7.2 в зависимости от стандартного  , ближайшего к расчётному . Принимаем 13-й квалитет.Допуски звеньев  устанавливаем по 13-му квалитету, а допуск звена по 14-му квалитету. Допуски записаны в таблице 6.4.Расчёт допуска корректирующего звена из условия следующей формулы:  , тогда , откуда .Назначение предельных составляющих звеньев:  Расчёт координаты середины поля допуска:  Расчёт предельных отклонений корректирующего звена;  ; .Допуск замыкающего звена:  Координата середины поля допуска:   Предельные отклонения замыкающего звена:   Таблица 6.4 Сведения о размерной цепи, рассчитанной теоретико-вероятностным методом
Заключение Сравнение допусков (табл.6.3 и табл.6.4) на изготовление составляющих звеньев одной и той же размерной цепи показывает, что величину допуска можно рассчитать в 1,6-2,6 раза точней, если распределение погрешностей изготовления подчиняется закону нормального распределения. 6.6 Замена размеров в размерной цепи Исходные данные: 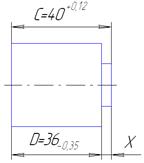 Рисунок 6.6 Первый вариант замены. Вместо размера С указать на чертеже размер X: Запишем уравнение расчёта и подставим в него предельные значения размеров C и D.  ;  , откуда ;  , т.е.  Это указывает на то, что замена размера С размером X без уменьшения допуска размера С невозможна рисунок 6.7. 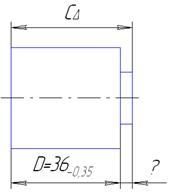 Рисунок 6.7 Второй вариант замены. Вместо размера D указать на чертеже размер X: Запишем уравнение  ;  . ;  , откуда ;  ,Следовательно  Схема замены показана на рисунке 6.8. 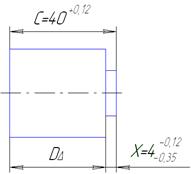 Рисунок 6.8 Сумма допусков размеров D и X после замены должна быть равна допуску заменяемого размера  мм. Поверхность I получают, как правило, чистовым точением. Поэтому обеспечить точность размеров D и X с суммарным допуском 0,3мм практически возможно.7. Зубчатые передачи Исходные данные: Обозначение точности колеса: 10 – 8 – 6 – А. Модуль:  .Число зубьев:  Коэффициент смещения исходного контура колеса:  .Расшифруем условное обозначение передачи: 10 – 8 – 6 – А 10 – степень точности по норме кинематической точности; 8 – степень точности по норме плавности работы; 6 – степень точности по норме контакта зубьев; А – вид сопряжения, ограничивающего боковой зазор. Так как вид допуска на боковой зазор не указан, то он совпадает с видом сопряжения, то есть, обозначен символом “А”. Устанавливаем комплекс контроля по ГОСТ 1643-81 Выписываем нормируемые погрешности:  - наибольшая кинематическая погрешность зубчатого колеса (по норме кинематической точности), - местная кинематическая погрешность (по норме плавности работы), - погрешность направления зуба (по норме контакта), - наименьшее отклонение толщины зуба и допуск на толщину зуба (по норме бокового зазора).Назначаем допуски на погрешности: Допуск определи по следующей формуле  где:  - допуск на накопленную погрешность зубчатого колеса- допуск на погрешность профиля зуба колеса  ;  ;  Допуск - определяем в зависимости от степени точности по норме плавности – 8, модуля m=4мм, делительного диаметра  : Допуск  определяем с учётом степени точности по норме контакта – 6, модуля m=4мм, ширины венца  где:  - коэффициент ширины зуба колеса, для цилиндрических прямозубых колёсПринимаем |
