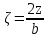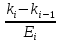Лекции по Механике грунтов. Литература сниП 02. 0183. Основания зданий и сооружений сниП 02. 0385. Свайные фундаменты
 Скачать 7.74 Mb. Скачать 7.74 Mb.
|
|
Пример. Рассчитать осадки фундамента под колонной. Nн =1130кН, d=1,65м, b=2,1м, l=3м, Р0=0,201МПа. 1 слой – суглинок: Е=19МПа и мощность этого слоя 5,01м 2 слой – песок мелкий: Е=14МПа Рис 10.2 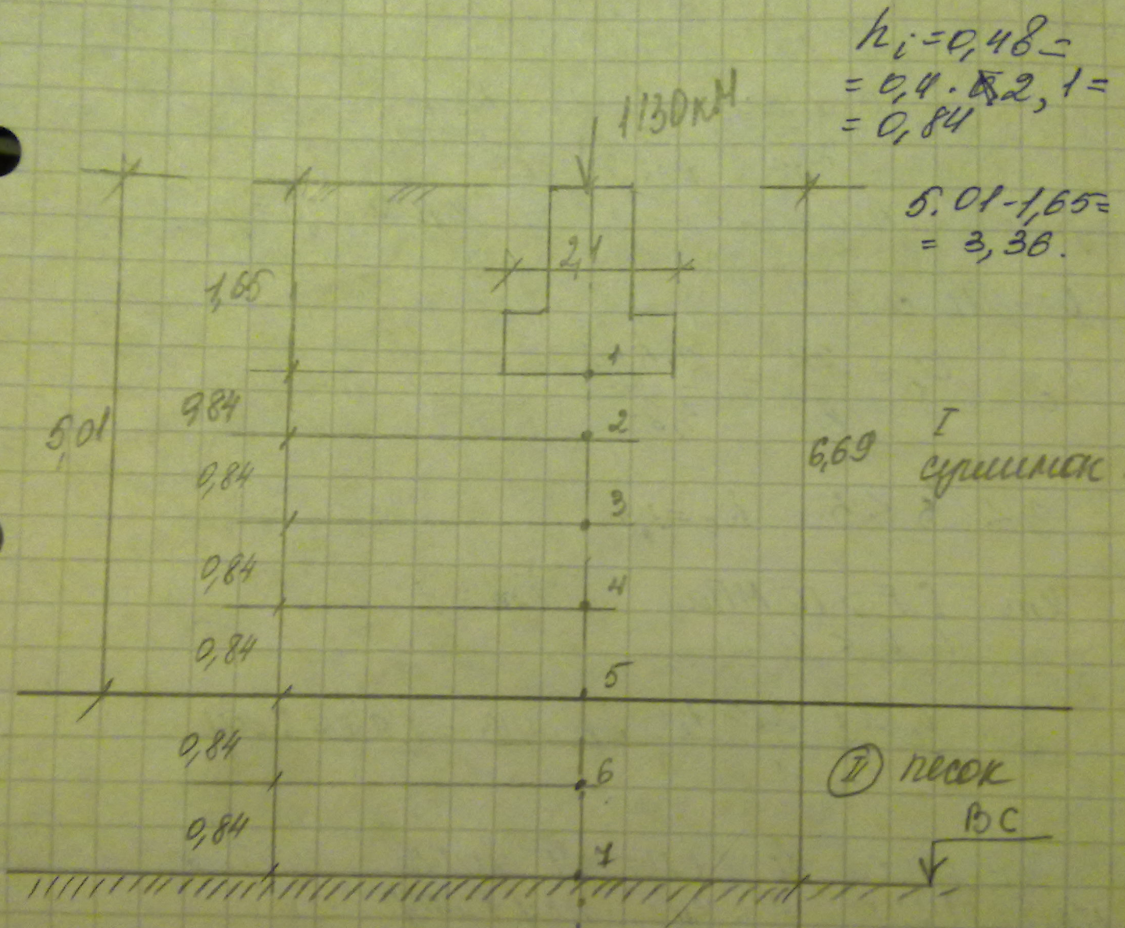 На границе слоев определяются коэффициенты ki и расчеты все сводятся в таблицу.
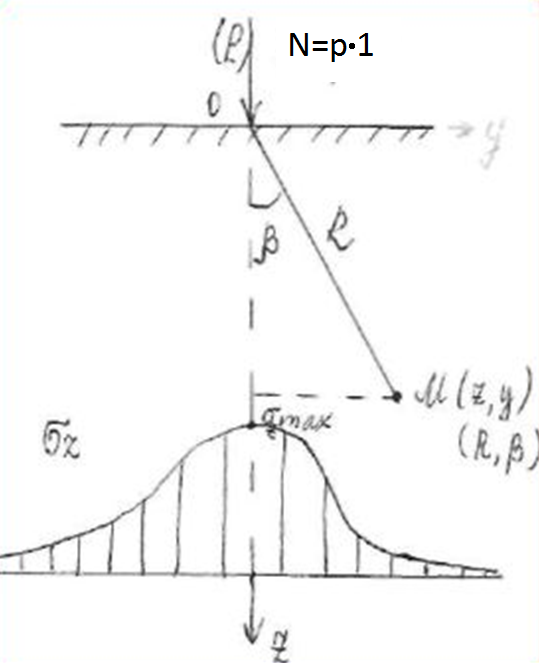
Лекция 11 – 06.12.11 Осадка основания с использованием расчетной схемой линейно-деформируемого слоя или слоя конечной толщины определяется по формуле: 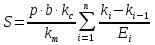 Для фундаментов шириной b<10м Р=Р0. Р0=0,201МПа b=210м 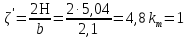 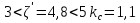 b<10м, Р>10МПа. 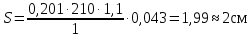 Проверка по второй группе предельных состояний S≤Su [прил 4 стр 38] Su=8см (пром,ж/б) Su=10см (кирпичн) Su=20см (кирпичн+лент ф) 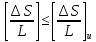 S – разность между осадками соседних фундаментов 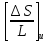 - предельно допустимое значение относительной неравномерности осадок (по СНиП) - предельно допустимое значение относительной неравномерности осадок (по СНиП)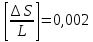 - для колонны с ж/б каркасом - для колонны с ж/б каркасомРис 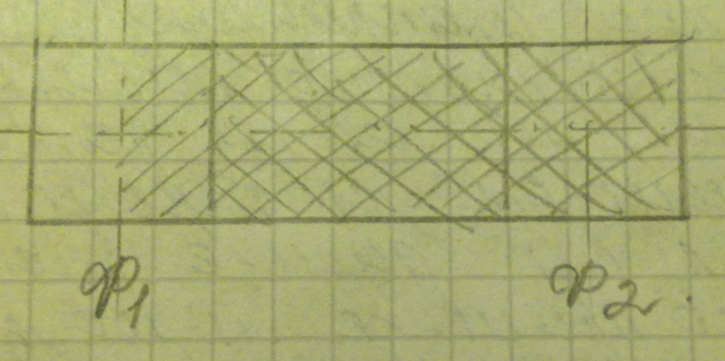 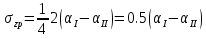 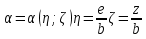 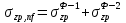 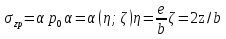 Рис 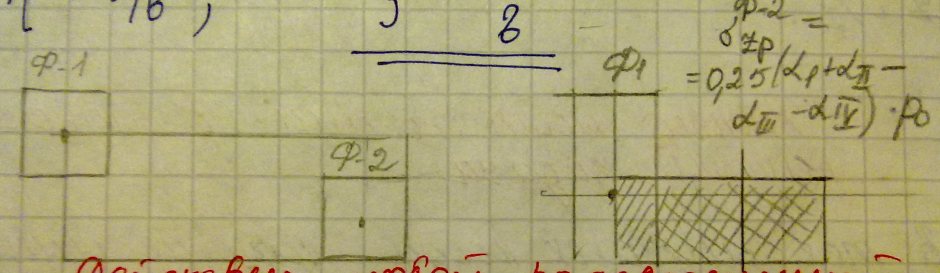 Действие любой распределенной нагрузки 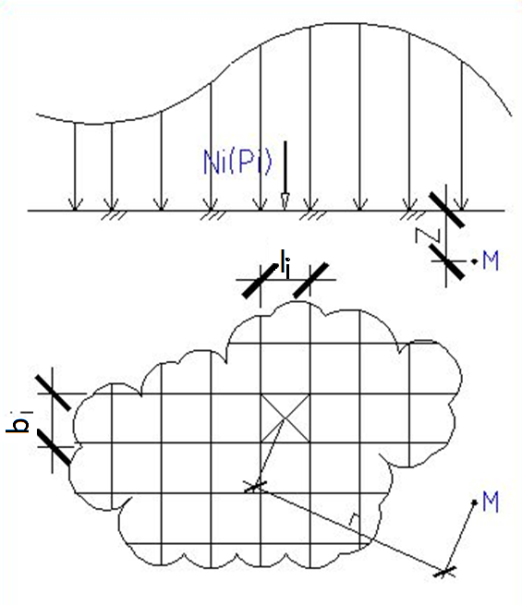 Пусть к поверхности изотропного линейно-деформируемого пространства приложено распределенное давление загруженную плоскость можно разбить на небольшие прямойгольники со сторонами pi*bi с некоторым приближением давление распределяется в пределах i-ого прямоугольника можно заменить равнодействующей Ni (Pi), приложенной в центре тяжести, тогда σzp 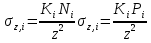 Определив величину σzp каждого прямоугольника и произведя суммирование напряжений по всей пл-ти опред σz от действия местной распределенной нагрузки 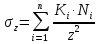 где Кi– табличный коэффициент, зависящий от ri/z. Распределение напряжений в случае плоской задачи В тех случаях, когда сооружение имеет большую дляну l, по сравнению с шириной b. Их часто рассматривают в условиях плоской деформации. Условия плоской задачи будет иметь место в тех случаях, когда направление распределено в одной плоскости, а в перпендикулярном напрвлении они либо =0, либо постоянны это х-но для вытянутых в плане сооружений (например ленточных фундаментов, подпорочных стен, насыпей, дамб…). Если l/b≥10 – услоавие плоской деформации. 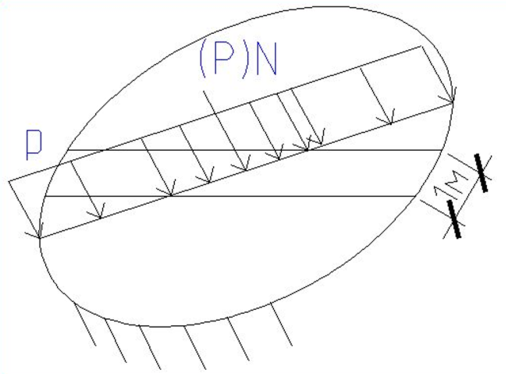 Если ширина по сравнению с длиной мала, то расчетная схема может быть принята в виде линейной нагрузки. Если мы не должны пренебрегать шириной по сравнению с длиной, то рассматривается полосовая нагрузка.
 Впервые решение такой задачи получено Фламаном. Он рассматривал линейно-деф-ю однородность и изотропную полуплоскость. 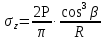 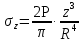 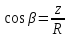
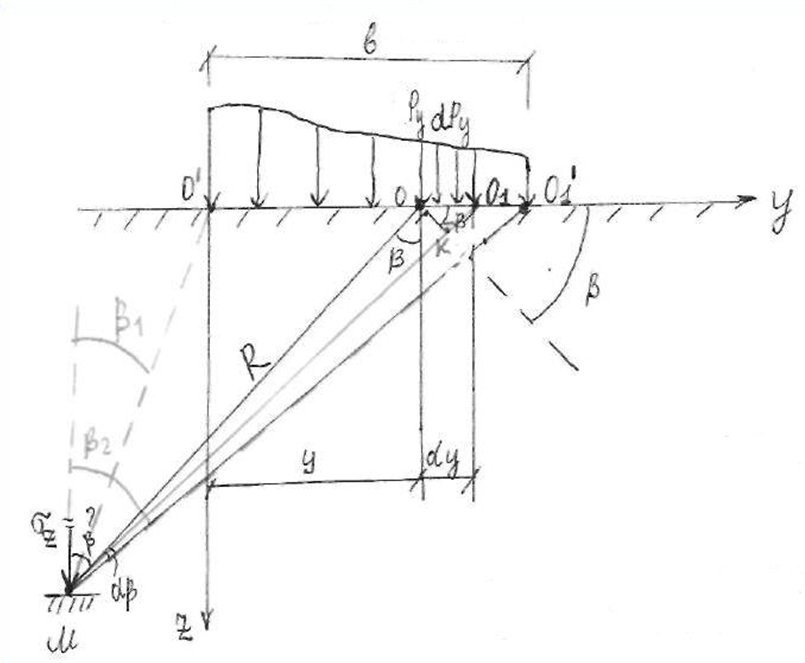 dPy – интенсивность нагрузки, приходящаяся на бесконечно малый элемент нагруженного участка dPy = Py ∙ dy Применим формулу Фламана: 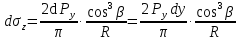 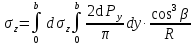 В этой формуле имеются три переменные: y, β, R - их нужно свести к одной. Из точки М проведем радиус в точку 01. Из точки 0 опустим перпендикуляр на МО1. Ð ОКО1 = 900 ОК = R ∙ dβ OK = 001 ∙ cosβ 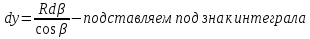 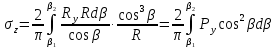 От β1 до β2 от начала до конца изменения β. Лекция 12 – 16.12.11 При Py = P = const 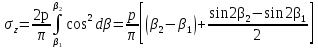 Главные напряжения Можно найти величину и направление главных напряжений: 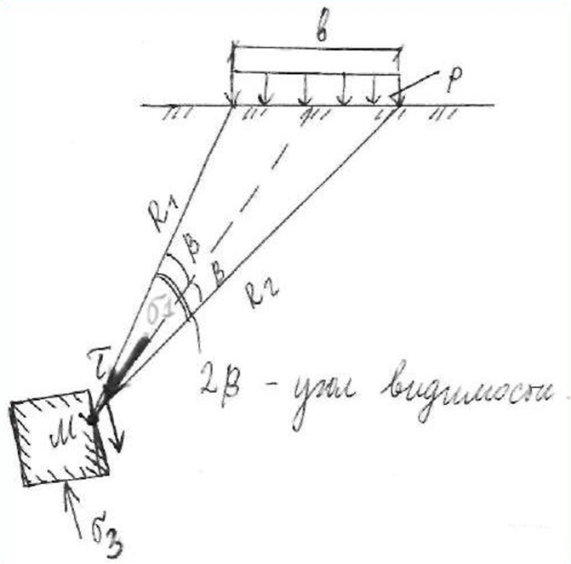 Наибольшие главные напряжения σ1 направлено по биссектрисе угла видимости. σ3 наименьшее главное напряжение. σ2 действует перпендикулярно плоскости тетради. 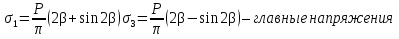 Напряжения от действия собственного веса грунта 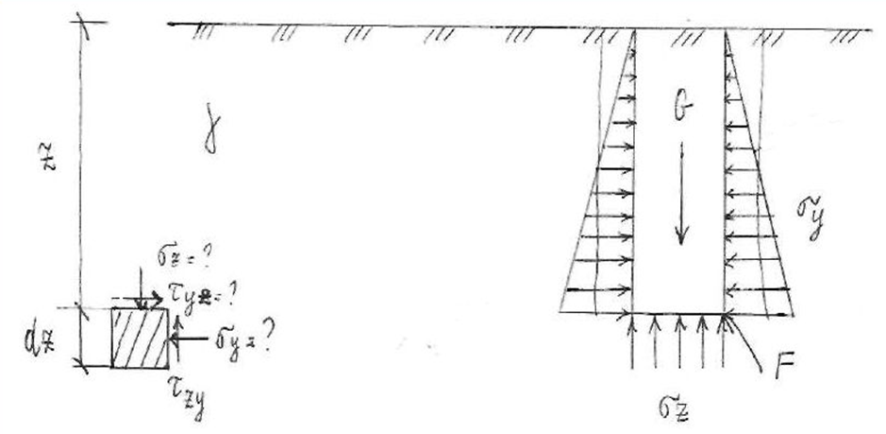 Применим метод сечений. τyz = - τyz = 0, т.к. 2 цилиндра не могут смещаться относительно друг друга, трения нет. Остаются только нормальные напряжения ∑Z = 0 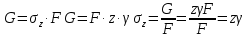 С глубиной напряжения в однородном грунте возрастают линейно (эпюра треугольная). Боковое расширение невозможно, так как грунт находится в условиях компрессионного сжатия. sy = x ∙ sz «x » - коэффициент бокового давления грунта, при невозможности его бокового расширения. sz = s1 sy = sx = s3 = s2 x выражается через табличный коэф-т Пуассона «ν» (коэф-т бокового расширения грунта). 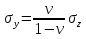 Эти выражения получены для однородного грунта, а если грунт будет слоистый, то: 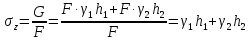 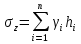 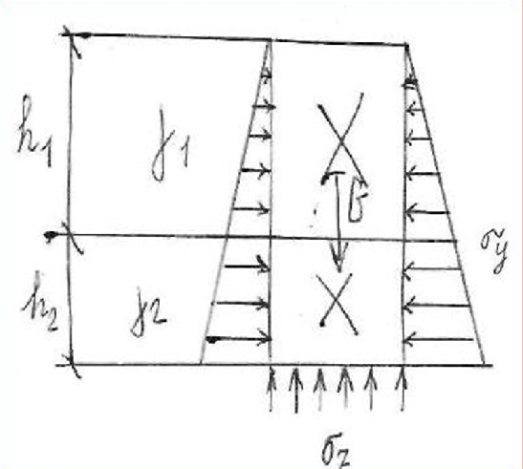 Распределение давлений по подошве сооружений, опирающихся на грунт (контактная задача) - Самостоятельно Фазы напряженного состояния грунта Предельное напряженное состояние грунта в данной точке соответствует такому напряженному состоянию, при котором малейшее добавочное силовое воздействие нарушает существующее равновесие и приводит грунт в неустойчивое состояние: в массиве грунта возникают поверхности скольжения, разрывы, просадки и нарушается прочность между его частицами и их агрегатами. Такое напряженное состояние грунтов следует рассматривать как совершенно недопустимое при воздействии на них сооружений. Поэтому для инженерной практики важно уметь оценить максимальную возможную нагрузку на грунт, при которой он еще будет находиться в равновесии, то есть не будет терять прочность и устойчивость. Пусть на поверхность грунта через жесткий штамп огранич-х р-ров передается нагрузка и все время производится наблюдение за осадками штампа. Приведем характерную кривую деформации грунта от действия на его поверхность местной возр-ей ступенями нагрузки. 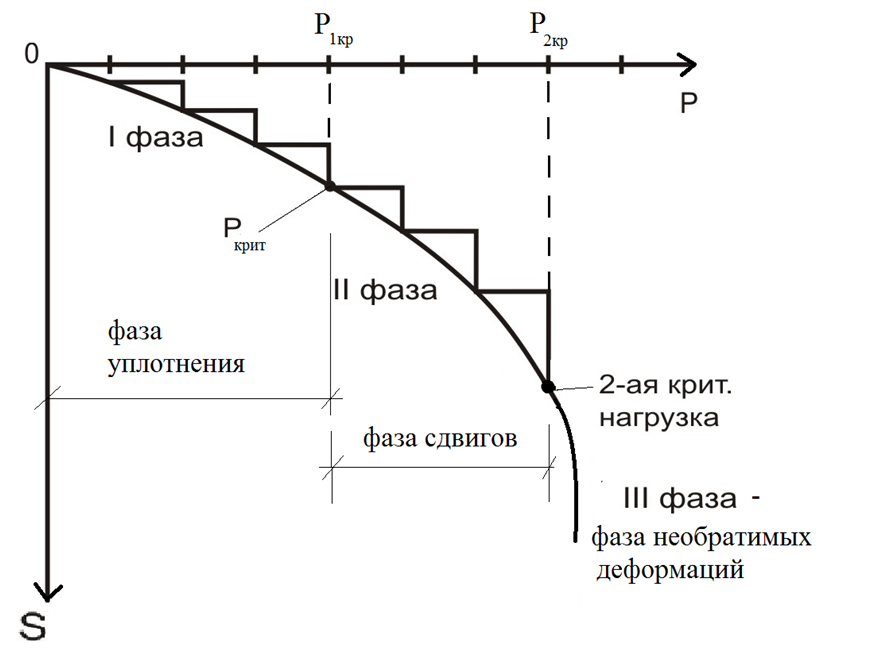 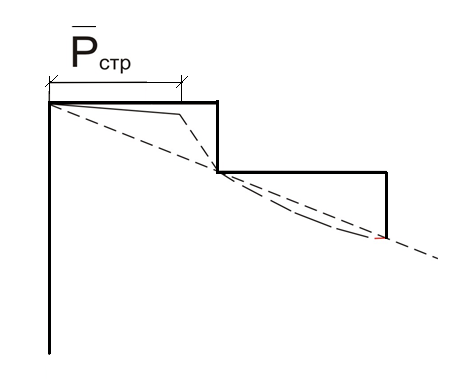 Если ступени нагружения малы и грунт обладает связностью, то первые участки на кривой деформаций будут почти горизонтальны, то есть пока не превышена структурная прочн-ть грунт будет испытывать только незначительные упругие деформации и осадка штампа будет полностью вост-ся при разгрузке. При последующих ступенях нагружения или даже при первой, когда будет превышена структурная прочность грунта возникает уплотнение грунта под нагрузкой, то есть уменьшается пористость грунта в некоторой его области, под нагружаемой поверхностью. Первая фаза напряженного состояния называется фазой уплотнения. В строительстве такое состояние грунта будет полезным, так как грунт в фазе уплотнения приобретает более плотную структуру и будет давать меньшие осадки. При уплотнении зависимость между общими деформациями и давлением (сжимающим напряжением) с достаточной для практических целей точностью мажет быть принята линейной. Улотнение грунта под нагрузкой может продолжаться еще при нескольких степенях нагрузки. Но при достижении его некоторой величины возникает все больше скольжений сдвигов (между частицами грунта, так как в отдельных местах сопротивление сдвигу преодолевается и скольжение между частицами постепенно формируется в отдельной площадке скольжения и зоны сдвигов). Конец фазы уплотнения и начало образования зон сдвигов соответствует начальной критической нагрузке (или 1-ой критической нагрузке). 1ая критическая нагрузка – нагрузка, соответствующая началу возникновения в грунте зон сдвигов и окончанию фазы уплотнения, когда под краем нагрузки между касательными и нормальным напряжениями возникают соотношения, приводящие грунт (сначала у ребер подошвы фундаментов) в предельное напряженное состояние [ПНС]. 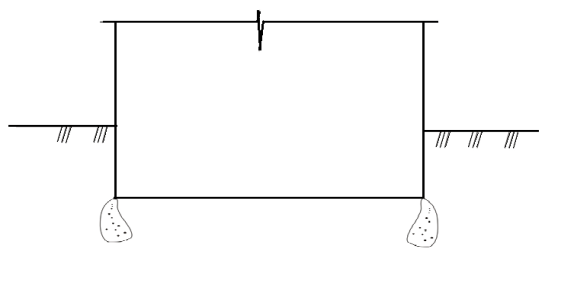 В конце фазы уплотнения (начале фазы сдвигов) непосредственно под штампом начинает формироваться жесткое ядро ограниченных смещений частиц, которое в дальнейшем расклинивает и разжимает грунт в стороны, обуславливая значительные осадки штампа. Ядро полностью сформировывается при достижении грунтом его максимальной несущей способности, после чего остается неизменным, но возникают добавочные пластические области ядра, которые меняя свое положение, выискивают более слабые места в массиве грунта, в то время как жесткое ядро, оставаясь без изменения, внедряется в массив грунта. При возникающем при этом предельным напряженным состоянии грунта преобладают боковые смещения частиц и формируются непрерывные поверхности скольжения, в результате чего толща грунта теряет устойчивость. При дальнейшем увеличении нагрузки наступает вторая фаза - фаза сдвигов. 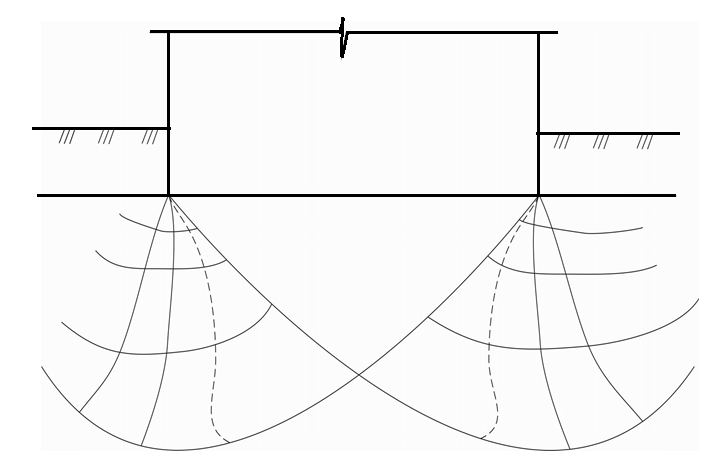 2ая критическая нагрузка – нагрузка, при которой под нагруженной поверхностью сформировываются сплошные области предельного равновесия, грунт приходит в неустойчивое состояние и полностью исчерпывается его несущая способность. 3 фаза –фаза необратимой деформации(пластическое или прогрессирующее течение, выпирание, просадка и др. недопустимых деформаций основания). Предельное напряженное состояние в точке для сыпучих и связных грунтов При действии на поверхности грунта в любой точке М для любой площадки mn проведенную через эту точку под углом α возникнут нормальные касательные напряжения. К нормальным напряжениям следует относить и силы связности, суммарно оценивающие давление связности ре . Тогда на mn будут действовать нормальные напряжения σα+ре и касательные τα 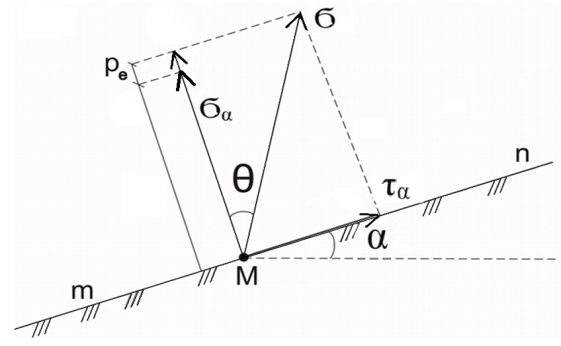 При изменении угла α величины составляющих напряжений, так же будут меняться и если касательные (сдвигающие напряжения) достигнут определенной доли от нормальных, то как показывают опыты на сдвиг произойдет скольжение одной части грунта относительно другой. Таким образом, условием предельного равновесия грунта в данной точке будет: 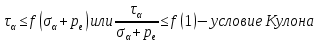 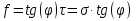 Если f - величина постоянная, то в предельном состоянии она представляет собой тангенс угла наклона прямолинейной огибающей кругов предельных напряжений, кругов Мора. Рис 1. Для сыпучих грунтов: 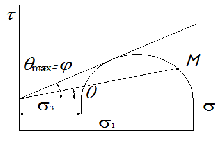 Для связных грунтов: 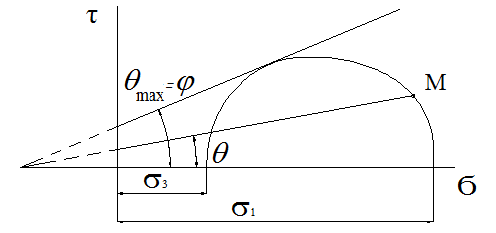 С другой стороны согласно рис 1 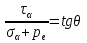 Это отношение равно тангенсу угла отклонения θ, т.е. угла, на который отклоняется полное напряжение для площадки τ от нормали к этой площадке. Т.к. через заданную точку можно провести множество площадок, то, очевидно, необходимо отыскать самую невыгодную площадку, для которой будет существовать максимальный угол отклонения θmax, тогда tg(θmax)≤f. 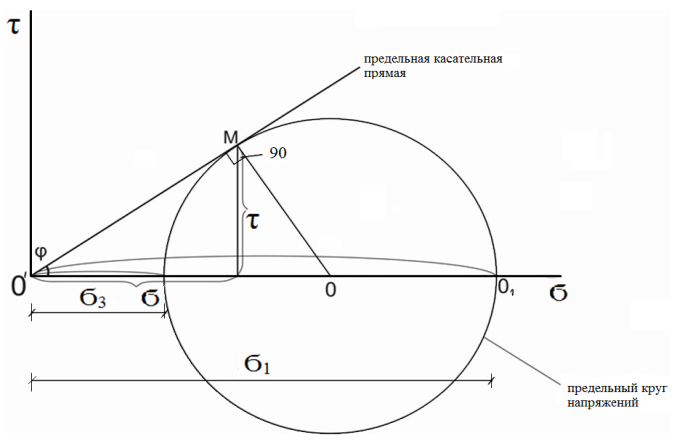 OO1=r (радиус круга мера) 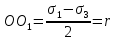 Рассмотрим ∆O'MO: 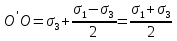 OM=OO1=r 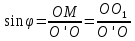 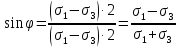 – условие Мора – условие предельного равновесия для сыпучих грунтов. – условие Мора – условие предельного равновесия для сыпучих грунтов.Ему можно придать другой вид после несложных тригонометрических преобразований, а именно: 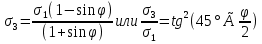 Это выражение широко используются в теории давления грунтов на ограждение. Знак «-» соответствует активному давлению, а «+» пассивному сопротивлению сыпучих грунтов. Условию предельного равновесия можно придать другой вид, выразив главные напряжения σ1 и σ3 через составляющие напряжений σz , σy , τ zy .  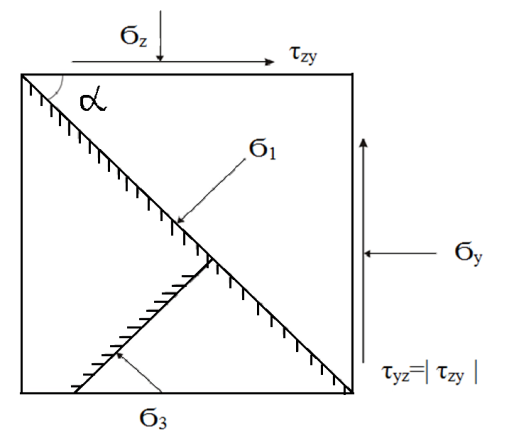 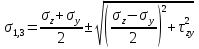 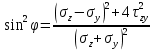 Для связного грунта: 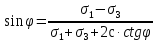 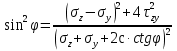 Расчет оснований по несущей способности. (по I группе предельных состояний) F≤γc*Fu/γn , где F - расчетная нагрузка Fu- сила предельного состояния (сопротивление основание) γn– коэффициент надежности, принимаемый в зависимости от класса зданий (1,1-1,2) γc - коэффициент условия работы, принимаемый в зависимости от вида грунта. Расчет по I группе предельных состояний производится в следующих случаях:
|