ТОО «КОЛЛЕДЖ ЕСЕНОВА»
«Согласовано» «Утверждаю»
Методист: Зам.директора по УР
____________ Рисбаева Р.Б. ____________ Кадирханова Р. К.
«______»_______ 2020 г. «______»_______ 2020 г.
Открытый урок
Предмет: Математика
Тема: «Логарифм числа и его свойства»
Специальность:0111000 Основное среднее образование
Курс: І
Группа: ОСО-20
Подготовила: Сактаганова А.Ж.
Актау 2020г.
Раздел долгосрочного плана: 11.3В Показательная и логарифмическая функции
|
ТОО «КОЛЛЕДЖ ЕСЕНОВА»
|
Дата: 19. 11. 2020 г.
|
ФИО преподавателя: Сактаганова А.Ж.
|
Группа: ОСО-20
|
Количество присутствующих: 19
|
отсутствующих: нет
|
Тема урока
|
Логарифм числа и его свойства.
|
Вид урока
|
Изучение новой темы
|
Цели обучения, которые достигаются на данном уроке
|
11.4.1.16 знать определения логарифма числа, десятичного и натурального логарифмов.
|
Цели урока
|
Знает понятие логарифма, его виды и умеет его вычислять.
|
Критерии оценивания
|
Студент достиг цели, если:
- знает понятие логарифма, связывает его с понятием степени, её основанием и показателем;
- вычисляет логарифмы чисел по разным основаниям;
- знает основание десятичного логарифма, умеет его записывать и вычислять;
- знает основание натурального логарифма, умеет его записывать и вычислять.
|
Языковые цели
|
Студенты будут:
- использовать предметную лексику и терминологию раздела при решении задач;
- комментировать ход решения задач.
Лексика и терминология, специфичная для предмета:
- логарифм;
- логарифм числа;
- основание логарифма;
- десятичный логарифм;
- натуральный логарифм;
- подлогарифмическое выражение;
- логарифмическое выражение.
Полезные выражения для диалогов и письма:
- logab читаем: «логарифм по основанию а от числа b или логарифм числа b по основанию а»;
- lg a читаем: «десятичный логарифм числа а»;
- ln a читаем: «натуральный логарифм числа а»;
- значение log231 меньше числа 5, так как ….
|
Меж-предметные связи
|
Физика, астрономия, информатика (через развитие общих ключевых навыков).
|
Навыки использования ИКТ
|
Использование возможностей интерактивной доски.
|
Предварительные знания
|
Знание и применение понятия степени и ее свойств, корня п-й степени и его свойств.
|
Ход урока
|
Запланиро-ванные этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Начало урока
1-3 мин
|
Определение целей и темы урока
Преподаватель:
- Как называется запись 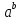 ? / ожидаемый ответ: степень. ? / ожидаемый ответ: степень.
- Как при этом называют a? / ожидаемый ответ: основание степени.
- Как при этом называют b? / ожидаемый ответ: показатель степени.
- Вычислите 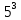 . / ожидаемый ответ: 125. . / ожидаемый ответ: 125.
- Определите, какой показатель должен быть у степени, в которую надо возвести основание 3, чтобы получить 81. / ожидаемый ответ: 4.
- Если обозначим искомый показатель переменной х, то можем записать уравнение 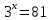 . Действие, по средствам которого находится показатель х степени по значению степени 81 и основанию 3, называется нахождением логарифма. . Действие, по средствам которого находится показатель х степени по значению степени 81 и основанию 3, называется нахождением логарифма.
- Итак, цель нашего сегодняшнего урока: знать определение логарифма числа, десятичного и натурального логарифмов. Тема: Логарифм числа и его свойства.
|
|
Середина урока
4-18 мин
|
Изучение новой темы
Урок проводится с использованием элементов технологии управления качеством обучения в общеобразовательной школе «Биоинформатика и синергетика», автор кандидат педагогических наук, профессор Вассерман Ф.Я..
Объяснение нового материала учитель проводит в виде беседы с учениками, в ходе которой они, отвечая на систему наводящих вопросов, приходят к новым выводам и понятиям.
Преподаватель:
- Итак, определение: Логарифм числа b по основанию a (обозначение: loga b) определяется как показатель степени, в которую надо возвести число a (основание логарифма, где a > 0, a ≠ 1), чтобы получить число b (b > 0).
То есть logab = x означает, что ax = b.
Обозначение loga b - произносится: «логарифм b по основанию a».
- Равносильны ли записи loga b = c и b = ac?
- Тогда вычисление логарифма равносильно решению показательного уравнения
ax = b,
при условии a > 0, a ≠ 1, b > 0,
где x - показатель степени, a - основа степени, b - степень числа a.
- То есть требуется вычислить логарифм
loga b = x,
при условии a > 0, a ≠ 1, b > 0,
где x - логарифм числа b с основой a, a - основа логарифма, b - число, которое стоит под знаком логарифма.
Приводя примеры, учитель использует приёмы скаффолдинга, и даёт учащимся дополнительное время для обдумывания ответов.
- Пример 1: 25 = 32 ⇔ 5 = log2 32.
- Пример 2: 34 = 81 ⇔ 4 = log3 81.
- Пример 3: log1/5 125 = -3 ⇔ (1/5)-3 = 125.
- Пример 4: log1/2 16 = - 4 ⇔ (1/2)-4 = 16.
- Пример 5: найти логарифм: log4 8.
Обозначим log4 8 через x: log4 8 = x.
Перейдем к показательному уравнению: 4x = 8.
Сведем показательное уравнение к основе 2 и решим его: 22x = 23,
2x = 3, x = 3/2.
Ответ: log4 8 = 3/2.
- Пример 6: найти x, если logx 125 = 3/2.
Из определения логарифма имеем: x3/2 = 125.
Возведем обе части в степень 2/3 и воспользуемся свойствами степеней:
(x3/2)2/3 = 1252/3, x = (53)2/3 = 53·2/3 = 52 = 25.
Ответ: x = 25.
- Определение: десятичный логарифм - логарифм по основанию 10.
Другими словами, десятичный логарифм числа b является решением уравнения 10x = b.
Обозначение: десятичный логарифм обозначается lg x или log x.
- Пример 7: lg 100 = lg 102 = 2.
- Пример 8: lg 1000 = lg 103 = 3.
- Пример 9: lg 0.1 = lg 10-1 = -1.
- Пример 10: lg 0.01 = lg 10-2 = -2.
- Пример 11: lg 0.001 = lg 10-3 = -3.
- Определение: натуральный логарифм - логарифм основанием, которого является число e.
Другими словами, натуральный логарифм числа b является решением уравнения ex = b.
Обозначение: натуральный логарифм обозначается ln x.
Чаще всего е называется числом Эйлера, так как с помощью приёма Эйлера в 1766 году Ламбертом было доказано, что число е иррационально.
e = 2,718281828459045235…, для его запоминания используют двустишие:
«Помнить е – закон простой:
Два, семь, дважды Лев Толстой», поскольку 1828 – год рождения писателя Л.Н. Толстого.
Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики, так как функция ex, как вы знаете, не меняется при интегрировании и дифференцировании.
|
Абылкасымова А.Е. «Алгебра и начала анализа, 11 класс» / Алматы «Мектеп», 2019г.
Степанова Т.С. «Математика. Весь школьный курс в таблицах» / Минск «Букмастер», 2015 г.
Рустюмова И.П. «Пособие для подготовки к единому национальному тестированию по математике» / Алматы, 2010 г.
Рустюмова И.П. «Тренажёр для подготовки к единому национальному тестированию по математике» / Алматы, 2010 г.
Сканави М.И. «Сборник задач по математике для поступающих во ВТУЗы» / Москва «Столетие», 1998г.
|
19-35 мин
|
Закрепление изученного материала
Для закрепления материала учащиеся выполняют задания по тренажёру с дифференцированными заданиями трёх уровней сложности:
НПС – нижний порог сложности,
ППС – промежуточный порог сложности,
ВПС – верхний порог сложности.
Учащиеся делают синхронно хлопок и приступают к выполнению заданий уровня НПС, учитель двигается по классу и анализирует степень усвоения учебного материала. Важно увидеть в какой части задания дети делают ошибку. Количество заданий, которые нужно выполнить учитель определяет на своё усмотрение (исходя из имеющегося времени урока и уровня подготовленности класса). По окончании работы, учащиеся обмениваются тетрадями, звучит команда «Ручка в руках – это ошибка». Преподаватель без объяснения записывает на доске правильные ответы к каждому заданию, каждый ученик в это
время проверяет тетрадь своего соседа, делая пометки карандашом. На доске расположена матрица посадочных мест, например, такая:
|

|
В неё преподаватель вносит результаты заданий: «+» и «-». Если класс вышел на норму 63% выполнения, то учитель может переходить на следующий уровень сложности ППС (но надо помнить о том, что необходимо решить задания на все виды логарифма). Если этого не произошло, учитель приступает ко второму объяснению.
НПС
|
ППС
|
ВПС
|
Найти логарифмы следующих чисел по основанию 3
|
Чему равны логарифмы следующих чисел по основанию 10
|
При каком основании выполняется равенство
|
1
|
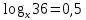
|
1
|
1
|
2
|
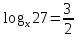
|
2
|
9
|
1
|
100
|
3
|
81
|
2
|
0,001
|
3
|
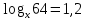
|
4
|
243
|
3
|
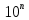
|
4
|
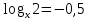
|
5
|
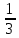
|
4
|
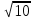
|
Вычислите
|
5
|
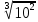
|
5
|
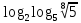
|
6
|
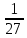
|
6
|
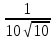
|
6
|
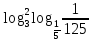
|
Вычислите
|
Вычислите десятичные логарифмы
|
7
|
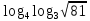
|
7
|
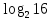
|
8
|
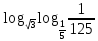
|
8
|
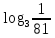
|
7
|
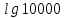
|
9
|
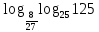
|
9
|
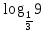
|
8
|
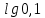
|
10
|
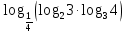
|
10
|
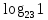
|
9
|
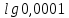
|
|
11
|
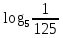
|
10
|
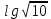
|
Вычислите натуральные логарифмы
|
12
|
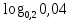
|
Запишите следующие показательные равенства в виде логарифмических
|
11
|
ln e
|
12
|
ln 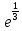
|
13
|
ln 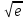
|
14
|
ln 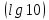
|
13
|
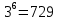
|
|
14
|
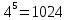
|
15
|
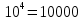
|
16
|
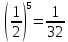
|
17
|
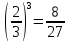
|
18
|
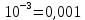
|
Запишите следующие логарифмические равенства в виде показательных
|
19
|
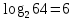
|
20
|
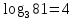
|
21
|
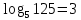
|
22
|
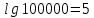
|
23
|
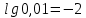
|
24
|
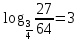
|
Ответы:
НПС
|
ППС
|
ВПС
|
1
|
0
|
1
|
2
|
1
|
1296
|
2
|
2
|
2
|
-3
|
2
|
9
|
3
|
4
|
3
|
n
|
3
|
32
|
4
|
5
|
4
|
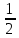
|
4
|
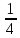
|
5
|
-1
|
5
|
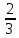
|
5
|
-3
|
6
|
-3
|
6
|
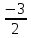
|
6
|
1
|
7
|
4
|
7
|
4
|
7
|
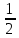
|
8
|
-4
|
8
|
-1
|
8
|
2
|
9
|
-2
|
9
|
-4
|
9
|
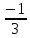
|
10
|
0
|
10
|
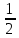
|
10
|
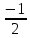
|
11
|
-3
|
11
|
1
|
|
|
12
|
2
|
12
|
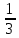
|
|
|
13
|
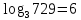
|
13
|
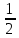
|
|
|
14
|
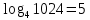
|
14
|
0
|
|
|
15
|
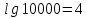
|
|
|
|
|
16
|
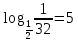
|
|
|
|
|
17
|
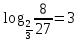
|
|
|
|
|
18
|
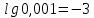
|
|
|
|
|
19
|
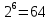
|
|
|
|
|
20
|
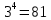
|
|
|
|
|
21
|
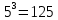
|
|
|
|
|
22
|
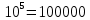
|
|
|
|
|
23
|
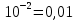
|
|
|
|
|
24
|
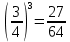
|
|
|
|
|
Если ученик успешно справляется с заданиями из таблицы, то ему учитель может предложить задания более высокого уровня сложности:
1. Между какими целыми числами заключается значение логарифма числа:
1) 7, 30, 120, 495 – по основанию 2;
2) 3, 18, 134, 1782 – по основанию 10?
2. Между какими отрицательными целыми числами заключается значение логарифма чисел:
1) 0,07; 0,018; 0,00125; 0,00005 – по основанию 10;
2) 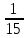 , , 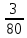 , , 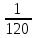 – по основанию 2? – по основанию 2?
3. 1) Чему равен логарифм числа 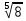 по основанию 2; по основанию 2; 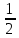 ; 4; 16; 64? ; 4; 16; 64?
2) При каком основании а значение 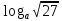 равно равно 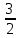 ; ; 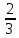 ; ; 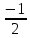 ; ; 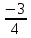 ? ?
4. Показать в общем виде, что если числа образуют геометрическую прогрессию с положительными членами, то логарифмы этих чисел образуют арифметическую прогрессию.
Ответы:
1. 1) (2; 3), (4; 5), (6; 7), (8; 9).
2) (0; 1), (1; 2), (2; 3), (3; 4).
2. 1) (-2; -1), (-2; -1), (-3; -2), (-5; -4).
2) (-4; -3), (-5; -4), (-7; -6).
3. 1) 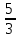 ; ; 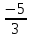 ; ; 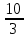 ; ; 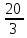 ; -10. ; -10.
2) 3; 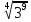 ; ; 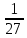 ; ; 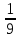 . .
|
|
Конец урока
36-38 мин
|
Рефлексия
|
|
39-40 мин
|
Домашнее задание
Учитель даёт необходимые пояснения по выполнению заданий:
1. Представьте логарифм в виде степени:
a) 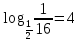 b) b) 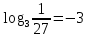
2. Вычислите:
a) 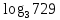 b) b) 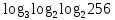
3. Найдите неизвестное, используя определение логарифма:
a) 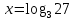 ; b) ; b) 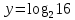 ; c) ; c) 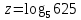 ; ;
d) 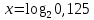 ; e) ; e) 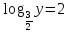 ; f) ; f) 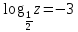 . .
Ответы:
1. a) 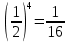 ; b) ; b) 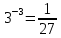 . .
2. a) 6; b) 1.
3. a) 3; b) 4; c) 4; d) -3; e) 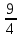 ; f) 8. ; f) 8.
|
|
Дополнительная информация
|
Дифференциация - как вы планируете оказывать больше поддержки? Как вы планируете давать задания более способным учащимся?
|
Междисциплинарные связи
Безопасность жизнедеятельности
ИКТ связи
Связи с ценностями
|
1. Дифференциация учебного материала:
- учащиеся с низким уровнем обучаемости на первых этапах изучения нового материала могут не сразу отвечать на вопросы учителя,
- для сильных учащихся заготовлена карточка повышенной сложности.
2. Дифференциация работы по характеру помощи учащимся (препод. оказывает помощь сильным учащимся, которые работают по индивидуальному плану).
3. Дифференциация работы учащихся по степени самостоятельности (практически все учащиеся работают самостоятельно, помощь получают только сильные учащиеся по мере необходимости в ней).
|
- соблюдение правил безопасности;
- чередование форм и видов деятельности.
|
Оценивание - как вы планируете проверить знания учащихся?
|
1. Наблюдения преподавателя.
2. Взаимооценивание заданий по готовым ответам.
3. Самооценивание по итогам заполнения посадочной матрицы.
4. Самооценивание эффективности работы на уроке на этапе рефлексии.
|
Используйте графу ниже, чтобы проанализировать Ваш урок. Ответьте на самые актуальные вопросы о проведенном уроке.
|
|
Сводная оценка
Какие два аспекта прошли очень хорошо (рассмотрите преподавание и обучение)?
1:
2:
Какие два аспекта улучшили бы урок (рассмотрите преподавание и обучение)?
1:
2:
Что я узнал о классе или об отдельных учащихся на данном уроке, что я учту на следующем уроке?
|
|
 Скачать 214.8 Kb.
Скачать 214.8 Kb.
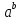 ? / ожидаемый ответ: степень.
? / ожидаемый ответ: степень.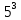 . / ожидаемый ответ: 125.
. / ожидаемый ответ: 125.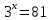 . Действие, по средствам которого находится показатель х степени по значению степени 81 и основанию 3, называется нахождением логарифма.
. Действие, по средствам которого находится показатель х степени по значению степени 81 и основанию 3, называется нахождением логарифма.
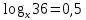
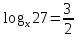
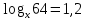
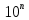
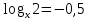
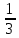
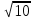
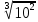
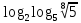
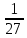
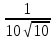
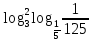
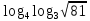
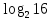
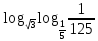
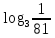
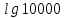
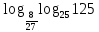
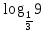
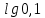
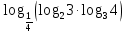
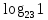
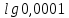
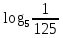
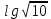
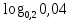
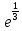
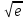
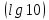
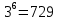
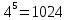
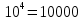
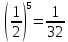
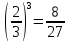
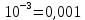
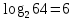
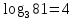
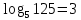
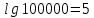
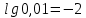
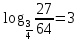
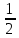
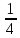
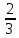
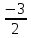
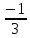
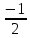
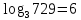
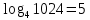
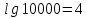
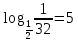
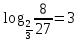
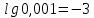
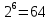
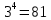
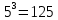
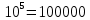
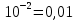
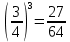
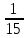 ,
, 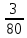 ,
, 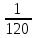 – по основанию 2?
– по основанию 2?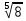 по основанию 2;
по основанию 2; 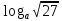 равно
равно 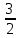 ;
; 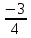 ?
?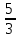 ;
; 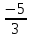 ;
; 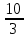 ;
; 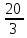 ; -10.
; -10.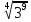 ;
; 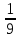 .
.
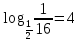 b)
b) 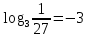
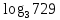 b)
b) 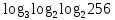
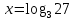 ; b)
; b) 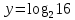 ; c)
; c) 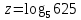 ;
;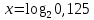 ; e)
; e) 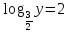 ; f)
; f) 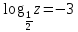 .
.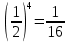 ; b)
; b) 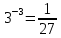 .
.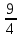 ; f) 8.
; f) 8.