Методы решения логарифмических уравнений.
|
Метод решения на основании определения логарифма.
|
Теорема.
Уравнения 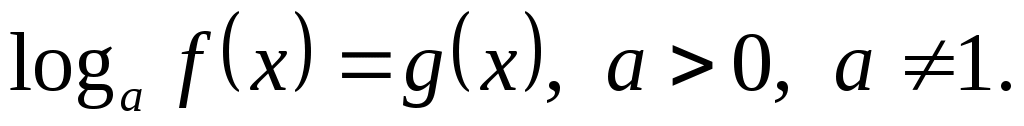 и и 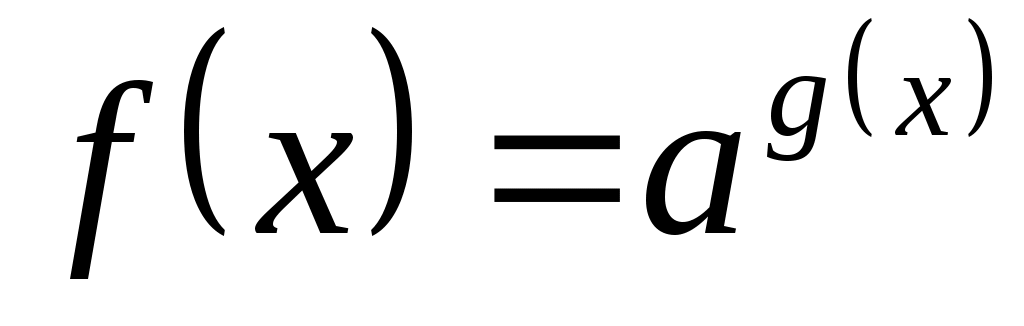 равносильны равносильны
|
Метод потенцирования.
|
Пусть 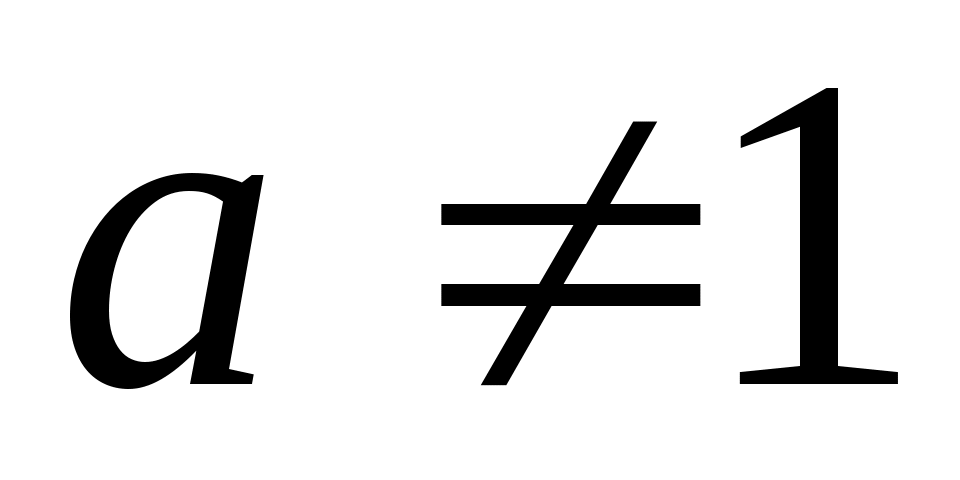 – фиксированное положительное число и пусть дано уравнение – фиксированное положительное число и пусть дано уравнение 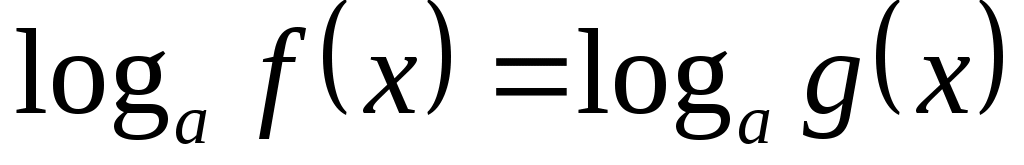 . Замену этого уравнения уравнением . Замену этого уравнения уравнением 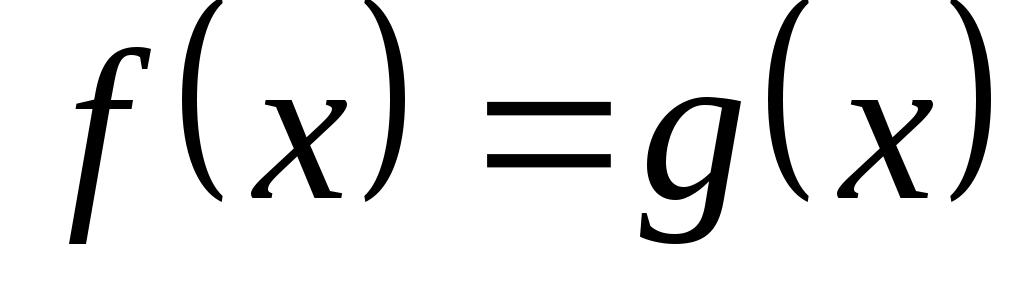 называют потенцированием уравнения называют потенцированием уравнения 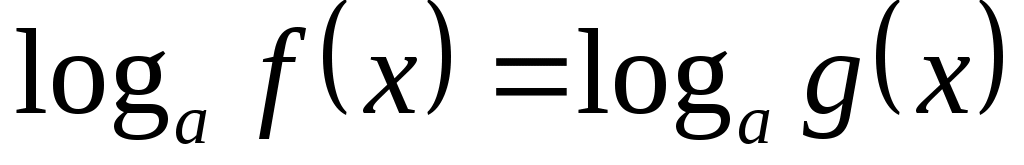 . .
Замечание. Потенцирование уравнения может привести к появлению посторонних корней.
Пример.
Уравнение lg (x2 – 4) = lg (4x – 7) приводит к уравнению – следствию (x2 – 4) = (4x – 7), имеющему
корень 1, посторонний для исходного уравнения.
|
Теорема.
Уравнение 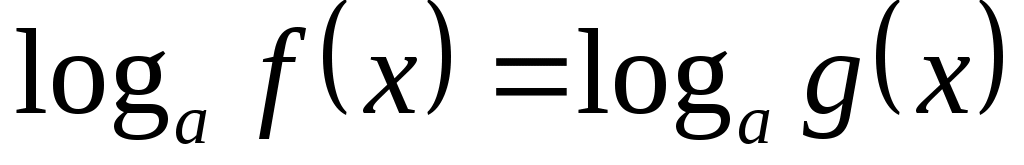 равносильно любой из систем: равносильно любой из систем:
|
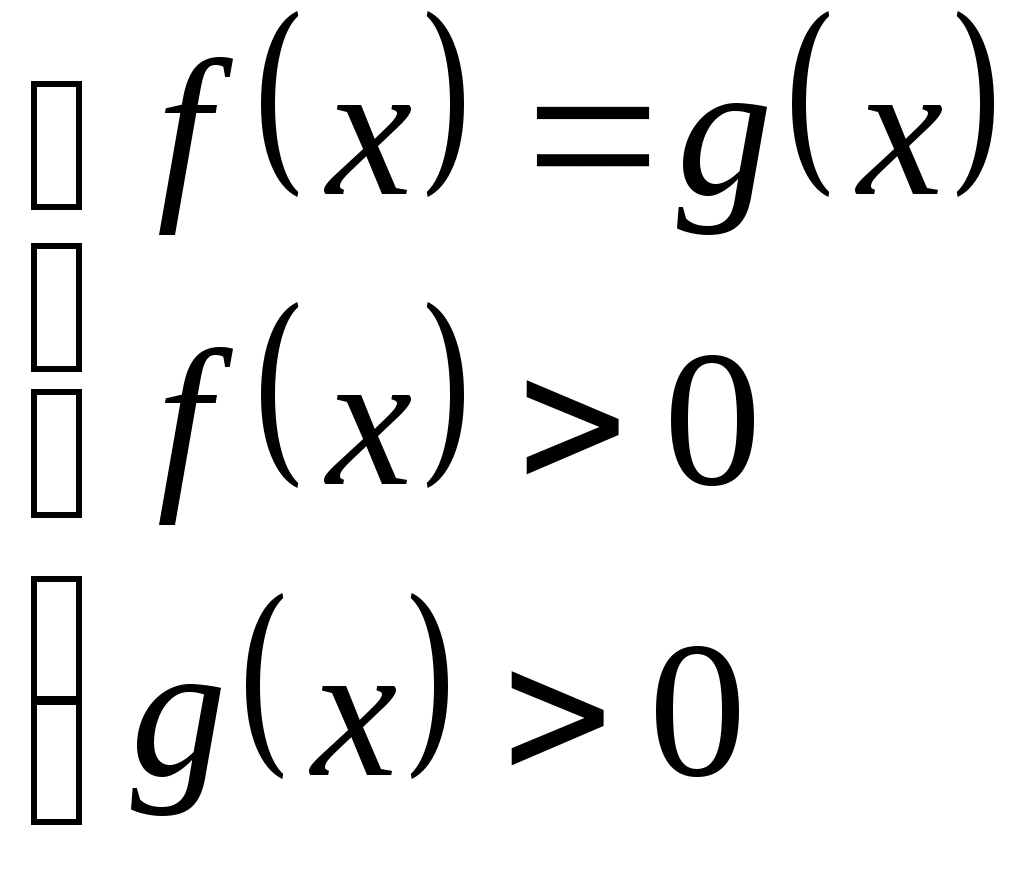
|
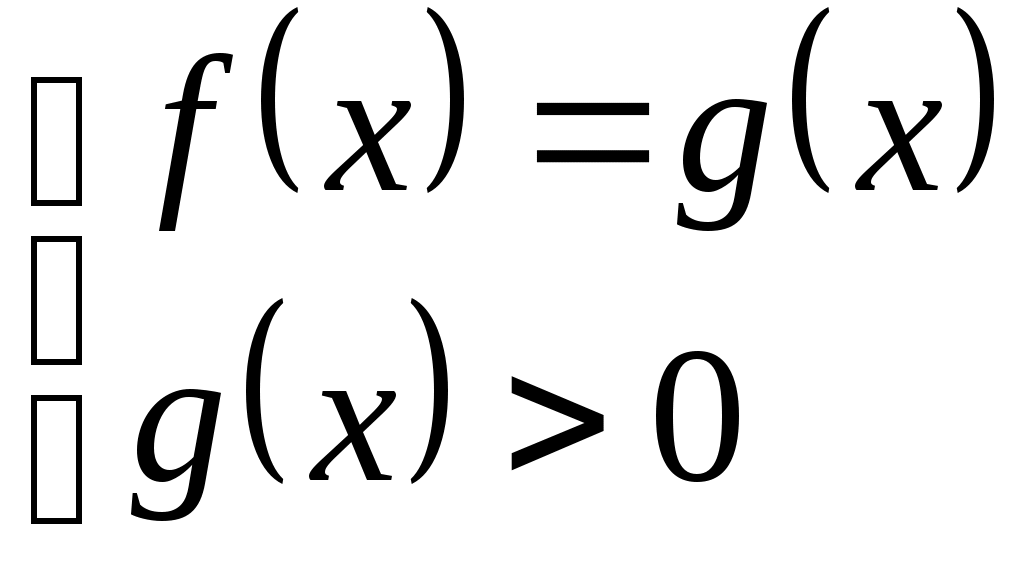
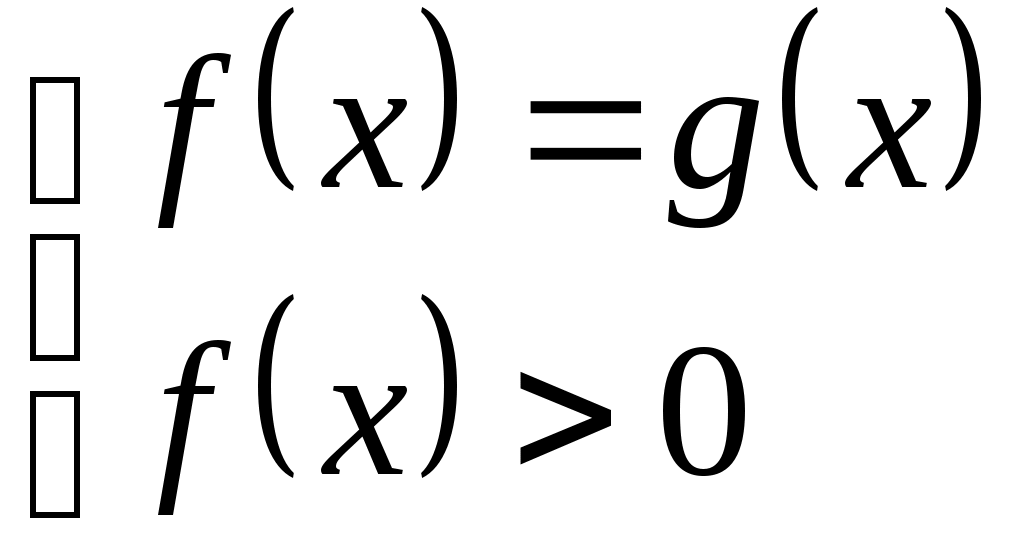
|
Теорема.
Уравнение 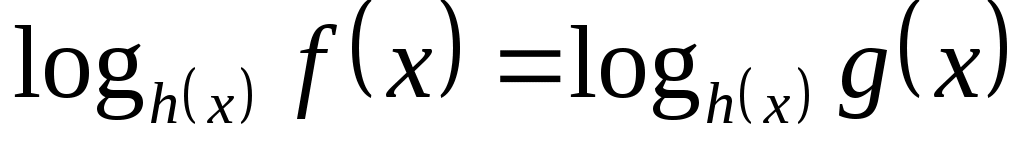 равносильно любой из систем: равносильно любой из систем:
|
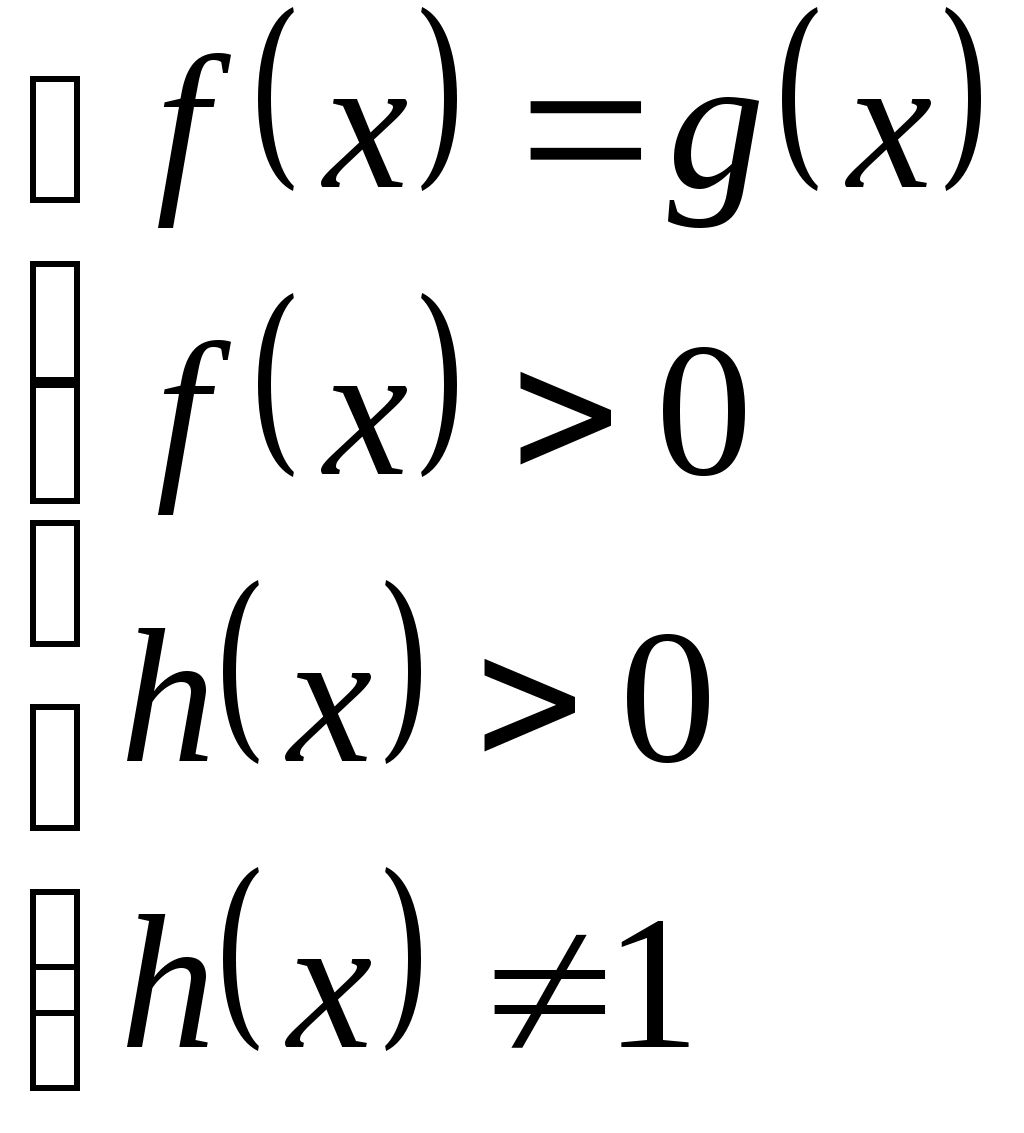
|
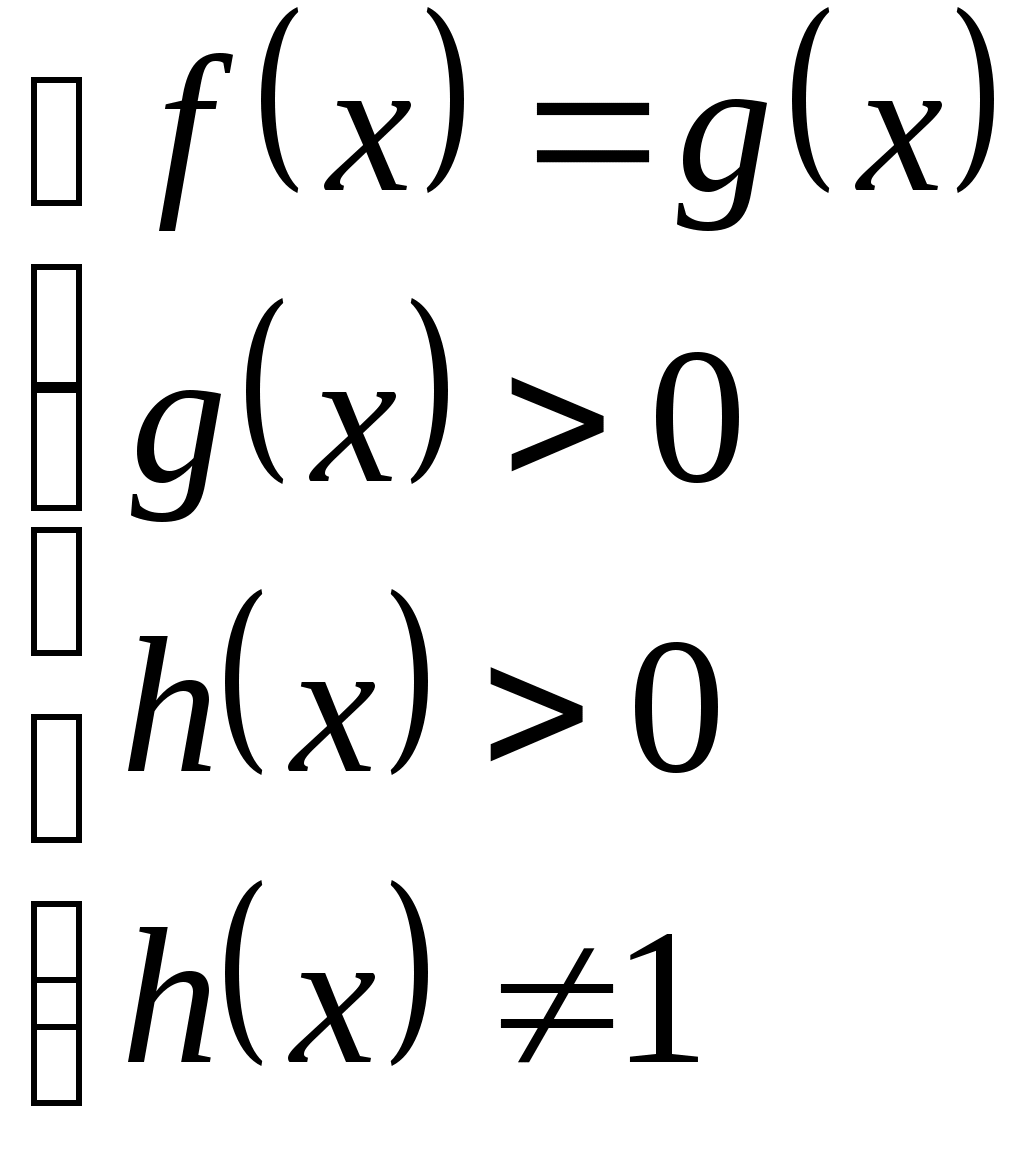
|
Теорема.
Уравнение 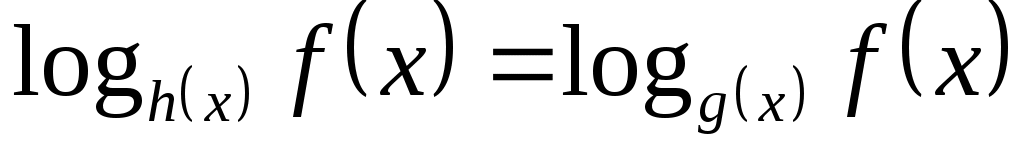 , где , где 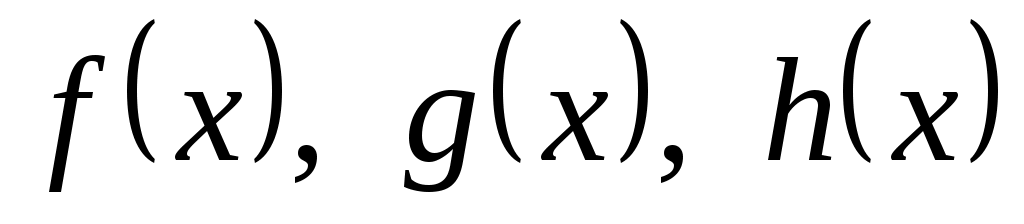 – заданные функции равносильно любой из систем: – заданные функции равносильно любой из систем:
|
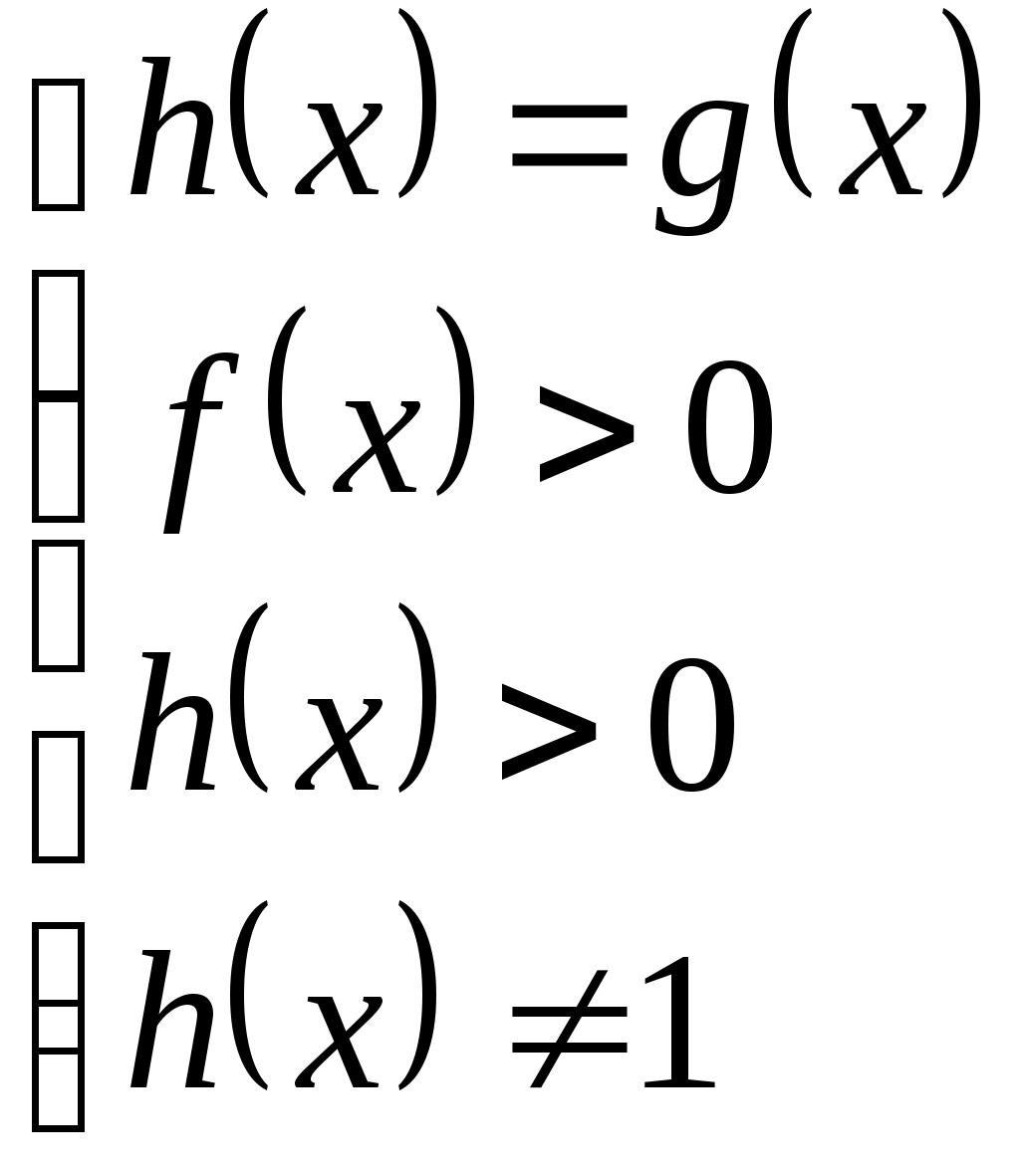
|
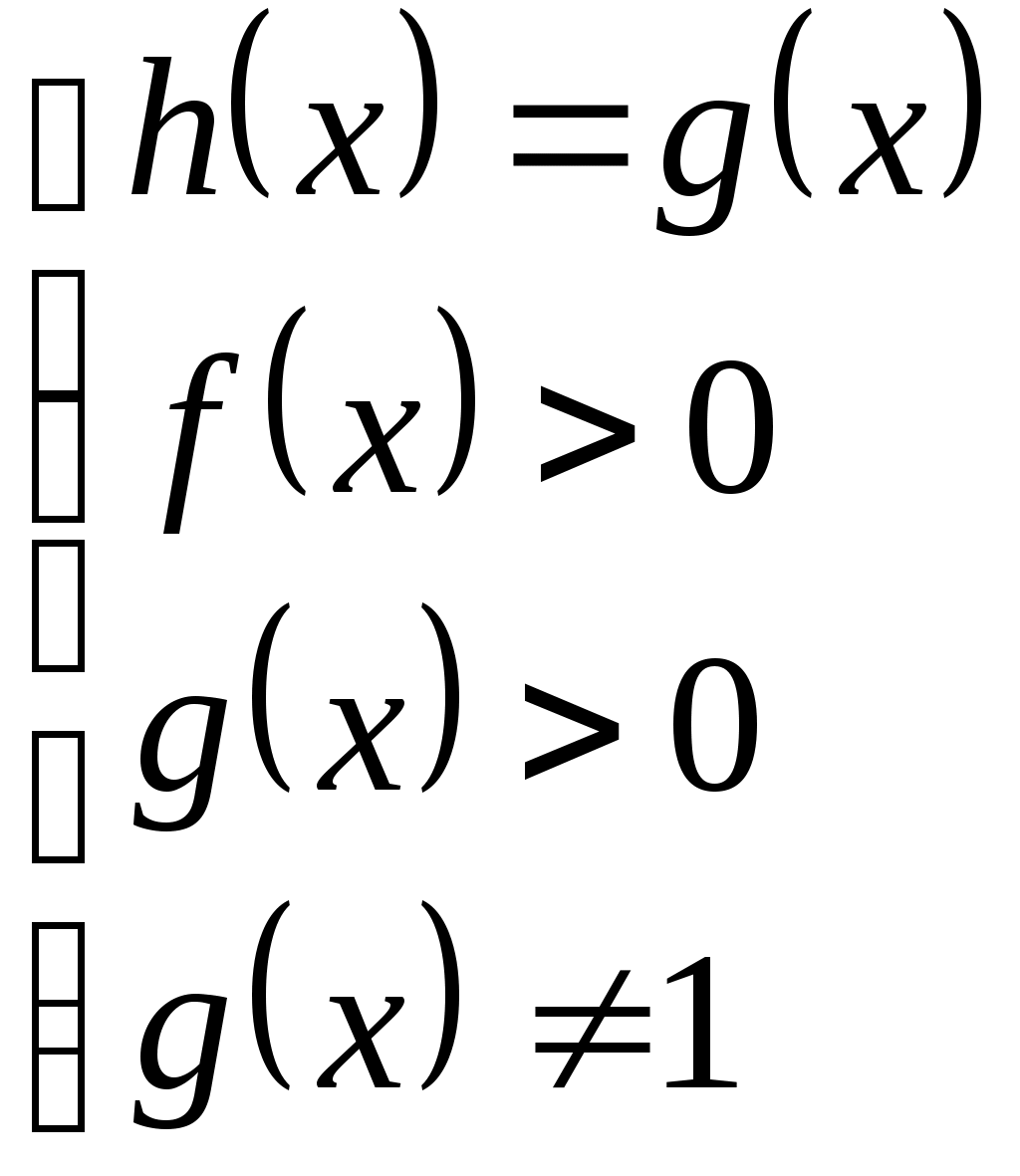
|
Метод введения новой переменной.
|
Уравнение
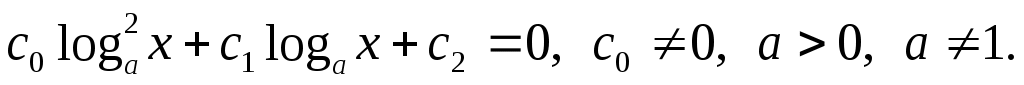
Обозначив 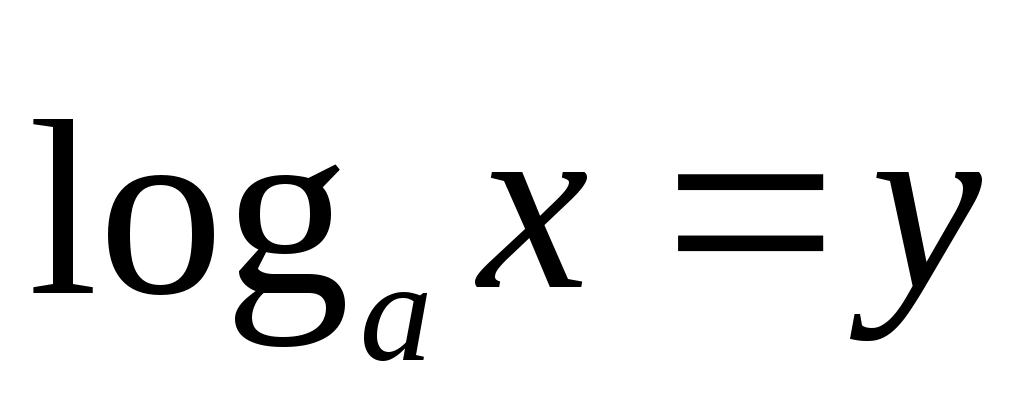 и, решив полученное квадратное уравнение, придём к уравнению типа 1). и, решив полученное квадратное уравнение, придём к уравнению типа 1).
Отметим, что часто исходное уравнение сводится к одному из указанных типов после некоторых преобразований.
|
 Скачать 3.34 Mb.
Скачать 3.34 Mb.