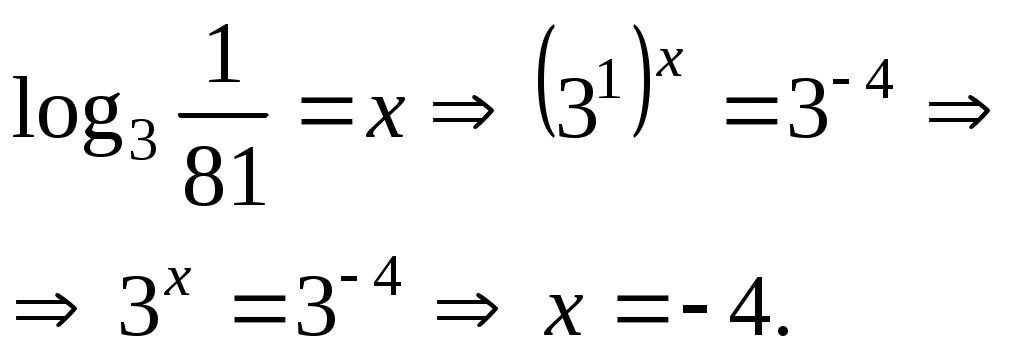Логарифмы 10к. логарифмы
 Скачать 3.34 Mb.
|
Откуда взялся Log?Мы изучили показательные уравнения. Давайте повторим, решив одно из них.  = 32. (1) Запишем данное уравнение так: = , откуда х = 5.Напомним, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 2. А теперь, попробуем решить еще одно показательное уравнение. = 30. (2)Теперь, тех знаний с точки зрения решения показательных уравнений, недостаточно. Есть ли корень у этого показательного уравнения? Да, есть. Как его найти, если уравнение не решается привычным способом? И теперь, мы введем понятие «логарифм», которое поможет нам решить данное уравнение. Важно запомнить! Логарифм (от греч. λόγος – «слово», «отношение», άριθμός - «число») определяется как показатель степени, в которую надо возвести основание, чтобы получить число. Для начала, представим наши показательные уравнения в виде стандартной формы (т.е. заменим числа с правой и левой стороны на а и b), напишем:  = b.Важно запомнить! Корень х уравнения = b будем находить так:х =  b, где а >0, а 1, b >0.Соотнесем теперь определение логарифма с (1) показательным уравнением: = 32 х = 32 х = 5, так как = 32Значит, 32 = 5, так как = 32.Мы решили показательное уравнение с помощью применение логарифма. Теперь, представим (2) показательное уравнение в виде логарифма и попробуем решить его: = 30 х = 30.х = 30 – это и есть корень уравнения = 30. На инженерном калькуляторе это будет приблизительно.Так откуда же взялся логарифм? А он взялся из-за потребности решить показательное уравнение, которое не решается привычным способом. Свойства логарифмовТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ЛОГАРИФМИЧЕСКИХ И ПОКАЗАТЕЛЬНЫХ ВЫРАЖЕНИЙ 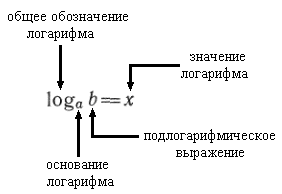 Логарифмом числа bпо основанию а  называется показатель степени, в которую надо возвести число а, чтобы получилось b: Основное логарифмическое тождество 
| ||||||||||||
и аргумент
в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
уравнение: 
в 
следует, что логарифм не считается.