логика. ответы к экзамену логика. Логика наука о мышлении, ее предметом, являются законы и формы, приемы и операции мышления, с помощью которых человек познает окружающий его мир
 Скачать 2.69 Mb. Скачать 2.69 Mb.
|
Виды понятий по объему и содержанию.Понятия по объёму делятся на непустые(единичные и общие) и пустые(с нулевым объёмом(Баба-Яга)). Понятия делятся наединичные(Пушкин) и общие(автомобиль) в зависимости от того, мыслится в них один элемент или множество элементов. По содержанию выделяют 4 типа понятий: 1. Конкретные и абстрактные. Понятие, в котором мыслится предмет или совокупность предметов как нечто самостоятельно существующее, называетсяконкретным(Дом); понятие, в котором мыслится признак предмета или отношение между предметами, называетсяабстрактным(Белизна). 2.Безотносительные и относительные. Понятия, отражающие предметы, существующие раздельно и мыслящиеся вне их отношения к другим предметам, называются безотносительными.( «студент», «государство»).Относительные понятия содержат признаки, указывающие на отношение одного понятия к другому понятию. (Дети-родители) 3. Положительные и отрицательные. Понятия, содержание которых составляют свойства, присущие предмету, называютсяположительными.(Мошенник) Понятия, в содержании которых указывается на отсутствие у предмета определенных свойств, называютсяотрицательными.(Не грамотный человек). Собирательные и несобирательные.Понятия, в которых мыслятся признаки некоторой совокупности элементов, составляющих единое целое, называются собирательными. (Коллектив) Понятие, в котором мыслятся признаки, относящиеся к каждому его элементу, называетсянесобирательным. (Судья) Отношения между понятиями.1.Равнозначны-понятия,которые различаются по содержанию,но имеют равный объём.(Рим=столица Италии) 2.Отношение подчинения-объём одного понятия целиком включается в объём другого понятия(Ель-дерево). 3.Понятие одновременно может быть видом по отношению и к более общему и к менее общему. (Человек-славянин-русский). 4.Отношение пересечения-где объём одного понятия частично входит в объём другого(Студент,нумизмат) Существуют три вида отношений несовместимости: 1)соподчинение (координация), 2) противоположность, 3) противоречие 1. В отношениисоподчинения (координации) находятся два или больше неперекрещивающихся понятий, подчиненных общему для них понятию. Понятия, находящиеся в отношении подчинения к общему для них понятию, называютсясоподчиненными.(Пианино и скрипка-музыкальные инструменты). 2. В отношениипротивоположности находятся понятия, одно из которых содержит некоторые признаки, а другое — признаки, не совместимые с ними. Объемы двух противоположных понятий составляют в своей сумме лишь часть объема общего для них родового понятия, видами которого они являются и которому они соподчинены. (Белые туфли-чёрные туфли). 3. В отношениипротиворечия находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки исключает.(Высокий дом-невысокий дом) Объемы двух противоречащих понятий составляют весь объем рода, видами которого они являются и которому они соподчинены. Они изображаются с помощью круговых схем- кругов Эйлера. Виды понятий по объему и содержанию. Из выясненного выше применительно к классам (подклассам, элементам классов), очевидно существование 3-х видов понятий по объёму: 1). единичные понятия — это те, объём которых составляет одноэлементный класс; 2) общие понятия — это те, объём которых составляет более чем одноэлементный (общий) класс; 3) пустые (нулевые) понятия — это те, объём которых представляет пустое множество (по фактическому или по логическому основаниям). Пример Единичные понятия могут быть понятиями, как об материальных, так и духовных предметах мысли: к 1-ой категории принадлежит понятие «В.В. Путин», ко 2-ой — понятие «сегодняшняя последняя медитация Далай-Ламы». По отношению к понятию «В.В. Путин» в качестве общего (родового) укажем понятие «человек». Фактически пустое понятие — «президент В.В. Путин, рождённый в США», логически нулевое — «рассосредоточенная соредоточенность». В силу того, что существенные признаки разных понятий оказываются типически разными, закономерно существуют виды понятий в аспекте их содержания: 1). Абстрактные понятия, т. е. такие, в которых мыслится не целый предмет, а какой-либо из признаков предмета, мыслимый отдельно от самого предмета. 2). Конкретные понятия, т. е. такие, в которых мыслится предмет или совокупность предметов как нечто самостоятельно существующее. 3). Положительные понятия, т. е. те, в которых мыслится наличие у предмета того или иного признака (свойства, качества, отношения). 4). Отрицательные понятия, т. е. те, в которых мыслится (означается) именно отсутствие у предмета того или иного признака (свойства, качества, отношения). 5). Собирательные понятия, т. е. в которых совокупность предметов (группа однородных предметов) мыслится как некое действительное единство (целое), так что сущностные признаки этого единства нельзя перенести ни на один из элементов данной совокупности. 6). Несобирательные (разделительные) понятия, т. е. в которых содержание понятия можно отнести к каждому отдельному предмету (элементу) этого мыслимого в понятии класса. 7). Относительные понятия, т. е. такие, в которых мыслятся предметы, существование одного из которых предполагает существование другого. 8). Безотносительные понятия, т. е. такие, в которых мыслятся самостоятельно существующие предметы, т. е . существующие вне зависимости от какого-либо другого предмета. Пример Абстрактные понятия: твёрдость, гибкость, умение. Конкретные понятия: корунд, ивовый прут, человек, практично использующий свой разум. Положительные понятия: зеркало, толковый (пследнее понятие превратим, введя отрицание, в противоречащее ему отрицательное понятие — бестолковый). Отрицательные понятия: беспечный путешественник, студент, безработный художник, но не являются отрицательными понятиями, хотя и содержат в своём составе отрицательные частицы (поскольку данные отрицательные частицы слились с соответствующими словами, корни которых утратили собственный отдельный смысл: неряха, недотёпа, ненастье (что такое «настье»?). Отрицательные понятия в языке выражены языковыми знаками, содержащими какую-либо отрицательную частицу («не-», «без-», «противо-», «анти-» и т. п.), выполняющую функцию отрицания. Если же слово или словосочетание имеет в своей структуре отрицательную частицу, которая не выполняет функции отрицания (нелепый, безалаберный), то выражаемое таким словом или словосочетанием понятие является опять-таки положительным. Если мы вносим в структуру какого-либо положительного понятия (А) отрицательную частицу, которая призвана выполнить и действительно выполняет функцию отрицания, то тем самым получаем из исходного понятия А противоречащее ему (находящееся с понятием А в отношении контрадикторности) отрицательное понятие не-А. Собирательные понятия: стая, созвездие, соцветие (установить, что какое-либо понятие является собирательным можно посредством рассуждения: если о любом элементе класса животных можно утверждать, что это именно животное, то, зная, что лес состоит из деревьев (дерево — элемент данного класса), ни об одном дереве мы не можем сказать, что оно есть лес, значит, понятие лес является собирательным). Используем в разных высказываниях (суждениях) понятие «студенты группы СО-211»: 1) «студенты группы СО-211 провели коллективное мероприятие»; 2) «зачёт по логике и теории аргументации был сдан студентами группы СО-211». В 1-ом суждении понятие «студенты группы СО-211» является собирательным, поскольку это понятие о едином коллективе, т. е. о единичном в аспекте объёма понятии. Во 2-ом суждении данное общее понятие использовано в разделительном (несобирательном) смысле: каждый студент группы СО-211 обладает признаком «быть сдавшим зачёт по логике и теории аргументации». Несобирательные понятия: звезда, осень, индивид. Относительные понятия: ученик, угнетатель, творение (без учителя не мыслим ученик, без угнетённого — угнетатель, без творца — творение). Безотносительные понятия: книга, город, столица Российской Федерации. Итак, понятия следует различать по объёму и по содержанию. Осознавая вид понятия в аспекте его объёма и его содержания, мы вполне овладеваем сутью той мысли, которая оформлена данным понятием. Показателем степени такого овладения в частности служит умение давать любому понятию логическую характеристику (общую логическую характеристику), т. е. умение правильно (аргументировано, безошибочно) установить вид понятия в количественном и качественном аспектах. Пример Логическая характеристика некоторых понятий: стол (общее, конкретное, положительное, несобирательное (разделительное), безотносительное понятие); эта небрежность гения (единичное, абстрактное, отрицательное, несобирательное, безотносительное понятие); мать своего собственного отца (нулевое, конкретное, положительное, несобирательное, относительное понятие). Отношения между понятиями. Между понятиями можно установить разнообразные отношения по содержанию и объему. По содержанию различают сравнимые и несравнимые понятия. Несравнимыми называются понятия, в содержании которых нет общего родового признака (они не принадлежат к одному роду). Например, «тангенс» (род — «тригонометрическая функция») и «дерево» (род — «растение»). Сравнимые — понятия, в содержании которых имеется хотя бы один общий существенный признак (они принадлежат к одному роду). Например, понятия «лингвистика» и «логика» имеют общее родовое понятие «наука»; понятия «дворник» и «студент» — общее родовое понятие «человек». Сравнимые понятия по объему разделяются на совместимые и несовместимые (рис. 4). Для иллюстрации отношений между объемами понятий используют диаграммы Эйлера — Венна. Принцип применения их таков: каждый круг обозначает объем какого-либо понятия, а каждая точка круга — отдельный элемент этого объема. 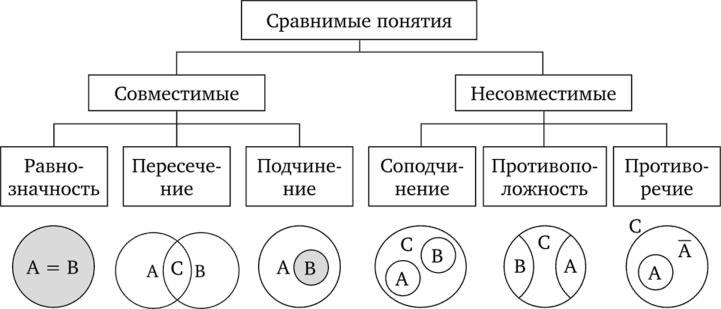 Рис. 4 Понятия совместимы, если они имеют общие элементы объема. Совместимые понятия могут находиться в следующих отношениях: 1. Равнозначность (равнообъемность, эквивалентность). Понятия находятся в отношениях равнозначности, если у них полностью совпадают объемы. Графически объемы таких понятий сливаются в одном круге Эйлера. Например, «равносторонний прямоугольник» (А) и «квадрат» (В). 2. Пересечение. Если в понятиях зафиксированы как общие, так и различные признаки, то их объемы совпадают лишь в некоторой своей части и изображаются пересекающимися окружностями. Например, «лыжник» (А) и «стрелок» (В). Общая часть двух кругов обозначает образованный в результате пересечения объемов двух понятий объем нового понятия (биатлонист (С)). 3. Подчинение (включение). Понятия находятся в отношении подчинения (включения), если объем одного понятия полностью входит в объем другого, но не исчерпывает его. Из двух понятий, находящихся в отношении подчинения, понятие с большим объемом (подчиняющее) является родовым, или родом (А), по отношению к понятию с меньшим объемом, которое по отношению к первому называется видовым или видом (В). Например, родовое понятие «млекопитающее» (А) и видовое — «человек» (В). Отношения рода и вида следует отличать от отношений части и целого. Вид обладает всеми признаками рода, а часть не обладает признаками целого. Например, понятие «береза» относится к понятию «дерево» как вид к роду, потому что береза обладает всеми признаками дерева. Понятия же «ствол» и «дерево» соотносятся как часть и целое, потому что ствол не обладает признаками дерева и не является его разновидностью. Родовидовые понятия лежат в основе логических операций ограничения и обобщения понятий, деления объема понятий и некоторых видов определения. Понятия несовместимы, если они не имеют общих элементов объема. Для изображения отношений несовместимых понятий нужно ввести более широкое по объему понятие, которое включало бы объемы несовместимых понятий. Несовместимые понятия могут находиться по отношению друг к другу в определенных отношениях. 1. Соподчинение (координация). Понятия А и В находятся в отношении соподчинения, если они совместно подчинены третьему понятию С, как виды подчинены роду. При этом объемы понятий А и В не исчерпывают объем родового понятия С. В отношении соподчинения находятся понятия «береза» (А) и «баобаб» (В); С — понятие «дерево». 2. Противоположность (контрарность). В отношении противоположности находятся объемы таких понятий, которые содержат противоположные признаки в пределах одного рода. Слова, выражающие противоположные понятия, являются антонимами. Противоположными (контрарными) будут понятия «белый» — «черный», «любовь» — «ненависть». 3. Противоречие (контрадикторность). В отличие от двух предыдущих случаев, понятия, находящиеся в отношении противоречия полностью исчерпывают объем какого-то универсального класса (С). В отношении логического противоречия находятся такие понятия, одно из которых утверждает наличие определенных признаков (А), а другое — отрицает их (не А). Противоречивые (контрадикторные) понятия «белый» (А) и «небелый» (не А) исчерпывают объем родового понятия «цвет» (С). Обобщение и ограничение понятий. Логические операции обобщения и ограничения основаны на законе обратного соотношения между содержанием и объемом понятия и являются взаимообратными. Предположим, мы знаем, что кто-то — студент, и хотим уточнить наши знания о нем. Уточняем: это студент первого курса факультета управления и политики МГИМО Иванов Сергей. Произведенная логическая операция есть операция ограничения понятия. Ограничение понятия — это логическая операция перехода от родового понятия к видовому путем добавления к содержанию данного понятия видообразующего признака. Ограничить понятие — значит перейти от понятия с большим объемом, но меньшим содержанием к понятию с меньшим объемом, но большим содержанием. Например, треугольник — равнобедренный треугольник. Сужение объема понятия происходит в результате добавления к содержанию исходного понятия «треугольник» признака «равнобедренный», который принадлежит не всем треугольникам, но лишь их части. Предел ограничения понятия — единичное понятие, в объеме которого содержится только один предмет. Примеры единичных понятий: солнце, Санкт-Петербург, первый космонавт в мире. Противоположной ограничению является операция обобщения понятия. Обобщение понятия — это логическая операция перехода от видового понятия к родовому путем удаления видообразующего признака. Например, равнобедренный треугольник — треугольник. Почти для каждого видового понятия можно найти более широкое по объему родовое понятие. Эти родовые понятия могут включаться в еще более широкие по объему понятия. Однако обобщение имеет предел: нельзя обобщить понятия, не имеющие родовых связей. Такие предельно широкие по своему объему понятия называются категориями. Как правило, категориями являются философские понятия. Примеры категорий: бытие, субъект, сущность, время, пространство, качество, количество, сознание, истина, форма, содержание, причина и др. В процессе обобщения и ограничения понятий переходы от рода к виду следует отличать от отношений целого и части. Например, неправильно обобщать понятие «центр города» до понятия «город» или ограничивать понятие «университет» до понятия «факультет», так как в обоих случаях речь идет не об отношении рода и вида, а об отношении части и целого. Определение понятий. Правила и ошибки определения. Определение (дефиниция) — это логическая операция, при помощи которой раскрывают содержание понятия. Определить понятие — значит выявить существенные характеристики, которые составляют содержание этого понятия. Структура определения состоит из двух компонентов: дефиниендума — понятия, содержание которого раскрывают в определении; дефиниенса — понятия, при помощи которого раскрывают содержание дефиниендума в определении. Дефиниендум сокращенно обозначим «dfd», а дефи- ниеис — «dfn». Приведем пример. Рассмотрим определение «Студент — это человек, обучающийся в вузе». Дефиниендум — студент; Дефиниенс — человек, обучающийся в вузе. Определение — это не просто высказывание естественного языка, как это может показаться с первого взгляда. Это своеобразная конвенция использования языковых конструкций. Так, определение понятия «преступление» в моральных и правовых теориях может иметь различный смысл. Это означает, что между людьми достигнуты различные конвенции по поводу использования этого термина в этих двух случаях. Определения как конвенции не являются утверждениями. Поэтому их нельзя оценить как истинные или ложные. Они могут быть правильными или неправильными, успешными или неуспешными. Существуют различные виды определений. По форме определения делят на: — явные; — неявные. Определение должно быть правильным по своему строению и форме. Существует 4 правила определения: Определения должны быть соразмерны (объёмы равны А=Вс) Нарушение этого правила влечет такие ошибкикак: А) слишком широкое определение– объём определяющего понятия шире определяемого (А В) слишком узкое– объём определяющего уже определяемого (А>Bc) Определение не должно заключать в себе круга., т. е при определении понятия мы используем понятие, которое в свою очередь определяется пи помощи первого(порочный круг) (А определяется через В, а В через А). Разновидность круга тавтология( Неосторожное преступление – преступление, совершенное по неосторожности) Определение должно быть ясным Если понятие определяется через понятии, которое само нуждается в определении, то это ведет к ошибке определения неизвестного через неизвестное(х через у). Определение не должно быть отрицательным, т.к отрицательное определение не раскрывает понятия, оно указывает чем предмет не является не показывает, чем предмет является. Может использоваться только для отрицательных понятий, например можно сказать «Безбожный человек – человек, не признающий существование Бога». |
