логика. ответы к экзамену логика. Логика наука о мышлении, ее предметом, являются законы и формы, приемы и операции мышления, с помощью которых человек познает окружающий его мир
 Скачать 2.69 Mb. Скачать 2.69 Mb.
|
Виды умозаключенийПо направленности логического следования умозаключения делятся на два класса (рис. 29): 1) дедуктивные (достоверные); 2) недедуктивные (вероятностные). 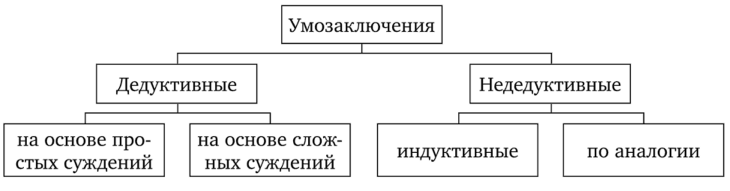 В недедуктивных умозаключениях вывод не следует строго логически из посылок, а лишь в некоторой степени подтверждается посылками. В таком умозаключении истинные посылки не являются достаточным основанием для вывода. До соответствующей проверки вывод не может считаться ни истинным, ни ложным. Недедуктивные умозаключения бывают двух видов: 1) индуктивные; 2) умозаключения по аналогии. Дедуктивные (от лат. deductio — выведение) — умозаключения, у которых между посылками и выводом имеется отношение логического следования. В основе дедукции лежит n-кратная импликация. По числу исходных суждений дедуктивные умозаключения делятся на следующие виды: 1) непосредственные — дедуктивные умозаключения, которые строятся на основе одной посылки; 2) опосредованные — дедуктивные умозаключения, которые строятся на основе двух и более посылок; к опосредованным дедуктивным умозаключениям относятся простой категорический силлогизм, сложные силлогизмы, умозаключения из сложных суждений. По виду исходных суждений дедуктивные умозаключения бывают двух видов: 1) дедуктивные умозаключения на основе простых суждений, в которых учитывается внутренняя структура суждения; 2) дедуктивные умозаключения на основе сложных суждений, в которых учитываются только связи между суждениями, а внутренняя структура суждений не учитывается (выводы логики высказываний). Если дедуктивное умозаключение сделано правильно, то есть рассуждение было корректно, то соответствующая ему формула должна быть тавтологией. Корректность рассуждений проверяют либо табличным, либо алгебраическим способом. 20.Непосредственные дедуктивные умозаключения. Способы их преобразования. Непосредственные умозаключения — это выводы посредством преобразования суждений. Характерной особенностью этих суждений является наличие одной посылки. К непосредственным дедуктивным умозаключениям в традиционной логике относятся следующие: 1) превращение; 2) обращение; 3) противопоставление предикату; 4) противопоставление субъекту; 5) умозаключения по логическому квадрату. 1. Превращение — преобразование суждения по закону двойного отрицания: 1) отрицается связка, то есть меняется качество исходного суждения (утвердительное суждение становится отрицательным и наоборот); 2) отрицается предикат, то есть предикат заменяется противоречащим понятием (не Р). Схема превращения: 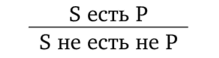 Превращению подлежат суждения А, I, Е, О (рис. 30). 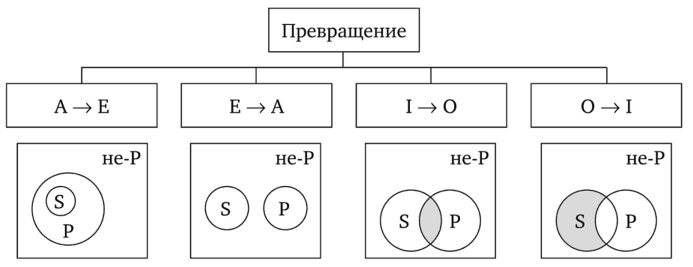 Рис. 30 А —> Е. Общеутвердительное суждение превращается в общеотрицательное с отрицательным предикатом:  Например, суждение «Все студенты нашего курса изучают логику» (А) превращается в суждение «Ни один студент нашего курса не является не изучающим логику» (Е). Е —> А. Общеотрицательное суждение превращается в общеутвердительное:  Например,  I —^ О. Частноутвердительное суждение превращается в частноотрицательное: 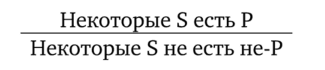 Например,  О —> I. Частноотрицательное суждение превращается в частноутвердительное: 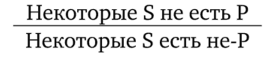 Например,  2. Обращение — преобразование исходного суждения, в результате которого субъект исходного суждения становится предикатом, а предикат — субъектом заключения. Субъект и предикат меняются местами при сохранении качества суждения. Схема обращения: 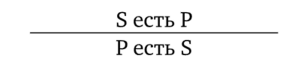 Обращению подлежат суждения А, Е, I (рис. 31). 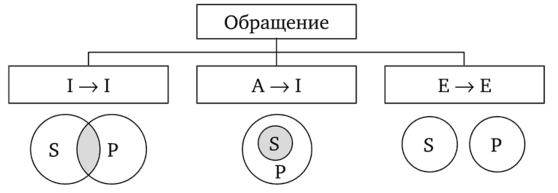 Рис. 31 А —»I. Общеутвердительное суждение обращается в частноутвердительное: 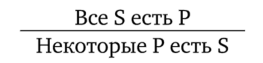 Например,  I —> I. Частноутвердительное суждение обращается в частноутвердительное: 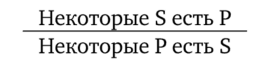 Например, 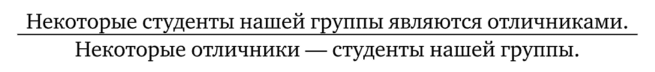 Е —> Е. Общеотрицательное суждение обращается в общеотрицательное: 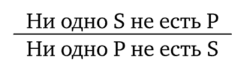 Например, 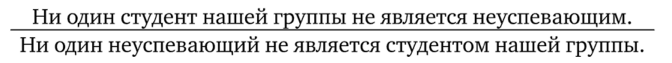 Частноотрицательное суждение О не обращается. 3. Противопоставление предикату — вид непосредственного умозаключения, когда сначала выполняется операция превращения, а затем — обращения, то есть превращение посылки и обращение вывода. Превращение: 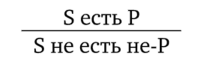 Обращение: 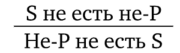 Схема противопоставления предикату: 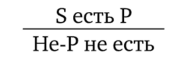 или или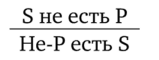 В результате субъектом заключения становится понятие, противоречащее предикату посылки, а предикатом — субъект посылки. Противопоставлению предикату подлежат суждения А, Е, О. А —» Е (А —> Е — превращение, затем Е —> Е — обращение). Общеутвердительное суждение этим способом преобразуется в общеотрицательное:  Например,  Е —> I (Е —> А — превращение, затем А —»I — обращение). Общеотрицательное суждение преобразуется в частноутвердительное:  Например,  О —^ I (О —^ I — превращение, затем I —> I — обращение). Частноотрицательное суждение преобразуется в частноутвердительное:  Например,  Частноутвердительное суждение I посредством противопоставления предикату не преобразуется. 4. Противопоставление субъекту — вид непосредственного умозаключения, когда сначала выполняется операция обращения, а затем превращения, то есть обращение посылки и превращение вывода. Обращение:  Превращение: 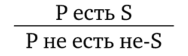 Схема противопоставления субъекту: 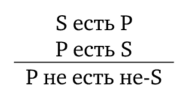 или или Противопоставлению субъекту подлежат суждения А, Е, I. А —> О (А I — обращение, затем I —> О — превращение). Общеутвердительное суждение преобразуется этим способом в частноотрицательное:  Например,  Е —» А (Е —>Е — обращение, Е —> А — превращение). Общеотрицательное суждение преобразуется в общеутвердительное:  Например,  I —> 0(1 —> I — обращение, затем I —> О — превращение). Частноутвердительное суждение преобразуется в частноотрицательное:  Например,  Частноотрицательное суждение О посредством противопоставления субъекту не преобразуется. 5. Умозаключения по логическому квадрату. Логический квадрат — фигура для запоминания отношений между суждениями А, Е, I, О. Логический квадрат был предложен в XI веке византийским богословом и логиком Михаилом Пселлом (рис. 32). По углам квадрата располагаются суждения А, Е, I, О, а его стороны и диагонали символически выражают основные логические отношения между суждениями. 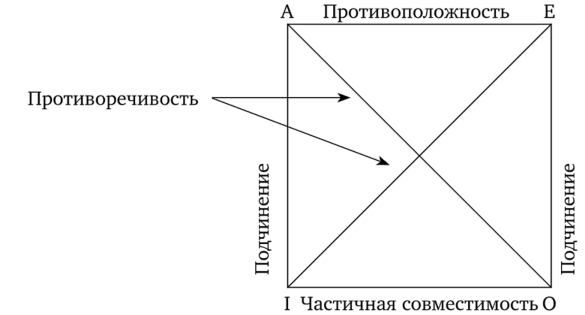 Рис. 32 Между суждениями А, I, Е, О существуют четыре вида отношений. 1. Отношение подчинения (А — I, Е — О). Суждения А, Е — подчиняющие, суждения I, О — подчиненные. Если общее суждение истинно, то истинным является и частное суждение. Например, если истинно суждение «Все воскресные дни — выходные» (А), то суждение «Некоторые воскресные дни — выходные» (I) также будет истинным. 2. Отношение противоречивости (контрадикторности) (А — О, Е — I) между суждениями, которые относятся друг к другу как отрицание одним другого. Если одно из суждений истинно, то другое обязательно ложно. Оба суждения не могут быть одновременно ни истинными, ни ложными. Например, зная, что суждение «Ни один житель Уганды не был на Луне» (Е) является истинным, заключаем, что противоречивое ему суждение «Некоторые жители Уганды были на Луне» (I) — ложно. 3. Отношение противоположности (контрарности) (А — Е) предполагает, что данные суждения не могут одновременно быть истинными, но могут одновременно быть ложными. Таким образом, если одно из суждений данной пары истинно, то другое — обязательно ложно. Например, суждения «Все люди любят джаз» (А) — «Ни один человек не любит джаз» (Е) очевидно ложны. 4. Отношение частичной совместимости (субконтрарности) (I — О) характеризуется тем, что эти суждения могут оба быть истинными, но не могут оба быть ложными. Например, оба суждения «Некоторые птицы летают» (I) и «Некоторые птицы не летают» (О) являются истинными. Перечисленные отношения между суждениями можно представить в виде таблицы (табл. 11). Таблица 11
Отсюда правомерны следующие выводы: Отношение подчинения: А —» I, Е —» О, I —»А, О —>Е; Отношение противоречивости: А—>0, А—>0, Е—>1,Е—>1; Отношение противоположности: А —> Е, Е —> А; Отношение частичной совместимости: I —>О, О—>1. Отрицание производится путем применения связки «неверно, что» перед соответствующими простыми суждениями. 21.Простой категорический силлогизм. Состав силлогизма. Состав простого категорического силлогизма Широко распространенным видом опосредованных умозаключений является простой категорический силлогизм, заключение в котором получается из двух категорических суждений. Например, из суждений: 1) «Обвиняемый (S) имеет право на защиту (Р)» и 2) «Иванов (S) – обвиняемый» следует заключение 3) «Иванов (S) имеет право на защиту (Р)», которое также представляет собой категорическое суждение. Таким образом, простой категорический силлогизм состоит из трех категорических суждений, два из которых являются посылками, а третье – заключением. Расчленим суждения, из которых состоит силлогизм, на понятия. Этих понятий три, причем каждое из них входит в состав двух суждений «Обвиняемый» – в 1–ю посылку как субъект и во 2–ю посылку как предикат; «имеет право на защиту» – в 1–ю посылку и в заключение как их предикаты; «Иванов» – во 2–ю посылку и в заключение как их субъекты. В отличие от терминов суждения – субъекта (S) и предиката (Р) – понятия, входящие в состав силлогизма, называют терминами силлогизма. Различают меньший (это понятие, которое в заключении является субъектом), больший (понятие, которое в заключении является предикатом), средний (понятие, входящее в обе посылки и отсутствующее в заключении). Меньший и больший термины называются крайними и обозначаются соответственно латинскими буквами S (меньший термин) и Р (больший термин). Каждый из крайних терминов входит не только в заключение, но и в одну из посылок. Посылка, в которую входит меньший термин, называется меньшей посылкой, в которую входит больший термин – большей посылкой. Для удобства анализа силлогизма посылки принято располагать в определенной последовательности: большую – на первом месте, меньшую – на втором. Под чертой записывают заключение: Обвиняемый имеет право на защиту. Иванов – обвиняемый. Иванов имеет право на защиту. Однако в рассуждении такой порядок необязателен. Меньшая посылка может находиться на первом месте, большая – на втором. Иногда посылки могут стоять и после заключения. Посылки различаются не их местом в силлогизме, а входящими в них терминами. Вывод в силлогизме был бы невозможен, если бы в нем не было бы среднего термина. Данный термин обозначается латинской буквой М. Средний термин связывает два крайних термина. Отношение крайних терминов (субъекта и предиката) устанавливается благодаря их отношению к среднему термину. В самом деле, из большей посылки нам известно отношение большего термина к среднему термину. Зная отношение крайних терминов к среднему, мы можем установить отношение между крайними терминами. Таким образом, вывод из посылок оказывается возможным потому, что средний термин выполняет роль связующего звена между двумя крайними терминами силлогизма. Поставив в нашем примере на место терминов суждения термины силлогизма, получим: Обвиняемый (М) имеет право на защиту (Р). Иванов (S) – обвиняемый (М). Иванов (S) имеет право на защиту (Р). Простой категорический силлогизм – это умозаключение об отношении двух крайних терминов на основании их отношения к среднему термину. Правомерность вывода, т.е. логического перехода от посылок к заключению, в категорическом силлогизме основывается на положении (аксиоме силлогизма): все, что утверждается или отрицается относительно всех предметов некоторого класса, утверждается или отрицается относительно каждого предмета и любой части предметов этого класса. В данном примере – все, что утверждается относительно всех обвиняемых, утверждается и относительно конкретного обвиняемого. |
