логика. ответы к экзамену логика. Логика наука о мышлении, ее предметом, являются законы и формы, приемы и операции мышления, с помощью которых человек познает окружающий его мир

• Название: Логика наука о мышлении, ее предметом, являются законы и формы, приемы и операции мышления, с помощью которых человек познает окружающий его мир
• Анкор: логика
• Дата: 25.01.2022
• Размер: 2.69 Mb.
• Имя файла: ответы к экзамену логика.docx
• Тип: Вопросы к экзамену; #341670
• страница: 6 из 7

Неполной индукцией называют умозаключение, которое на основе наличия определенных повторяющихся признаков причисляет тот или иной предмет к классу однородных ему предметов, также имеющих такой признак.

Неполная индукция часто применяется в повседневной жизни человека и научной деятельности, так как позволяет делать заключение на основе анализа определенной части данного класса предметов, экономит время и силы человека. При этом нельзя забывать, что в результате неполной индукции получается вероятностное заключение, которое в зависимости от вида неполной индукции будет колебаться от менее вероятного к более вероятному^{11}.

Схему неполной индукции можно представить как:

S1 — Р

S2 — Р

S3 — Р

S1, S2, S3… составляют класс К.

Вероятно, каждый элемент К — Р.

Сказанное выше можно проиллюстрировать следующим примером.

Слово «молоко» изменяется по падежам. Слово «библиотека» изменяется по падежам. Слово «врач» изменяется по падежам. Слово «чернила» изменяется по падежам.

Слова «молоко», «библиотека», «врач», «чернила» — существительные.

Вероятно, все имена существительные изменяются по падежам.

В зависимости от того, как обосновывается вывод умозаключения, принято делить неполную индукцию на два вида — популярную и научную.

Популярная неполная индукция, или индукция через простое перечисление, рассматривает предметы и классы, к которым эти предметы относятся, не очень глубоко. Так, на основе повторяемости одного и того же признака у некоторой части однородных предметов и при отсутствии противоречащего случая делается общее заключение, что все предметы этого рода обладают этим признаком.

Как видно из названия, популярная индукция очень распространена, особенно в ненаучной среде. Степень вероятности такой индукции невелика.

При формировании популярного индуктивного умозаключения следует помнить о возможных ошибках и не допускать их появления.

Поспешное обобщение означает, что при заключении во внимание принята только та часть фактов, которая говорит в пользу сделанного заключения. Остальные не рассматриваются вовсе.

Например:

Зимой в Тюмени холодно.

Зимой в Уренгое холодно.

Тюмень и Уренгой города.

Во всех городах зимой холодно.

После, значит, по причине — означает, что какое-либо событие, явление, факт, предшествующий рассматриваемому, принимается за его причину.

Подмена условного безусловным означает, что не учитывается относительность любой истины. То есть факты в данном случае могут вырываться из контекста, меняться местами и т. д. При этом продолжает утверждаться истина полученных результатов.

Научная индукция, или индукция через анализ фактов, представляет собой умозаключение, в посылках которого наряду с повторяемостью признака у некоторых явлений класса содержится также информация о зависимости этого признака от определенных свойств явления.

То есть в отличие от популярной индукции научная не ограничивается простой констатацией. Рассматриваемый предмет подвергается глубокому исследованию. В научной индукции очень важно соблюдать ряд требований:

1) предметы исследования должны отбираться планомерно и рационально;

2) необходимо как можно глубже познать природу рассматриваемых предметов;

3) уяснять характерные признаки предметов и их связей;

4) сравнивать результаты с закрепленными ранее научными сведениями.

Важной чертой научной индукции, определяющей ее роль в науке, является способность раскрывать не только обобщенные знания, но и причинные связи. Именно при помощи научной индукции были открыты многие научные законы.

28.Умозаключение по аналогии и его виды.

Термин «аналогия» означает сходство двух предметов²² (или двух групп предметов) в каких-либо свойствах или отношениях. Умозаключение по аналогии — один из самых древних видов умозаключения, присущий человеческому мышлению с самых ранних ступеней развития.

Аналогия — умозаключение о принадлежности предмету определенного признака (т. е. свойства или отношения) на основе сходства в признаках с другим предметом. В форме такого умозаключения осуществляется приписывание предмету свойства или перенос отношений.

Посредством аналогии осуществляется перенос информации с одного предмета (модели) на другой (прототип). Посылки относятся к модели, заключение — к прототипу. В аналогии между Землей (модель) и Марсом (прототип), зная, что на Земле существует жизнь, делаем вывод о том, что и на Марсе, вероятно, есть жизнь.

В зависимости от характера информации, переносимой с од­ного предмета на другой (с модели на прототип), аналогия делится на два вида: аналогия свойств и аналогия отношений.

В аналогии свойств рассматриваются два единичных предмета

(или два множества однородных предметов, два класса), а пере­носимыми признаками являются свойства этих предметов. Схема аналогии свойств в традиционной логике такова:

Предмет А обладает свойствами а, b, с, d, e,f.

Предмет В обладает свойствами а, b, с, d.

___________________________________________

Вероятно, предмет В обладает свойствами е, f.

Примером аналогии свойств может служить аналогия симп­томов протекания той или иной болезни у двух разных людей (два единичных предмета) или у двух групп людей (например, взрослых и детей). Исходя из сходства признаков болезни (симп­томов), врач ставит диагноз.

Аналогия свойств двух предметов иногда дает не только правдоподобное, но даже достоверное заключение. Например, обнаружено, что геологическая структура Южно-Африканского плоскогорья имеет много общего с геологической структурой Восточно-Сибирской платформы. В алмазных жилах Южной Африки находили голубоватый минерал. Случайно обнаружили такой же голубоватый минерал в устье одной из речек Якутии. Сделали по аналогии заключение, что, вероятно, и в Якутии есть месторождение алмазов. Это заключение подтвердилось. Теперь в Якутии осуществляется промышленная добыча алмазов²³.

В аналогии отношений информация, переносимая с модели на прототип, характеризует отношения между двумя предметами. Пусть имеется отношение (aRb) и отношение (mR₁n).Сходными, аналогичными выступают отношения R и R₁, но а не аналогично m, а b не аналогично n. Примером является предложенная Резерфордом планетарная модель строения атома, которую он по­строил на основании аналогии отношения между Солнцем и пла­нетами, с одной стороны, и ядром атома и электронами, которые удерживаются на своих орбитах силами притяжения ядра, — с другой. Здесь R — взаимодействие противоположно направлен­ных сил — сил притяжения и отталкивания — между планетами и Солнцем, а R₁— взаимодействие противоположно направлен­ных сил — сил притяжения и отталкивания — между ядром ато­ма и электронами.

Кроме деления на два вида — аналогия свойств и аналогия отношений — по характеру выводного знания (по степени достове­рности заключения) умозаключения по аналогии можно разделить на три вида: 1) строгая аналогия, дающая достоверное заключе­ние; 2) нестрогая аналогия, дающая вероятное заключение; 3) ложная (вульгарная) аналогия, дающая ложное заключение.

Строгая аналогия

Характерным признаком, отличающим строгую аналогию от нестрогой и ложной, является наличие необходимой связи общих признаков с переносимым признаком. Схема строгой аналогии такова:

Предмет А обладает признаками а, b, с, d, e.

Предмет В обладает признаками а, b, с, d.

Из совокупности признаков а, b, с, d необходимо следует е.

______________________________________________

Предмет В обязательно обладает признаком е.

Если из совокупности признаков М={а, b, с, d} закономерно, необходимо следует признак е, то эту зависимость можно запи­сать так:



(Здесь — знак вывода.) Структура строгой аналогии подобна структуре правилаmodus ponens условно-категорического умозаключения и поэтому дает достоверный, а не правдоподоб­ный вывод.

Строгая аналогия применяется в научных исследованиях, в математических доказательствах. Так, например, формулиров­ка признаков подобия треугольников основана на строгой анало­гии. «Если три утла одного треугольника равны трем углам другого треугольника, то эти треугольники подобны» (подо­бие — вид аналогии).

На свойствах умозаключения по строгой аналогии основан метод моделирования. Научные аналогии позволяют использо­вать имеющийся к настоящему времени опыт, при этом кроме формально-логических принципов проведения аналогий необхо­димо учитывать и методологическое требование конкретности истины, рассмотрения явления в конкретно-исторической обста­новке.

При овладении управляемой термоядерной реакцией и созда­нии термоядерной энергетики люди получат практически неог­раниченные топливные ресурсы. В природе высокотемпературная плазма в естественном виде существует в атмосфере звезд. «Для управляемого термоядерного синтеза необходимо необычное в земных условиях солнечное вещество — водородная плазма с температурой около ста миллионов градусов. На Солнце она удерживается гравитационным полем, а на Земле ее можно дер­жать в повиновении магнитным полем. Но ведь по воздействию на частицы плазмы магнитное поле совершенно не похоже на гравитационное...»²⁴

Ученые нашей страны предложили способ решения этой про­блемы. Созданная ими теория равновесия и устойчивости плаз­мы уже используется при проектировании термоядерных устано­вок.

Нестрогая аналогия

В отличие от строгой аналогии нестрогая аналогия дает не достоверное, а лишь вероятное заключение. Если ложное сужде­ние обозначить через 0, а истину — через 1, то степень вероят­ности заключений по нестрогой аналогии лежит в интервале от 1 до 0, т. е. 1>Р(а)>0, где Р (а) — обозначение вероятности заключения по нестрогой аналогии.

Примерами нестрогой аналогии являются, в частности, следу­ющие: испытание модели корабля в бассейне и заключение о том, что настоящий корабль будет обладать теми же характеристи­ками, испытание прочности моста на модели, затем построение настоящего моста. При строгом выполнении всех правил постро­ения и испытания модели этот способ умозаключения может приближаться к строгой аналогии и давать достоверное заключе­ние, однако чаще заключение бывает вероятным. Разница в мас­штабах, между моделью и прототипом (самим сооружением) иногда бывает не только количественной, но и качественной. Так же не всегда можно учесть различие между лабораторными условиями испытания модели и естественными условиями рабо­ты самого сооружения, в результате чего возникают ошибки.

Для повышения степени вероятности заключений по нестро­гой аналогии следует выполнить ряд условий:

1) число общих признаков должно быть возможно большим;

2) сходные признаки должны быть существенными. Аналогия на основе сходства несущественных признаков типична для ненауч­ного и детского мышления. Например, дети могут съесть ядови­тые ягоды на основе их внешнего сходства со съедобными;

3) общие признаки должны быть по возможности более раз­нородными; 4) необходимо учитывать количество и существен­ность пунктов различия. Если предметы различаются в сущест­венных признаках, то заключение по аналогии может оказаться ложным; 5) переносимый признак должен быть того же типа, что и сходные признаки.

Ложная аналогия

При нарушении указанных выше правил аналогия может дать ложное заключение, т. е. стать ложной. Вероятность заключения по ложной аналогии равна 0 (Р (а) = 0). Ложные аналогии иногда делаются умышленно, с целью ввести противника в заблуждение, и тогда они являются софистическим приемом, в других случаях они делаются случайно, в результате незнания правил постро­ения аналогий или отсутствия фактических знаний относительно предметов А и В и их свойств, на основании которых осуществля­ется аналогия.

Подобную ошибку совершали в XIX в. сторонники вульгар­ного материализма Л. Бюхнер, К. Фохт и Я. Молешотт, которые, проводя аналогию между печенью и мозгом, утверждали, что мозг выделяет мысль так же, как печень выделяет желчь.

Обобщим сказанное о строгой, нестрогой и ложной аналоги­ях. Если Р (а)=1, т. е. заключение получается достоверным, то это будет строгая аналогия. Если 1 > Р (а) > 0, т. е. заключение будет вероятным, то это будет нестрогая аналогия. Если Р (а) = 0, т. е. заключение — ложное суждение, то это будет ложная анало­гия.

Итак, рассмотрены три вида аналогии в зависимости от хара­ктера выводного знания, т. е. по степени достоверности заключе­ния: получено истинное заключение, определенная степень веро­ятности заключения или ложное заключение. Вероятностные за­ключения тем ценнее, чем их вероятность ближе к 1 (истине).

Мы полагаем, что это деление на три вида в зависимости от степени достоверности заключения можно проследить и на ин­дуктивных умозаключениях, а позднее, в теме «Гипотеза», — и на гипотезах.

В теме «Гипотеза» мы увидим, что существуют гипотезы, превращающиеся в научную теорию, вероятность такой гипотезы равна 1; степень вероятности других гипотез 1 >Р (a)>0; вероят­ность ложных гипотез, которые являются ложными суждениями или ложными теоретическими построениями, равна 0 (т. е. P(а) = 0).
29.Структура доказательства и его виды.

Доказательство - это совокупность логических приемов обоснования истинности какого-либо суждения с помощью связанных с ним суждений, истинность которых уже установлена.
       Различают два способа установления истинности суждения: непосредственный и опосредованный.
       Непосредственный способ (эмпирическое доказательство) основан на эмпирических процедурах (наблюдение, эксперимент, измерение и т.д.)
       Опосредованный (логическое доказательство) основан на логических формах. Состоит в установлении необходимой логической связи доказываемого утверждения с положениями, истинность которых считается установленной.

       В структуру доказательства входят следующие основные элементы:
       1)тезис - доказываемое положение,
       2)аргументы(основания) - утверждения, при помощи которых обосновывается истинность тезиса ,
       3)демонстрация (форма) - логическая связь тезиса с аргументами.

       Тезис доказательства - суждение, которое подлежит обоснованию. В дедуктивных науках тезис называется теоремой.
       Поскольку аргументы суть истинные утверждения, с помощью которых определяют истинность тезиса, в обыденном языке их называют "доказательствами". В формальных доказательствах употребляются термины "посылки", или "основания".

Виды доказательств

Различают прямые и косвенные доказательства.
       Прямое доказательство - это доказательство, в котором тезис необходимо следует из аргументов (не нужно прибегать к помощи каких-либо дополнительных построений).
        Модус поненс и модус Barbara (ААА) самые распространенные формы прямого доказательства. Прямое доказательство, как правило, наиболее эффектно и красиво
        Косвенное доказательство - доказательство, в котором истинность тезиса устанавливается через доказательство ложности противоречащего ему антитезиса
        Выделяют два вида косвенных доказательств апагогические и разделительные косвенные доказательства.
        Апагогическое косвенное доказательство (греч. apagoge - вывод; apagogos - уводящий, отводящий) косвенное доказательство ("приведение к абсурду") состоит в том, что мы начинаем выводить из антитезиса следствия и показываем, что некоторые из этих следствий (хотя бы одно) явно противоречат известным истинным положениям. Таким образом, принятие антитезиса ведет к противоречию (к абсурду), поэтому его следует признать ложным. Но тогда тезис необходимо признать истинным.

Разделительное косвенное доказательство состоит в построении разделительного суждения, элементами которого являются доказываемый тезис и некоторые несовместимые с ним утверждения (так сказать, антитезисы). Затем показывают, что за исключением тезиса все элементы разделительного суждения ложны. Следовательно, нужно признать тезис истинным - это любимая схема рассуждения всех сыщиков и следователей, ибо это не что иное как известная нам схема модуса толлендо-поненс разделительно-категорического силлогизма.

30.Правила доказательства. Ошибки в доказательствах.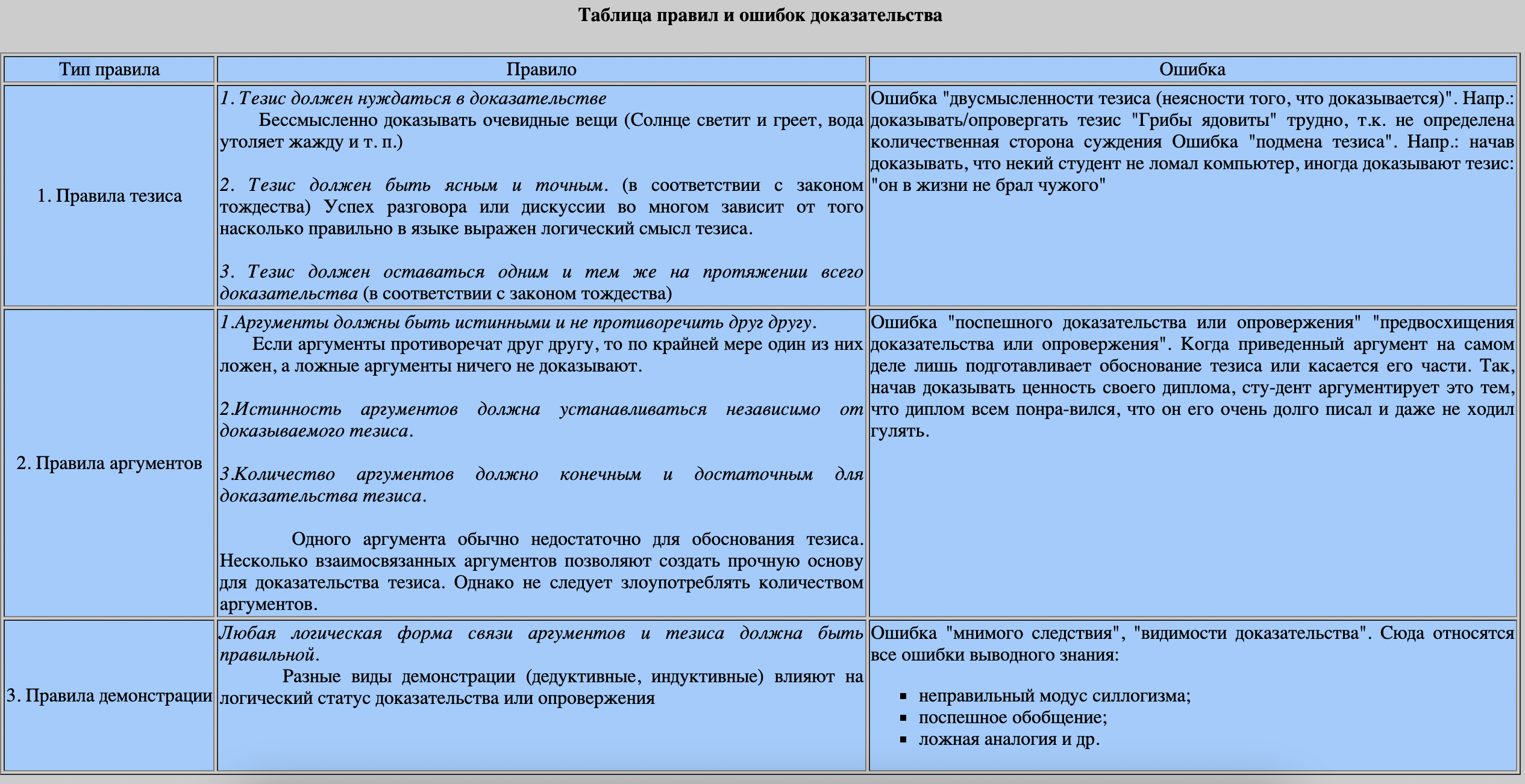



В качестве аргументов в доказательстве могут использоваться:

• 
  констатации фактов, истинность которых обосновывается опытом и наблюдением, например, "Огонь жжет", "Река Волга впадает в Каспийское море", "У подосиновиков красные шляпки" и т. п.;
  
• 
  определения понятий, представляющие собой соглашения о смысле употребляемых терминов, например: "Окружность есть кривая замкнутая линия, равно удаленная от некоторой точки", "Геном называют простейшую единицу наследственности", "Слово "месяц" в русском языке имеет то же значение, что и слово "Луна" и т. п.;
  
• 
  аксиомы, или постулаты, той области знания, в рамках которой проводится доказательство, например, если вы доказываете теорему в области евклидовой геометрии, вы можете в качестве аргументов использовать известные 5 аксиом Евклида; если речь идет о физике, вы можете опираться на принципы сохранения, законы термодинамики, принципы квантовой механики; в биологии - на естественный отбор Дарвина и законы Менделя и т. п.;
  
• 
  наконец, в качестве аргументов можно использовать и ранее доказанные положения: если в ходе ваших рассуждений вы доказали какой-то тезис, то в дальнейшем этот тезис можно использовать как аргумент для доказательства других положений.