ТАУ КП БОНЧ ВЕРХОВА. ТАУ КП. М. А. БончБруевича институт непрерывного образования (ино) Дисциплина Теория автоматического управления Пояснительная записка
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
 САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ (ИНО) Дисциплина: «Теория автоматического управления» Пояснительная записка К курсовому проекту Выполнил: Группа №: Студ. билет № Вариант 8 Проверил: Санкт-Петербург 2022 СодержаниеСАНКТ-ПЕТЕРБУРГСКИЙ 1 ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ 1 им. проф. М.А. Бонч-Бруевича 1 ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ (ИНО) 1 Группа №: 1 Студ. билет № 1 Вариант 8 1 Санкт-Петербург 1 2022 1 Содержание 2 Введение 3 Исходные данные 5 1.Уравнения звеньев 6 2.Приведение системы уравнений по звеньям к единому дифференциальному уравнению 11 3.Передаточная функция замкнутой системы и её разомкнутой цепи 12 4. Получение уравнения статики системы и его использование при расчете системы 13 5. Проверка системы на устойчивость по критерию Вышнеградского 14 6. Проверка САУ на устойчивость по методу Рауса 17 7. Проверка САУ на устойчивость по методу Гурвица 19 8. Проверка САУ на устойчивость по методу Михайлова 21 Выводы 23 Литература 24 ВведениеТеория автоматического управления (ТАУ) является базовой основой кибернетики или науки об управлении – одной из относительно молодых областей науки. Теория управления, хотя и прошла яркий путь своего развития, но в настоящее время продолжает интенсивно развиваться в сторону создания теории интеллектуальных систем управления – предельной формации парадигмы теории управления. Прикладную или инженерную ТАУ сегодня именуют «классической», подчеркивая этим определенную завершенность форм ее развития как науки об управлении. Классическая ТАУ, преследуя цель «оптимизации в малом», решает задачи оптимизации и адаптации при малых отклонениях относительно заданного режима работы системы управления. Основы «современной» ТАУ идеологически заложены в «классической» ТАУ и составляют с ней неразрывную связь. Современная ТАУ, преследуя цель «оптимизации в целом», применительно, в основном, к системно-сложным ОУ, превращается в совокупность методов и средств, осуществляющих эффективное использование всех ресурсов системы при многокритериальной интеллектуальное управление и составляющих основу теории интеллектуальных систем управления. Характерной обобщающей чертой последних является максимально оптимизации процессов в целом в условиях, как правило, частичной неопределенности информации о свойствах ОУ и среде его функционирования. Теория автоматического управления (ТАУ) относится к классу важнейших общеспециальных дисциплин, входящих во все типовые программы инженерного образования, ТАУ изучает процессы управления, методы исследования и основы проектирования систем автоматического управления (САУ). ТАУ изучает принципы построения САУ, закономерности протекающих в них процессов в целях построения работоспособных и точных САУ. Методами ТАУ осуществляются анализ и синтез САУ. В данном курсовом проекте решаются задачи, связанные с анализом и синтезом САУ, относящиеся к «классической» ТАУ. Исходными данными для выполнения курсового проекта являются структурная схема замкнутой автоматической системы регулирования и параметры входящих в нее звеньев. Исходные данные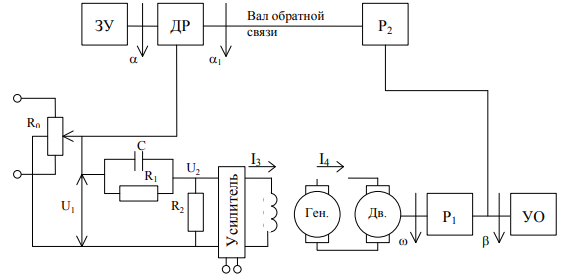 Рис. 1 – Следящая система Принципиальная схема масштабной следящей системы изображена на рис. 1. Система предназначена для слежения в постоянном масштабе вала управляемого объекта за задающим валом. Как показано на рис. 1, механический дифференциал, выполняющий функцию датчика рассогласования, сравнивает углы поворота вала задающего устройства α и вала обратной связи α1. Полученное рассогласование γ = α - α1 с помощью потенциометра преобразуется в напряжение U1 которое подается на вход дифференцирующего контура, состоящего из емкости С и сопротивлений R1 и R2. Усиленный усилителем ток I3 поступает на обмотку возбуждения генератора, цепь якоря которого последовательно соединена с цепью якоря двигателя постоянного тока с независимым возбуждением. Двигатель через редуктор Р1 поворачивает вал управляемого объекта на угол β = K0·α. Так как датчик рассогласования должен сравнивать величины одного масштаба, в цепь обратной связи включен редуктор Р2, задачей которого является изменение масштаба угла β в 1.Уравнения звеньев1. Уравнение управляемого объекта с двигателем. Уравнение имеет вид: где I - приведенный к валу объекта момент инерции всех масс, связанных с этим валом; МВР - вращающийся момент на валу объекта; Мт - момент сил трения и сопротивления; Мнг - момент внешней нагрузки на объект. Принимаем: где I4 - ток в цепи якоря двигателя, 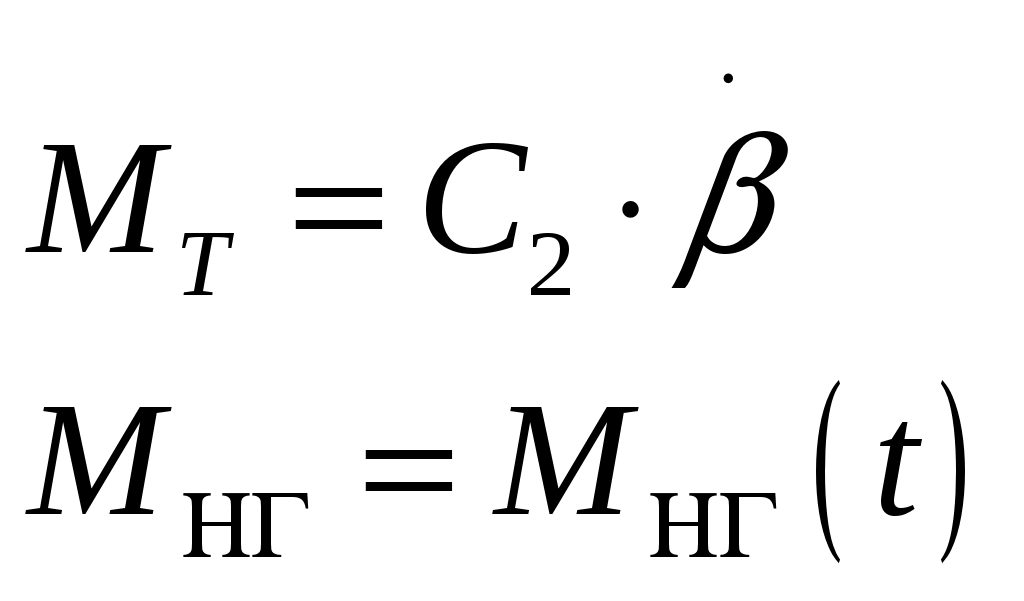 Уравнение управляемого объекта с двигателем в стандартной форме принимает вид Где 2. Уравнение обратной связи 3. Уравнение датчика рассогласования 4. Уравнение потенциометра 5. Уравнение дифференцирующего контура Где Полезный сигнал дифференцирующего контура характеризуется правой частью уравнения Постоянная времени Т2 определяет методическую ошибку при дифференцировании. Для уменьшения методической ошибки рекомендуется параметры контура подобрать так, чтобы постоянная Т5 значительно превышала постоянную времени Т2. Для этого рекомендуется придерживаться отношения 6. Уравнение усилителя и цепи возбуждения генератора Напишем уравнение электрической цепи возбуждения генератора и усилителя: где L3 и R3 - индуктивность и сопротивление обмотки возбуждения генератора; Ri - внутреннее сопротивление лампы усилителя, I3 - ток в цепи обмотки возбуждения генератора; q - коэффициент усиления В стандартной форме записи искомое уравнение принимает вид Где 7. Уравнение цепи якорей генератора и двигателя. Уравнение электрической цепи якорей генератора и двигателя может быть записано так: где L4, R4 - индуктивность и сопротивление цепи якорей; I4 - ток в цепи якорей; Ег - ЭДС генератора, Ед - противоЭДС двигателя. Считая, что или учитывая уравнение редуктора 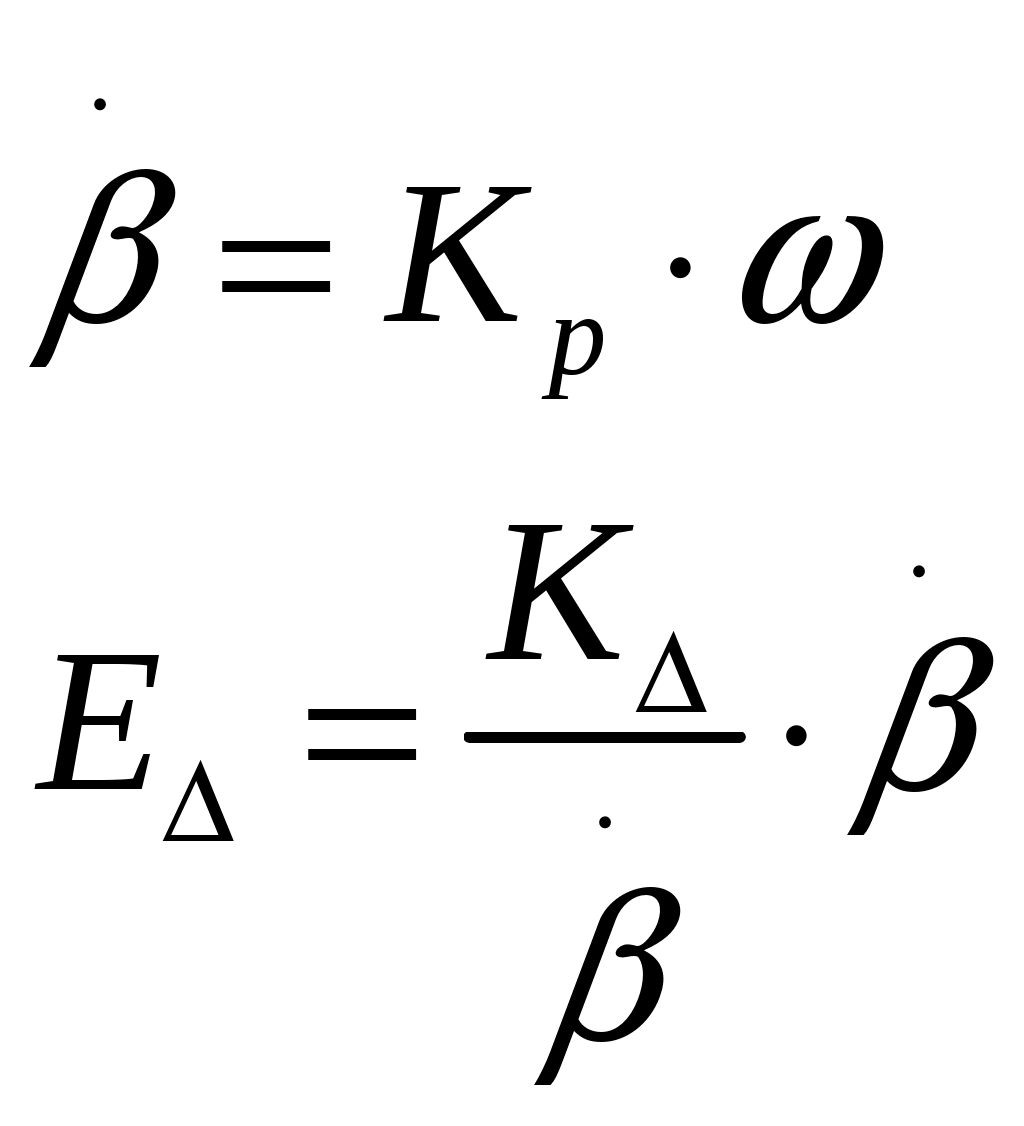 Получим Где ПротивоЭДС двигателя играет роль дополнительной отрицательной обратной связи. Единое уравнение системы получим путем решения системы уравнений звеньев относительно рассогласования γ и задающего воздействия α, при этом Система уравнений имеет вид: 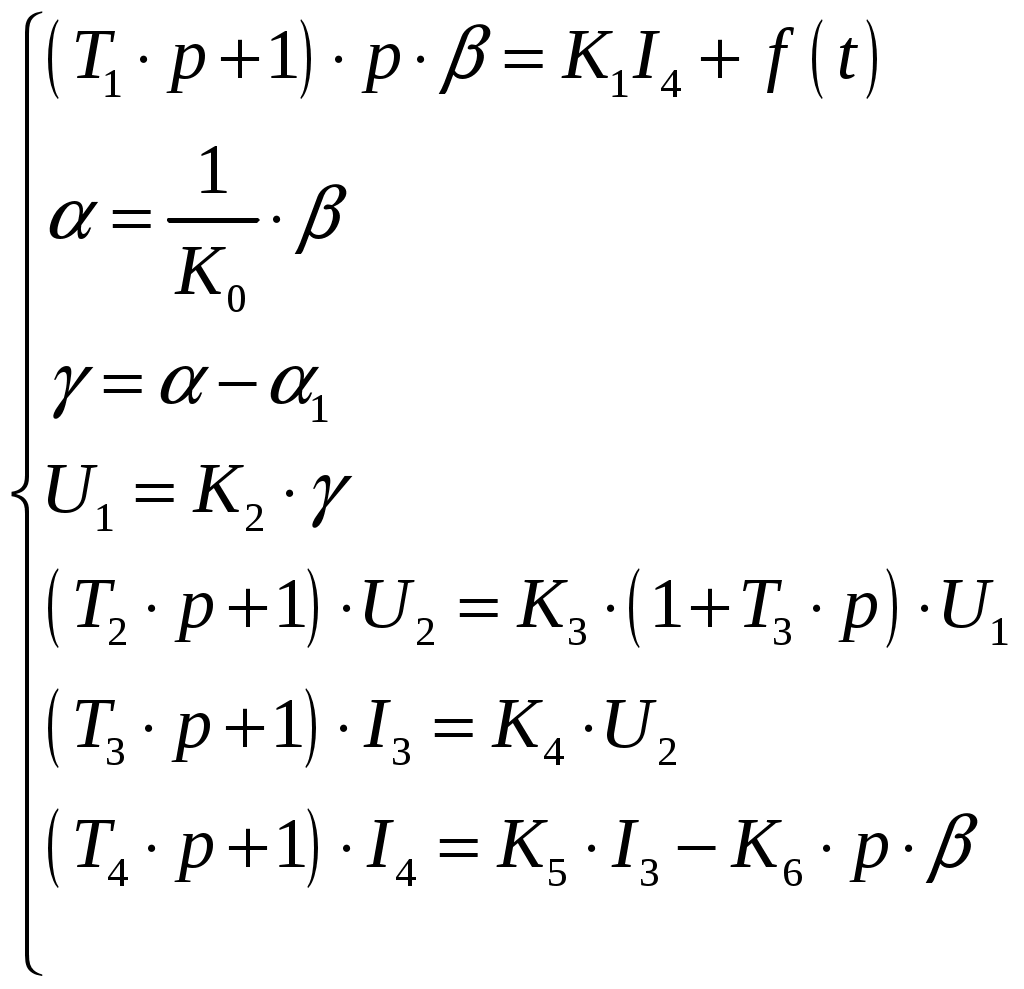 Учитывая, что Получим: 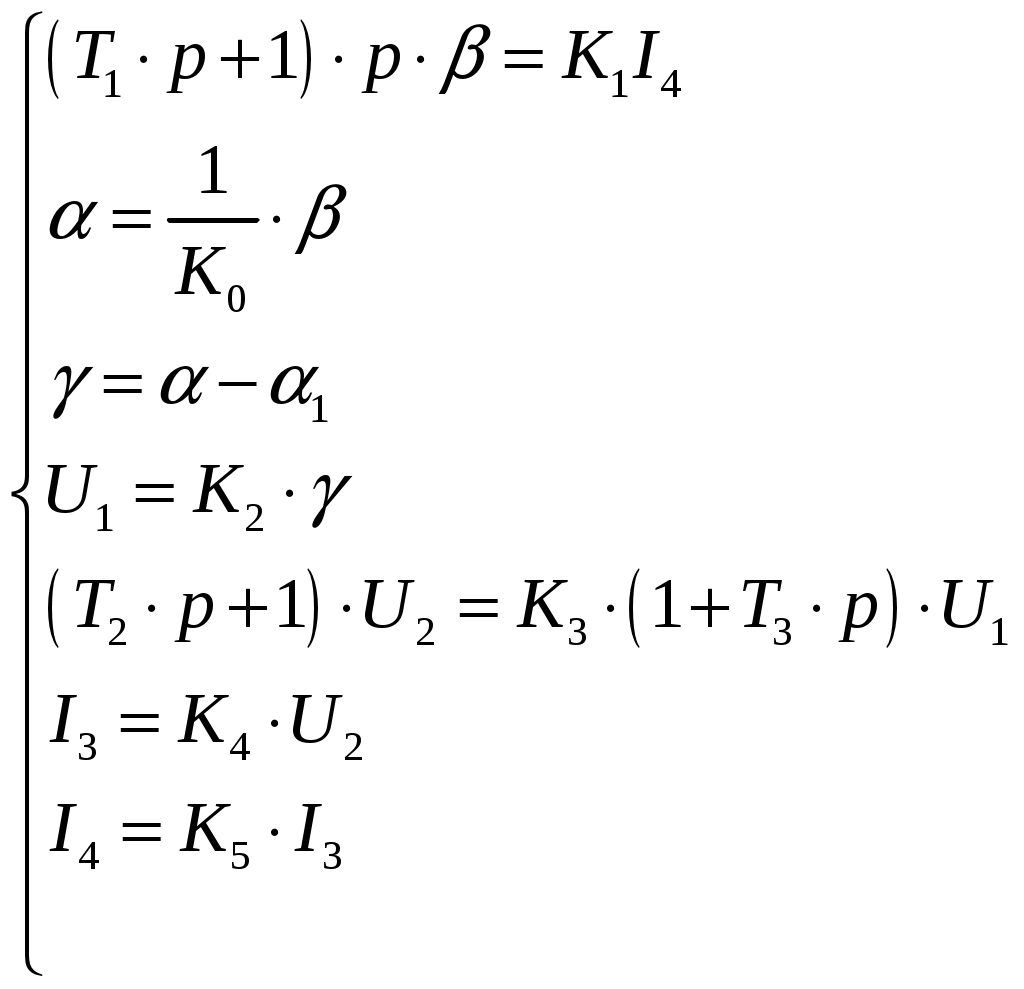 Исходные данные: Неизвестными величинами являются общий коэффициент системы k* = k1·k и параметры дифференцирующего контура. Передаточные функции звеньев системы: 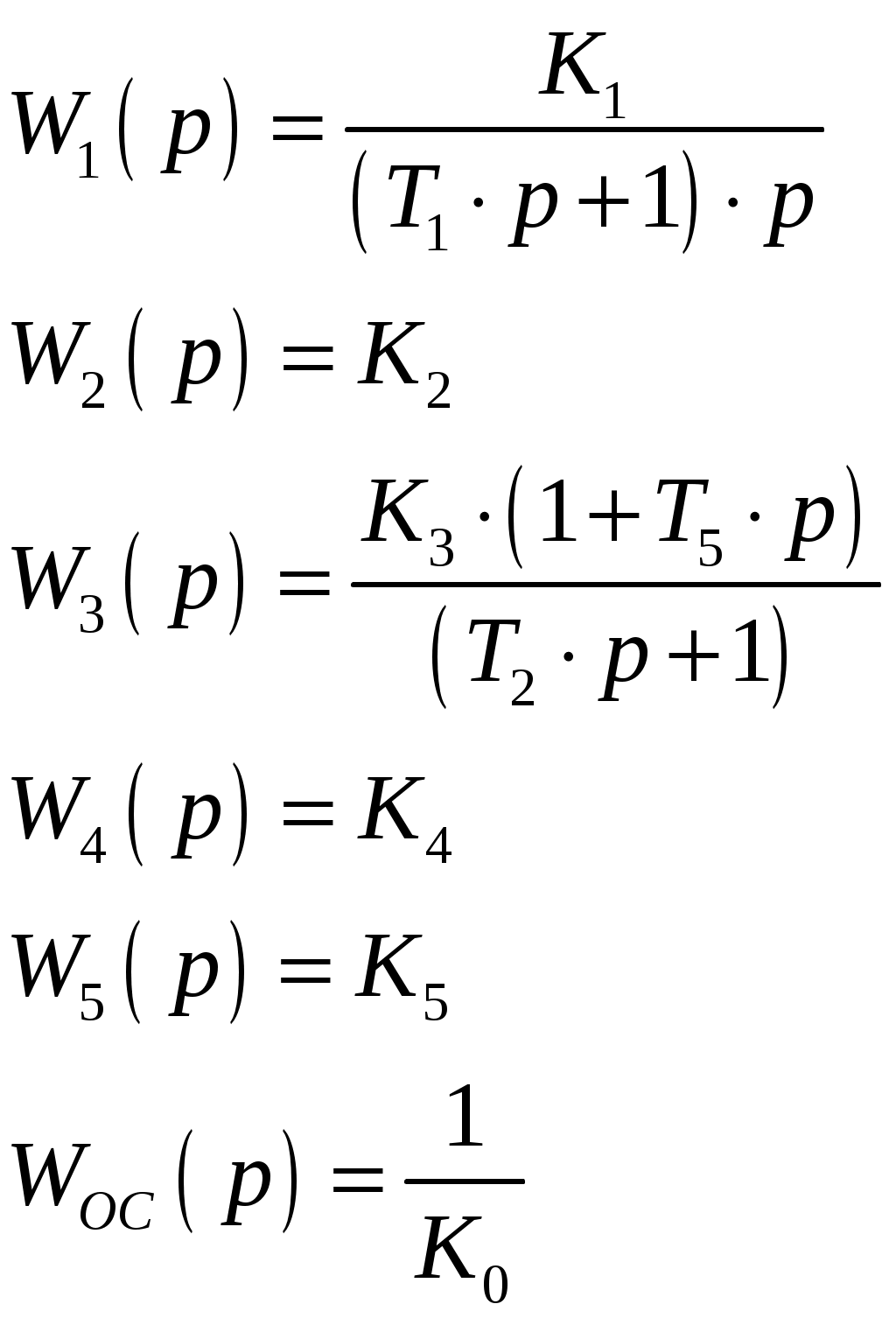 Если в первой части уравнения звена помимо входной величины есть еще и внешнее возмущающее воздействие, такое звено будет иметь помимо основной еще и дополнительную передаточную функцию. Дополнительная передаточная функция представляет собой отношение выходной величины звена к соответствующему воздействию, выраженные в определенной форме через их операторные члены В нашей следящей системе такие воздействия отсутствуют На рис. 2 представлена структурная схема следящей системы 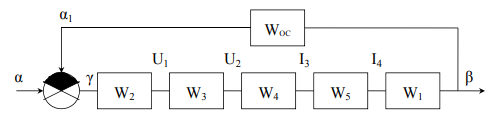 Рис. 2 – Структурная схема следящей системы 2.Приведение системы уравнений по звеньям к единому дифференциальному уравнениюДля того чтобы вывести единое уравнение системы, решим дифференциальные уравнения относительно рассогласования γ и задающего воздействия α. 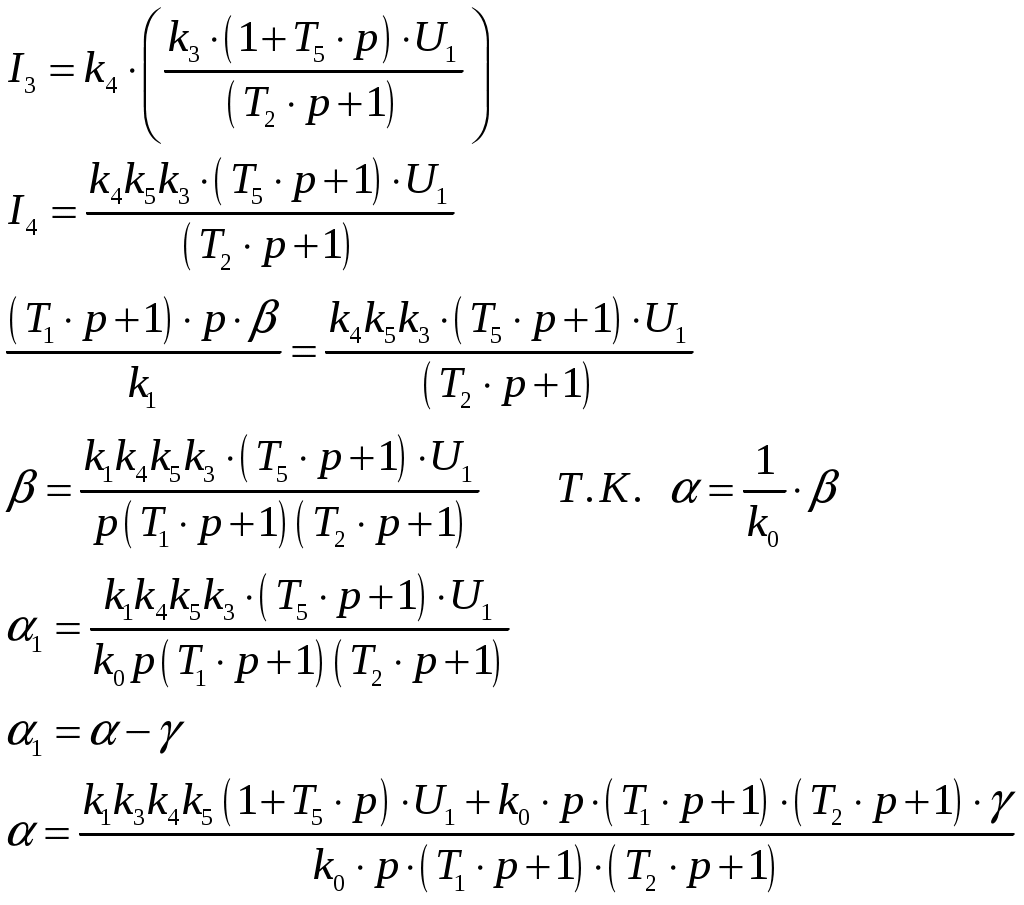 Единое уравнение системы: В (5) k – коэффициент усиления: Уравнение имеет вид: 3.Передаточная функция замкнутой системы и её разомкнутой цепиПередаточная функция замкнутой системы: 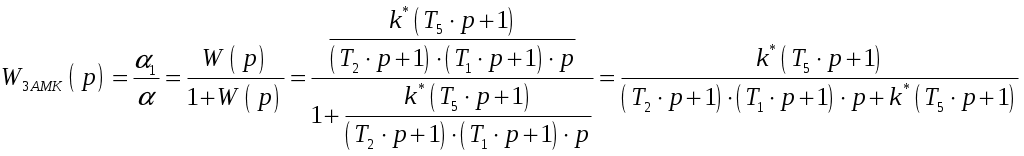 Передаточная функция по ошибке: 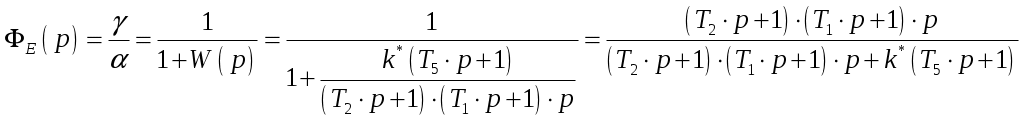 Передаточная функция разомкнутой цепи: 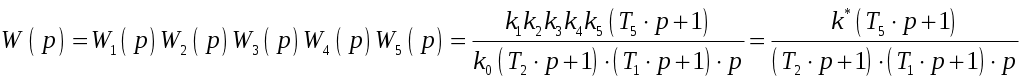 4. Получение уравнения статики системы |
| | | |
| | | |
| | | |
| | - | - |
Все элементы r первого столбца таблицы Рауса имеют один знак - положительны, следовательно, замкнутая система устойчива.
7. Проверка САУ на устойчивость по методу Гурвица
Оцениваем устойчивость замкнутой системы алгебраическим критерием Гурвица. Характеристический полином замкнутой системы:
По необходимому условию Гурвица, все коэффициенты характеристического полинома должны быть положительными. Необходимое условие устойчивости выполняется.
По достаточному условию устойчивости, все определители матрицы Гурвица должны быть положительными. Формируем матрицу Гурвица:
Из коэффициентов характеристического уравнения замкнутой системы
a0pn + a1pn-1 + … + an = 0 составляется таблица, называемая матрицей Гурвица по следующему правилу:
1) по диагонали сверху вниз записываются все коэффициенты, начиная с a1 до an в порядке возрастания индексов;
2) столбцы дополняются вверх коэффициентами с возрастающими индексами, вниз коэффициентами с убывающими индексами;
3) на месте коэффициентов с индексами больше n и меньше нуля проставляются нули.
Матрица Гурвица:
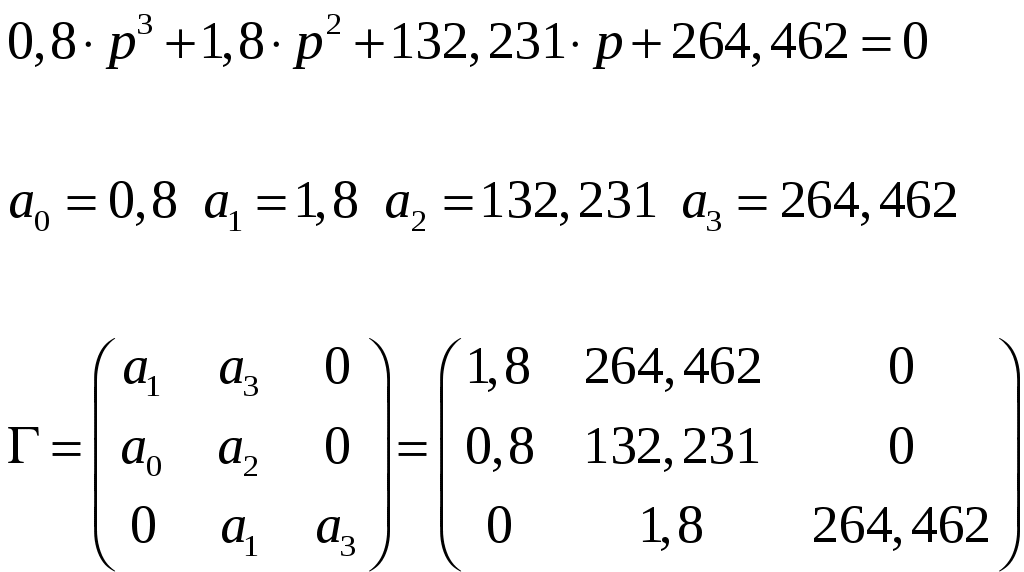
Рассчитываем определители матрицы Гурвица:
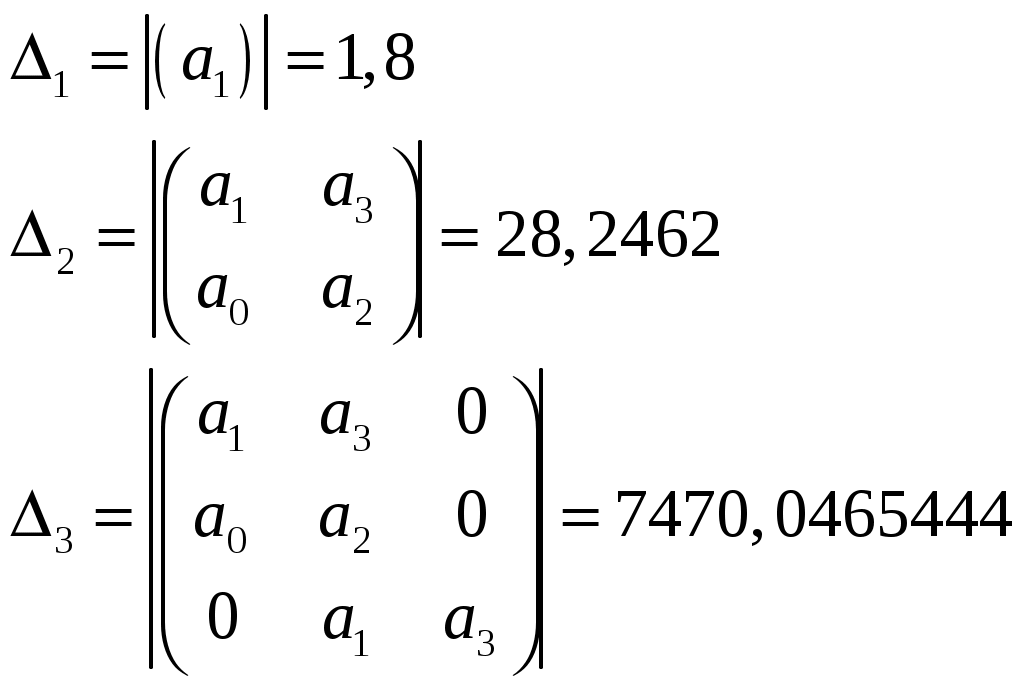
Определители всех 3 порядков матрицы Гурвица положительные, следовательно, замкнутая система устойчива.
8. Проверка САУ на устойчивость по методу Михайлова
Оцениваем устойчивость замкнутой системы частотным критерием Михайлова. Характеристический полином замкнутой системы:
Для того чтобы САУ была устойчивой, необходимо и достаточно, что-
бы кривая Михайлова при изменении частоты от 0 до +∞, начинаясь при
ω = 0 на вещественной положительной полуоси, обходила только против
часовой стрелки последовательно n квадратов координатной плоскости, где
n - порядок характеристического уравнения.
Выполним подстановку p→j·ω в наш характеристический полином:
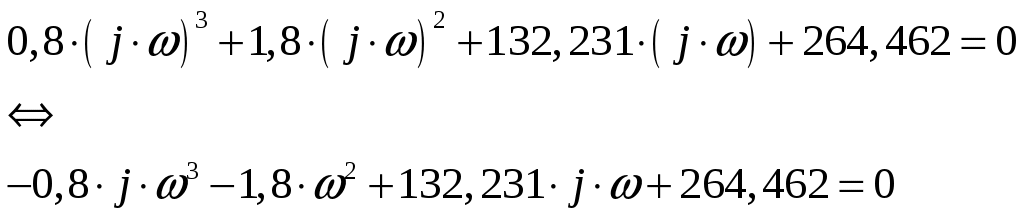
Выделяем действительную и мнимую составляющую:
Заполняем таблицу значений:
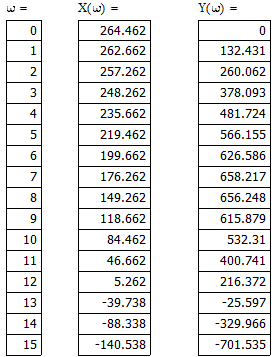
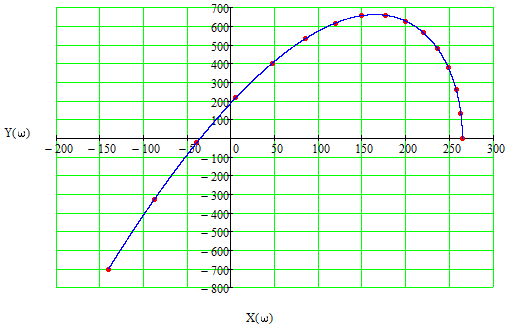
Рис. 4 – Годограф Михайлова замкнутой системы.
Годограф Михайлова при изменении частоты от 0 до +∞, начинаясь при
ω = 0 на вещественной положительной полуоси, обходит против
часовой стрелки последовательно n = 3 квадрата координатной плоскости, что соответствует поведению годографа устойчивой системы
Замкнутая система устойчива.
Выводы
На основании заданной схемы следящей системы составлена структурная схема системы, выделены передаточные функции отдельных элементов, найдены ПФ разомкнутой и замкнутой системы.
С помощью критерия Вышнеградского определена область устойчивости системы относительно двух параметров.
Анализ устойчивости замкнутой системы с использованием различных методов подтвердил устойчивость замкнутой системы, что свидетельствует о правильности расчётов.
Литература
1. Бабаков, Н А. Теория автоматического управления: учебное пособие
для ВУЗов /Н А Бабаков, А.А. Воронов -М. : Высш. Шк., 1977.
2. Бесекерский, В А. Теория систем автоматического регулирования /
В.А. Бесекерский, Е.П. Попов. - М. : Наука, 1997
3 Келим, Ю М. Методические указания, задания на контрольную и
курсовую работы по курсу по курсу «Теория управления» / Ю.М. Келим. -
М. : Наука, 1997.
4. Пупков, К. А. Методы классической и современной теории автоматического управления. Т.1: Анализ и статистическая динамика систем автоматического управления / К.А. Пупков, А.И. Баркин, Е.И. Воронов,
Н.Д. Егупов и др. - М. . Изд-во МГТУ им. Н.Э.Баумана, 2000.


Изм.
Кол.уч
№ док.
Подпись
Дата
Лист
- -
Лист

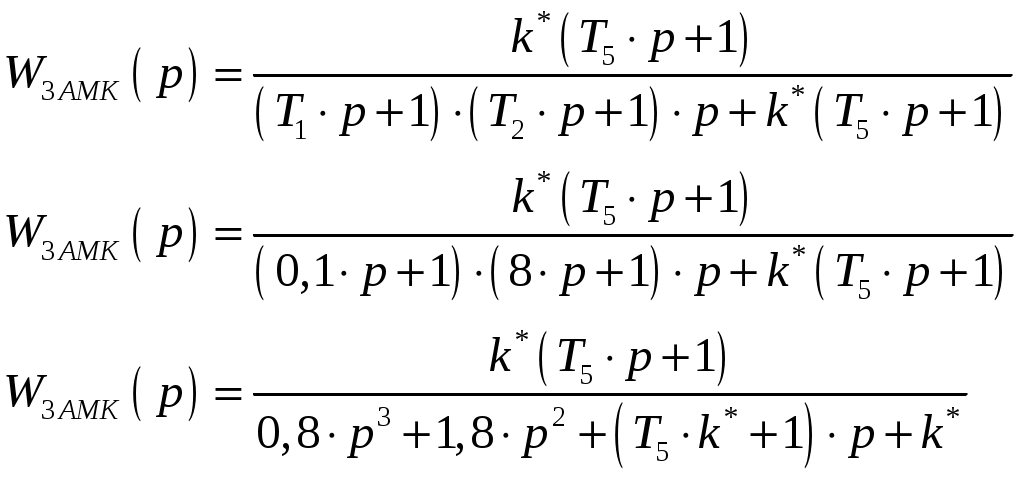
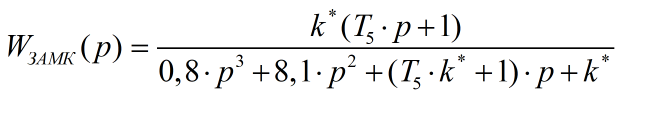
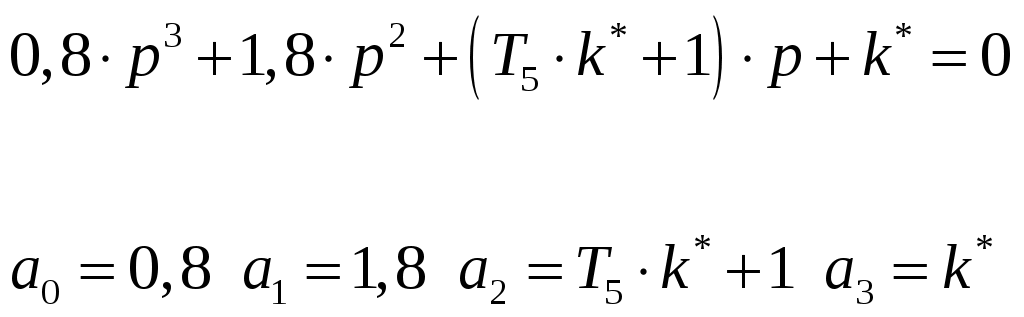
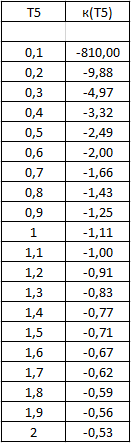
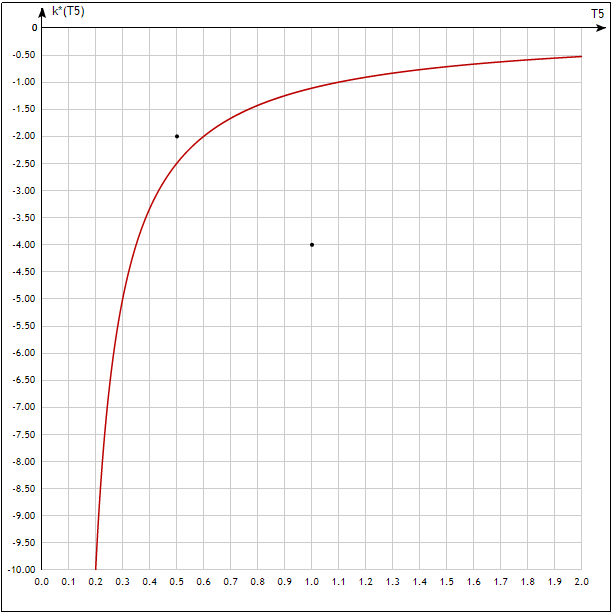
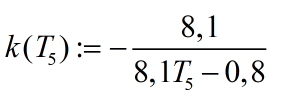 Из этого уравнения вычисляем k* при заданных значениях Т5.
Из этого уравнения вычисляем k* при заданных значениях Т5.