Главная страница
Навигация по странице:

  • 2. Установите соответствие между типом корней и характером переходного процесса

  • Переходный процесс Тип корней

  • 3. Дайте характеристику способам оценки устойчивости

  • 4. Укажите, какие из нижеперечисленных признаков относятся к критерию устойчивости Гурвица

  • 5. Чем отличаются необходимые и достаточные условия устойчивости

  • 6. Укажите, какие из нижеперечисленных признаков относятся к критерию устойчивости Найквиста

  • 7. Система имеет характеристическое уравнение

  • 8. Определите диапазон значений K , при которых система устойчива

  • 9. Можно ли сделать вывод об устойчивости системы по характеристическому уравнению без вычислений Почему

  • 10. Годограф на каком рисунке соответствует устойчивой системе Можно ли определить ее порядок

    		•

    ТАУ-Устойчивость. Задание по устойчивости. Зиганшина Задание по разделу Устойчивость Установите соответствие между входным сигналом и реакцией системы


    Скачать 0.62 Mb.
    НазваниеЗиганшина Задание по разделу Устойчивость Установите соответствие между входным сигналом и реакцией системы
    АнкорТАУ-Устойчивость
    Дата26.05.2020
    Размер0.62 Mb.
    Формат файлаdocx
    Имя файлаЗадание по устойчивости.docx
    ТипДокументы
    #125748

    Зиганшина

    Задание по разделу «Устойчивость»
    1. Установите соответствие между входным сигналом и реакцией системы


    Входное воздействие
    Реакция системы

    а) единичное ступенчатое воздействие
    1) Весовая функция

    б) дельта-функция
    2) Гармоническая функция

    в) гармоническое воздействие
    3) Переходная характеристика


    Ответ (в виде трехзначной цифры): 312.
    2. Установите соответствие между типом корней и характером переходного процесса


    Переходный процесс



    Тип корней


    А) Затухающий



    1) все корни характеристического уравнения вещественные (зависит от знака)


    Б) Расходящийся



    2) хотя бы один из корней имеет положительную вещественную часть


    В) Нейтральный



    3) все корни характеристического уравнения комплексно-сопряженные (зависит от вещ. части)







    4) хотя бы один из корней имеет нулевую вещественную часть

    5) вещественные части всех корней характеристического уравнения отрицательны










    Ответ :

    А 5

    Б 2

    В 4
    3. Дайте характеристику способам оценки устойчивости


    Способ/ метод оценки
    Достоинства
    Недостатки
    Для каких систем/ когда применяется

    Критерий Гурвица
    Удобен для реализации на ЭВМ
    Практическое вычисление определителей становится трудоемким при порядке систем n>4; малая наглядность
    Известно характеристическое уравнение системы

    Критерий Найквиста
    Исследование разомкнутой САУ проще, чем замкнутой; наглядность; отсутствие ограничений на порядок дифференциального уравнения

    -
    Известна АФЧХ разомкнутой системы


    Продолжение таблицы 1

    Критерий Михайлова
    Наглядность, отсутствие ограничений на порядок дифференциального уравнения

    Определение влияния параметров системы на ее устойчивость практически невозможно
    Известно уравнение замкнутой системы


    4. Укажите, какие из нижеперечисленных признаков относятся к критерию устойчивости Гурвица
    Признаки:

    1) АФЧХ разомкнутой системы не охватывает точку (–1; j0)

    2) правая часть характеристического уравнения равна нулю

    3) все определители неотрицательны

    4) АФЧХ замкнутой системы не охватывает точку (–1; j0)

    5) все коэффициенты характеристического уравнения положительны

    6) коэффициент при старшей степени равен единице

    7) все определители положительны
    Ответ (в виде числа): 2357
    5. Чем отличаются необходимые и достаточные условия устойчивости?


    При выполнении необходимого условия устойчивости, система может быть устойчива.

    Проверка необходимого условия нужна для «отсеивания» дальнейшего исследования систем.


    6. Укажите, какие из нижеперечисленных признаков относятся к критерию устойчивости Найквиста?
    Признаки

    1) АФЧХ замкнутой системы не охватывает точку (–1; j0)

    2) АФЧХ начинается на положительной части вещественной оси

    3) все определители неотрицательны

    4) правая часть характеристического уравнения равна нулю

    5) АФЧХ разомкнутой системы не охватывает точку (–1; j0)

    6) все определители положительны

    7) все коэффициенты характеристического уравнения положительны
    Ответ (в виде числа): 1257
    7. Система имеет характеристическое уравнение:
    s3+20s2+5s+100=0
    Определите, устойчива ли система.
    Ответ: Выполняется необходимое условие устойчивости – положительны все коэффициенты характеристического уравнения.

    Следовательно, вычисляем критерий Гурвица для системы третьего порядка: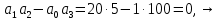

    система находится на границе устойчивости
    8. Определите диапазон значений K, при которых система устойчива
    s3+20s2+5s+K=0.
    Ответ: Для выполнения необходимого условия устойчивости .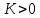

    По критерию Гурвица система устойчива, если: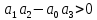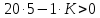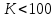







    Ответ: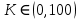
    9. Можно ли сделать вывод об устойчивости системы по характеристическому уравнению без вычислений? Почему?
    s3–4s2+6s+100=0
    Ответ: Неустойчива, т.к. не выполняется необходимое условие устойчивости – положительны не все коэффициенты характеристического уравнения.
    10. Годограф на каком рисунке соответствует устойчивой системе? Можно ли определить ее порядок?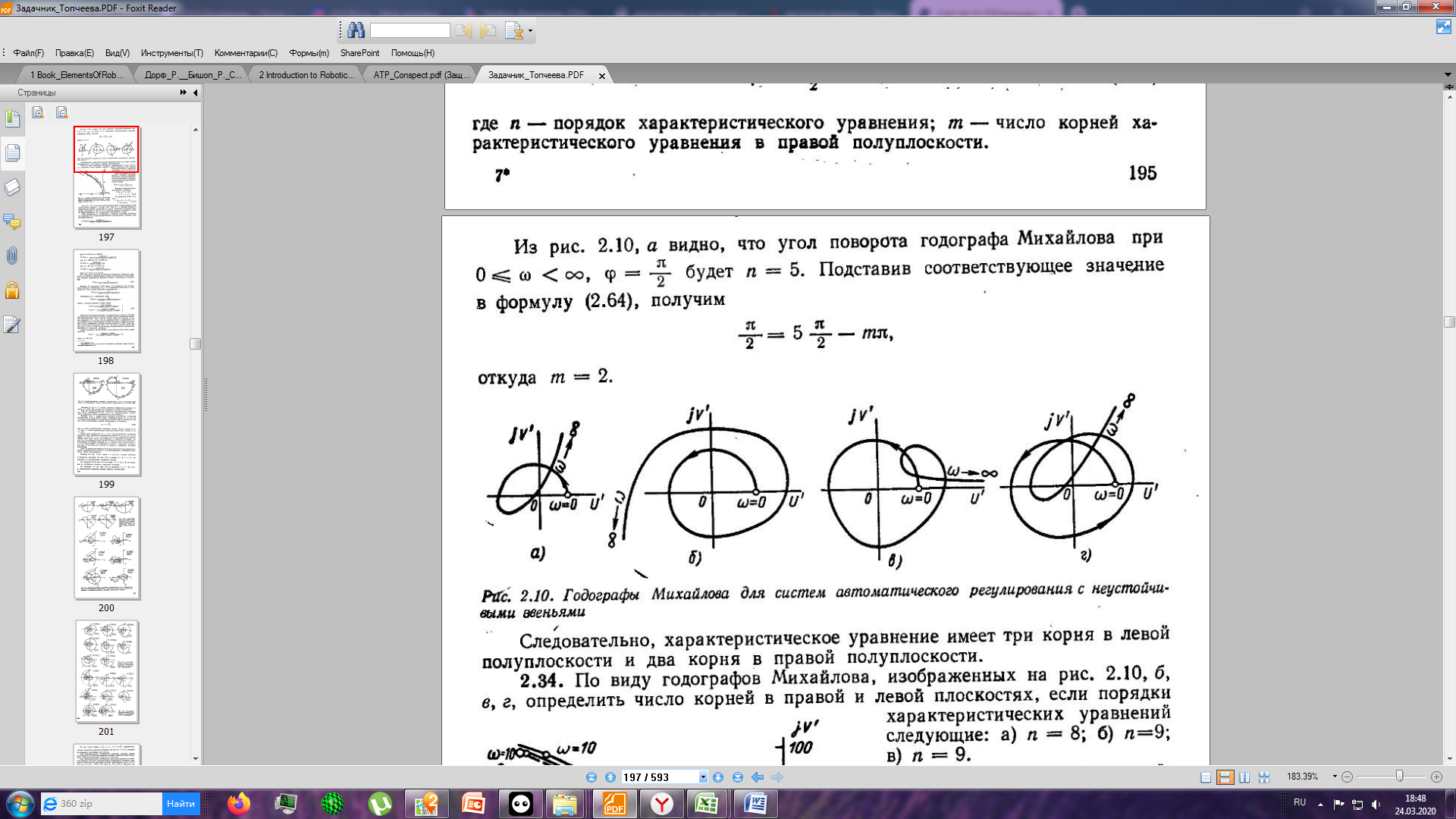

    Ответ: По критерию Михайлова устойчивая система приведена на рисунке Б, где кривая начинается на вещественной положительной полуоси с ростом частота от 0 до обходит последовательно в положительном направлении n квадрантов комплексной плоскости (n – степень характеристического уравнения – 7).

    написать администратору сайта