1.4. Применение закона Био–Савара–Лапласа.
Магнитное поле кругового тока
Рассмотрим проводник в форме окружности радиуса R, по которому протекает ток I (рис. 11). Разобьем круговой ток на элементы тока 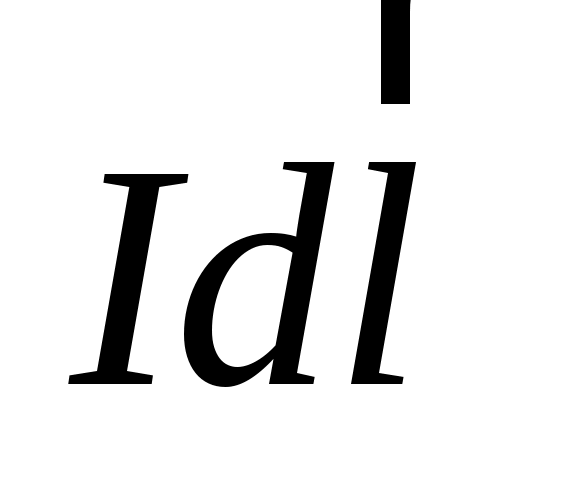 , каждый из которых создает в центре кругового тока (точка О) магнитное поле , каждый из которых создает в центре кругового тока (точка О) магнитное поле 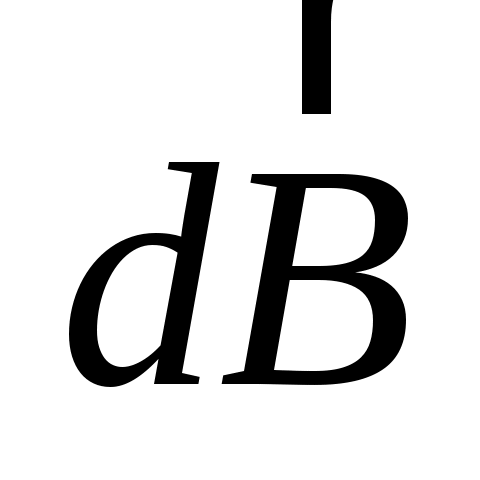 . По закону Био–Савара–Лапласа (1.1), с учетом, что . По закону Био–Савара–Лапласа (1.1), с учетом, что 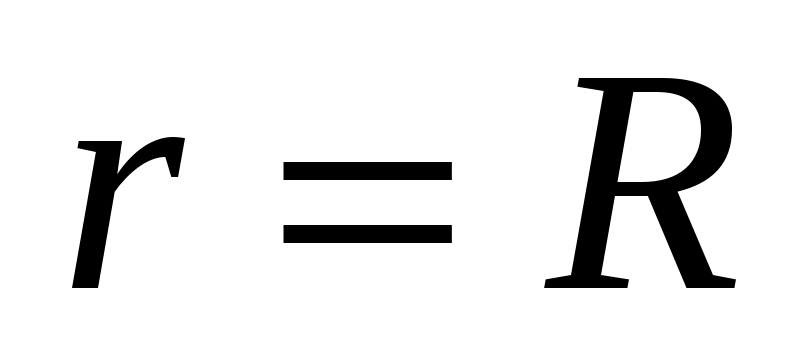 , магнитная индукция, создаваемая элементом тока в точке О, определяется формулой , магнитная индукция, создаваемая элементом тока в точке О, определяется формулой
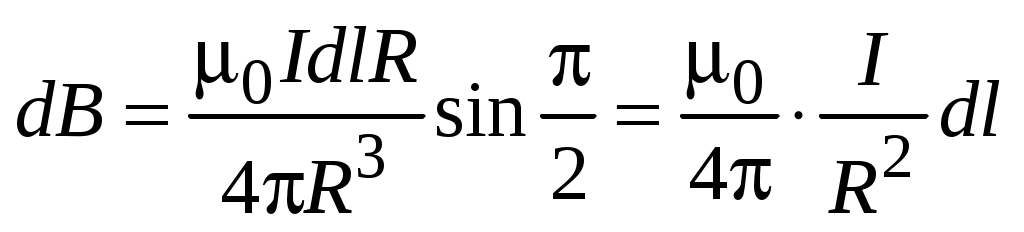 . .
П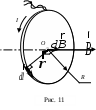 о принципу суперпозиции о принципу суперпозиции 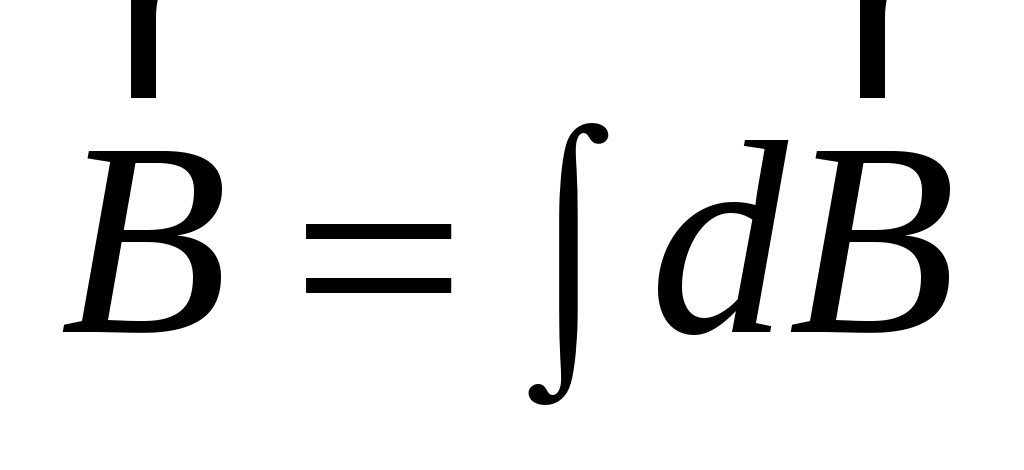 . В точке О все . В точке О все 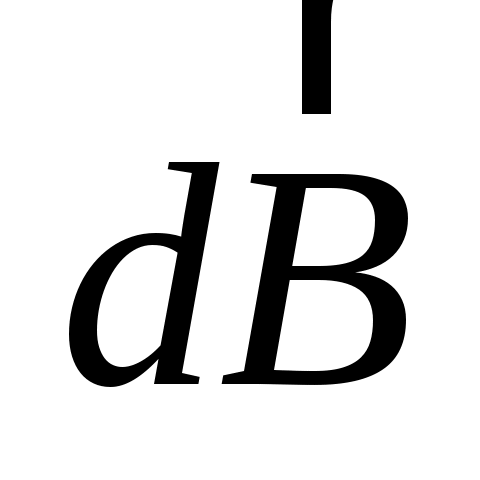 от разных элементов кругового тока имеют одинаковое направление. Следовательно, от разных элементов кругового тока имеют одинаковое направление. Следовательно,
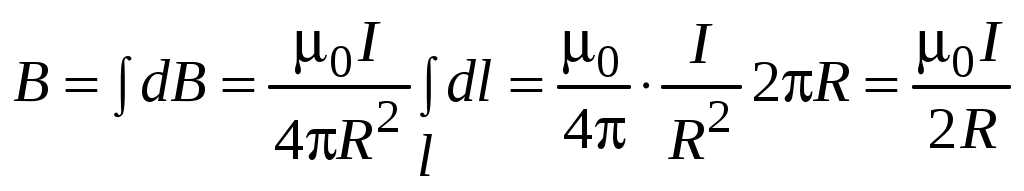 . .
Таким образом, для индукции магнитного поля в центре кругового тока получаем
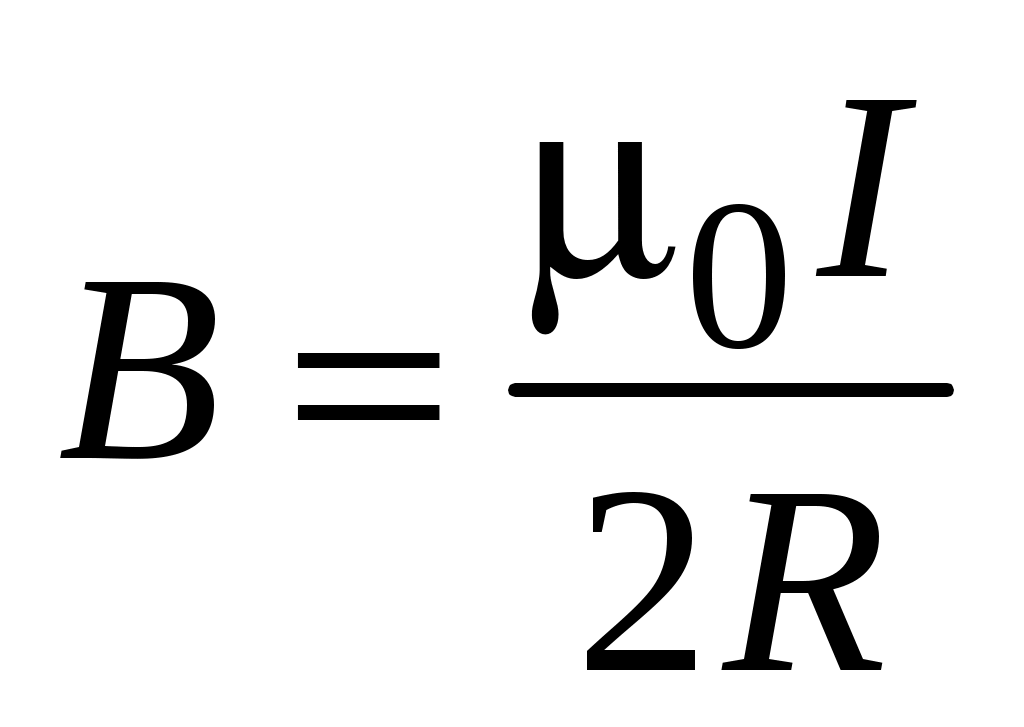 . (1.7) . (1.7)
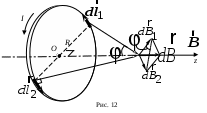
Рассмотрим магнитное поле, создаваемое круговым током в других точках на оси z (рис. 12).
Л
z
юбая пара равных по величине элементов тока (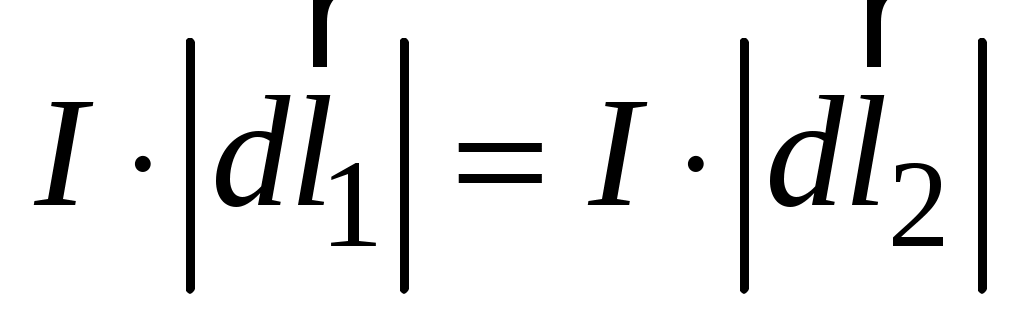 ), расположенная симметрично относительно оси z, создает в точках на оси магнитное поле: ), расположенная симметрично относительно оси z, создает в точках на оси магнитное поле: 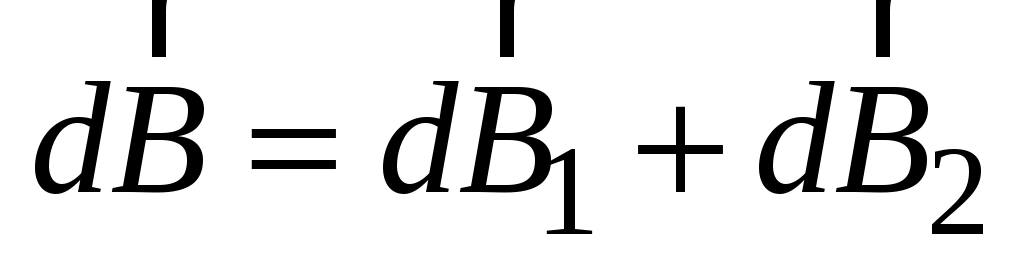 ( (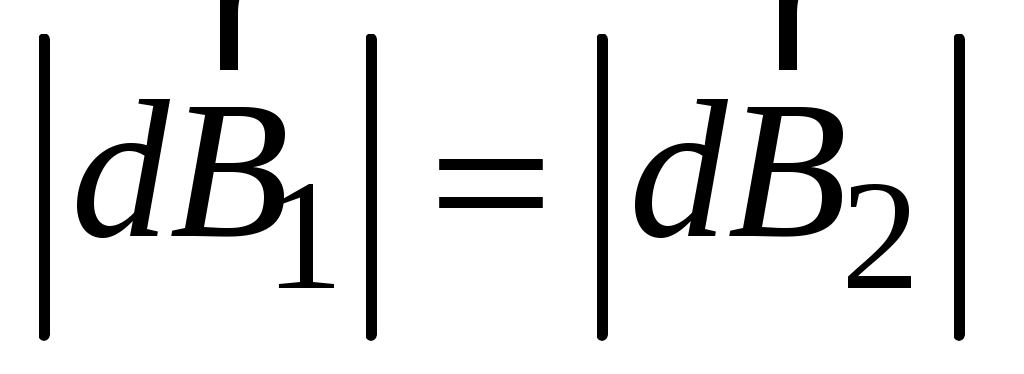 ). Вектор ). Вектор 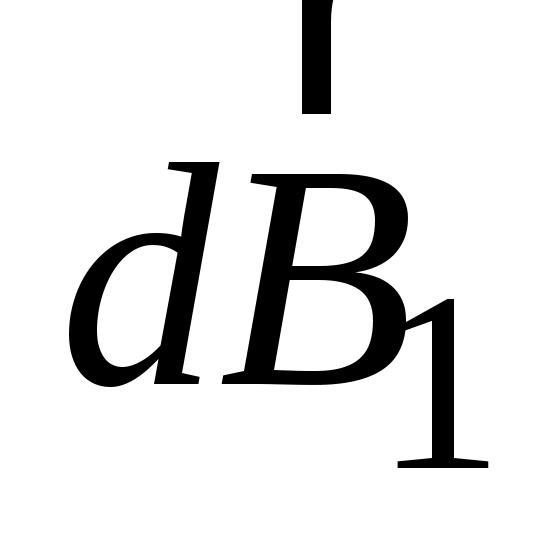 в соответствии с законом Био–Савара–Лапласа направлен перпендикулярно плоскости, содержащей вектора в соответствии с законом Био–Савара–Лапласа направлен перпендикулярно плоскости, содержащей вектора 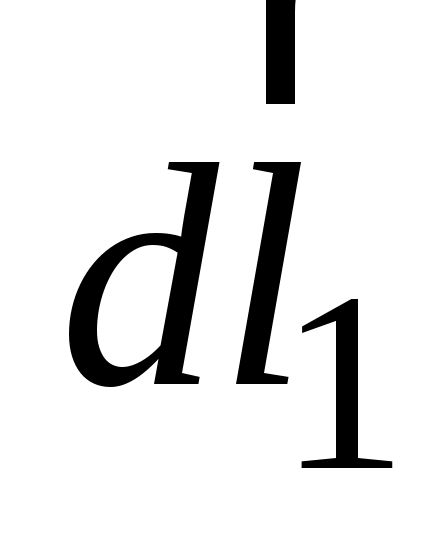 и и 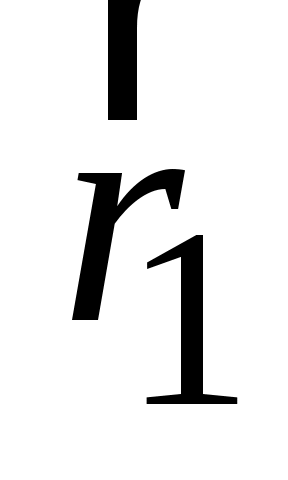 . Вектор . Вектор 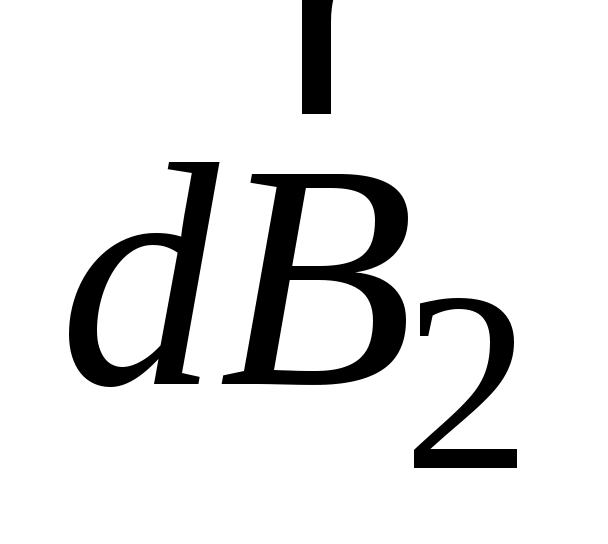 направлен перпендикулярно плоскости, содержащей вектора направлен перпендикулярно плоскости, содержащей вектора 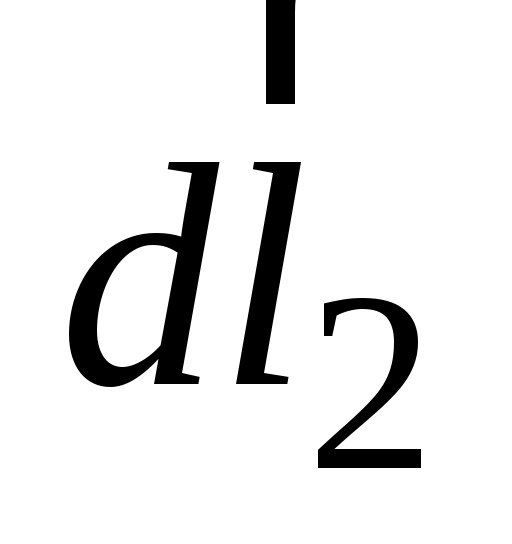 и и 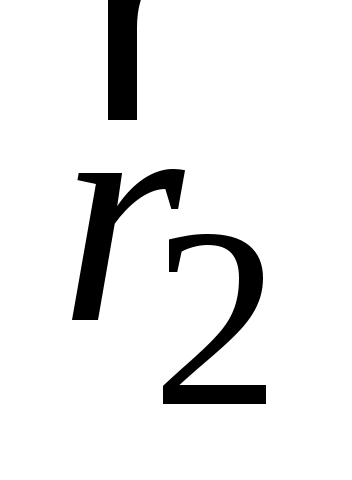 . Вектора . Вектора 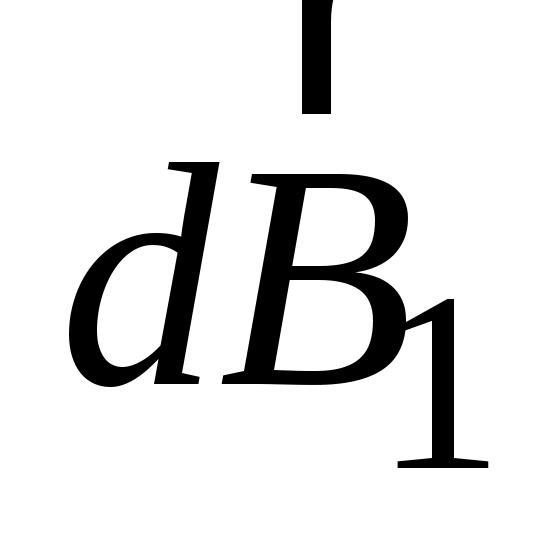 и и 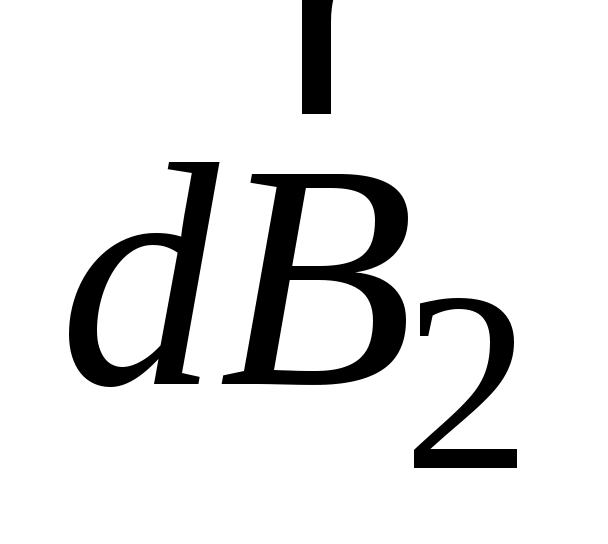 образуют ромб, диагональ которого представляет вектор образуют ромб, диагональ которого представляет вектор 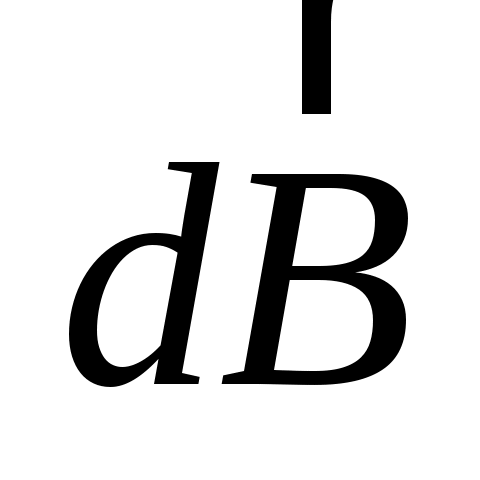 , направленный вдоль оси Оz. , направленный вдоль оси Оz.
Как следует из рис. 12,
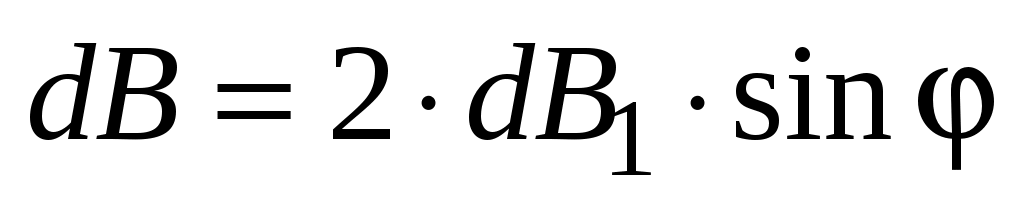 . .
Учитывая, что 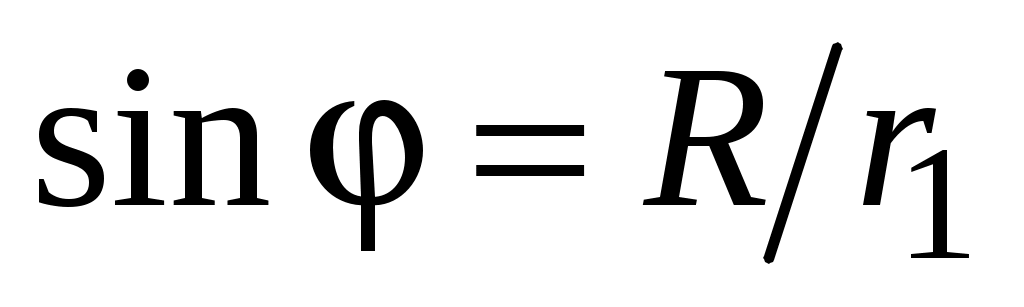 , по закону Био–Савара–Лапласа , по закону Био–Савара–Лапласа
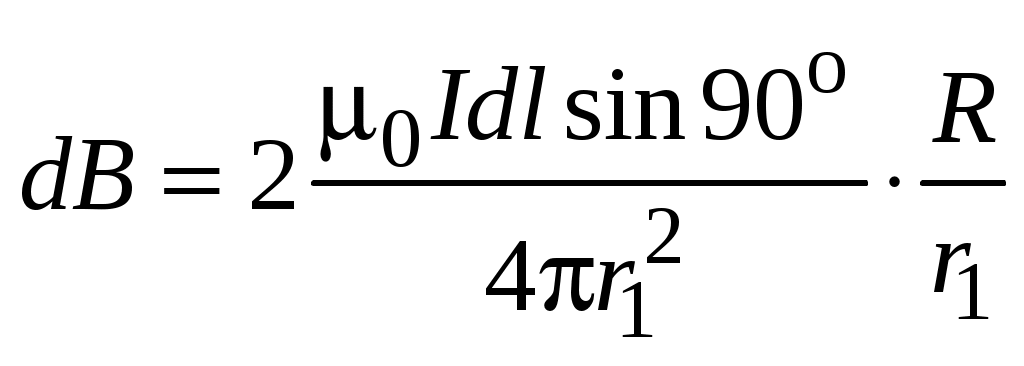 . .
Так как 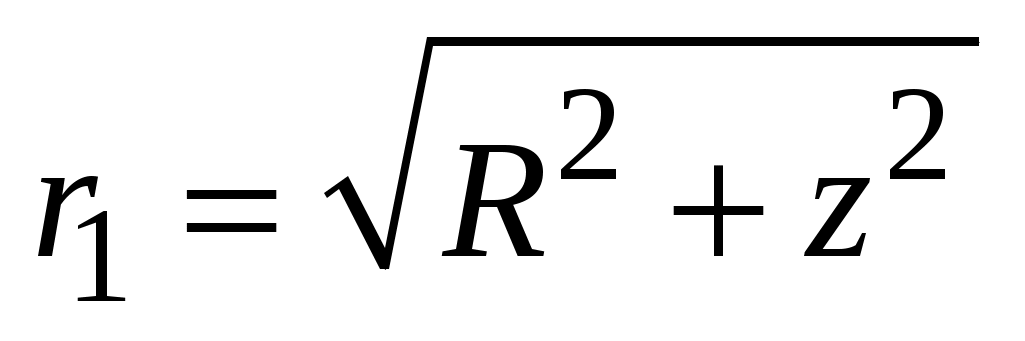 , , 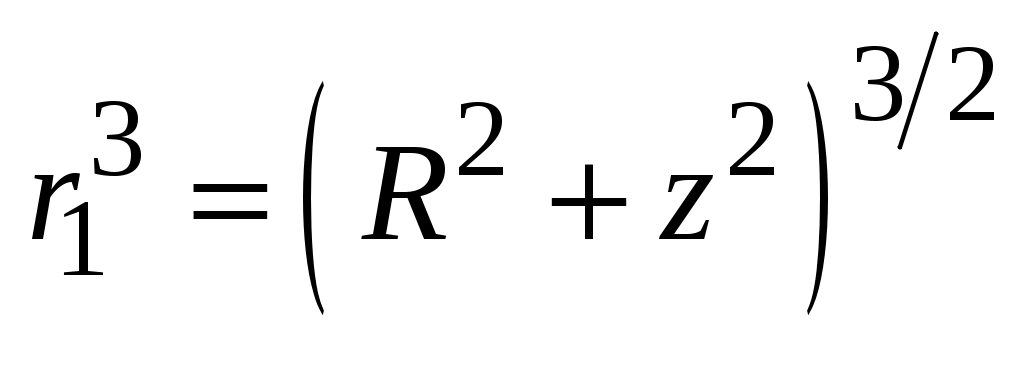 , получаем , получаем
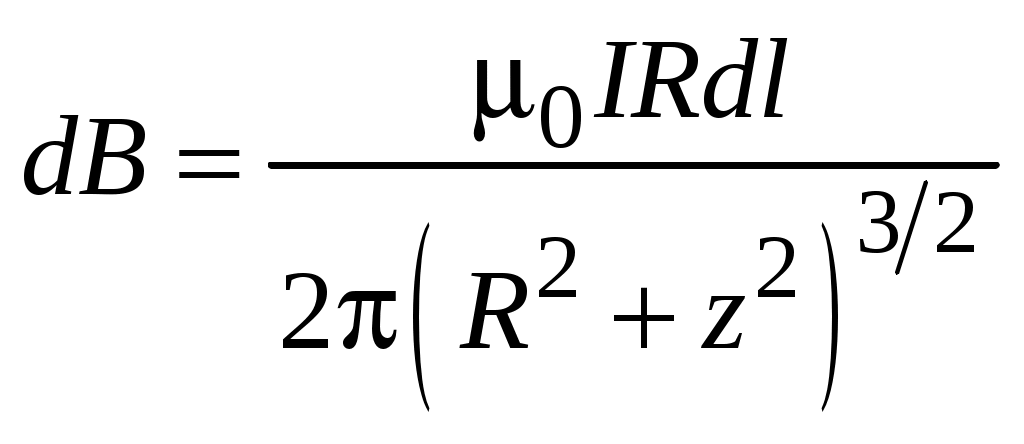 . .
По принципу суперпозиции результирующий вектор 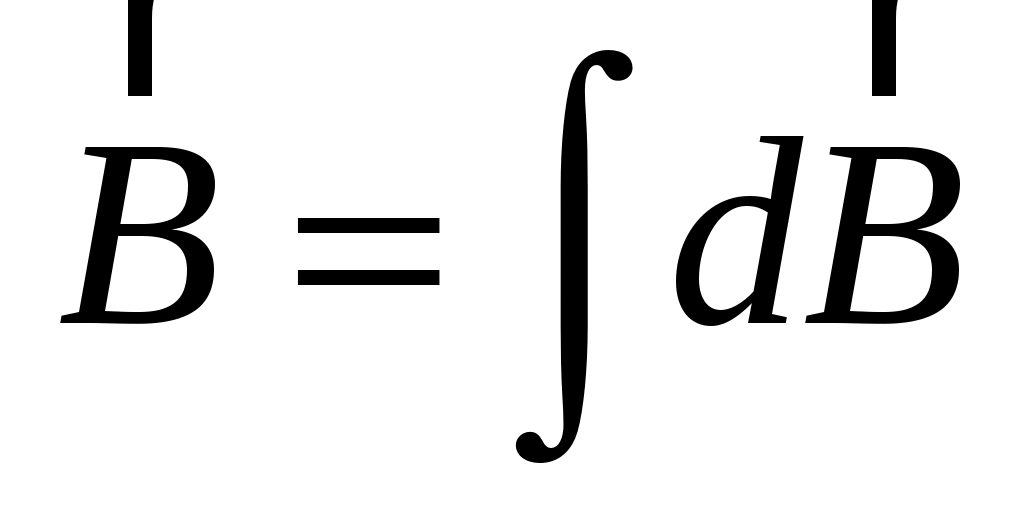 также направлен вдоль оси z, поэтому также направлен вдоль оси z, поэтому
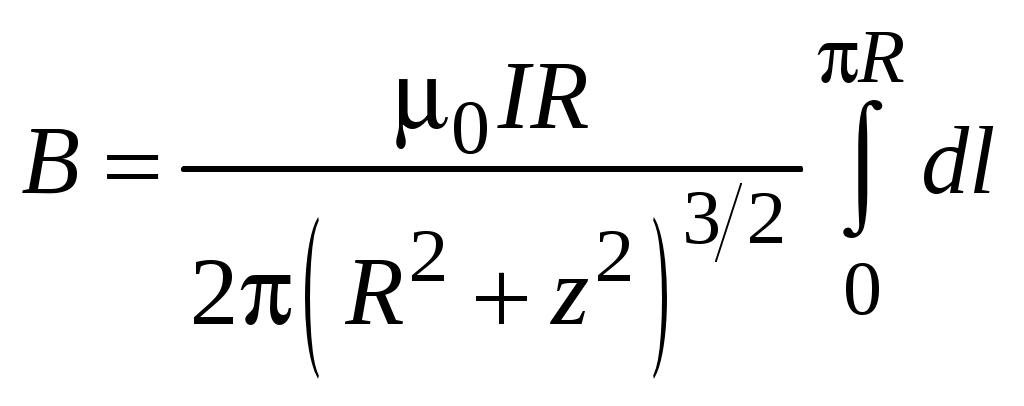 . .
Окончательное выражение для индукции в точках на оси кругового тока имеет вид
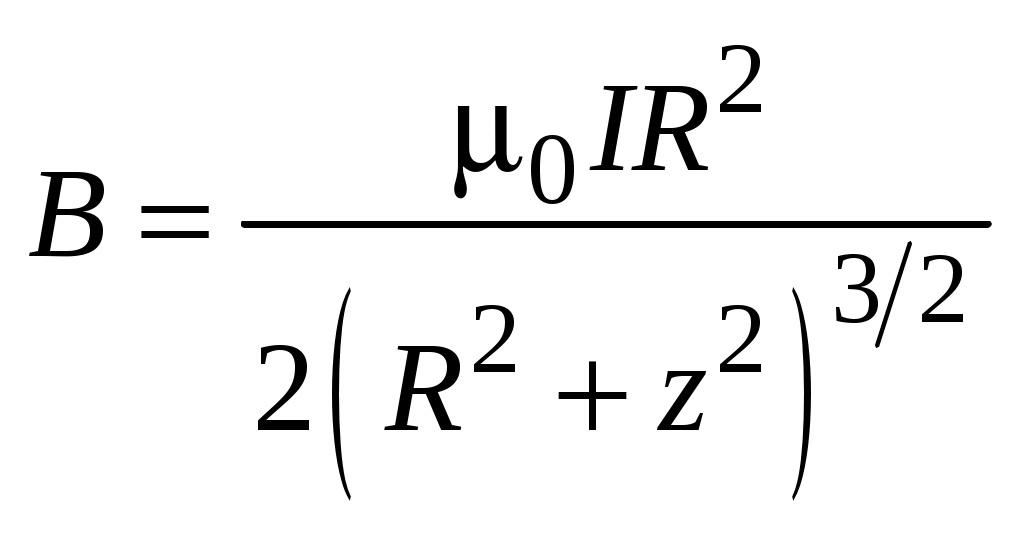 . .
|
 Скачать 2.73 Mb.
Скачать 2.73 Mb.