1.6. Теорема о циркуляции вектора магнитной индукции
(закон полного тока)
Теорема о циркуляции вектора магнитной индукции в вакууме: циркуляция вектора магнитной индукции 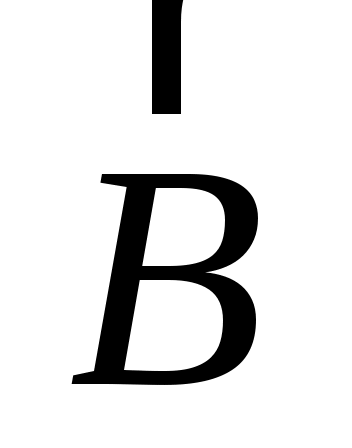 по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на 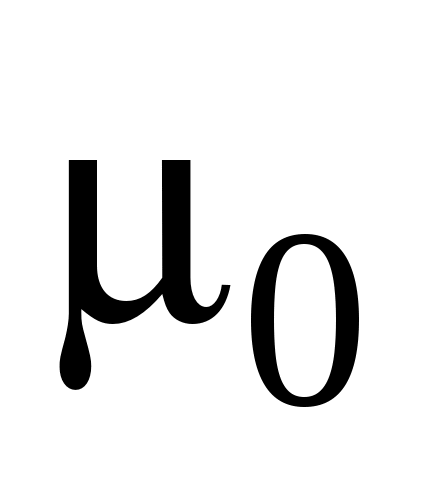 . Иначе говоря, . Иначе говоря,
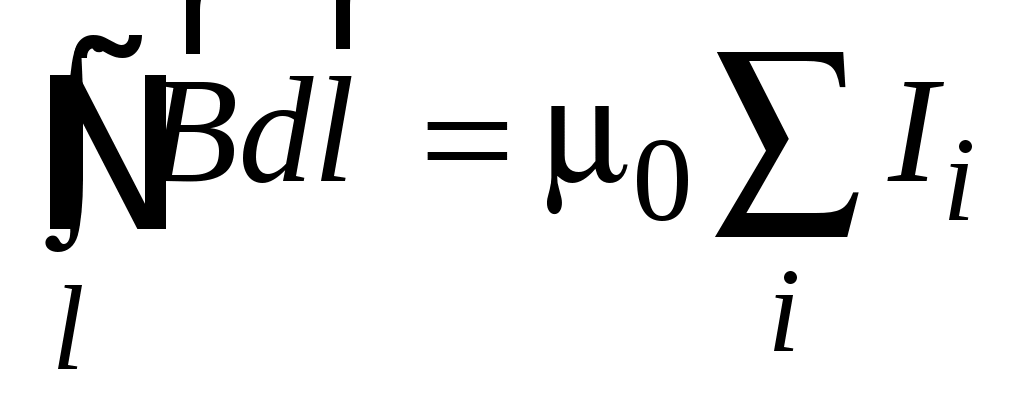 , ,
г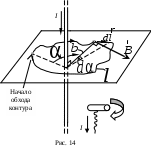 де де 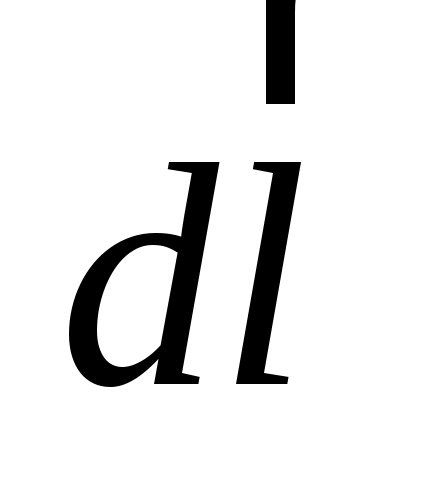 – элементарное перемещение вдоль замкнутого контура l. – элементарное перемещение вдоль замкнутого контура l.
Докажем теорему для случая, когда ток I течет по прямому бесконечно длинному проводнику, а замкнутый контур l расположен в плоскости, перпендикулярной току (рис. 14).
Циркуляция вектора магнитной индукции 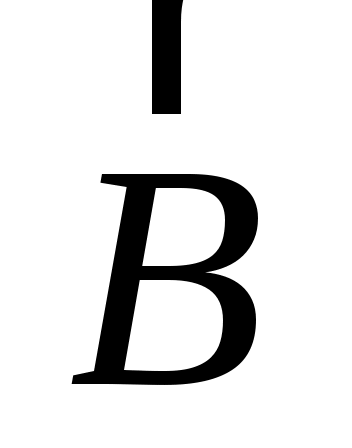 может быть записана в виде может быть записана в виде
 , ,
где 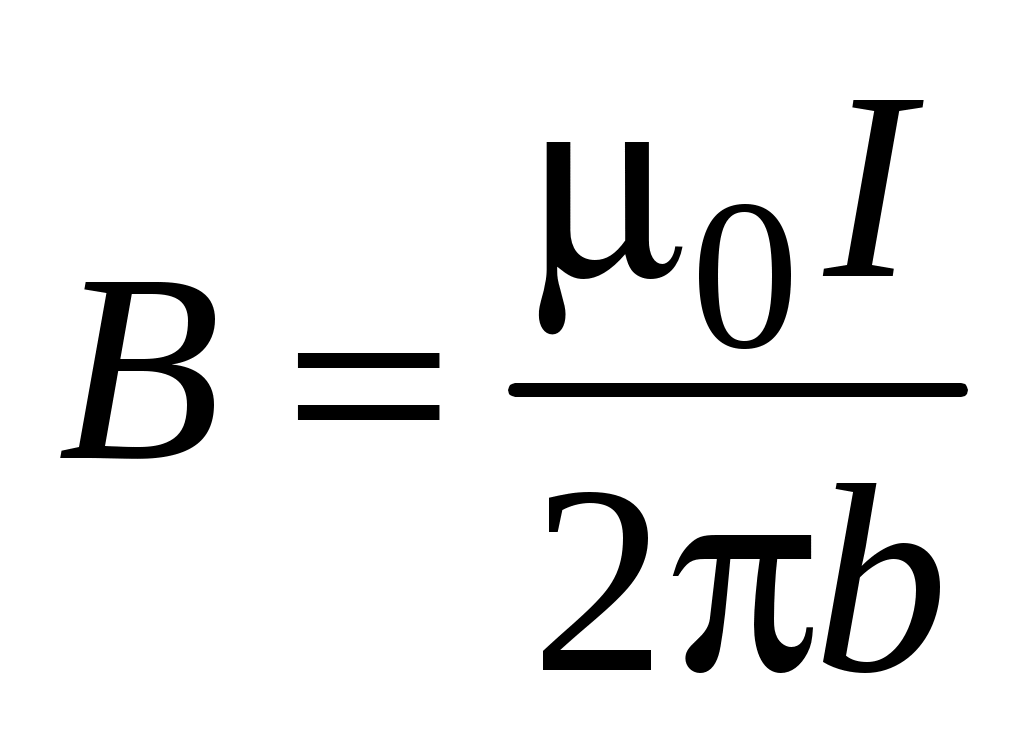 – индукция магнитного поля прямого тока; – индукция магнитного поля прямого тока;  – проекция вектора элементарного перемещения – проекция вектора элементарного перемещения 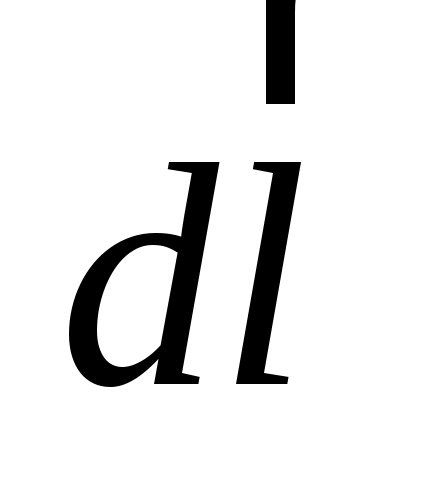 на направление вектора на направление вектора 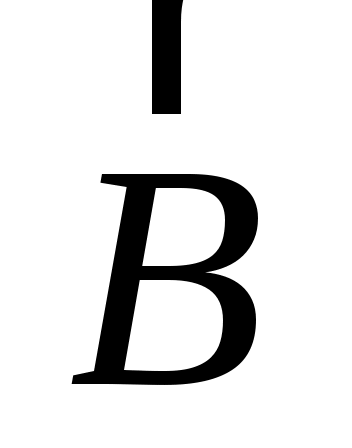 . .
И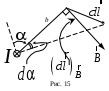 з рис. 15 видно, что з рис. 15 видно, что  с хорошей степенью точности. Таким образом, с хорошей степенью точности. Таким образом,
 (1.10) (1.10)
Если изменить направление тока на рис. 14 на противоположное, то изменится направление вектора 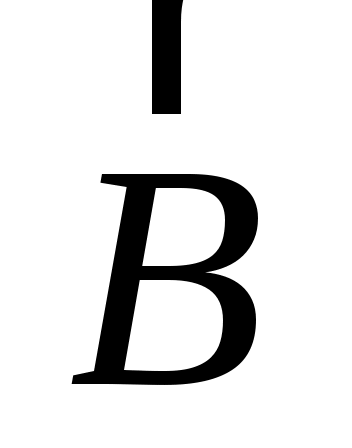 на противоположное в каждой точке пространства. Противоположной по знаку станет циркуляция вектора на противоположное в каждой точке пространства. Противоположной по знаку станет циркуляция вектора 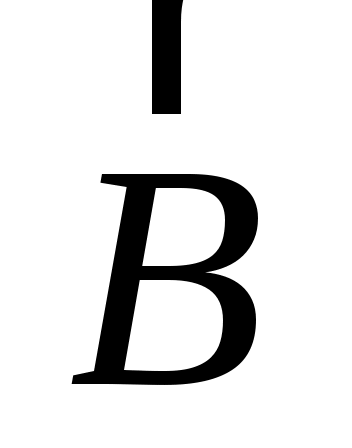 для выбранного направления обхода контура. При этом в равенстве (1.10) ток следует считать отрицательным и подставлять его значение в формулу (1.10) со знаком минус. Таким образом, ток следует считать положительным, если направление обхода контура связано с направлением тока правилом правого винта. В противном случае ток надо считать отрицательным. для выбранного направления обхода контура. При этом в равенстве (1.10) ток следует считать отрицательным и подставлять его значение в формулу (1.10) со знаком минус. Таким образом, ток следует считать положительным, если направление обхода контура связано с направлением тока правилом правого винта. В противном случае ток надо считать отрицательным.
Е сли контур l не охватывает ток (рис. 16), то сли контур l не охватывает ток (рис. 16), то
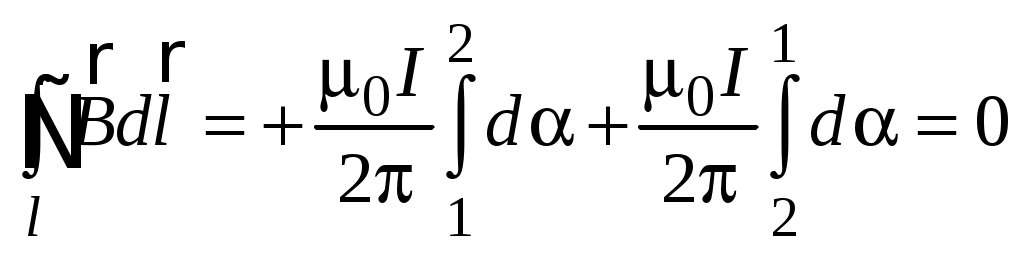 . .
В случае контура произвольной формы (рис. 17) элементарное перемещение 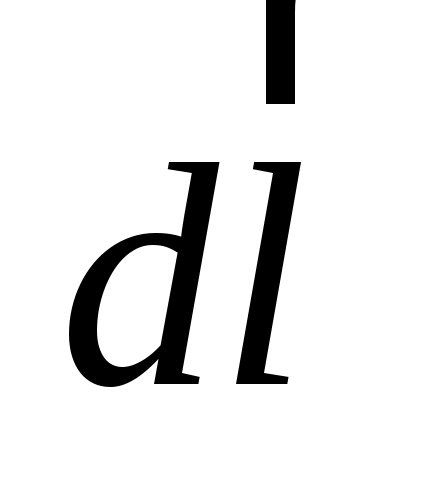 разложим на две составляющие, перпендикулярную разложим на две составляющие, перпендикулярную  и параллельную и параллельную  вектору магнитной индукции: вектору магнитной индукции:

Так как  доказательство теоремы для случая контура произвольной формы сводится к рассмотренному выше случаю. доказательство теоремы для случая контура произвольной формы сводится к рассмотренному выше случаю.
М ожно показать, что теорема о циркуляции ожно показать, что теорема о циркуляции 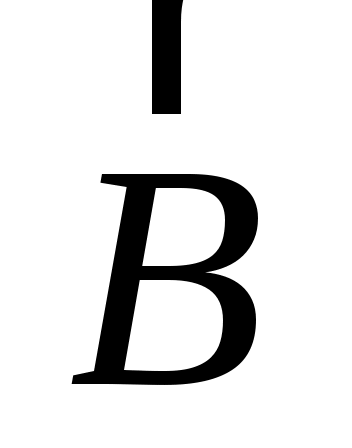 (или закон полного тока) справедлива в общем случае для системы токов произвольной формы и произвольного замкнутого контура: (или закон полного тока) справедлива в общем случае для системы токов произвольной формы и произвольного замкнутого контура:
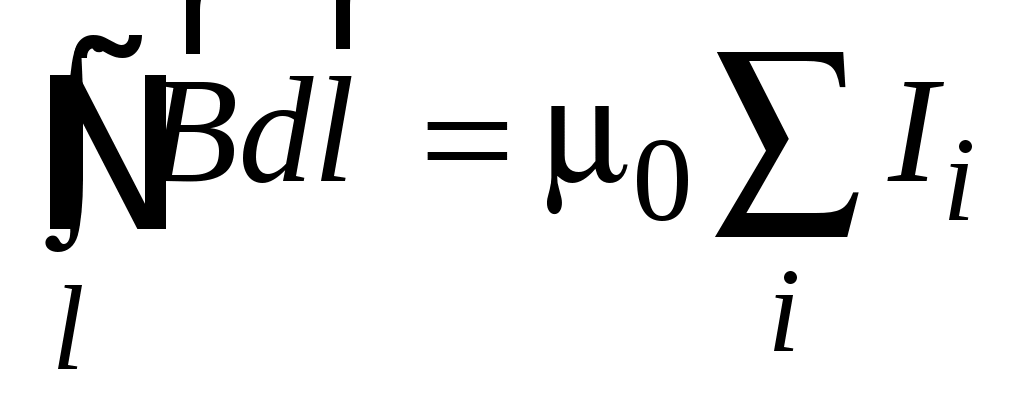 , (1.11) , (1.11)
где  – токи, охватываемые контуром, причем – токи, охватываемые контуром, причем  берется с плюсом, если направление берется с плюсом, если направление  и направление обхода контура связаны правилом правого винта, и с минусом в противном случае. и направление обхода контура связаны правилом правого винта, и с минусом в противном случае.
Если контур находится в проводящей среде, в которой существует упорядоченное движение зарядов, теорему (1.11) удобно представить в виде
 , ,
где S – любая поверхность, ограниченная контуром l;  – проекция плотности тока на нормаль к элементу поверхности – проекция плотности тока на нормаль к элементу поверхности  . .
|
 Скачать 2.73 Mb.
Скачать 2.73 Mb.