Как было отмечено в подразд. 1.2, элемент тока 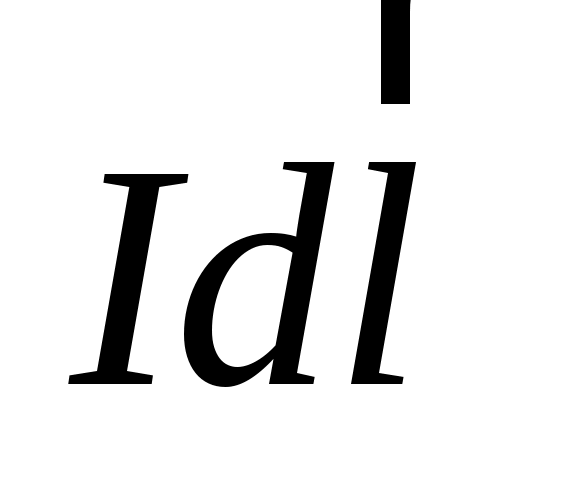 создает магнитное поле. Но такой элемент тока представляет собой совокупность упорядоченно движущихся заряженных частиц. Логично предположить, что в основе появления магнитного поля лежит движение отдельно взятой заряженной частицы, а упорядоченное движение множества таких частиц (носителей тока) приводит к пропорциональному увеличению значения магнитной индукции. Такое предположение подтверждается тем, что пучки движущихся заряженных частиц, например электронов в электронно-лучевой трубке, создают магнитное поле [4]. создает магнитное поле. Но такой элемент тока представляет собой совокупность упорядоченно движущихся заряженных частиц. Логично предположить, что в основе появления магнитного поля лежит движение отдельно взятой заряженной частицы, а упорядоченное движение множества таких частиц (носителей тока) приводит к пропорциональному увеличению значения магнитной индукции. Такое предположение подтверждается тем, что пучки движущихся заряженных частиц, например электронов в электронно-лучевой трубке, создают магнитное поле [4].
Вычислим значение индукции магнитного поля 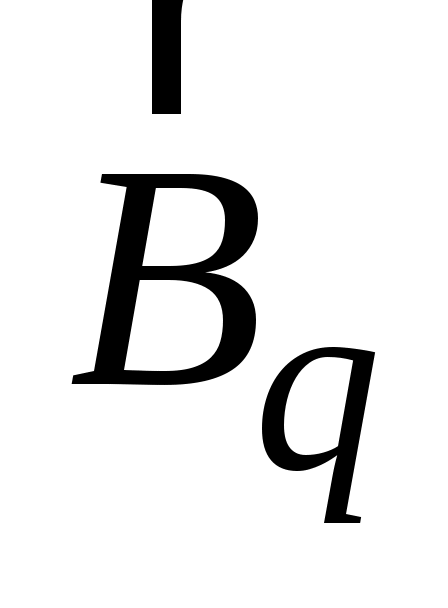 , создаваемого отдельной движущейся заряженной частицей, исходя из закона Био–Савара–Лапласа: , создаваемого отдельной движущейся заряженной частицей, исходя из закона Био–Савара–Лапласа:
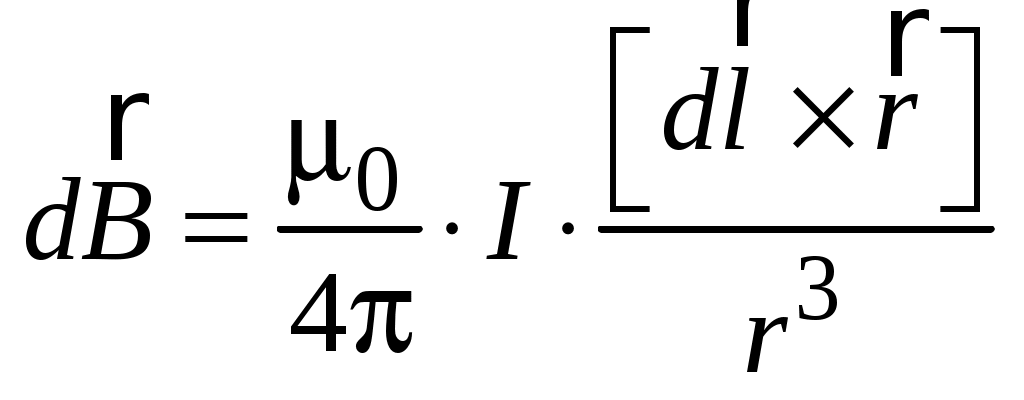 . .
Для простоты предположим, что все носители тока в элементе тока 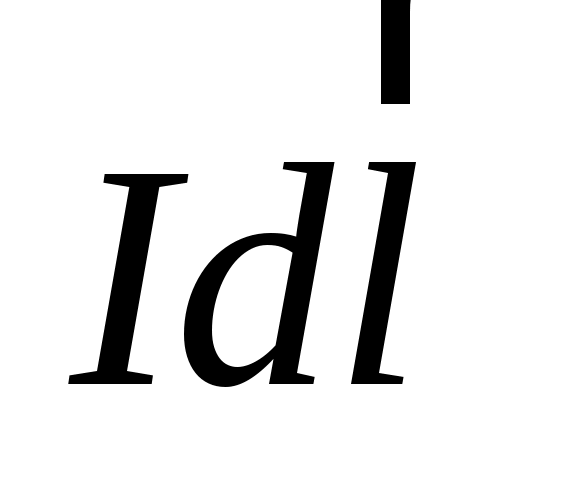 имеют одинаковый заряд имеют одинаковый заряд 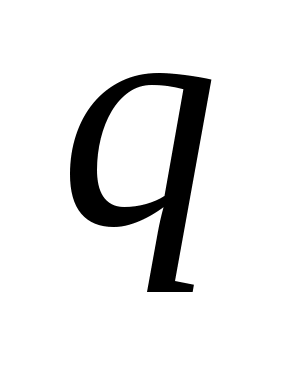 и одинаковую скорость упорядоченного движения и одинаковую скорость упорядоченного движения  . Пусть концентрация заряженных частиц, т. е. их число в единице объема, равна n, а площадь поперечного сечения элемента тока равна S. Тогда, в предположении равномерного распределения тока по сечению проводника, сила тока . Пусть концентрация заряженных частиц, т. е. их число в единице объема, равна n, а площадь поперечного сечения элемента тока равна S. Тогда, в предположении равномерного распределения тока по сечению проводника, сила тока 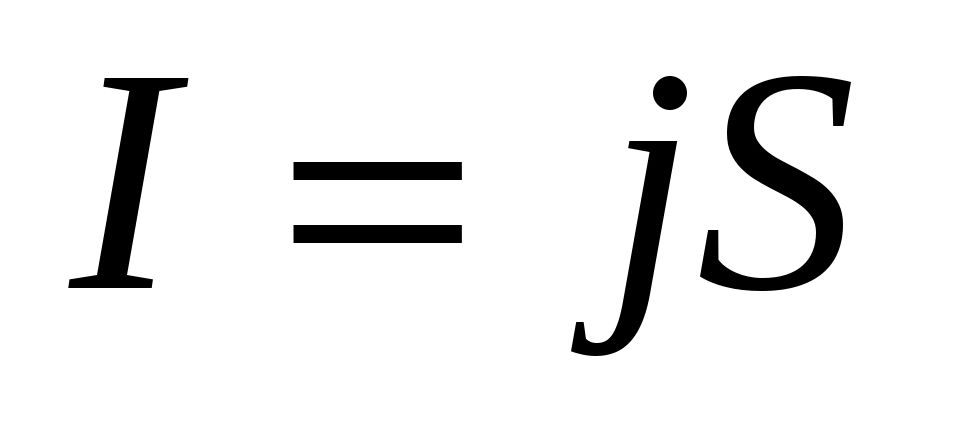 . Плотность тока . Плотность тока 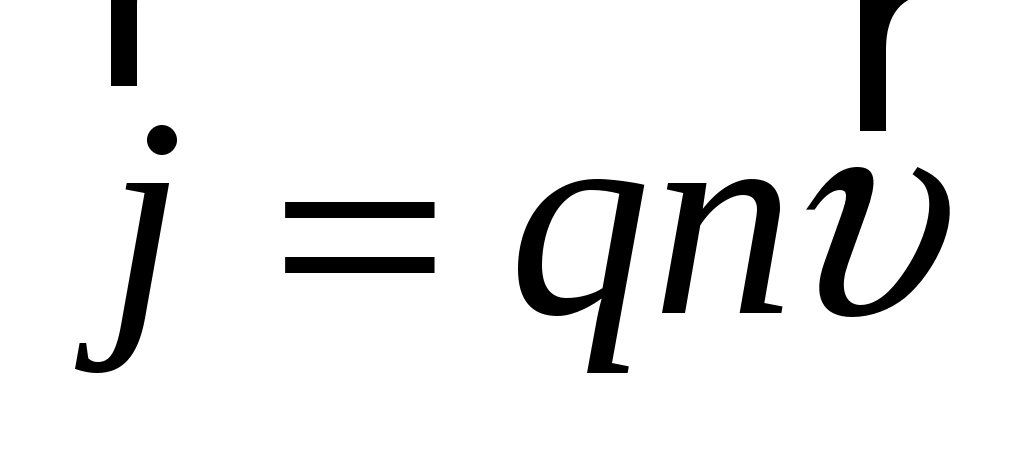 [5]. Выражение для элемента тока можно преобразовать следующим образом: [5]. Выражение для элемента тока можно преобразовать следующим образом:
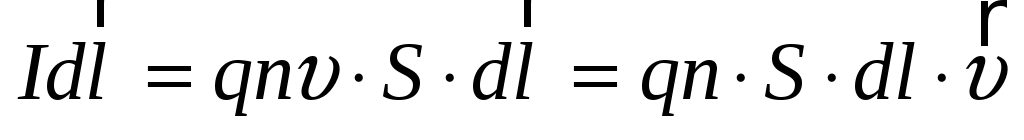 , ,
где учтено, что векторы 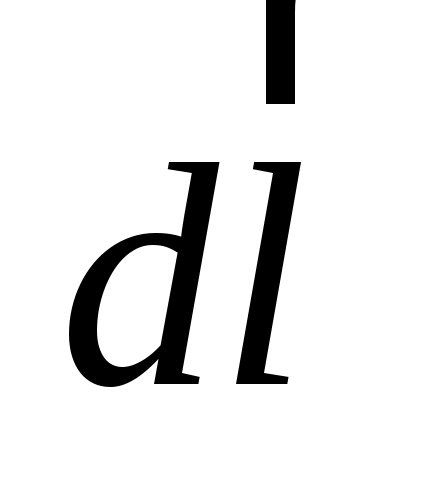 и и 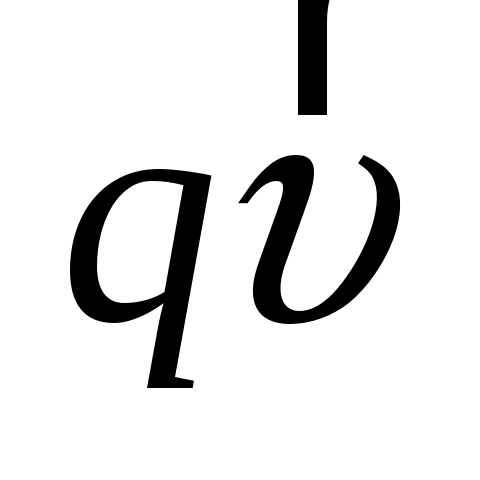 имеют одинаковое направление. Так как имеют одинаковое направление. Так как 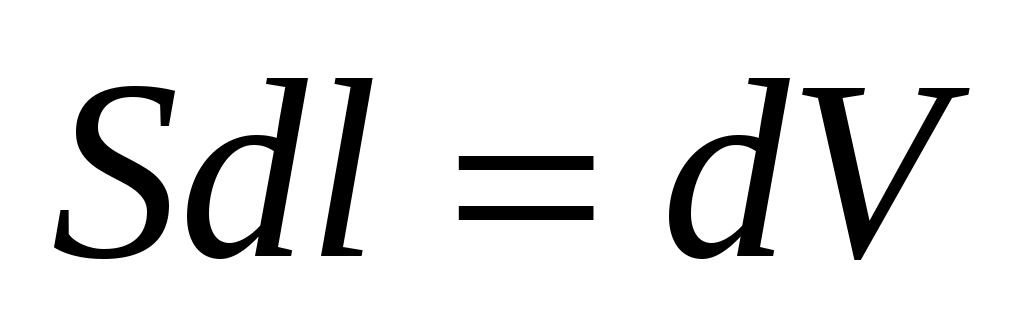 – объем элемента тока, то – объем элемента тока, то 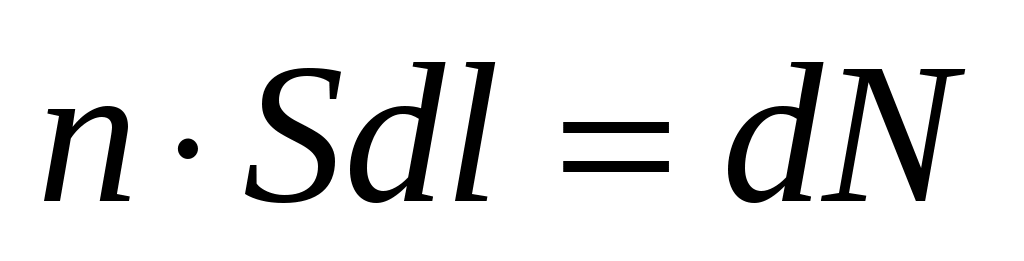 – число носителей тока в этом элементе. Тогда – число носителей тока в этом элементе. Тогда 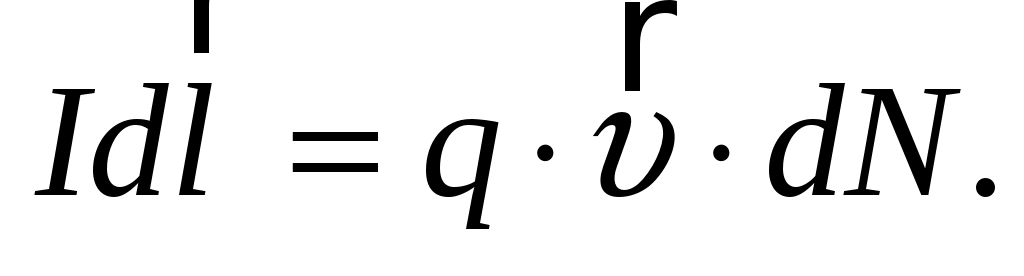 Умножим обе части равенства векторно на Умножим обе части равенства векторно на 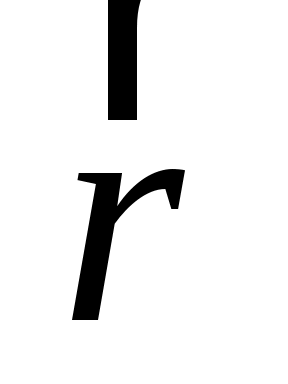 : : 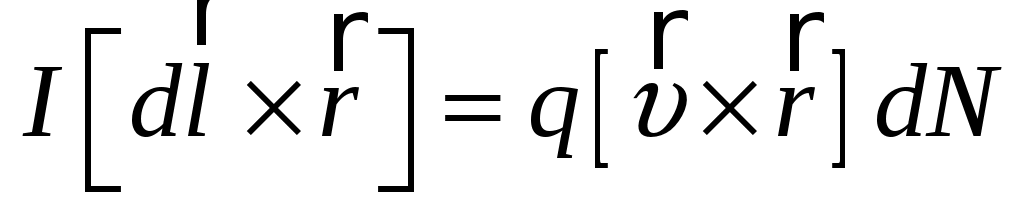 – и подставим в (1.1). В результате получим – и подставим в (1.1). В результате получим
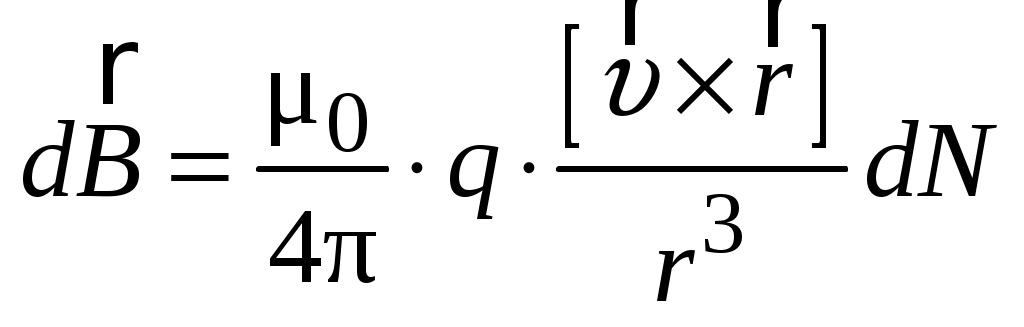 . .
Последнее равенство перепишем в виде
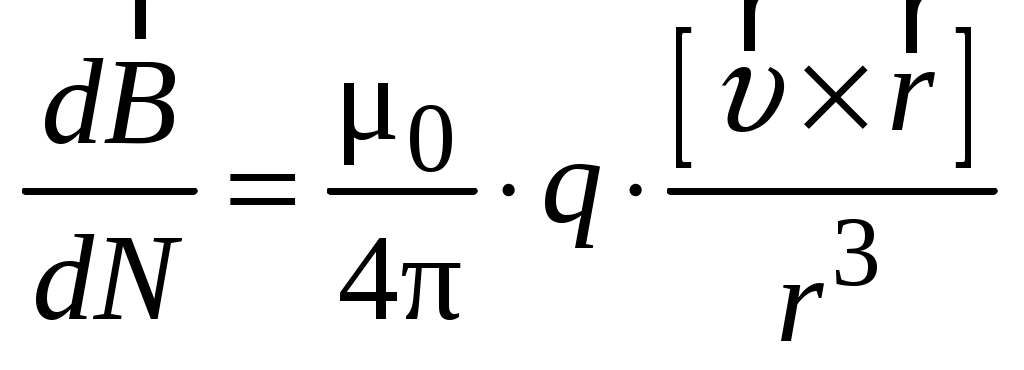 , ,
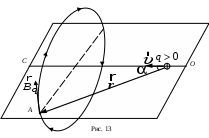
где 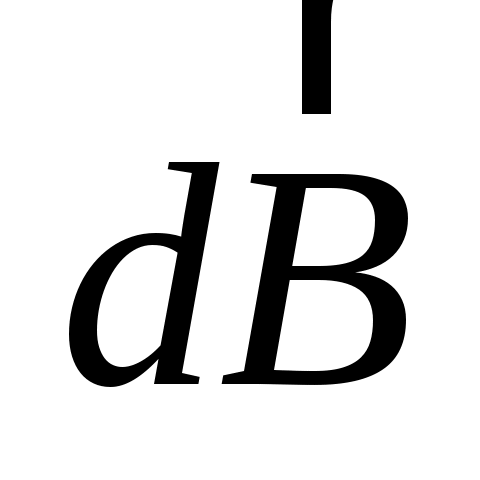 – индукция магнитного поля, создаваемого совокупностью движущихся заряженных частиц ( – индукция магнитного поля, создаваемого совокупностью движущихся заряженных частиц (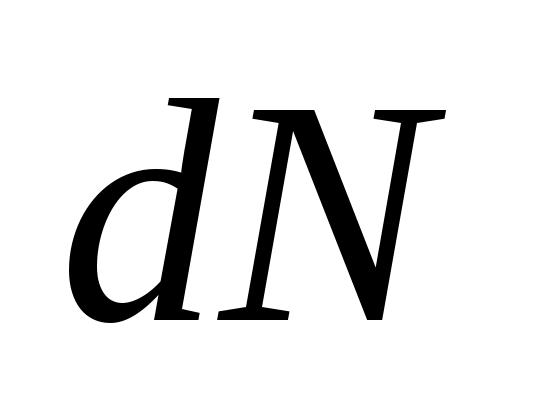 – число частиц). Отсюда индукция магнитного поля – число частиц). Отсюда индукция магнитного поля 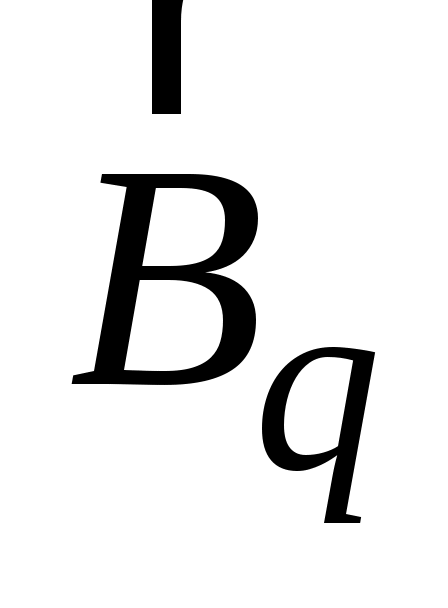 в точке А от одной заряженной частицы, находящейся на расстоянии r от точки А (рис. 13), будет равна в точке А от одной заряженной частицы, находящейся на расстоянии r от точки А (рис. 13), будет равна
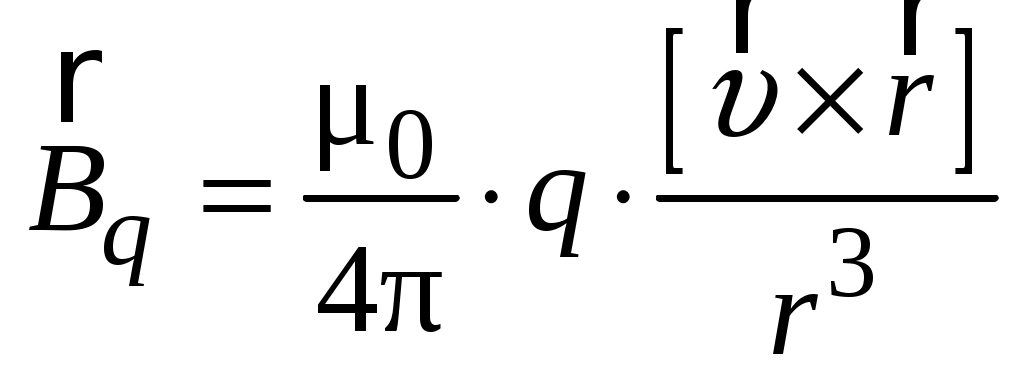 . (1.8) . (1.8)
Модуль магнитной индукции
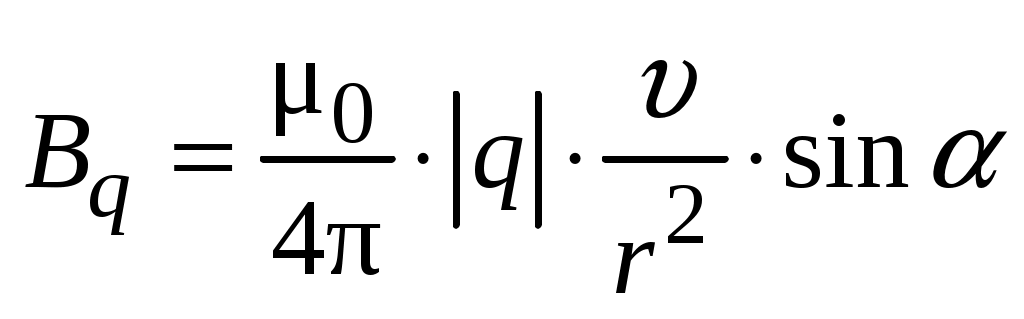 . (1.9) . (1.9)
Из (1.8) и (1.9) следует: неподвижная 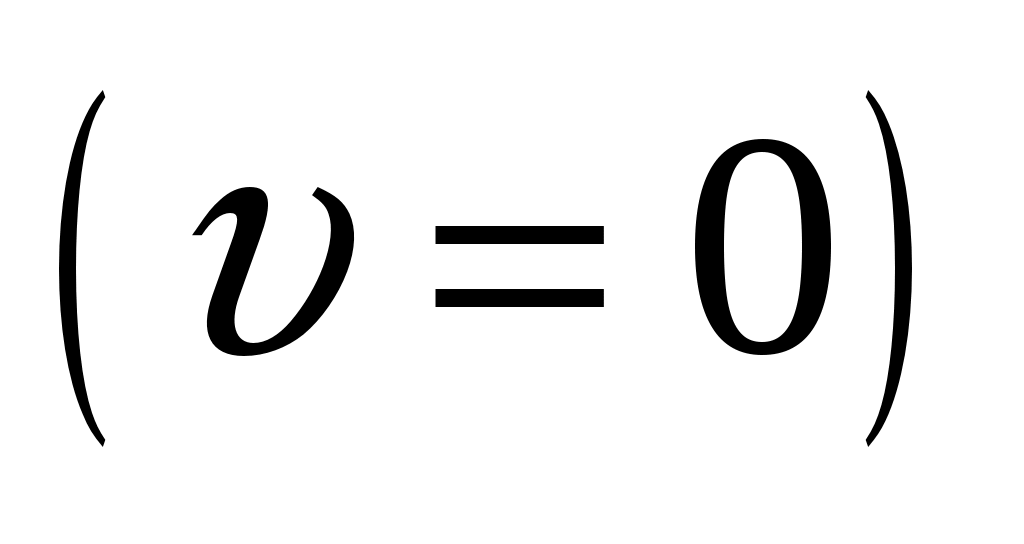 заряженная частица не создает магнитного поля ( заряженная частица не создает магнитного поля (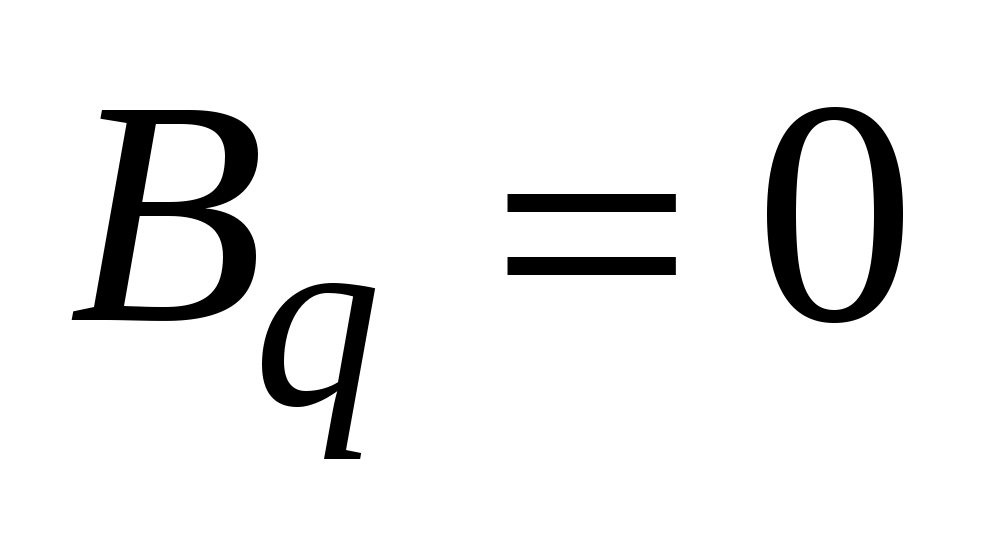 ); индукция магнитного поля обратно пропорциональна квадрату расстояния от заряженной частицы до рассматриваемой точки; индукция магнитного поля равна нулю на прямой, совпадающей с направлением скорости частицы ); индукция магнитного поля обратно пропорциональна квадрату расстояния от заряженной частицы до рассматриваемой точки; индукция магнитного поля равна нулю на прямой, совпадающей с направлением скорости частицы 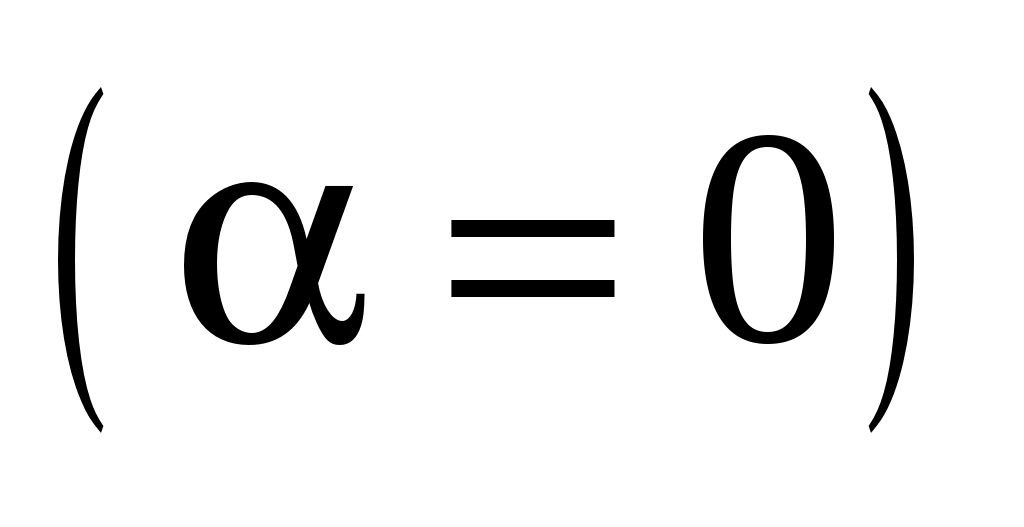 ; максимальное значение магнитной индукции имеет место в направлениях, ортогональных вектору ее скорости ; максимальное значение магнитной индукции имеет место в направлениях, ортогональных вектору ее скорости 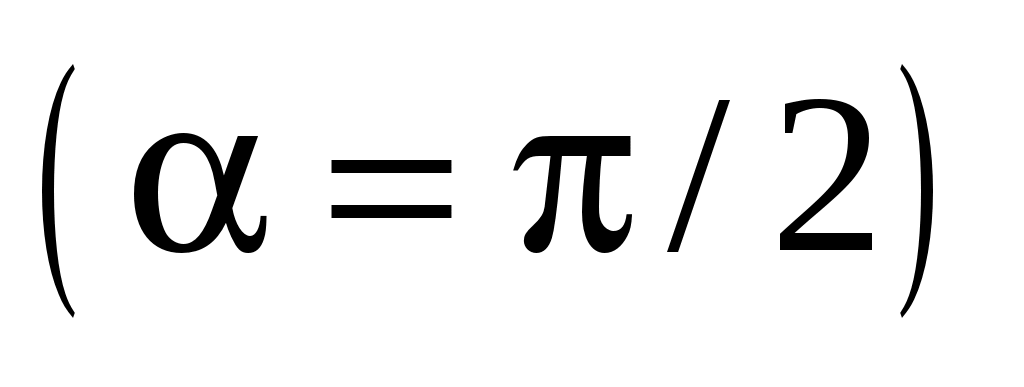 . .
Из выражения (1.8) следует, что вектор 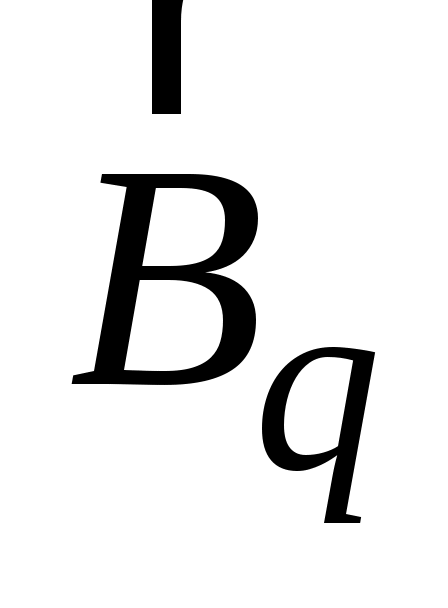 ортогонален плоскости, в которой находятся вектора ортогонален плоскости, в которой находятся вектора  и и 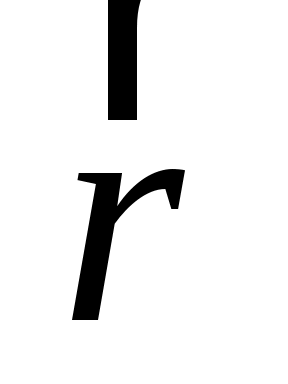 (рис. 13). Для частицы с положительным зарядом q направление вектора (рис. 13). Для частицы с положительным зарядом q направление вектора 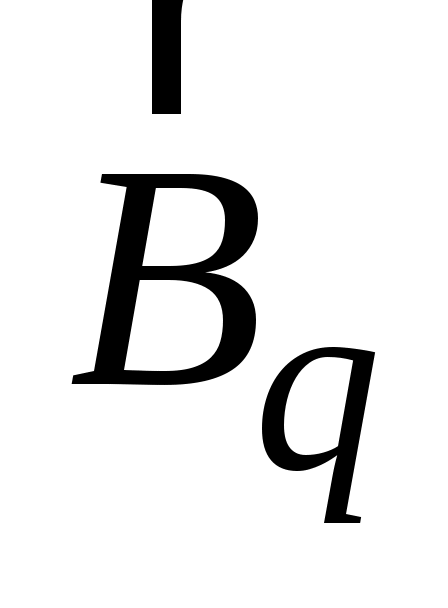 удобно определять по правилу правого винта: при ввинчивании буравчика в направлении скорости удобно определять по правилу правого винта: при ввинчивании буравчика в направлении скорости  конец ручки буравчика вращается в направлении линий магнитной индукции. При этом линии магнитной индукции представляют собой окружности, центры которых находятся на прямой ОС (рис. 13). Плоскости, в которых лежат линии магнитной индукции, перпендикулярны ОС. Одна из линий магнитной индукции показана на рис. 13. Если конец ручки буравчика вращается в направлении линий магнитной индукции. При этом линии магнитной индукции представляют собой окружности, центры которых находятся на прямой ОС (рис. 13). Плоскости, в которых лежат линии магнитной индукции, перпендикулярны ОС. Одна из линий магнитной индукции показана на рис. 13. Если 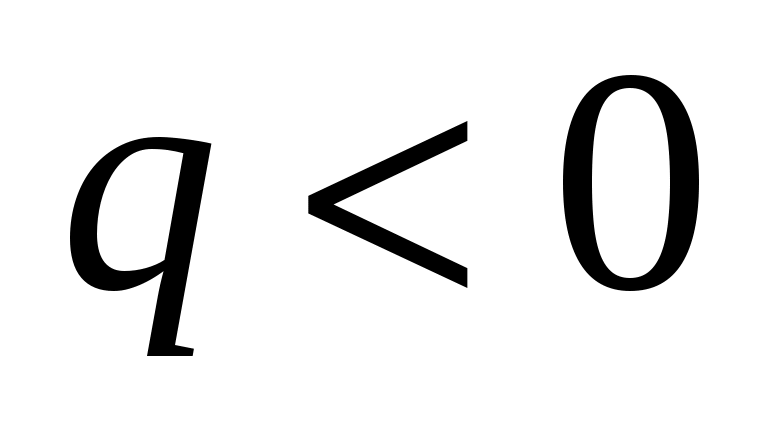 , то линии индукции имеют направление, противоположное указанному. , то линии индукции имеют направление, противоположное указанному.
При применении формулы (1.8) предполагается, что всякое изменение положения частицы в пространстве, а также величины и направления ее скорости  , мгновенно скажется на величине и направлении индукции , мгновенно скажется на величине и направлении индукции 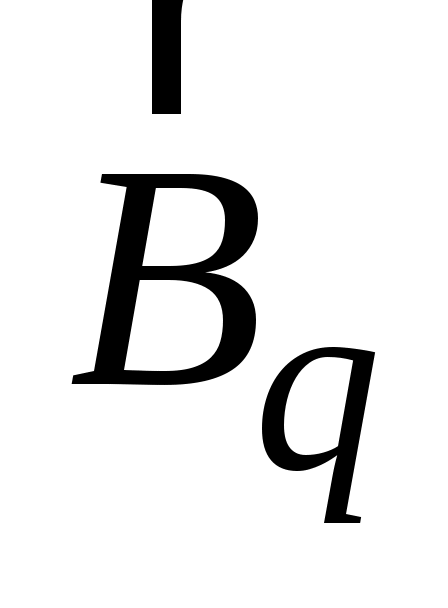 . В действительности это не так. Если частица изменила свое положение или скорость, то только через время . В действительности это не так. Если частица изменила свое положение или скорость, то только через время 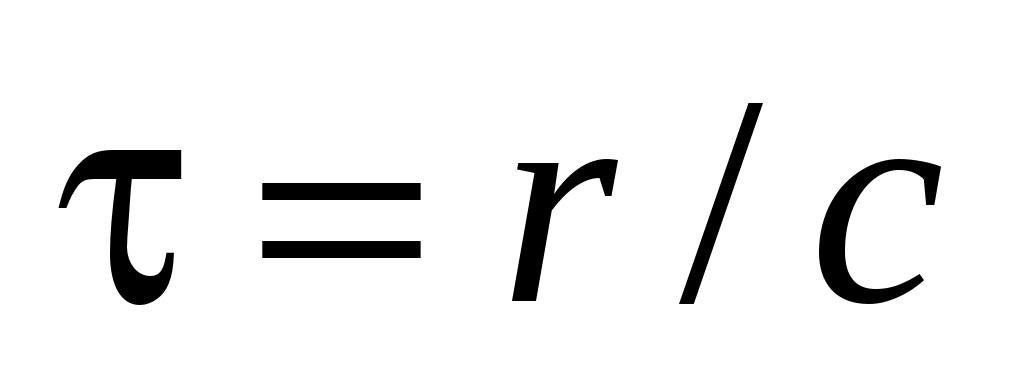 (τ – время запаздывания, (τ – время запаздывания, 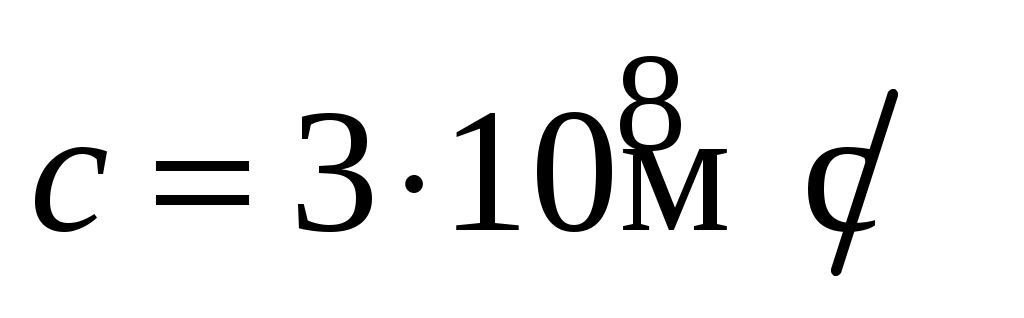 – скорость света) сигнал об этом дойдет до точки наблюдения. По этой причине (1.9) можно применять, если – скорость света) сигнал об этом дойдет до точки наблюдения. По этой причине (1.9) можно применять, если 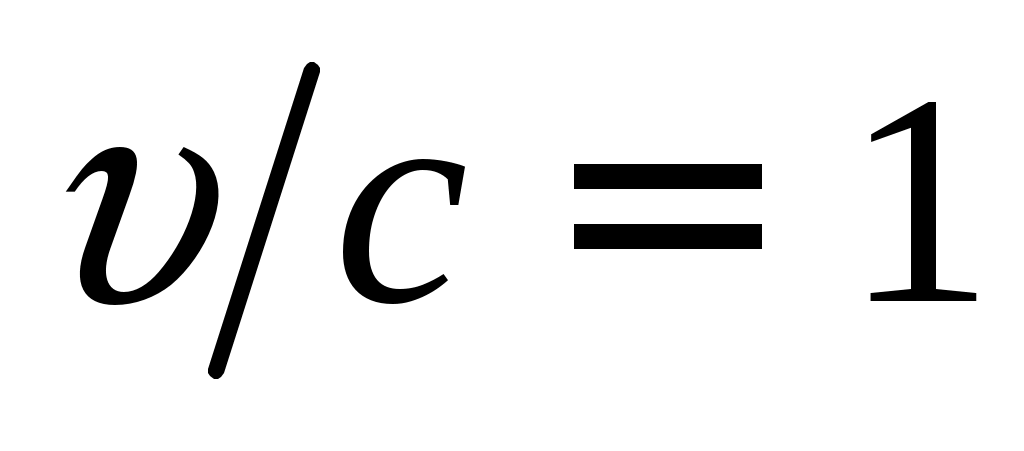 . .
|
 Скачать 2.73 Mb.
Скачать 2.73 Mb.