Био и Савар провели в 1820 г. исследование магнитных полей токов различной формы. Они установили, что магнитная индукция во всех случаях пропорциональна силе тока, создающего магнитное поле. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле тока I любой конфигурации может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.
Д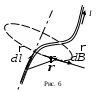 лина лина 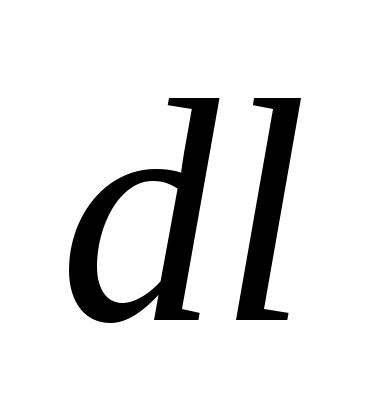 каждого участка тока настолько мала, что его можно считать прямым отрезком, расстояние от которого до точки наблюдения много больше каждого участка тока настолько мала, что его можно считать прямым отрезком, расстояние от которого до точки наблюдения много больше 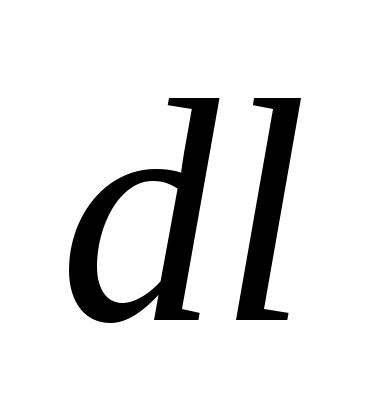 . Удобно ввести понятие элемента тока . Удобно ввести понятие элемента тока 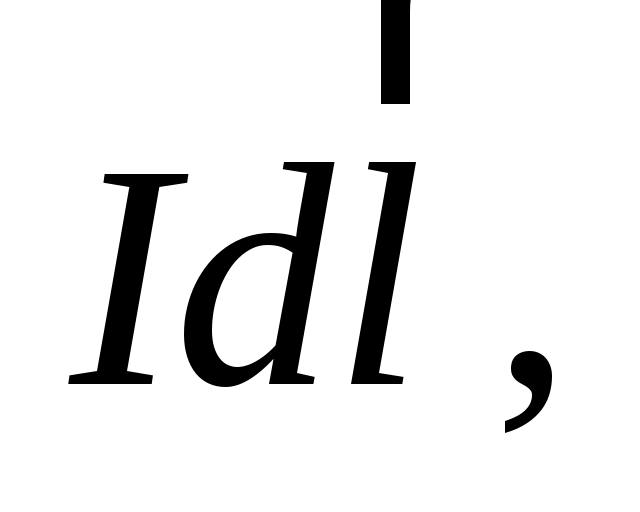 где направление вектора где направление вектора 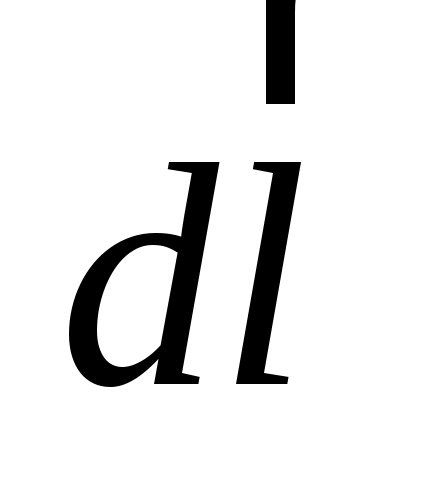 совпадает с направлением тока I, а его модуль равен совпадает с направлением тока I, а его модуль равен 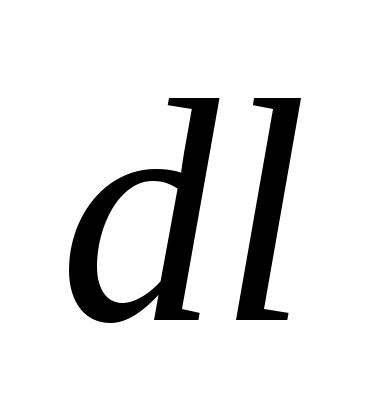 (рис. 6). (рис. 6).
Для индукции магнитного поля 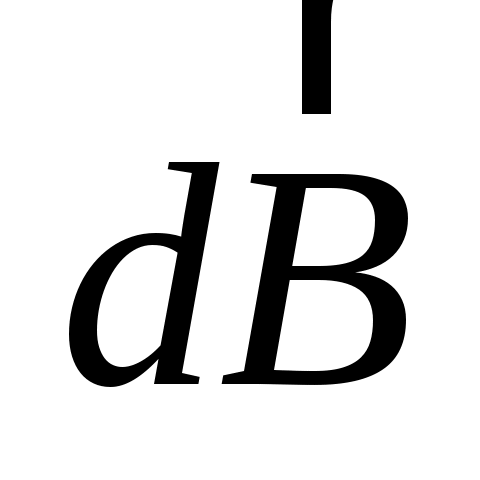 , создаваемого элементом тока , создаваемого элементом тока 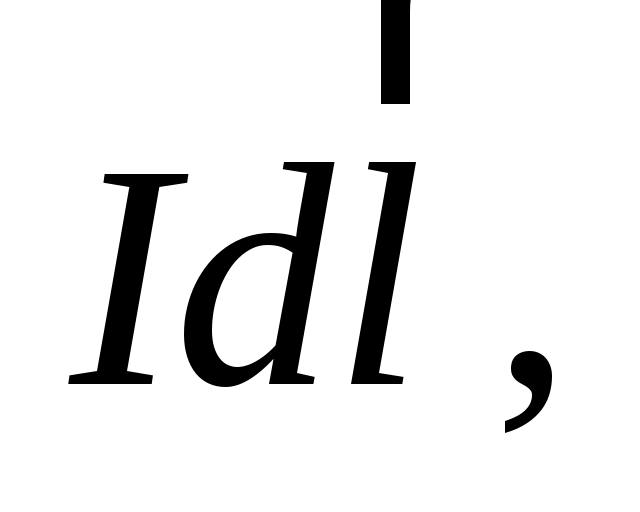 в точке, находящейся на расстоянии r от него (рис. 6), Лаплас вывел формулу, справедливую для вакуума: в точке, находящейся на расстоянии r от него (рис. 6), Лаплас вывел формулу, справедливую для вакуума:
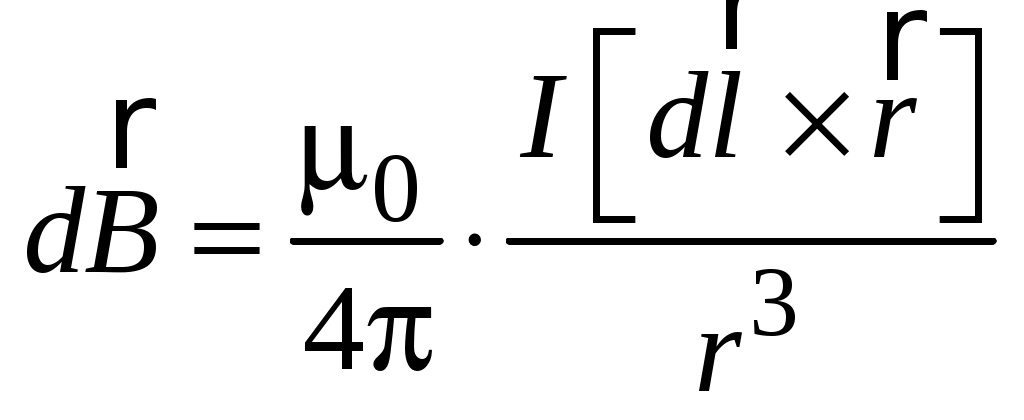 . (1.1) . (1.1)
Формула закона Био–Савара–Лапласа (1.1) написана в системе СИ, в которой постоянная 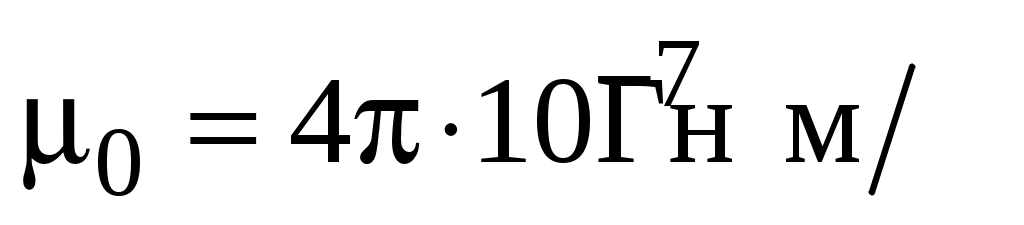 называется магнитной постоянной. называется магнитной постоянной.
Уже отмечалось, что в магнетизме, как и в электричестве, имеет место принцип суперпозиции полей, т. е. индукция магнитного поля, создаваемого системой токов, в данной точке пространства равна векторной сумме индукций магнитных полей, создаваемых в этой точке каждым из токов в отдельности:
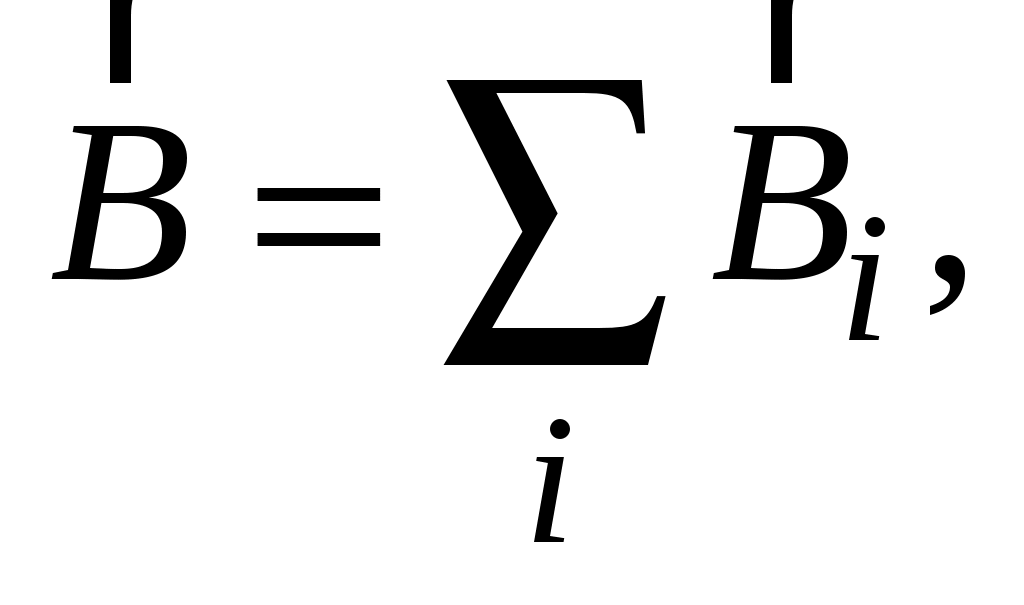 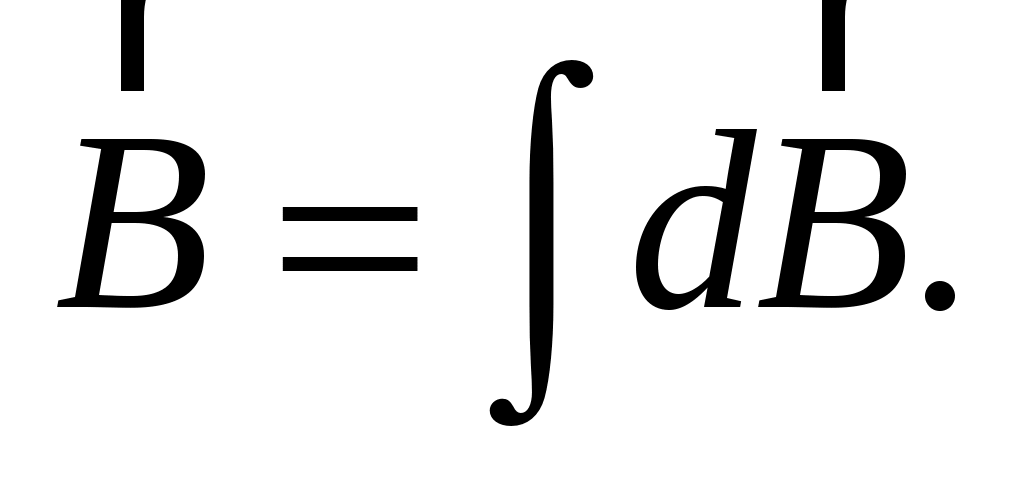 (1.2) (1.2)
Н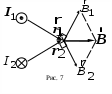 а рис. 7 приведен пример построения вектора магнитной индукции а рис. 7 приведен пример построения вектора магнитной индукции 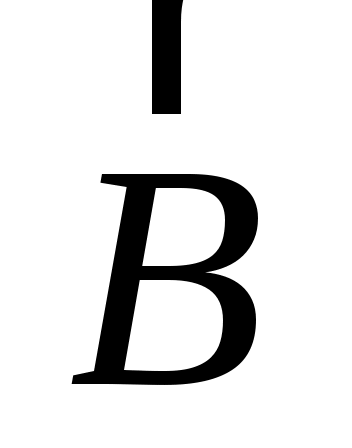 в поле двух параллельных и противоположных по направлению токов в поле двух параллельных и противоположных по направлению токов 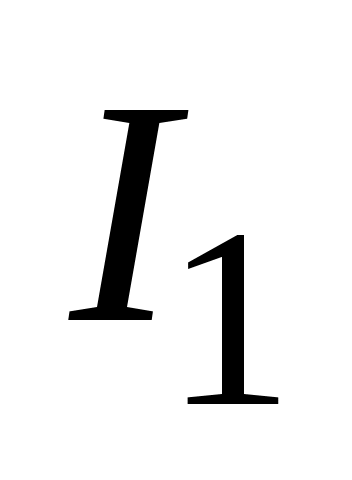 и и 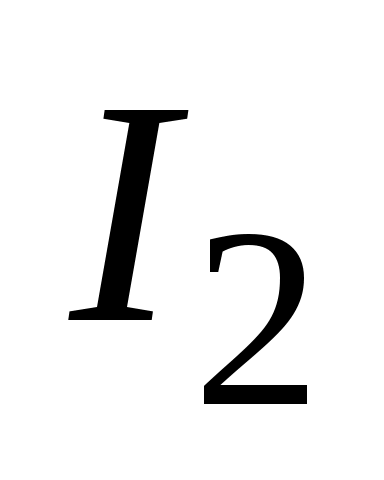 : : 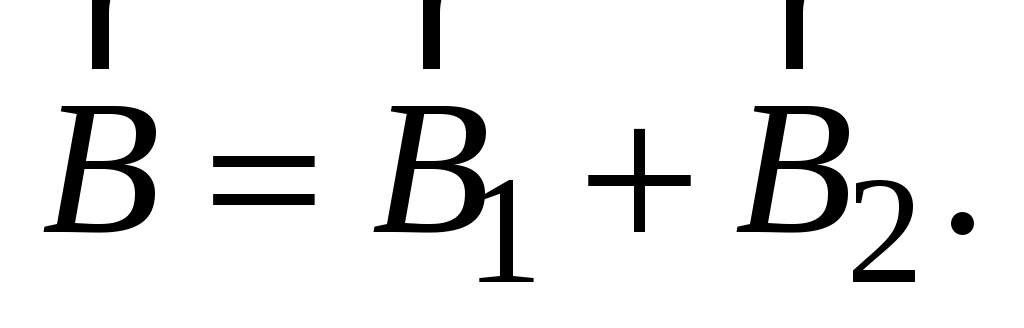 
1.3. Применение закона Био–Савара–Лапласа.
Магнитное поле прямого тока
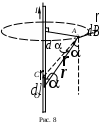
Рассмотрим отрезок прямого тока. Элемент тока 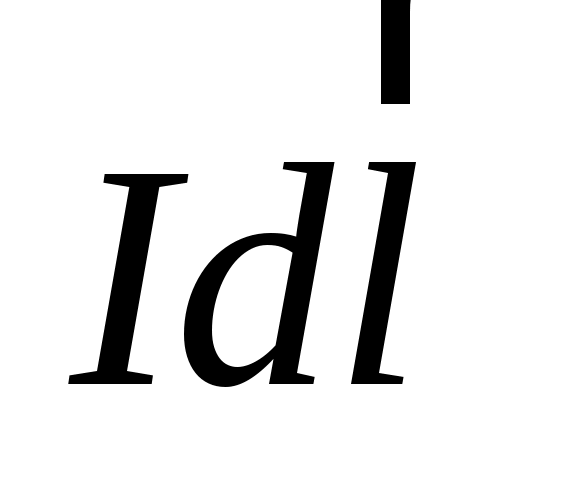 создает магнитное поле, индукция которого в точке А (рис. 8) по закону Био–Савара–Лапласа находится по формуле: создает магнитное поле, индукция которого в точке А (рис. 8) по закону Био–Савара–Лапласа находится по формуле:
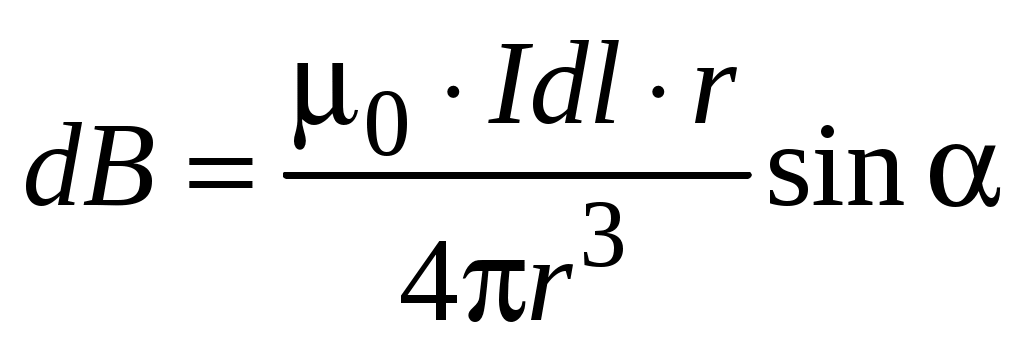  , (1.3) , (1.3)
где 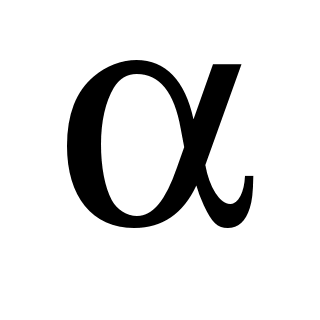 – угол между направлением тока и вектором – угол между направлением тока и вектором 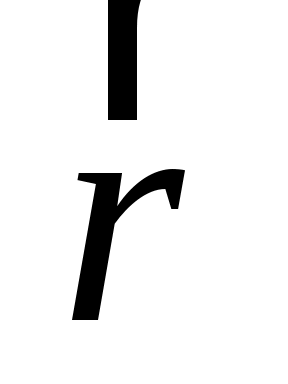 , характеризующим положение точки А относительно , характеризующим положение точки А относительно 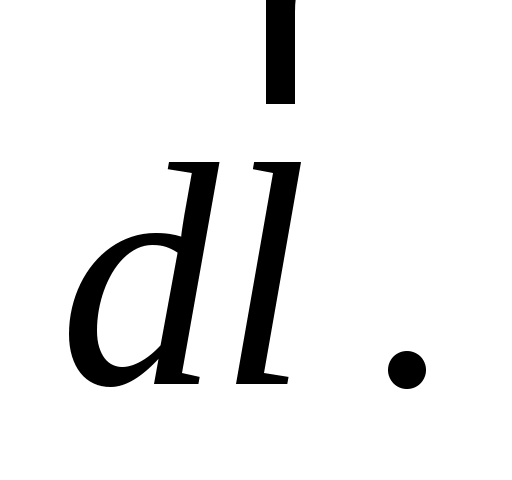
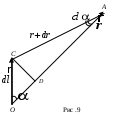
На рис. 9 представлен фрагмент рис. 8. Опустив перпендикуляр из точки С на сторону ОА, получим два прямоугольных треугольника. Из треугольника ODC следует, что СD=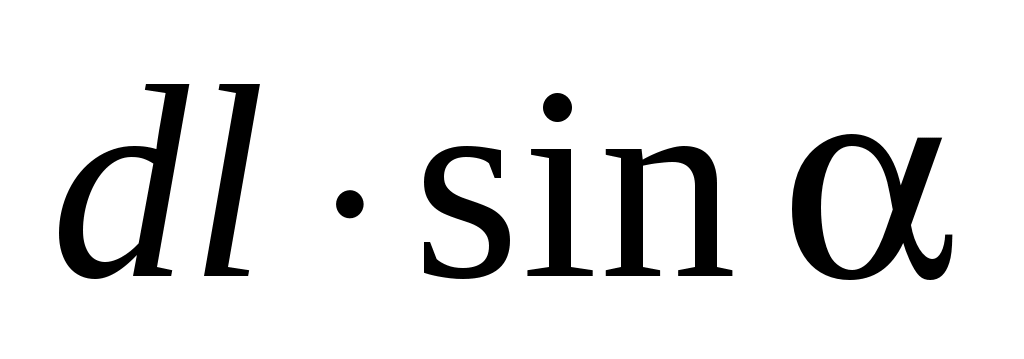 , а из треугольника CDA следует, что CD= , а из треугольника CDA следует, что CD=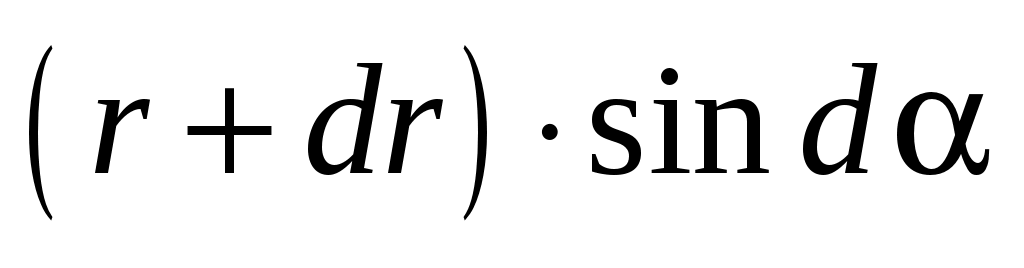 . .
Учитывая, что 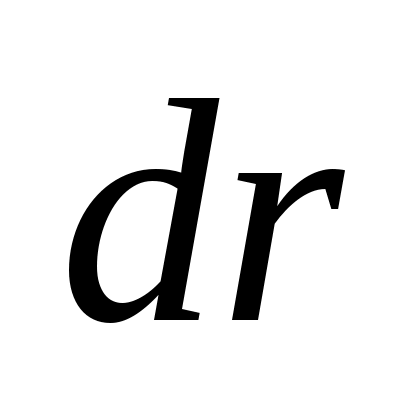 и и 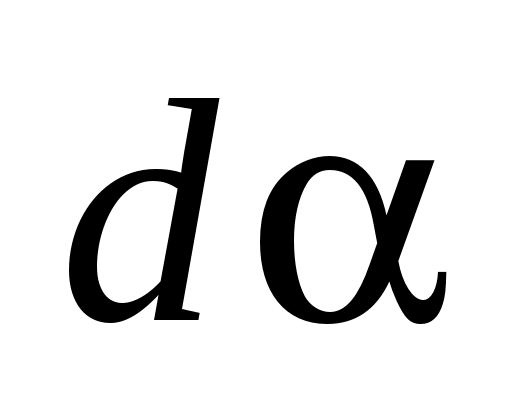 бесконечно малые величины, получим бесконечно малые величины, получим
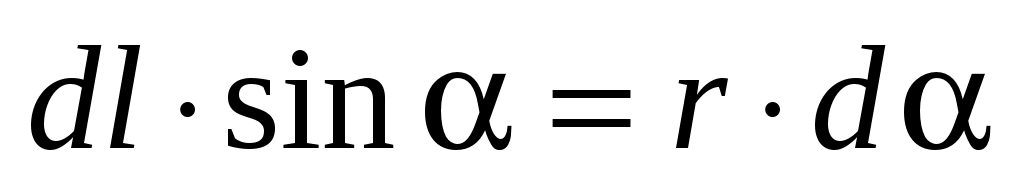 . (1.4) . (1.4)
После подстановки (1.4) в (1.3) получим:
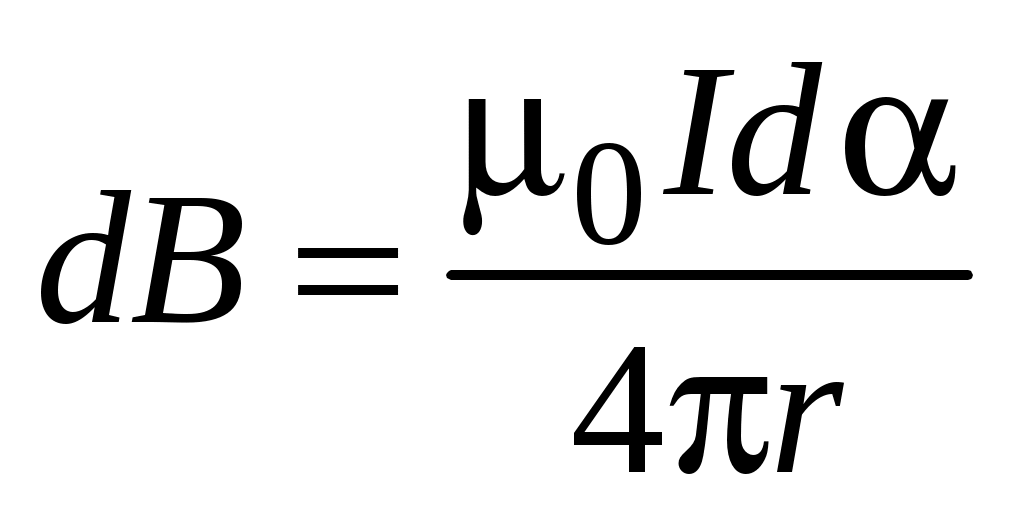 . .
Из рис. 8 следует, что 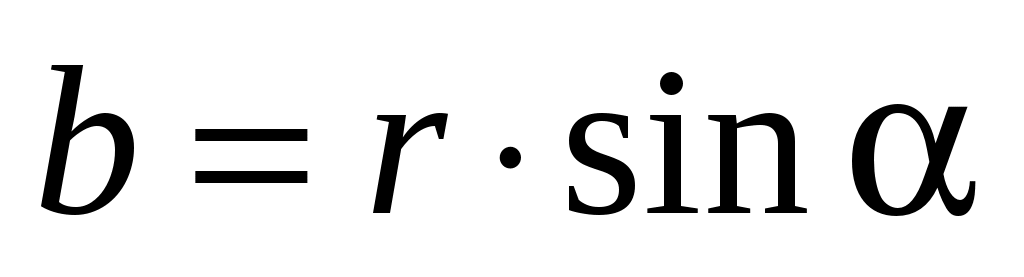 , где b – расстояние от прямого тока до рассматриваемой точки А. Следовательно, , где b – расстояние от прямого тока до рассматриваемой точки А. Следовательно,
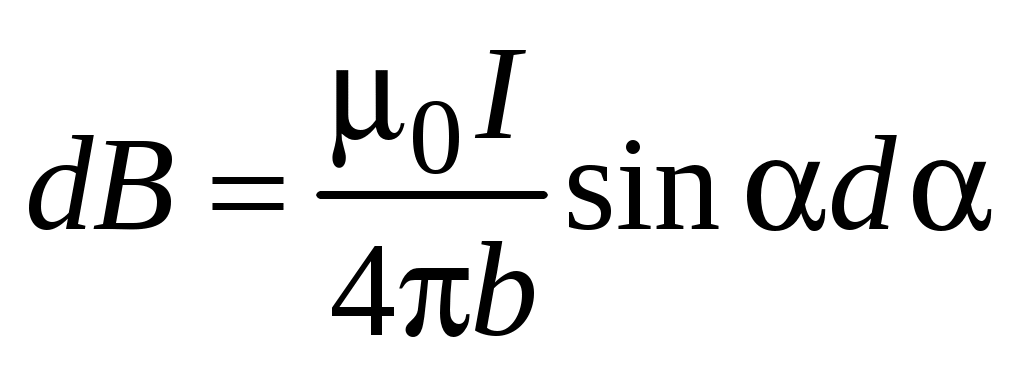  . .
По принципу суперпозиции 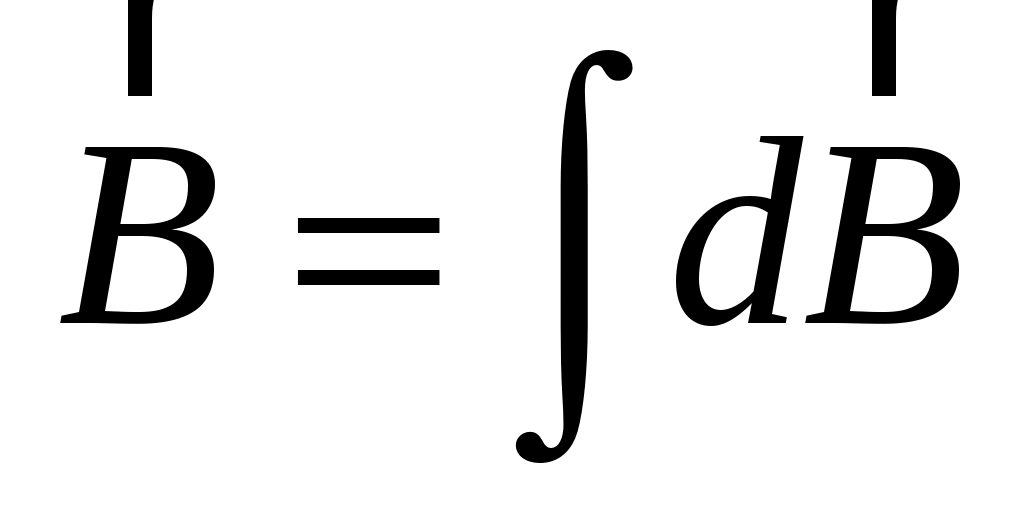 . В точке А все . В точке А все 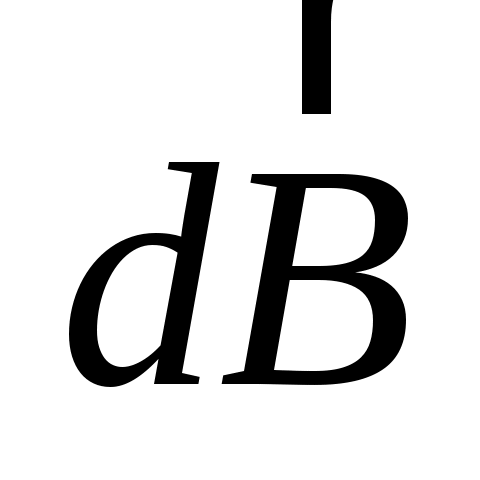 от различных элементов отрезка прямого тока имеют одинаковое направление. Величина магнитной индукции в точке А равна алгебраической сумме от различных элементов отрезка прямого тока имеют одинаковое направление. Величина магнитной индукции в точке А равна алгебраической сумме  от всех элементов прямого тока: от всех элементов прямого тока:
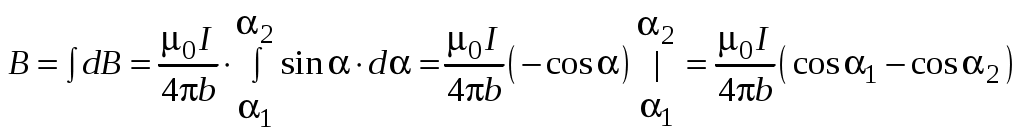
I
.
Т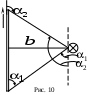 аким образом, для индукции магнитного поля отрезка прямого тока конечной длины (рис. 10) получаем формулу аким образом, для индукции магнитного поля отрезка прямого тока конечной длины (рис. 10) получаем формулу
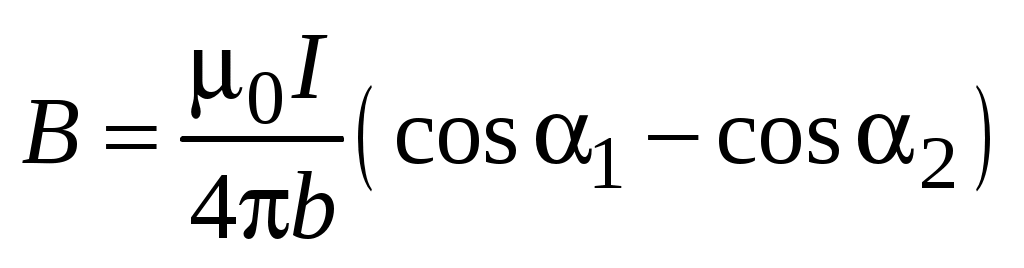 . (1.5) . (1.5)
В случае бесконечно длинного прямого проводника с током 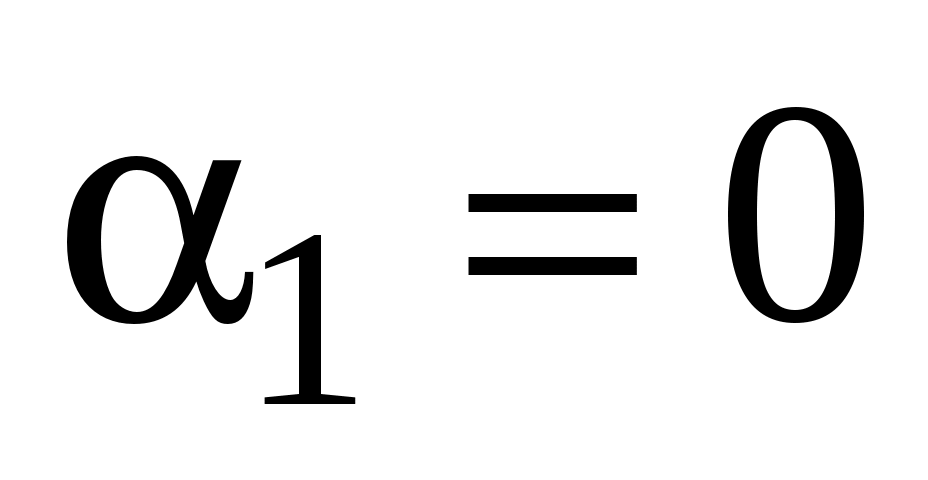 , , 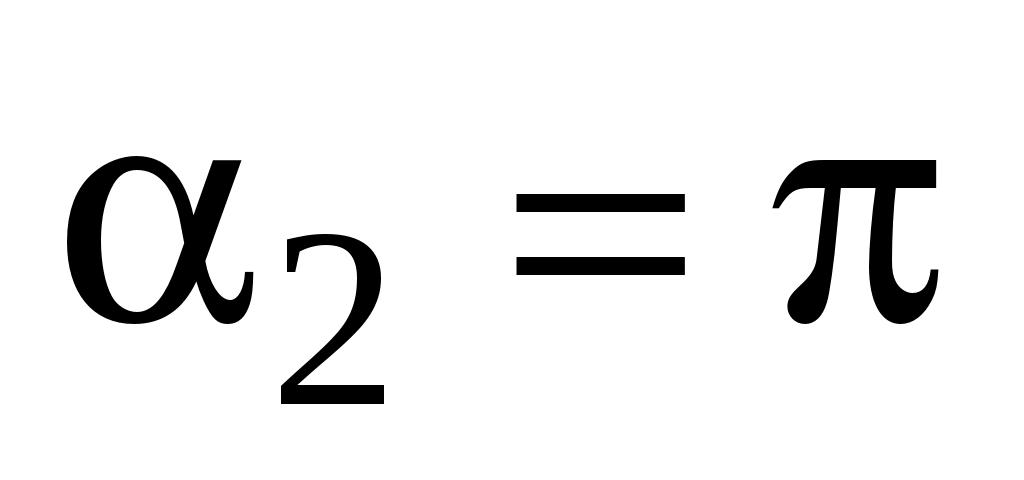 . Следовательно, . Следовательно, 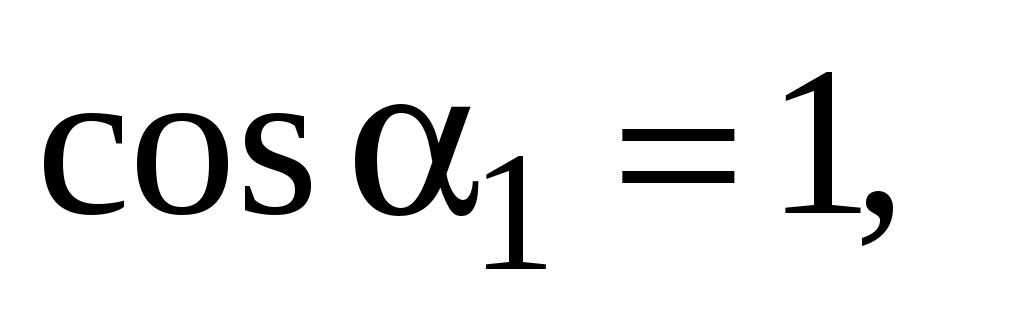 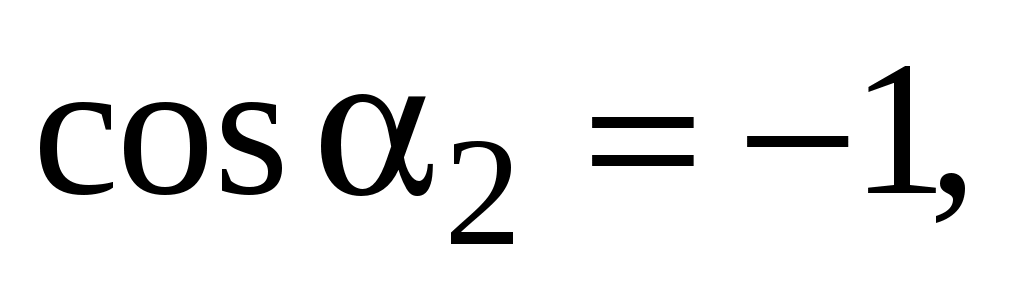 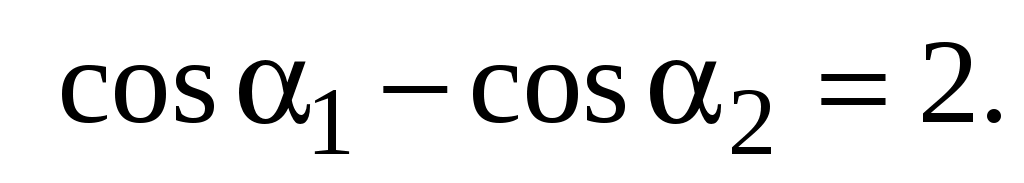 Отсюда следует, что индукция магнитного поля бесконечно длинного прямого проводника с током находится по формуле Отсюда следует, что индукция магнитного поля бесконечно длинного прямого проводника с током находится по формуле
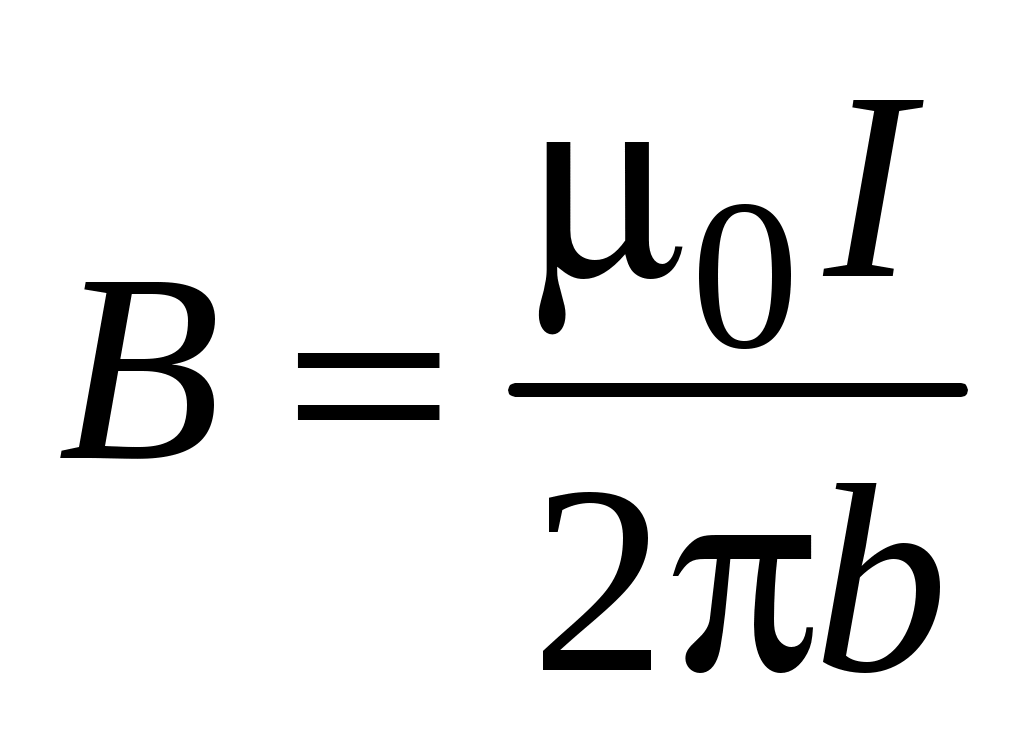 . (1.6) . (1.6)
|
 Скачать 2.73 Mb.
Скачать 2.73 Mb.