Магнетизм

• Название: Магнетизм
• Дата: 23.11.2022
• Размер: 2.73 Mb.
• Имя файла: physics_bookshelf_magnetics_andreev_chernykh.doc
• Тип: Конспект; #807013
• страница: 6 из 17

1.7. Применение теоремы о циркуляции вектора магнитной индукции. Магнитное поле внутри прямого проводника с током

В качестве примера применения теоремы о циркуляции вектора магнитной индукции для расчета индукции магнитного поля рассмотрим магнитное поле постоянного тока, текущего в бесконечно длинном прямом проводнике цилиндрической формы радиуса R. Замкнутый контур выберем в виде окружности радиуса r, лежащей в плоскости, перпендикулярной оси проводника, и с центром на этой оси (рис. 18).

Пусть направление обхода контура связано с направлением тока правилом правого винта. Из осевой симметрии следует, что во всех точках, равноудаленных от оси проводника с током, индукция магнитного поля одинакова. Проекция вектора магнитной индукции на направление элементарного перемещения совпадает по величине с магнитной индукцией во всех точках замкнутого контура.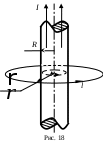

Таким образом, для циркуляции вектора магнитной индукции получаем

, (1.12)

где – проекция вектора магнитной индукции на направление элементарного перемещения .

Если , то по закону полного тока:

. (1.13)

Из сравнения (1.12) и (1.13) следует

,

что совпадает с ранее полученной формулой (1.6).

Если , в предположении равномерного распределения тока по сечению проводника, по закону полного тока

, (1.14)

где – площадь, охватываемая контуром l; j – плотность тока. Из сравнения (1.12) и (1.14) следует

. (1.15)

На графике (рис. 19) показана зависимость индукции магнитного поля от расстояния до оси прямого проводника с током.



Рассмотрим полый проводник цилиндрической формы в виде трубы, вдоль стенки которой течет постоянный ток. Пусть R – радиус трубы. Замкнутый контур выберем также в форме окружности радиуса r с центром на оси проводника. Пусть . В этом случае контур не охватывает ток и

. (1.16)

Из сравнения (1.12) и (1.16) следует, что магнитное поле внутри полого проводника с током отсутствует. На рис. 20 представлена зависимость величины индукции магнитного поля в некоторой точке от ее расстояния до оси прямого полого проводника с током.

1.8. Магнитное поле соленоида

Соленоид представляет собой тонкий провод, навитый плотно (виток к витку) на цилиндрический каркас. На рис. 21 представлено схематическое изображение бесконечно длинного соленоида диаметром D. Будем считать, ч 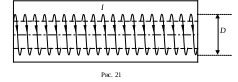то намотка выполнена плотно, соседние витки прилегают друг к другу и по соленоиду течет ток силой I.

Выясним, как направлен вектор в 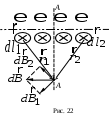различных точках магнитного поля соленоида. Для этого рассмотрим два любых элемента тока и , равных по величине и расположенных симметрично относительно плоскости сечения АА, перпендикулярной к оси соленоида (рис. 22). Элементы и перпендикулярны плоскости рисунка.

П о закону Био–Савара–Лапласа рассматриваемые элементы тока создадут в каждой точке сечения АА магнитные поля, индукции которых и равны по величине, а их результирующий вектор параллелен оси соленоида.

Этот вывод справедлив для любой пары одинаковых элементов тока соленоида, расположенных симметрично относительно плоскости сечения АА. Из принципа суперпозиции следует, что линии индукции магнитного поля бесконечно длинного соленоида, если оно отлично от нуля, должны быть параллельны оси соленоида как внутри, так и вне соленоида.

Теперь докажем, что в точках, находящихся на расстоянии, много большем диаметра соленоида с плотной намоткой витков, магнитное поле равно нулю. Для этого рассмотрим два равных по модулю элемента тока и , расположенных симметрично относительно оси соленоида (рис. 23).

В точках, достаточно удале 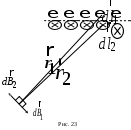нных от соленоида, для которых , по закону Био–Савара–Лапласа магнитные индукции и будут равны и противоположны по направлению с хорошей степенью точности. Этот вывод справедлив для любой пары одинаковых элементов тока соленоида, расположенных симметрично относительно оси соленоида. Из принципа суперпозиции следует, что в достаточно удаленных от соленоида точках магни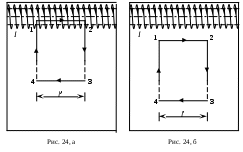тное поле отсутствует.

Д ля вычисления величины индукции магнитного поля соленоида применим теорему о циркуляции вектора по замкнутому контуру. Выберем контур прямоугольной формы, две стороны которого параллельны, а другие две стороны перпендикулярны оси соленоида (рис. 24, а, б).

Пусть участок контура находится от соленоида на расстоянии, много большем его диаметра, а участок , параллельный оси соленоида, расположен в первом случае внутри соленоида (рис. 24, а) и во втором случае вне соленоида (рис. 24, б).

Циркуляция вектора на контуре 1–2–3–4 равна сумме линейных интегралов:

.

Из соображений симметрии и так как линии магнитной индукции должны быть параллельны оси соленоида, как было показано выше, во всех точках участка . На участках контура и перпендикулярен элементарному перемещению. Следовательно, во всех точках участков и . Точки участка находятся на расстоянии, много большем диаметра соленоида, и в них, как отмечалось ранее, можно считать с хорошей степенью точности.

Таким образом,

, (1.17)

где – длина участка .

Согласно теореме о циркуляции в случае, когда контур охватывает ток (рис. 24, а),

, (1.18)

где n – плотность намотки (число витков на единицу длины соленоида),
а n – число витков на длине . Если контур не охватывает ток (рис. 24, б), то

. (1.19)

Из сравнения (1.17) с (1.18) и (1.19) следует, что магнитное поле внутри бесконечно длинного соленоида однородно. Магнитная индукция поля равна

. (1.20)

Поле вне соленоида отсутствует.