МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ. Математическая логика

• Название: Математическая логика
• Анкор: МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ.doc
• Дата: 05.04.2018
• Размер: 1.08 Mb.
• Имя файла: МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕОРИЯ АЛГОРИТМОВ.doc
• Тип: Документы; #17626
• Категория: Математика
• страница: 1 из 8

МАТЕМАТИЧЕСКАЯ ЛОГИКА

Математическая (теоретическая, символьная) логика – нормативная наука о формах и приемах интеллектуальной познавательной деятельности, осуществляемой с помощью искусственных (формальных и формализованных) языков. Иначе, математическая логика – анализ рассуждений (в первую очередь, их формы, а не содержания).

Основными разделами математической логики является: логика высказываний, логика предикатов, металогика.
Логика высказываний, как и логика предикатов, имеет два аспекта: семантический, когда она является содержательной теорией логических отношений между суждениями; синтаксический, когда логика является методом дедуктивной формализацией содержательных теорий.

Замечание.

1. 
   Согласно П.Г.Порецкого математическая логика есть логика по предмету, математика по методу, а согласно Г.Фреге математическая логика изучает логику математики путем ее дедуктивной формализации.
   
2. 
   Математическая логика есть современный этап в развитии формальной логики – науки о построении правильных заключений (доказательств, опровержений) чисто формальным путем, когда исходят из вида (логической формы) посылок, а не их содержания.
   
3. 
   Логика, в отличие от математики (изучающей количественные отношения и пространственные формы) изучает не количественные отношения между объектами.
   
4. 
   Математическая логика пришла на смену традиционной(описательной) формальной логике во 2-ой половине 19в.-начале 20 века.
   
5. 
   Познание объясняется следующим деревом:
   

Познание

(процесс гомоморфного отображения действительности)

дедукция

индукция

аналогия

Логические приемы оперирования с формами познания

Приемы интеллектуального (рационального, языкового) познания

Способы познания

Чувственные формы познания


Рациональные формы познания

ощущение

восприятие

представление

понятия

высказывание

теории

Логические приемы образования форм познания

6. 
   Основными объектами математической логики являются: высказывания и логические процедуры. Поскольку все научные знания, процессы управления и др. формулируются, как последовательность утвердительных повествовательных предложений (т.е. высказываний субъектно-предикатной структуры).
   
7. 
   Науки, предложения которых преимущественно получаются как следствия некоторых общих принципов, постулатов, аксиом, принято называть дедуктивными, а аксиоматический метод, посредством которого выводы этих частных предложений, часто называют аксиоматико-дедуктивными.
   
8. 
   Основная задача логики – отделение правильных схем рассуждения (умозаключения, доказательств – мыслительного процесса, в ходе которого из одного или нескольких суждений, называемых……., выводится новое суждение, называемое заключением или следствием) от неправильных и систематизации первых.
   

ПАРАДИГМЫ ФОРМАЛЬНОЙ ЛОГИКИ.

1. 
   Правильность рассуждения (умозаключения, вывода, доказательства) зависит только от его формы и не зависит то его конкретного содержания.
   
2. 
   Истинность и правильность мышления суть различных объектов:
   
   • 
     истинность характеризует рассуждение в его отношении к действительности;
     
   • 
     правильность характеризует рассуждение в его отношении к законам и правилам логики.
     

Пояснение. Различие между истинностью и правильностью отчетливо видно в тех случаях, когда формально правильное рассуждение приводит к логическому высказыванию.

Пример. Все металлы – твердые тела.

Ртуть – не твердое тело.

Ртуть - не металл.

Это правильное умозаключение логично (из-за логики первой посылки).
ПРЕДМЕТ, ЦЕЛЬ, ЗАДАЧИ И СОДЕРЖАНИЕ ЧИТАЕМОГО КУРСА ЛЕКЦИЙ.

Предметом читаемого курса являются функциональные и формальные системы логики: алгебры логики (высказываний и предикатов), классические и неклассические исчисления высказываний и предикатов, метатеория логических исчислений.

Целого преподавания дисциплины будущим инженерам в области ВТ является овладение студентами основами синтеза и анализа дискретных структур методами алгебры логики и логических исчислений.

Задачи дисциплины:

• 
  освоение предметных языков логики высказываний и логики предикатов;
  
• 
  приобретение навыков использования дедуктивных методов вывода заключений из посылок;
  
• 
  умение работать с различными моделями формального уточнения понятия “алгоритм”.
  

Содержание читаемого курса представим следующим деревом:


Математическая логика

F.S=

Прикладные исчисления

_п=< L(_в), D(_в)>

_B=< L(_B), D(_B)>

Классическое _п

Классическое _В

неклассическое _п

неклассическое _В

Многозначное _В

Логическое исчисление


А_B

А_П

А=
Метатеория логических исчислений


Здесь:

А=
F.S= - формальная система (т.е. построение математической логики, как теории, является чисто синтаксическим объектом);

 - исчисление ( _в - исчисление высказываний; _п - исчисление предикатов);

L – язык (L(_в) – язык исчисления высказываний, L(_п) – язык исчисления предикатов), т.е. множество синтаксически правильно построенных выражений(формы F).

D – дедуктивные средства (D(_в) – дедуктивные средства исчисления высказываний, D(_п) – дедуктивные средства исчисления предикатов);

А_B = < B, B²  - алгебра логики высказываний;

А_B = < Р_(Х1, …, _Хn),  ,B²,  - алгебра логики предикатов.

Примечание. В том случае, если между морфологическими элементами формальной системы F.S. и элементами содержательной системы А существует функциональная биекция, то все исходные

положения F.S. получают интерпретацию. Говорят, что интерпретированная F.S. есть язык, описывающий ту или иную предметную область.

МЕСТО ЧИТАЕМОГО КУРСА О ЗАКОНАХ И ФОРМАХ ПРАВИЛЬНОГО МЫШЛЕНИЯ.

Логика


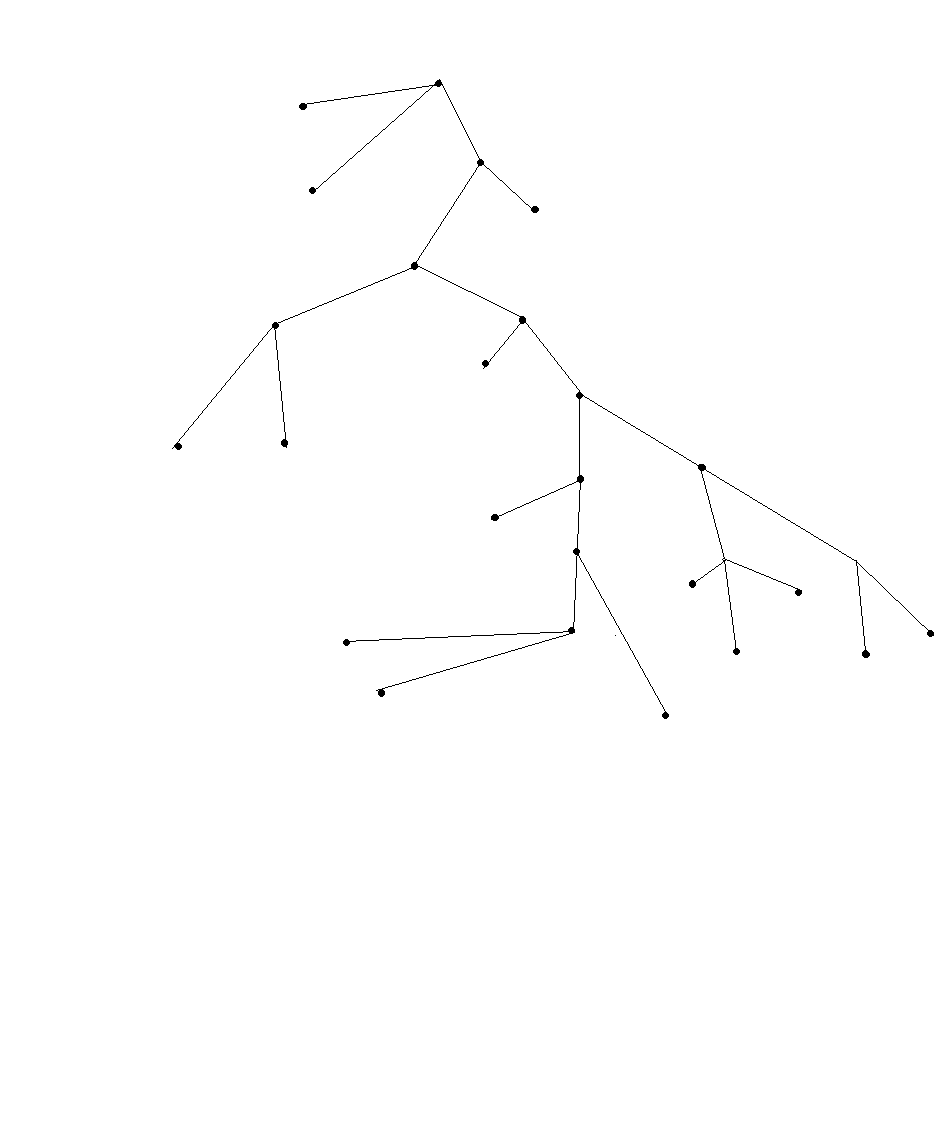
Диалектическая логика

Дедуктивные (достоверные) логики

Металогика (методология дедуктивных наук)

Формальная логика (наука о законах выводного знания)

Индуктивные (правдоподобные) логики

Математическая (теоретическая) логика

Нечеткая логика

Традиционная (описательная)

логика


Античная логика

Четкая логика

Классическая логика

Конечнозначные

логика

Неклассические логики

Бесконечнозначные логика

Счетнозначная логика

Вероятностная логика

Функциональные системы

Формальные

системы

Алгебра логики предикатов

Алгебра логики высказываний

метатеории

исчисления

Пояснения к этому дереву сделаем следующие:

1. 
   Предмет логики (по Аристотелю – средство обоснования истины) отличается от предмета всех других наук тем, что она(логика) исследует не закономерности объективного мира (природы, общества), чем занимаются естественные науки (физика, химия, биология) и общественно-политические науки (история, социология), а законы и формы логического мышления, оставляя в стороне описание фактического процесса протекания мышления по законам причинного следования (это предмет психологии).
   

Для уяснения приведенного выше отметим, что следует отличать мышление человека как объект изучения и как среду познания окружающего мира, т.е.


Мышление человека

Мышление как объект изучения.

Науки, изучающие мышление

логика

Мышление как познание объективного мира

Науки, изучающие объективный мир

Естественные науки

Общественно-политические науки

Философия, физиология, психология, кибернетика.

Умозаключения в логике делят на дедуктивные и индуктивные.

2. 
   Дедукция – переход от общего к частному по правилам логического вывода, позволяющие получить из истинных посылок(известных знаний) истинное заключение (новое знание, т.е. выводное знание).
   
3. 
   Индукция – переход от частного к общему. В отличии от дедуктивных рассуждений(построений) индукция не гарантирует истинного заключения при истинности посылок. Принято дедуктивную логику называть достоверной, а индуктивную логику – правдоподобной (проблемотичой). Деление выводов(умозаключений в традиционной логике) в современной логике на правильные и неправильные означает различие отношения логического следования на два вида – дедуктивные и индуктивные.
   
4. 
   Формальная логика – наука о законах выводного знания, т.е. знания, полученного из раннее установленных и проверенных истин (без обращения в каждом конкретном случае к опыту) только с помощью законов и правил логического мышления. В соответствии с основным принципом логики правильность рассуждения (умозаключения, доказательства, вывода) зависит только от его формы и не зависит от его конкретного содержания.
   
5. 
   Традиционная (описательная) логика, как совокупность………….., изучает общечеловеческие законы правильного построения и сочетания мыслей в рассуждениях, общечеловеческие формы мыслей (понятия, суждения) и формы умозаключений, а также средства мысли (определения, как отношения между понятиями; принципы образования понятий; суждений, умозаключений),необходимых для рационального (языкового) познания в любой области человеческой деятельности.
   
6. 
   Математическая логика (как современный этап развития формальной логики) изучает логику содержательных теорий (т.е. множество взаимосвязанных понятий и высказываний, замкнутое относительно логической выводимости) средствами математики, а логику самой математики – с помощью различного рода исчислений.
   

Замечание. Отличие математики от логики поясним вопросами, ответы на которые они ищут.


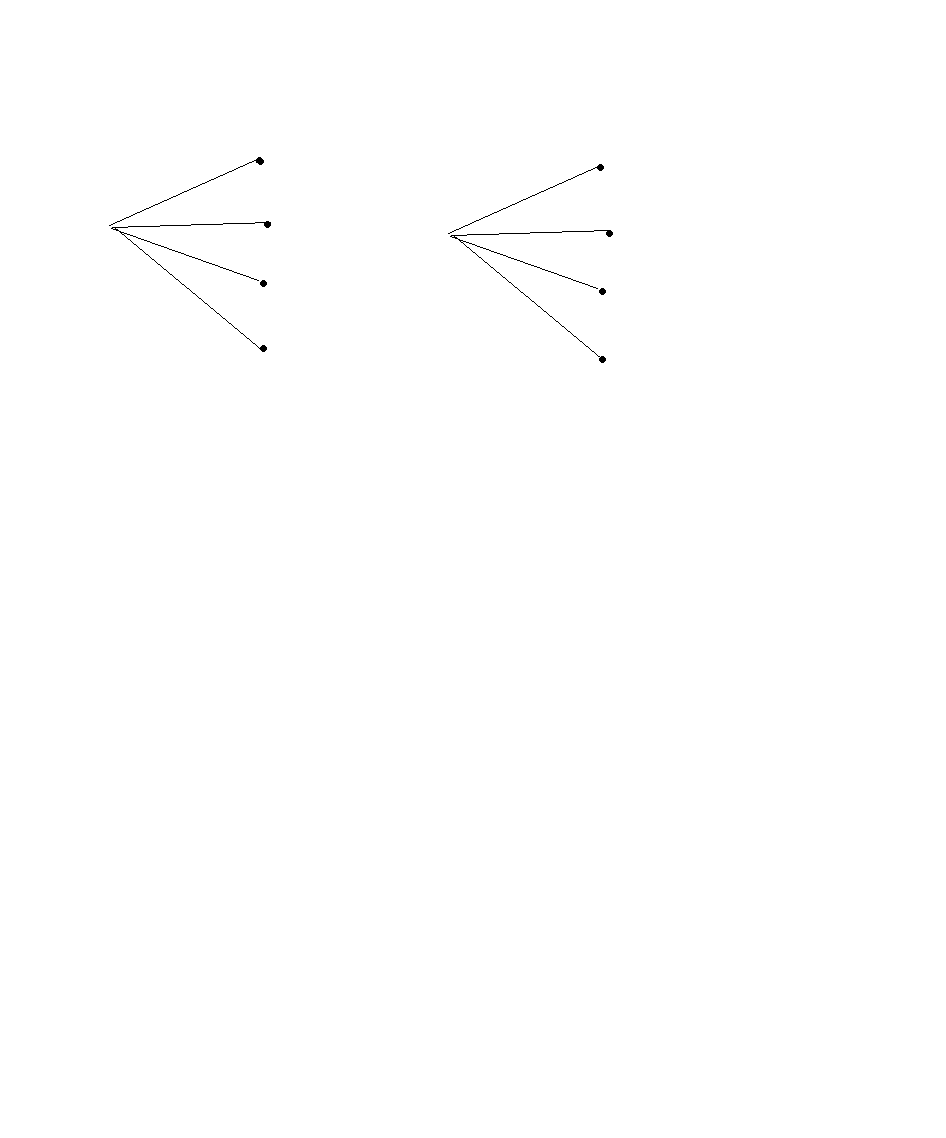
Вопросы математики

Сколько?

Как далеко?

Как долго?

(т.е. вопросы о количественных отношениях)

Вопросы логики

Что это значит?

Есть ли противоречие в этом суждении?

Каковы основания этого доказательства?

(т.е. вопросы о неколичественных отношениях)

7. 
   Нечеткая логика – логика, истинностные значения высказывания которой интерпретируются нечетким подмножеством заданного множества значений.
   
8. 
   Четкая логика – логика, в которой для интерпретации высказываний используется множество истинностных значений М. Говорят, что логика называется:
   

• 
  классической (двузначной), если |M|=2, т.е. М={0,1} или М={U,};
  
• 
  неклассической (многозначной), если |M|>2;
  
• 
  бесконечнозначной, если |M|=N (это т. н. счетнозначные логики) или |M|=D (это т.н. логики);
  
• 
  вероятностной, если истинностные значения М представляются вероятностями; степенями правдоподобия высказываний);
  
• 
  темпоральной(временной), если элементы М зависят от времени;
  
• 
  модальной, если алфавит ее языка включает связки, интерпретируемые как “возможно, что…”
  

9. 
   Формальная система – уточнение понятия аксиоматической теории, характеризующееся представлением последней в виде исчисления.
   
10. 
    Исчисление – дедуктивная система, т.е. способ задания того или иного множества путем указанных аксиом и правил вывода, каждое из которых описывает, как строить новые элементы из исходных и уже построенных.
    
11. 
    Функциональная система – множество функций с некоторым набором операций, применяемых к этим функциям и приводящих к получению других функций из этого множества.
    

КОНЦЕПТУАЛЬНЫЙ БАЗИС МАТЕМАТИЧЕСКОЙ ЛОГИКИ.
С синтаксической точки зрения в математической логике различают символы переменных, термов и формул, а с семантической точки зрения – высказываний, терминов, предикатов и логических операторов. Поясним эти символы с помощью дерева:


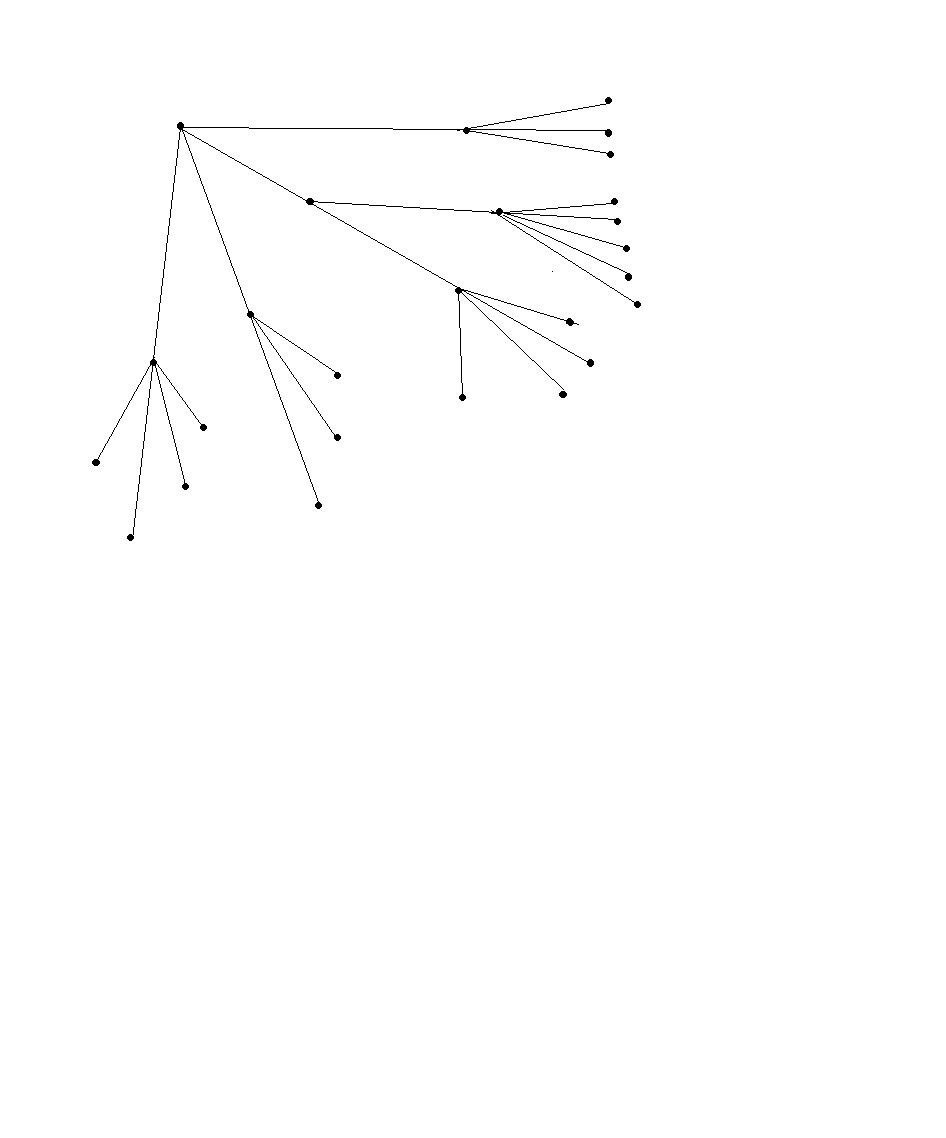
Основные понятия математической логики

высказывания

Простые высказывания

Сложные высказывания

метавысказывания

термы

Логические переменные

Предметные переменные

Пропозициональные переменные

Лингвистические переменные

Предикатные переменные

Метапеременные

Субъекты

Логические операторы

Истинностные значения

метатермbys

Логические функции

Однородные логические функции

Неоднородные логические функции (предикаты)

Метафункции

Логические формулы

Предикатные формулы

Пропозициональные формулы

метаформулы


Здесь:
А. Высказывание – абстракция осмысленного повествовательного предложения естественного языка, для которого имеет смысл говорить о его истинности или ложности (это пояснение, а не определение, понятие “высказывание” в классической логике).

• 
  Простые высказывания.
  

Примеры:

1. 
   Вычислительная система есть программно-аппаратный комплекс.
   
2. 
   57=35
   

Эти два предложения являются простыми (атомарными, элементарными) истинными высказываниями.

Примеры:

3. 
   3
   
4. 
   Волк есть дикая кошка.
   

Эти два простых высказывания являются ложными.

5) Денис скоро будет космонафтом.(не высказывание,т.к. будущее время)

Предостережения:

• 
  предложение “Всякий вечный двигатель работает без бензина ” и “ Земля вращается быстро ” не являются истинными, но в тоже время не являются и ложными. Поэтому эти предложения не являются высказываниями (очевидно, что первое предложение является бессмысленным, а второе – неопределенно-истинно);
  
• 
  предложение Х+7=9 не является высказыванием, а есть высказывательная форма (при указании конкретного значения Х имеем высказывание).
  

Следует отметить, что всякое простое,бескванторное, категоричное высказывание имеет субъектно-предикатную структуру (т.е. логическую форму, способ содержательных частей) вида a  P ( или сокращенно P_(a)), где a – субъект (субъект указывает на тот объект, о котором идет речь в высказывании);

P – предикатный терм (предикатный терм, иначе, логическое сказуемое, указывает на свойство субъекта);

 - оператор предикации;

• 
  Сложные высказывания.
  

Примеры:

1. 
   Волга – самая короткая река России и в ней живут киты;
   
2. 
   3+7=9 аналогично 7+3=2
   

Эти два высказывания, каждое из которых составлено из двух простых ложных высказываний, являются сложными (составными, молекулярными) ложными высказываниями. Очевидно, что логические формы этих высказываний следующие:

P_1(a) P_2(a) или (a  P₁)  (a  P₂),
P_3(b) P_4(b) или (b  P₃) (b P₄),

Где: a, b – субъекты (соответственно: Волга и сумма чисел);

P_1, P_2, P_3, P₄ - предикатные символы (соответственно: самая короткая река; река, в которой живут киты; равно 9; равно 2);

 - логические связки (обозначающие соответственно “и” и “аналогично”),позволяющие строить из простых высказываний сложные.

• 
  Метавысказывания – это высказывание, субъект которого указывает на другое высказывание.
  

Пример. Пусть имеем высказывание P_(a) , тогда высказывание “ P_(a) - ложно ” о высказывании P_(a) есть метавысказывание. Очевидно, на основе высказывания P_(a) можно построить неограниченное количество метавысказываний различной степени сложности. Так, например, метевысказыванием будет “высказывание “ P_(a) - ложно” - истинно”. Поскольку в математической логике сложное высказывания представляют замкнутой формулой, то высказывание о ее доказуемости (недоказуемости, выполнимости) является метавысказыванием. При этом в целях упрощения записи метавысказываний используются оператор логического

следования и оператор дедуктивной выводимости. Так, метевысказывание

___

“формула” P_(a) P_(a)” – тавтология” записывается символически |= (P_(a) P_(a)), а метавысказывание “ формула“ P_(a) P_(a) ” – логически доказуема” записывается так |(P_(a) P_(a)).