Ответы Физика первый курс. Материальная точка
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
Период пружинного маятника — зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается17. Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна 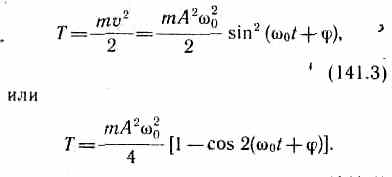 Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна 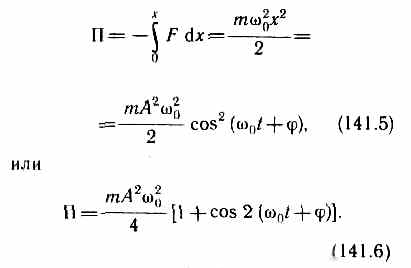 Сложив (141.3) и (141.5), получим формулу для полной энергии: 18. Математический маятник. Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести. Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; Решение этого уравнения 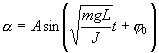 Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. Из этого соотношения определяем Период математического маятника — период колебания математического маятника зависит от длины нити: с уменьшением длины нити период колебания уменьшается19. Дифференциальное уравнение малых колебаний физического маятника (при φ≈sin φ) Кинематическое уравнение малых колебаний физического маятника где φ0 и ω0 - начальный угол отклонения от вертикали и начальная угловая скорость маятника; При амплитуде а≤8° погрешность при рассмотрении колебаний физического маятника как малых составляет менее 0,1%, при амплитуде а≤22° погрешность менее 1%. Период малых колебаний физического маятника: 20. Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Дифференциальное уравнение свободных затухающих колебаний линейной системы где s — колеблющаяся величина, описывающая тот или иной физический процесс, δ = const — коэффициент затухания, (ω0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде После нахождения первой и второй производных и их подстановки в (1) получим Решение уравнения зависит от знака коэффициента перед искомой величиной. Пусть этот коэффициент положителен: Тогда получим уравнение решением которого является функция u=A0cos(ωt+φ). Значит, решение уравнения (7.1) в случае малых затуханий График зависимости смещения от времени для затухающих колебаний выглядит следующим образом: Амплитуда убывает тем быстрее, чем больше сопротивление 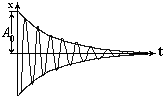 21. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ - колебания, происходящие под действием внешней переменной силы (вынуждающей силы). Для нахождения уравнения установившихся колебаний необходимо найти решение дифференциального уравнения: Общее решение этого неоднородного дифференциального уравнения представляет собой, как известно из теории дифференциальных уравнений, сумму общего решения однородного уравнения и любого частного решения неоднородного. Общее решение однородного уравнения нам известно, это - уравнение затухающих колебаний. Оно нас не интересует, так как при где А - амплитуда вынужденных колебаний, j۪ - сдвиг фаз между смещением и приложенной силой. 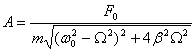 здесь w0 - частота свободных (незатухающих) колебаний маятника; b - коэффициент затухания. Обратите внимание, что амплитуда вынужденных колебаний зависит от соотношения частоты вынуждающей силы и собственной частоты маятника. Максимальное значение амплитуды получается, если Частота Механическим Резонансом (Р) называется явление возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе при приближении частоты периодического внешнего воздействия к одной из частот собственных колебаний системы. 22. При наложении двух гармонических колебаний, происходящих в одном направлении с одинаковой частотой, возникает гармоническое колебание с той же частотой, а его амплитуда зависит от амплитуд и начальных фаз отдельных колебаний. Результирующее отклонение в каждый момент времени равно алгебраической сумме составляющих отклонений. то
Многократного применения теорему сложения, получаем
при этом
и
В частном случае равных амплитуд (Ym1 = Ym2) выражения (3) и (4) упрощаются:
и
Для разности начальных фаз ∆φ = 0 или π получаем следующие частные случаи:
Обратите внимание:
23. Механические волны – процесс распространения механических колебаний в среде (жидкой, твердой, газообразной). Механические волны бывают разных видов. Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне. Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне или звуковые волны в газе являются примерами таких волн. Запишем уравнение колебания: Рассмотрим распространение волны от точки М до точки В. Из рисунка видно, что время Перейдем от уравнения колебаний к уравнению плоской бегущей волны: Т.к. за время Будем считать начальную фазу Тогда согласно уравнению (6), получаем: Если в уравнении (14)
24.. Это уравнение называетсяуравнением состояния идеального газа. Газовая постоянная (R) – одна из основных физических постоянных, входит в уравнение состояния 1 моля идеального газа R = pV/T = 1.01•105•22.4•10-3/273[Па•м3/моль]/K =8.31(44) Dж/(моль•K) 25. Идеальный газ - модель газа, в которой: - между молекулами отсутствуют силы взаимного притяжения; - сами молекулы принимаются за материальные точки; а - взаимодействия между молекулами сводится к их абсолютно упругим ударам. 26. Изопроцессы — равновесные процессы, в которых один из основных параметров сохраняется. ИЗОБАРНЫЙ ПРОЦЕСС ( Для изобарного процесса в идеальном газе справедлив закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его термодинамической температуре: 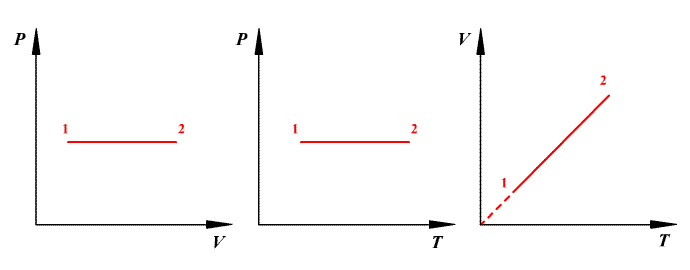 Работа газа при изобарном расширении: Изменение внутренней энергии: Количество полученного тепла в соответствии с первым началом термодинамики: Молярная теплоемкость при изобарном процессе: ИЗОХОРНЫЙ ПРОЦЕСС ( Изохорный процесс в идеальном газе описывается законом Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его термодинамической температуре: 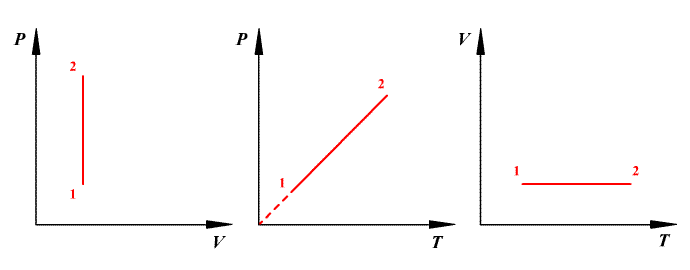 Работа газа при изохорном процессе равна нулю: Все полученное тепло идет на изменение внутренней энергии в соответствии с первым началом термодинамики: Молярная теплоемкость при изохорном процессе: ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС ( Изотермический процесс в идеальном газе подчиняется закону Бойля - Мариотта: для данной массы газа при неизменной температуре произведение значений давления и объема есть величина постоянная:  Работа газа при изотермическом расширении: 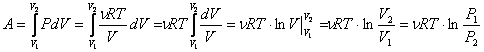 . .Изменение внутренней энергии при изотермическом процессе равно нулю: Все полученное тепло идет на совершение работы в соответствии с первым началом термодинамики: 27. Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dNмолекул однородного (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуреТ скорости, заключенные в интервале от v до v + dv. Для вывода функции распределения молекул по скоростям f(v) равной отношению числа молекул dN, скорости которых лежат в интервале v ÷v + dv к общему числу молекул N и величине интервала dv 
Условие нормировки для функции распределения имеет вид 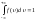 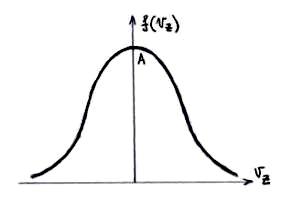 28. 28. 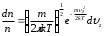 – распределение Максвелла для проекции скорости, которое определяет долю хаотически движущихся молекул идеального газа, которые имеют проекцию скорости на ось 0Z в пределах от υz до υz+dυz. – распределение Максвелла для проекции скорости, которое определяет долю хаотически движущихся молекул идеального газа, которые имеют проекцию скорости на ось 0Z в пределах от υz до υz+dυz.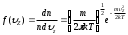 – функция распределения Максвелла для проекции скорости. – функция распределения Максвелла для проекции скорости.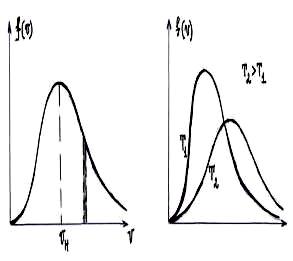 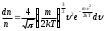 – распределение Максвелла для модуля скорости, которое определяет долю хаотически движущихся молекул идеального газа, которые имеют модуль скорости в пределах от υ до υ+dυ. – распределение Максвелла для модуля скорости, которое определяет долю хаотически движущихся молекул идеального газа, которые имеют модуль скорости в пределах от υ до υ+dυ.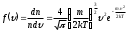 – функция распределения Максвелла для модуля скорости. – функция распределения Максвелла для модуля скорости.При увеличении температуры T максимум кривой распределения сместится вправо, так как при увеличении T увеличивается vв, которая определяет положение максимума. Но площадь под кривой должна оставаться постоянной. Поэтому величина максимума будет уменьшаться. Влияние же массы молекулы m0 будет обратным. Влияние температуры и массы молекулы на вид функции распределения показано на рис. 6. 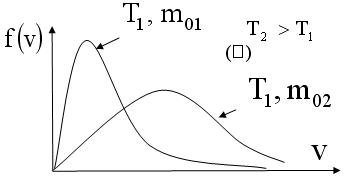  29. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА - определяет зависимость от высоты h плотности n или давления p идеального изотермического газа, находящегося в гидростатическом равновесии в однородном поле силы тяжести. Высота h отсчитывается в направлении, противоположном ускорению силы тяжести g. Для плотности Б. ф. можно записать в виде:
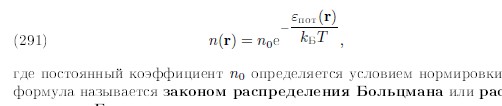 30. Сте́пени свобо́ды — характеристики движения механической системы. Числом степеней свободы материального объекта называют число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета. Каждое независимое движение называется степенью свободы. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные), а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные). При достаточно высоких температурах в многоатомных молекулах возбуждаются дополнительные – колебательные степени свободы, связанные с изменением расстояний между атомами. Например, в двухатомной молекуле при данных условиях насчитывается 6 стпеней свободы (3 поступательные, 2 вращательные и 1 колебательная). на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы. 31.Диффузия – это процесс, при котором происходит взаимное проникновение молекул одного вещества, между молекулами другого вещества, которое приводит к самопроизвольному выравниванию концентраций этих веществ по всему объему. Обычно под диффузией понимают процессы, сопровождающиеся переносом материи, однако иногда диффузионными называют также другие процессы переноса: теплопроводность, вязкое трение и т. п. Градиент плотности grad r – это вектор, который характеризует быстроту изменения скалярной величины — плотности в пространстве и направлен в сторону наиболее быстрого возрастания данной плотности. Коэффициент диффузии – количественная характеристика скорости диффузии, равная количеству вещества (в массовых единицах), проходящего в единицу времени через участок единичной площади (например, 1м²) при градиенте концентрации, равном единице (соответствующем изменению 1 моль/л → 0 моль/л на единицу длины) Фика закон диффузии —кинетическое уравнение для скорости диффузии под действием градиента концентрации. Записывается в двух формах. Г1ер-вый закон Фика оперирует с постоянным градиентом концентрации и описывает диффузионный поток вещества через единицу поверхности, а второй закон Фика относится к полям концентрации и непрерывно изменяющимсяградиентам концентрации . Он характеризует диффузионное накопление вещества в окрестностях каждой точки поля концентраций. 32. Внутреннее трениеВязкость - свойство жидкостей и газов оказывать сопротивление перемещению одной их части относительно другой. Вязкость объясняется возникновением при движении внутреннего трения между частицами. Силы внутреннего трения направлены вдоль поверхности соприкасающихся слоев и зависят от их относительных скоростей.Количественно величина различий в скорости движения слоев жидкости характеризуется градиентом скорости dv/dx, называемым также скоростью сдвига.
Это закон внутреннего вязкого трения Ньютона, который установил его экспериментально. Закон утверждает: при стационарном (ламинарном) движении слоев жидкости или газа с различными скоростями между ними возникают касательные силы, пропорциональные градиенту скорости слоев и площади их соприкосновения. Физический смысл коэффициента вязкости Согласно второму закону Ньютона,
КОЭФФИЦИЕНТ ВНУТРЕННЕГО ТРЕНИЯ — угловой коэф., выражающий зависимость сопротивления сдвигу п. от нормального давления. Условносчитается показателем сил трения между частицами п. Для песчаных п. изменяется в пределах 0,25 — 0,60,для глинистых — 0,15 — 0,35. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

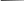 φ01−φ02
φ01−φ02 φ01+φ02
φ01+φ02