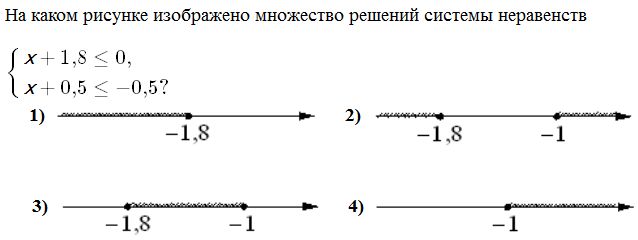
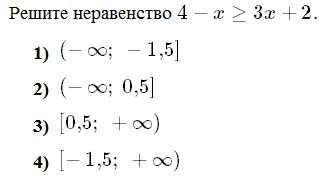Сборник ГВЭ по математике 2022. Материалы для подготовки к государственному выпускному экзамену по математике для обучающихся по образовательным программам

• Название: Материалы для подготовки к государственному выпускному экзамену по математике для обучающихся по образовательным программам
• Дата: 09.04.2022
• Размер: 1.92 Mb.
• Имя файла: Сборник ГВЭ по математике 2022.doc
• Тип: Материалы для подготовки; #457733
• страница: 2 из 4

6. 
   Н 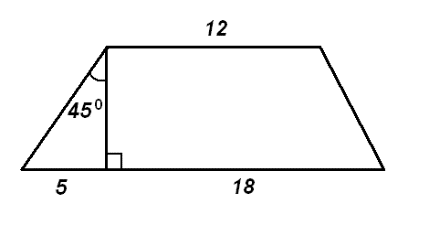айдите площадь трапеции, изображённой на рисунке.
   

3. 
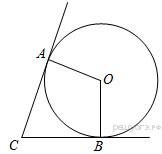   В угол C ве­ли­чи­ной 83° впи­са­на окружность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B. Най­ди­те угол AOB. Ответ дайте в градусах.
   
4. 
   Какие из следующих утверждений верны?
   

1) В параллелограмме есть два равных угла.

2) Любая биссектриса равнобедренного треугольника является его медианой.

3) Площадь прямоугольного треугольника равна произведению длин его катетов.

В ответ запишите номер выбранного утверждения.
Ответ: ___________________________.

3. 
   Семья из трёх человек едет из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно на своей машине. Билет на поезд на одного человека стоит 830 рублей. Автомобиль расходует 10 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина 19 руб. за литр. Какая поездка (поездом или машиной) обойдётся дешевле? В ответ напишите, сколько рублей она будет стоить.
   
4. 
   В закрытую коробку помещены 20 шаров: 8 из них – белые, 5 – чёрные, остальные – красные. Какова вероятность того, что, вытаскивая шары из коробки вслепую, первым мы извлечём из неё красный шар?
   

Часть 2

3. 
   Два велосипедиста одновременно отправляются в 140-километровый пробег. Первый едет со скоростью на 14 км/ч большей, чем второй, и прибывает к финишу на 5 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
   
4. 
   В выпуклом четырёхугольнике ABCD углы CDB и CAB равны. Докажите, что углы BCA и BDA также равны.
   

Вариант 5
Часть 1

1. 
   Найдите значение выражения:  
   
2. 
   Решите уравнение: .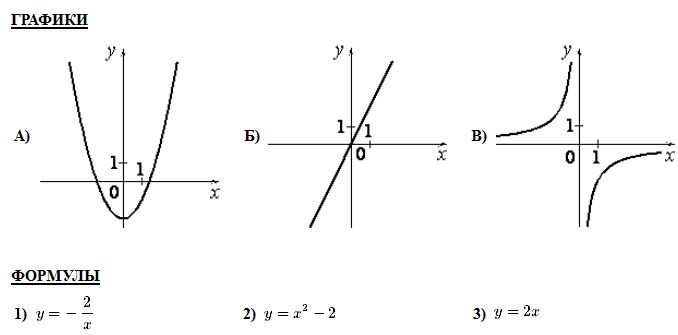
   
3. 
   Найдите значение выражения: при х= 6, у = 10
   
4. 
   
   

Сумма двух углов равнобедренной трапеции равна 178º. Найдите больший угол трапеции. Ответ дайте в градусах. Ответ: ___________________________ Точка O – центр окружности, на ко­то­рой лежат точки A, B и C. Известно, что ∠ABC = 15° и ∠OAB = 8°. Най­ди­те угол BCO. Ответ дайте в градусах. Какое из следующих утверждений верно? Площадь ромба равна произведению двух его смежных сторон на синус угла между ними. 2) Любая биссектриса равнобедренного треугольника является его медианой. 3) Сумма углов любого треугольника равна 360 градусам. Семья из трёх человек едет из Москвы в Чебоксары. Можно ехать поездом, а можно на своей машине. Билет на поезд на одного человека стоит 740 рублей. Автомобиль расходует 9 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина 19 руб. за литр. Какая поездка (поездом или машиной) обойдётся дешевле? В ответ напишите, сколько рублей она будет стоить. В закрытую коробку помещены 25 шаров: 10 из них – белые, 6 – чёрные, остальные – красные. Какова вероятность того, что, вытаскивая шары из коробки вслепую, первым мы извлечём из неё красный шар? Часть 2. Моторная лодка прошла против течения реки 210 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч. В выпуклом четырёхугольнике ABCD углы CDB и CAB равны. Докажите, что углы BCA и BDA также равны.

 

Вариант 6

Часть1

1. 
   Найдите значение выражения: 5,3 – 9∙(-4,4) =
   

Ответ: ___________________________.

2. 
   Решите уравнение (−4x − 2)(4x − 1) = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
   

Ответ: ___________________________.

3. 
   Найдите значение выражения : при а = -0,5
   
4. 
   Установите соответствие между графиками функций и формулами, которые их задают.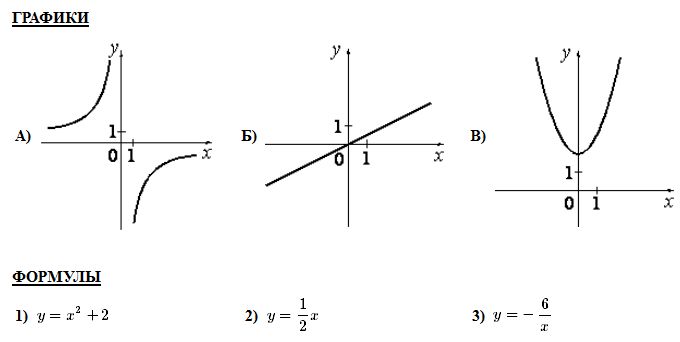 
   
   
5. 
   Найдите наибольшее значение x, удовлетворяющее системе неравенств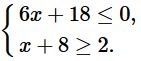 
   
   

Ответ____________

6. 
   Катеты прямоугольного треугольника равны 18 и 24. Найдите гипотенузу этого треугольника.
   

Ответ: ___________________________.

7.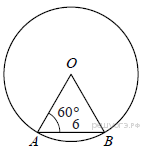 
   Ц ен­траль­ный угол AOB опи­ра­ет­ся на хорду AB дли­ной 6. При этом угол OAB равен 60°. Най­ди­те радиус окружности.
   

8. 
   Какое из следующих утверждений верно?
   

1) Средняя линия трапеции равна полусумме её оснований.

2) Диагонали любого прямоугольника делят его на 4 равных треугольника.

3) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
9. Принтер печатает одну страницу за 6 секунд. Сколько страниц можно
напечатать на этом принтере за 9 минут?

Ответ:___________________________.
10.Родительский комитет закупил 25 пазлов для подарков детям в связи
с окончанием учебного года, из них 18 с машинами и 7 с видами городов.
Подарки распределяются случайным образом между 25 детьми, среди
которых есть Володя. Найдите вероятность того, что Володе достанется пазл
с машиной.

Ответ: ___________________________.
Часть 2

11. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
12. Основания ВС и AD трапеции АВСD равны соответственно 5 и 45, BD = 15. Докажите, что треугольники CBD и BDA подобны.

Вариант 7
Часть1

1. 
   Найдите значение выражения: 6,3 – 4∙(-2,3) =
   

Ответ: ___________________________.

2. 
   Решите уравнение (4x − 3)(−2x − 8) = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
   

Ответ: ___________________________.

3. 
   Найдите значение выражения : при а = -79; b = -2.
   

4. 
   Установите соответствие между графиками функций и формулами, которые их задают.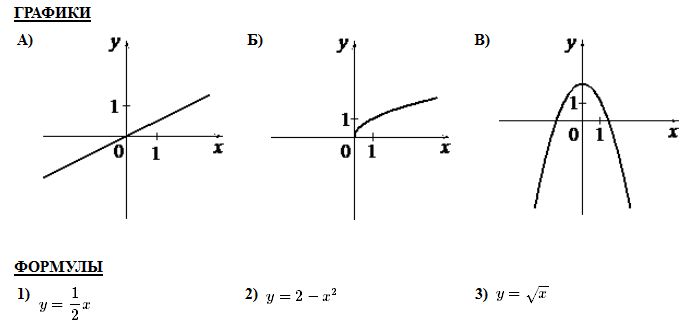 
   
   

5. 
   Найдите наименьшее значение x, удовлетворяющее системе неравенств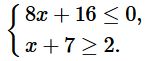 
   
   

Ответ ________________________.

6. 
   Периметр квадрата равен 84. Найдите площадь этого квадрата.
   Ответ:___________.
   
7.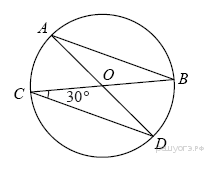 
   В окруж­но­сти с цен­тром в точке О про­ве­де­ны диаметры AD и BC, угол OCD равен 30°. Най­ди­те величину угла OAB.
   

8. Какие из следующих утверждений верны?

1) Существуют три прямые, которые проходят через одну точку.

2) У любой трапеции боковые стороны равны.

3) Сумма углов равнобедренного треугольника равна 180 градусам.
9. Площадь земель крестьянского хозяйства, отведённая под посадку
сельскохозяйственных культур, составляет 49 гектаров и распределена между
зерновыми культурами и картофелем в отношении 2 : 5 . Сколько гектаров
занимает картофель?

Ответ:________________________.

10. 
    Вероятность того, что новая шариковая ручка пишет плохо (или не пишет),равна 0,26. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
    

Ответ: ___________________________.
Часть 2

10. 
    Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
    

10. 
    Биссектрисы углов А и В трапеции АВСD с основаниями AD и ВС пересекаются в точке К. Докажите, что точка К равноудалена от прямых АВ, ВС и AD.
    
    
    

Вариант 8
Часть1

1. Найдите значение выражения 0,7( - 10)³ - 20 =

Ответ: ___________________________.
2.Решите уравнение (6x − 6)(3x + 3) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ___________________________.

2. 
   Найдите значение выражения : при х= 1, у = 7
   

2. 
   Установите соответствие между графиками функций и формулами, которые их задают.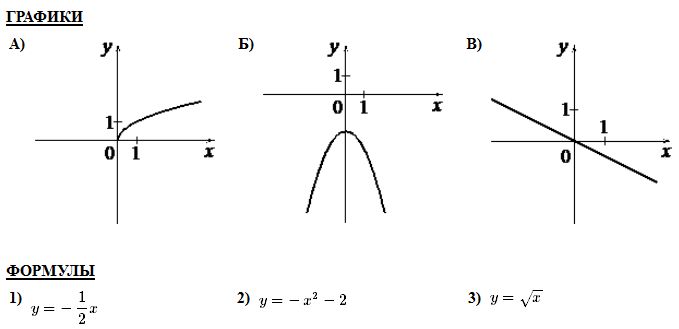 
   
   

2. 
   В трапеции средняя линия равна 12, меньшее основание 5. Найдите длину большего основания.
   

Ответ_______________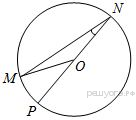

2. 
   Найдите гра­дус­ную меру ∠MON, если известно, NP — диаметр, а гра­дус­ная мера ∠MNP равна 18°.
   

2. 
   Какое из следующих утверждений верно?
   

1) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.

2) Любая биссектриса равнобедренного треугольника является его медианой.

3) Сумма углов любого треугольника равна 360 градусам.

2. 
   Спортивный магазин проводит акцию. Любая футболка стоит 200 рублей.
   При покупке двух футболок — скидка на вторую футболку 80%. Сколько
   рублей придётся заплатить за покупку двух футболок в период действия
   акции?
   

Ответ;________________________.

2. 
   На экзамене 40 билетов, Оскар не выучил 12 из них. Найдите вероятность того, что ему попадётся выученный билет.
   

Ответ: ___________________________.
Часть2

2. 
   На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
   

12. В выпуклом четырёхугольнике ABCD углы CDB и CAB равны. Докажите,
что углы BCA и BDA также равны.


Вариант 9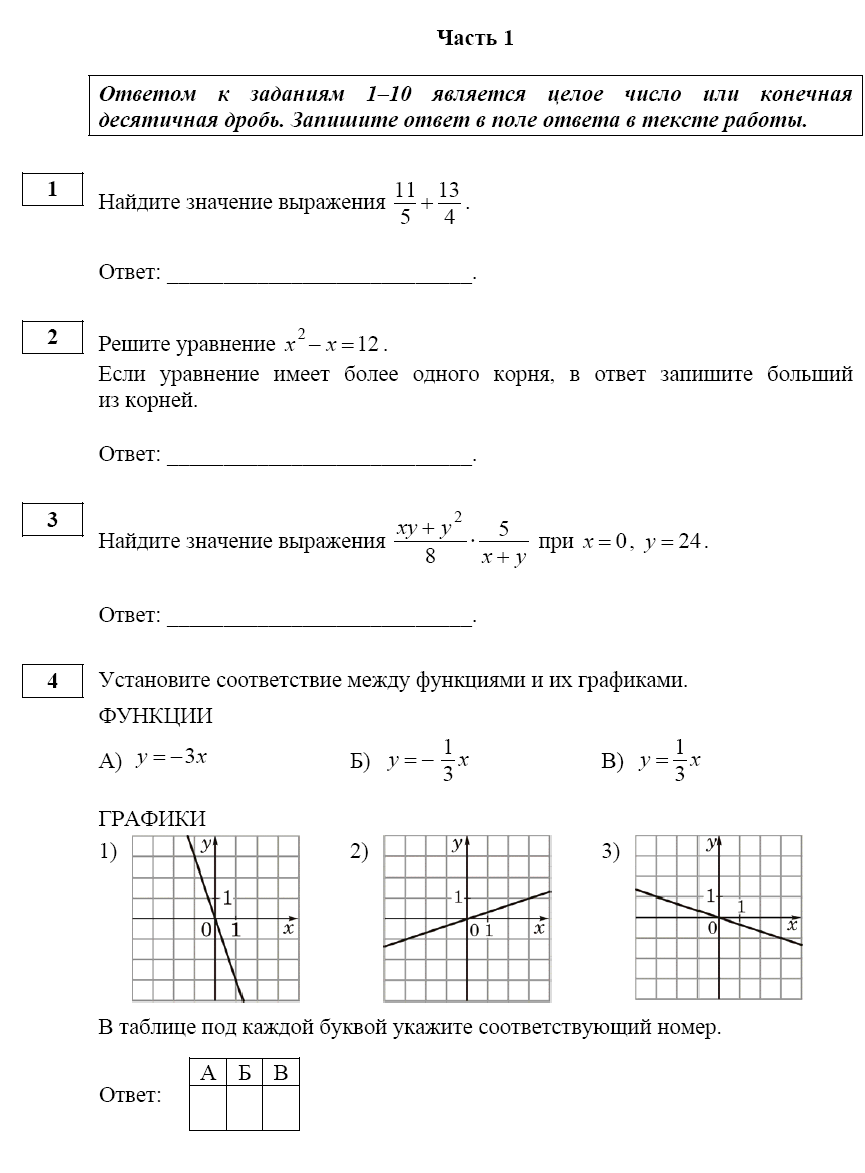







Вариант 10.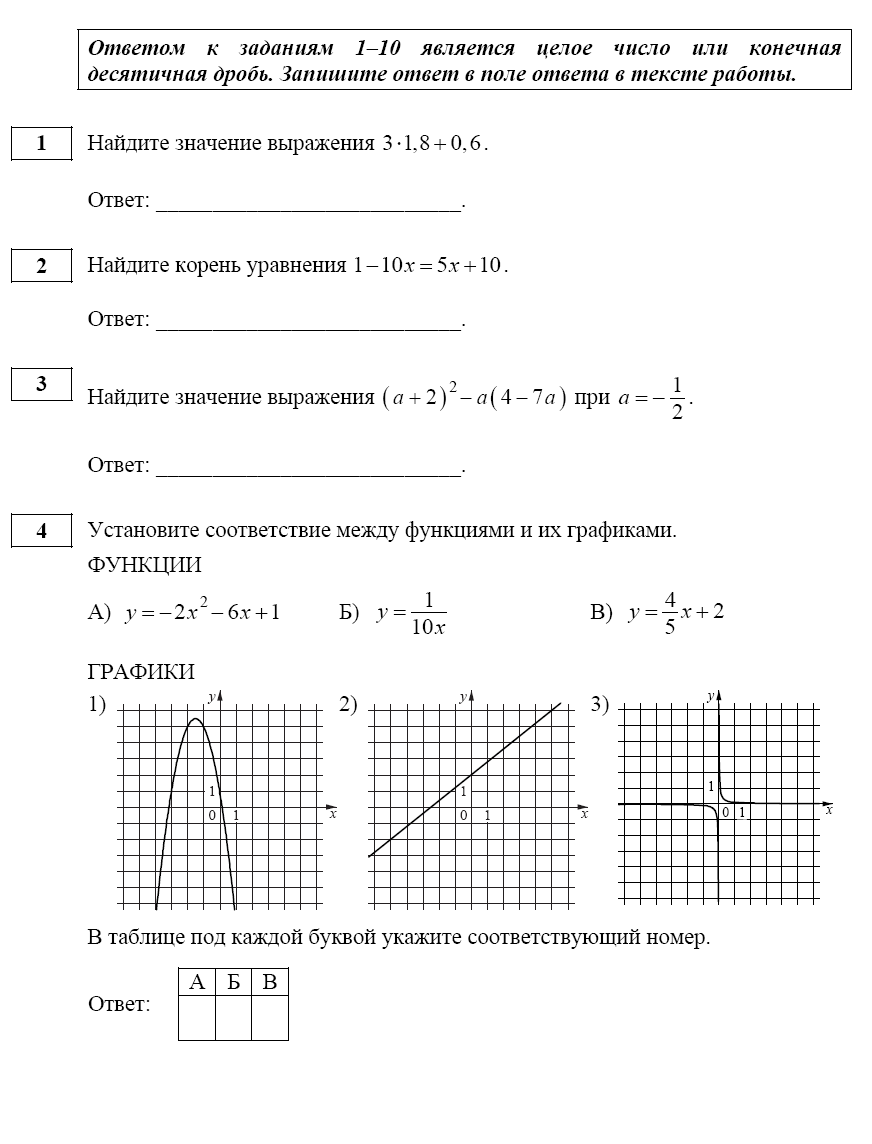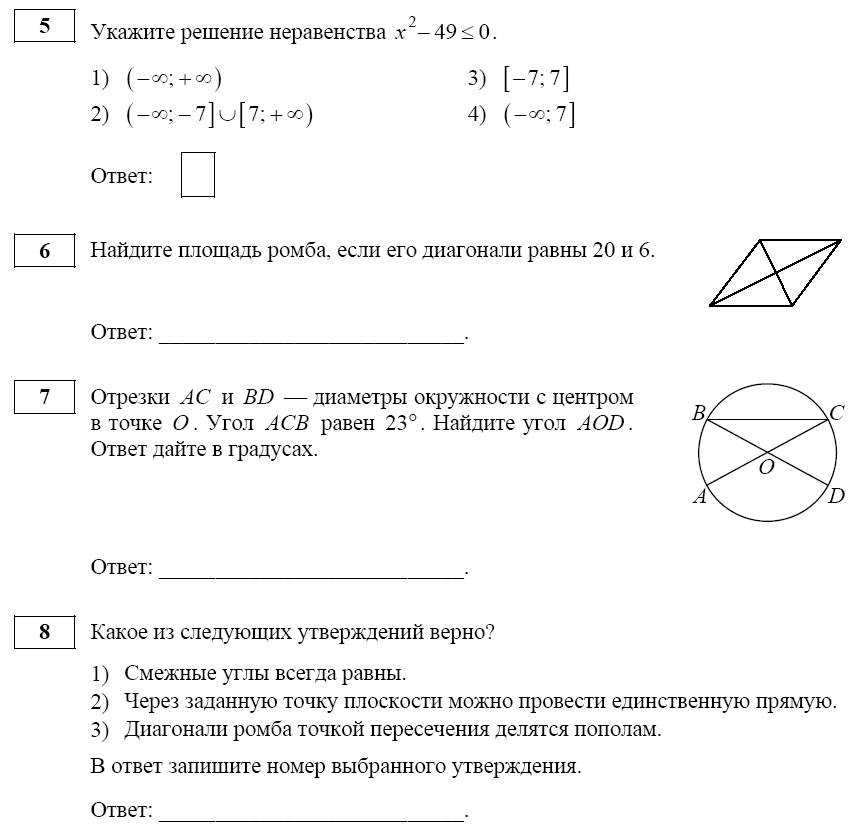




Часть 2

11. Теплоход проходит по течению реки до пункта назначения 165 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 18 часов после отплытия из него.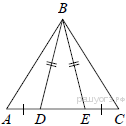

2. 
   Н а стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
   

Вариант 11.

Часть 1

1. 
   Найдите значение выражения:  
   

Ответ________________________

2. 
   Найдите корни урав­не­ния  .
   

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Ответ________________________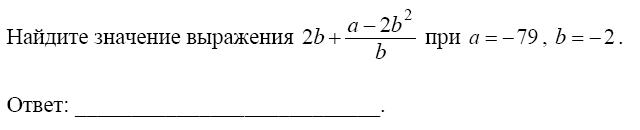

3. 
   
   

4. 
   Установите со­от­вет­ствие между гра­фи­ка­ми функ­ций и формулами, ко­то­рые их задают.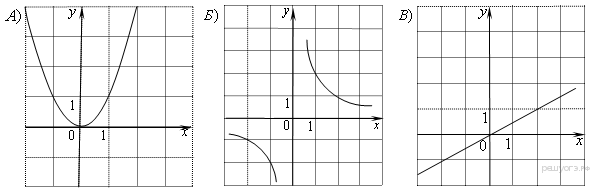
   

 

1) 

2) 

3) 

4) 

 

Ответ ука­жи­те в виде по­сле­до­ва­тель­но­сти цифр без про­бе­лов и за­пя­тых в ука­зан­ном порядке.

 

А	Б	В

 

5. 
   
   

6. 
   
   

7. 
   
   

 

8. 
   
   

9. 
   
   

Ответ___________________

10. 
    
    

Часть 2.

11. 
    Теплоход проходит по течению реки до пункта назначения 285 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 34 км/ч, стоянка длится 19 часов, а в пункт отправления теплоход возвращается через 36 часов после отплытия из него.
    

12. 
    В остроугольном треугольнике ABC точки A, C, центр описанной окружности O и центр вписанной окружности L лежат на одной окружности. Докажите, что угол ABC равен 60°
    

Вариант 12.

Часть 1

1. 
   Найдите значение выражения:  
   

Ответ________________________

2. 
   Решите урав­не­ние  .
   

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Ответ________________________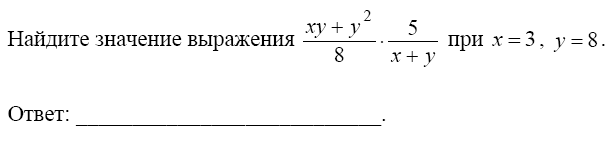

3. 
   
   

4. 
   На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = kx + b. Уста­но­ви­те со­от­вет­ствие между зна­ка­ми ко­эф­фи­ци­ен­тов k и b и гра­фи­ка­ми функ­ций.
   

 

Графики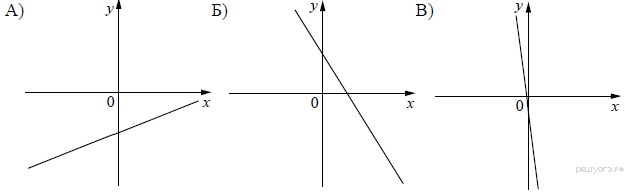

 



 

Коэффициенты

 

1) k > 0, b < 0

2) k < 0, b < 0

3) k < 0, b > 0

4) k > 0, b > 0

 

Запишите в ответ цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам: 

А	Б	В
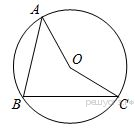
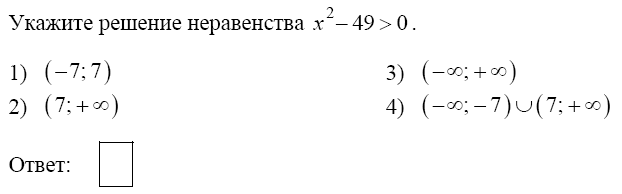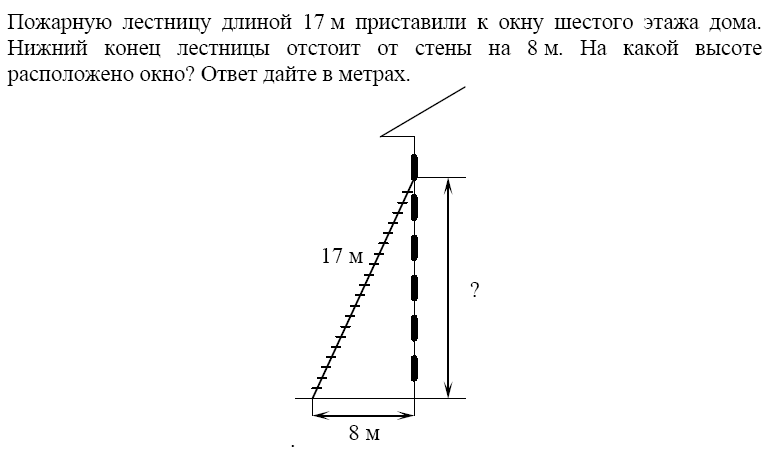Ответ_________________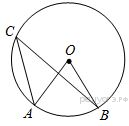

5. 
   
   

6. 
   
   

Ответ____________________

7. 
   Точка О — центр окруж­но­сти, ∠AOB = 84° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла ACB (в гра­ду­сах).
   

Ответ______________

8. 
   
   

9. 
   
   

Ответ________________

10. 
    
    

Часть 2.

11. 
    Пер­вый ве­ло­си­пе­дист вы­ехал из посёлка по шоссе со ско­ро­стью 18 км/ч. Через час после него со ско­ро­стью 16 км/чиз того же посёлка в том же на­прав­ле­нии вы­ехал вто­рой ве­ло­си­пе­дист, а ещё через час — тре­тий. Най­ди­те ско­рость тре­тье­го ве­ло­си­пе­ди­ста, если сна­ча­ла он до­гнал вто­ро­го, а через 4 часа после этого до­гнал пер­во­го.
    
12. 
    В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм — прямоугольник.
    

Вариант 13

1. 
   Най­ди­те зна­че­ние вы­ра­же­ния .
   

2. 
   При каком значении x значения выражений 3x−2 и 2x+6 равны?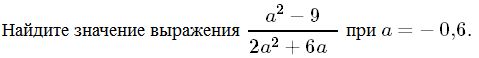
   

3. 
   
   

4. Установите соответствие между графиками и формулами, которые их задают.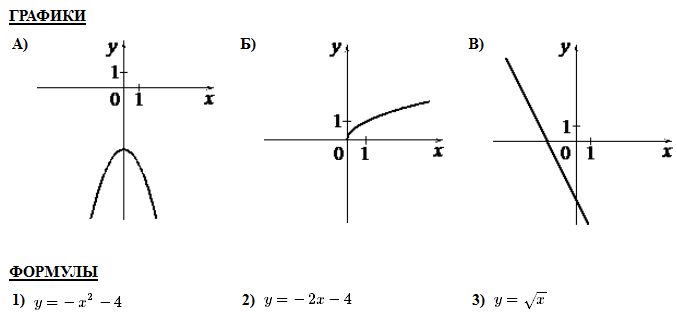


5. На каком рисунке изображено множество решений неравенства 

6. 
   Сумма двух углов равнобедренной трапеции равна 222°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
   

7. Найдите площадь трапеции, изображённой на рисунке.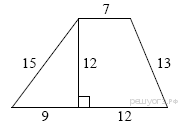


8. Укажите номера верных утверждений.
1)В треугольнике против меньшего угла лежит меньшая сторона.

2) В треугольнике против меньшей стороны лежит больший угол.

3)В треугольнике против меньшей стороны лежит меньший угол.

4) В треугольнике ABC, для которого А=400, В=600, С=800, сторона AC наибольшая.
9. Городской бюджет составляет 59 млн рублей, а расходы на одну из его статей составили 35%. Сколько рублей потрачено на эту статью бюджета?
10. На экзамене 60 билетов, Стас не выучил 6 из них. Найдите вероятность того, что ему попадётся выученный билет.
Часть2.
11. Из пунк­та А в пункт В, рас­сто­я­ние между ко­то­ры­ми 13 км, вышел пе­ше­ход. Од­но­вре­мен­но с ним из В в А вы­ехал ве­ло­си­пе­дист. Ве­ло­си­пе­дист ехал со ско­ро­стью, на 11 км/ч боль­шей ско­ро­сти пе­ше­хо­да, и сде­лал в пути по­лу­ча­со­вую оста­нов­ку. Най­ди­те ско­рость пе­ше­хо­да, если из­вест­но, что они встре­ти­лись в 8 км от пунк­та В.
12. На сто­ро­не АС тре­уголь­ни­ка АВС вы­бра­ны точки D и E так, что от­рез­ки AD и CE равны (см. рисунок). Оказалось, что от­рез­ки BD и BE тоже равны. Докажите, что тре­уголь­ник АВС — равнобедренный.

Вариант 14

1. 
   Найдите значение выражения  .
   

2. 
   При каком значении x значения выражений x−1 и 5x+2 равны?
   

3. 
   
   

4. 
   Установите соответствие между графиками и формулами, которые их задают.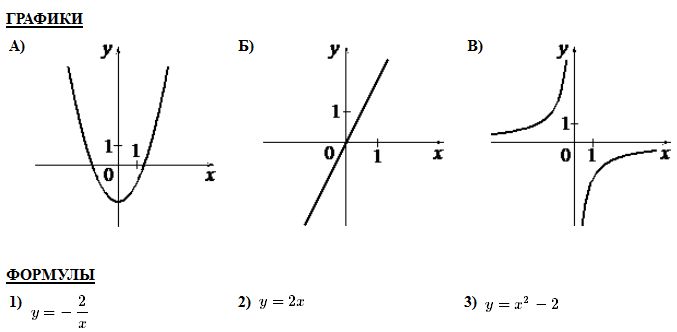
   

5. 
   На каком рисунке изображено множество решений неравенства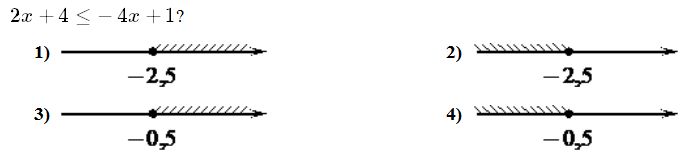 
   

6. 
   Сумма двух углов равнобедренной трапеции равна 294°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
   

7. 
   Найдите площадь трапеции, изображённой на рисунке.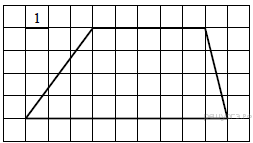
   

8. 
   Укажите номера верных утверждений.
   

1)Если две параллельные прямые пересечены третьей прямой, то внутренние односторонние углы равны.

2)Через любую точку проходит более одной прямой.

3)Любые три прямые имеют не менее одной общей точки.

4)Любые две прямые имеют не менее одной общей точки.

9. 
   Городской бюджет составляет 14 млн рублей, а расходы на одну из его статей составили 45%. Сколько рублей потрачено на эту статью бюджета?
   

10. 
    На экзамене 20 билетов, Сергей не выучил 5 из них. Найдите вероятность того, что ему попадётся выученный билет.
    

Часть 2

11. 
    Расстояние между го­ро­да­ми А и В равно 490 км. Из го­ро­да А в город В со ско­ро­стью 55 км/ч вы­ехал пер­вый автомобиль, а через час после этого нав­стре­чу ему из го­ро­да В вы­ехал со ско­ро­стью 90 км/ч вто­рой автомобиль. На каком рас­сто­я­нии от го­ро­да А ав­то­мо­би­ли встретятся?
    

12. 
    В тре­уголь­ни­ке ABC с тупым углом ACB про­ве­де­ны вы­со­ты AA₁ и BB₁. Докажите,
    

что тре­уголь­ни­ки A₁CB₁ и ACB подобны.

Вариант 15

1. 
    Найдите значение выражения 
   
2. 
   При каком значении x значения выражений 2x−4 и 3x+2 равны?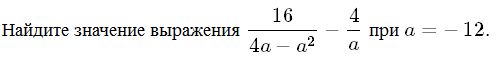
   
3. 
   
   
4. 
   Установите соответствие между графиками и формулами, которые их задают.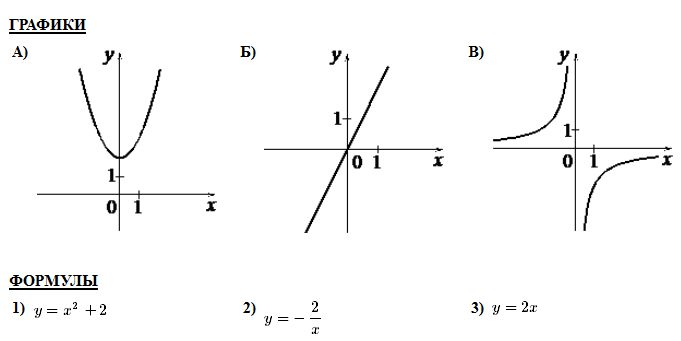
   

5. 
   На каком рисунке изображено множество решений неравенства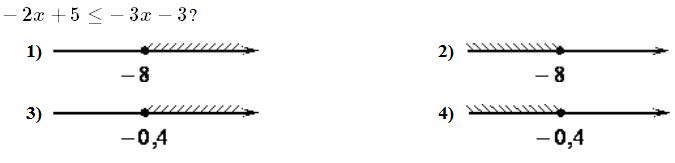 
   

6. 
   Сумма двух углов равнобедренной трапеции равна 318°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
   

7. 
   Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
   

8. 
   Укажите номера верных утверждений.
   

1. 
   Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 70°, то две прямые параллельны.
   

2) Любые три прямые имеют не менее одной общей точки.

3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

4) Сумма вертикальных углов равна 180°.

9. Городской бюджет составляет 76 млн рублей, а расходы на одну из его статей составили 20%. Сколько рублей потрачено на эту статью бюджета?

10. Из 1500 карт памяти, поступивших в продажу, в среднем 30 не работают. Какова вероятность того, что случайно выбранная карта работает?

Часть 2

11. Расстояние между го­ро­да­ми А и В равно 375 км. Город С на­хо­дит­ся между го­ро­да­ми А и В. Из го­ро­да А в город В вы­ехал автомобиль, а через 1 час 30 минут сле­дом за ним со ско­ро­стью 75 км/ч вы­ехал мотоциклист, до­гнал ав­то­мо­биль в го­ро­де С и по­вер­нул обратно. Когда он вер­нул­ся в А, ав­то­мо­биль при­был в В. Най­ди­те рас­сто­я­ние от А до С.

12. В рав­но­сто­рон­нем тре­уголь­ни­ке ABC точки M, N, K — се­ре­ди­ны сто­рон АВ, ВС, СА соответственно. Докажите, что тре­уголь­ник MNK — равносторонний.

Вариант 16

1. 
   Найдите значение выражения 
   
2. 
   При каком значении x значения выражений 3x−4 и 7x+6 равны?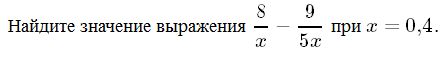
   
3. 
   
   
4. 
   Установите соответствие между графиками и формулами, которые их задают.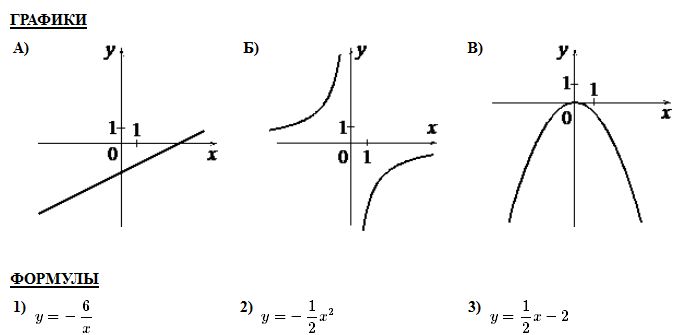
   

5. 
   На каком рисунке изображено множество решений неравенства 
   

6. 
   Диагональ прямоугольника образует угол 86° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
   

7. 
   Найдите площадь параллелограмма, изображённого на рисунке.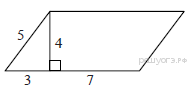
   

8. 
   Укажите номера верных утверждений.
   

1) Через любые три точки проходит не менее одной прямой.

2) Если расстояние от точки до прямой больше 1, то и длина любой наклонной, проведенной из данной точки к прямой, больше 1.

3) Любые три прямые имеют не более одной общей точки.

4) Любые две прямые имеют ровно одну общую точку.

9. 
   Для приготовления фарша взяли говядину и свинину в отношении 7:33. Какой процент в фарше составляет свинина?
   

10. 
    Из 500 мониторов, поступивших в продажу, в среднем 15 не работают. Какова вероятность того, что случайно выбранный монитор работает?
    

Часть 2

11. 
    Расстояние между го­ро­да­ми А и В равно 750 км. Из го­ро­да А в город В со ско­ро­стью 50 км/ч вы­ехал пер­вый автомобиль, а через три часа после этого нав­стре­чу ему из го­ро­да В вы­ехал со ско­ро­стью 70 км/ч вто­рой автомобиль. На каком рас­сто­я­нии от го­ро­да А ав­то­мо­би­ли встретятся?
    

12. 
    Докажите, что бис­сек­три­сы углов при ос­но­ва­нии рав­но­бед­рен­но­го тре­уголь­ни­ка равны.
    

Вариант 17

1. 
    Найдите значение выражения 
   
2. 
   Найдите корень уравнения -4х - 2 = -3х.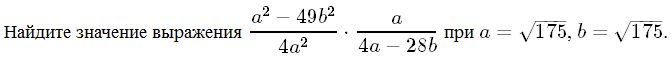
   
3. 
   
   

4. 
   Установите соответствие между графиками и формулами, которые их задают.
   

5. 
   На каком рисунке изображено множество решений неравенства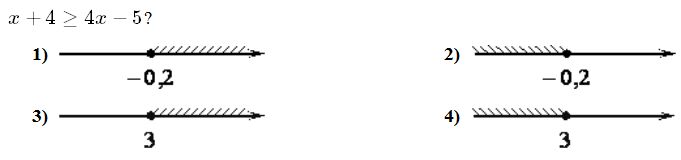 
   

6. 
   Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
   
7. 
   Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
   

8. 
   Укажите номера верных утверждений.
   

1. 
   Если угол равен 450, то вертикальный с ним угол равен 450.
   
2. 
   Любые две прямые имеют ровно одну общую точку.
   
3. 
   Через любые три точки проходит ровно одна прямая.
   
4. 
   Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
   

9. 
   Число дорожно-транспортных происшествий в летний период составило 0,59 числа ДТП в зимний период. На сколько процентов уменьшилось число дорожно-транспортных происшествий летом по сравнению с зимой?
   
10. 
    Из 600 луковиц тюльпанов в среднем 48 не прорастают. Какова вероятность того, что случайно выбранная и посаженная луковица прорастёт?
    

Часть 2

11. 
    Из пунк­та А в пункт В, рас­сто­я­ние между ко­то­ры­ми 13 км, вышел пе­ше­ход. Од­но­вре­мен­но с ним из В в А вы­ехал ве­ло­си­пе­дист. Ве­ло­си­пе­дист ехал со ско­ро­стью, на 11 км/ч боль­шей ско­ро­сти пе­ше­хо­да, и сде­лал в пути по­лу­ча­со­вую оста­нов­ку. Най­ди­те ско­рость пе­ше­хо­да, если из­вест­но, что они встре­ти­лись в 8 км от пунк­та В.
    
12. 
    Сторона AB па­рал­ле­ло­грам­ма ABCD вдвое боль­ше сто­ро­ны BC. Точка N — се­ре­ди­на сто­ро­ны AB. Докажите, что CN — бис­сек­три­са угла BCD.
    

Вариант 18

1. 
   Найдите значение выражения 
   

2. 
   Найдите корень уравнения -5х - 2 = -3х.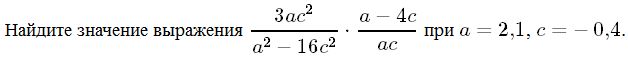
   
3. 
   
   

4. 
   Установите соответствие между графиками и формулами, которые их задают.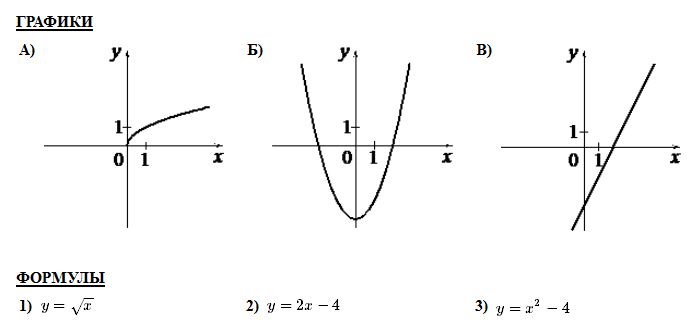
   

5. 
   На каком рисунке изображено множество решений неравенства 
   

6. 
   Диагональ прямоугольника образует угол 70° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
   

7. 
   Найдите площадь трапеции, изображённой на рисунке.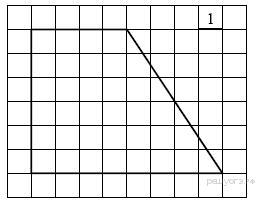
   

8. 
   Укажите номера верных утверждений.
   

1. 
   Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
   
2. 
   Любые две прямые имеют не менее одной общей точки.
   
3. 
   Через любую точку проходит более одной прямой.
   
4. 
   Любые три прямые имеют не менее одной общей точки.
   

9. 
   Число хвойных деревьев в парке относится к числу лиственных как 1:4. Сколько процентов деревьев в парке составляют лиственные?
   

10. 
    Из 1000 продающихся батареек в среднем 90 разряжены. Какова вероятность того, что случайно выбранная батарейка исправна?
    

Часть 2

11. 
    Из пунктов А и В, расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от А. Найдите скорость пешехода, шедшего из А, если известно, что он шёл со скоростью, на 1 км/ч большей, чем пешеход, шедший из В, и сделал в пути получасовую остановку
    

12. 
    Точка K — се­ре­ди­на бо­ко­вой сто­ро­ны CD тра­пе­ции ABCD. Докажите, что пло­щадь тре­уголь­ни­ка KAB равна по­ло­ви­не пло­ща­ди трапеции.
    

Вариант 19

Часть 1

1. 
   Найдите зна­че­ние вы­ра­же­ния 
   
2. 
   Найдите корень уравнения
   

Если кор­ней несколько, за­пи­ши­те их в ответ без пробелов в порядке возрастания.

3. 
   Какое из следующих выражений равно  ?
   

В ответе укажите номер правильного варианта.

 

1) 

2) 

3) 

4) 
4. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = ax² + bx + c. Для каж­до­го гра­фи­ка ука­жи­те со­от­вет­ству­ю­щее ему зна­че­ния ко­эф­фи­ци­ен­та a и дис­кри­ми­нан­та D.

 

Графики

А)

Б)

В)

Г)

Знаки чисел

 

1) a > 0, D > 0

2) a > 0, D < 0

3) a < 0, D > 0

4) a < 0, D < 0

 

Запишите в ответ цифры, рас­по­ло­жив их в порядке, со­от­вет­ству­ю­щем буквам: 
5.Най­ди­те наи­боль­шее зна­че­ние x, удо­вле­тво­ря­ю­щее си­сте­ме не­ра­венств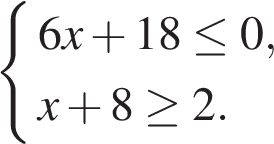

 



 

6. Пло­щадь ромба равна 27, а пе­ри­метр равен 36. Най­ди­те вы­со­ту ромба.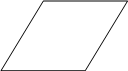

7. AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 36°. Най­ди­те угол AOD. Ответ дайте в градусах.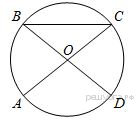