ММвХТ экзамен. Метод наименьших квадратов

• Название: Метод наименьших квадратов
• Дата: 29.11.2020
• Размер: 1.77 Mb.
• Имя файла: ММвХТ экзамен.docx
• Тип: Документы; #154939
• страница: 1 из 4

1. 
   Метод наименьших квадратов.
   

		Для упрощения изложения рассмотрим сначала случай линейной функции одного аргумента. Пусть из опыта получены точки:
x1, y1,
x2, y2, ...
xn, yn

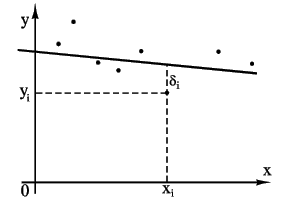
Требуется найти уравнение прямой

y=ax+b,

наилучшим образом согласующейся с опытными точками.

Пусть мы нашли такую прямую. Обозначим через расстояние опытной точки от этой прямой (измеренное параллельно оси y).

Из уравнения y=ax+b следует, что

Чем меньше числа по абсолютной величине, тем лучше подобрана прямая y=ax+b. В качестве характеристики точности подбора прямой можно принять сумму квадратов

Покажем, как можно подобрать прямую y=ax+b так, чтобы сумма квадратов S была минимальной. Из уравнений ( ) и ( ) получаем

Условия минимума S будут

Уравнения выше можно записать в таком виде:

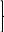- из этих уравнений легко найти a и b по опытным значениям x_i и y_i. Прямая y=ax+b, определяемая уравнениями этими , называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения, из которых определяется прямая, называются нормальными уравнениями.Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки и уравнение y=ax+b, можно записать систему уравнений для a и b

y1=ax1+b,
y2=ax2+b, ...
yn=axn+b,

Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на x₁, x₂, ..., x_n) и сложим полученные уравнения, в результате получится первое нормальное уравнение

Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение

Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции

y=a0+a1x+a2x2+...+anxn.

Естественно, что здесь получится система из n+1 нормального уравнения для определения величин
a₀, a₁, a₂, ..., a_n.
Рассмотрим частный случай применения метода наименьших квадратов. Пусть из теории известно, что

k=y/x

есть величина постоянная и ее нужно определить по опытным данным.

Систему уравнений для k можно записать

k=y1/x1,
k=y2/x2, ...
k=yn/xn,

Для получения нормального уравнения умножим каждое из этих уравнений на коэффициент при неизвестной k, т.е. на 1, и сложим полученные уравнения

отсюда

Следовательно, среднее арифметическое, полученное из опытных отношений y_i/x_i, дает решение поставленной задачи по методу наименьших квадратов. Это важное свойство средней арифметической объясняет ее широкое применение в практике обработки опытных данных.
Оценка точности метода наименьших квадратов

Дадим оценку точности метода для линейного случая, когда имеет место уравнение y=ax+b. Пусть опытные значения x_i являются точными, а опытные значения y_i имеют случайные ошибки с одинаковой дисперсией для всех i.

Введем обозначение

Тогда решения нормальных уравнений можно представить в виде

где
Из уравнения находим
Аналогично из уравнения ( ) получаем
так как
Из уравнений выше находим

Уравнения ( ) и ( ) дают оценку точности коэффициентов, определенных по нормальным уравнениям.

2. 
   Численные методы поиска минимума функции одной переменной.
   

Функция f(x) имеет локальный минимум при некотором 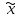, если существует некоторая конечная ξ-окрестность этого элемента, в которой 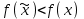, 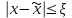. Требуется, чтобы на множестве X функция f(x) была по крайней мере кусочно-непрерывной.

Точка, в которой функция достигает наименьшего на множестве X значения, называется абсолютным минимумом функции. Для нахождения абсолютного минимума требуется найти все локальные минимумы и выбрать наименьшее значение.

Задачу называют детерминированной, если погрешностью вычисления (или экспериментального определения) функции f(x) можно пренебречь. В противном случае задачу называют стохастической. Все изложенные далее методы применимы только к детерминированным задачам.

3. 
   Численные методы поиска минимума функции нескольких переменных.
   

Будем рассматривать методы поиска минимума 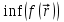в многомерных задачах на примере функции двух переменных f(x, y), так как эти методы легко аппроксимировать на случай трех и более измерений. Все эффективные методы поиска минимума сводятся к построению траекторий, вдоль которых функция убывает. Разные методы отличаются способами построения таких траекторий, так как метод, приспособленный к одному типу рельефа, может оказаться плохим для рельефа другого типа. Различают следующие типы рельефа:

4. 
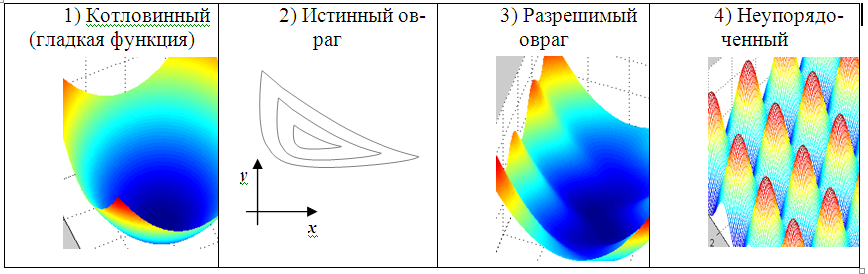   Решение уравнений графическим методом.
   

Например, для нахождения тем­пературы кипения жидкой смеси, состоящей из двух компонентов, можно воспользоваться следующим уравнением:

Р = ехр(A₁ - B₁/(t+C₁+273.15)) x₁ + ехр(A₂ – B₂/(t + C₁ + 273.15)) x₂,

где x₁- и x₂ - мольные доли компонентов в смеси.

Выразить переменную t из уравнения в явном виде сложно. Од­нако решение может быть легко получено при помощи численных методов.

В общем случае нелинейное алгебраическое уравнение можно записать в виде: F(x) = 0,

где функция F(x) определена и непрерывна на конечном или бесконечном интервале [а, b].
Любое уравнение можно преобразовать в функцию вида F(x)=0. Для этого всю правую часть уравнения (часть правее знака равенства) следует перенести влево. Принимая во внимание, что действительные корни уравнения F(x) = 0 - это точки пересечения графика функции F(x) с осью абсцисс, достаточно построить график функции F(x) и отметить точки пересечения F(x) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. К примеру, уравнение Р = ехр(A₁ - B₁/(t+C₁+273.15)) x₁ + ехр(A₂ – B₂/(t + C₁ + 273.15)) x₂, можно преобразовать в следующую функцию y(t)
y(t) = P - ехр(A₁ - B₁/(t+C₁+273.15)) x₁ - ехр(A₂ – B₂/(t + C₁ + 273.15)) x_2.
Значение переменной t, при котором функция y(t) равняется нулю, и будет температурой кипения смеси.

5. 
   Отделение корней.
   

Например, для нахождения тем­пературы кипения жидкой смеси, состоящей из двух компонентов, можно воспользоваться следующим уравнением:

Р = ехр(A₁ - B₁/(t+C₁+273.15)) x₁ + ехр(A₂ – B₂/(t + C₁ + 273.15)) x₂,

где x₁- и x₂ - мольные доли компонентов в смеси.

Выразить переменную t из уравнения в явном виде сложно. Од­нако решение может быть легко получено при помощи численных методов.

В общем случае нелинейное алгебраическое уравнение можно записать в виде: F(x) = 0,

где функция F(x) определена и непрерывна на конечном или бесконечном интервале [а, b]. Нелинейные уравнения с одним неизвестным подразделяются на алгебраические и трансцендентные. Уравнение F(x) = 0 называется алгебраическим, если функция является алгебраической функцией.

Всякое алгебраическое уравнение имеет, по крайней мере, один корень вещественный или комплексный.

Если функция F(x) не является алгебраической, то уравнение F(x) = 0 называется трансцендентным.

В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.

Поскольку подавляющее большинство нелинейных уравнений с одной переменной не решается путем аналитических преобразований (точными методами), на практике их решают только численными методами. Решить такое уравнение — это значит установить, имеет ли оно корни, сколько корней, и найти значения корней с заданной точностью. Задача численного нахождения действительных и комплексных корней уравнения F(x) = 0 обычно состоит из двух этапов: отделение корней, т. е. нахождение достаточно малых окрестностей рассматриваемой области, в которых содержится одно значение корня, и уточнение корней, т. е. вычисление корней с заданной степенью точности в некоторой окрестности. Для отделения корней могут быть использованы как графические методы решения уравнений, так и специальные алгоритмы.

6. 
   Решение уравнений аналитическими методами.
   

Решить любое уравнение y(x)=0 можно аналитически, символьно или с помощью встроенных стандартных функций. Для этого в SMath Studio предназначены следующие функции.

Функцию polyroots (возвращает корни полинома, заданного вектором его коэфициентов) можно использовать для нахождения корней полинома степени n, имеющего вид

a_nxⁿ + ... + a₂x² +a₁x + a₀.
Эта функция не требует начального приближения и возвращает сразу все n корней, как вещественные, так и комплексные.

Коэффициенты полинома находятся в векторе A длины n + 1, который задается в качестве параметра функции polyroots(A)
Решение уравнения с помощью данной функции представлено на рис. 6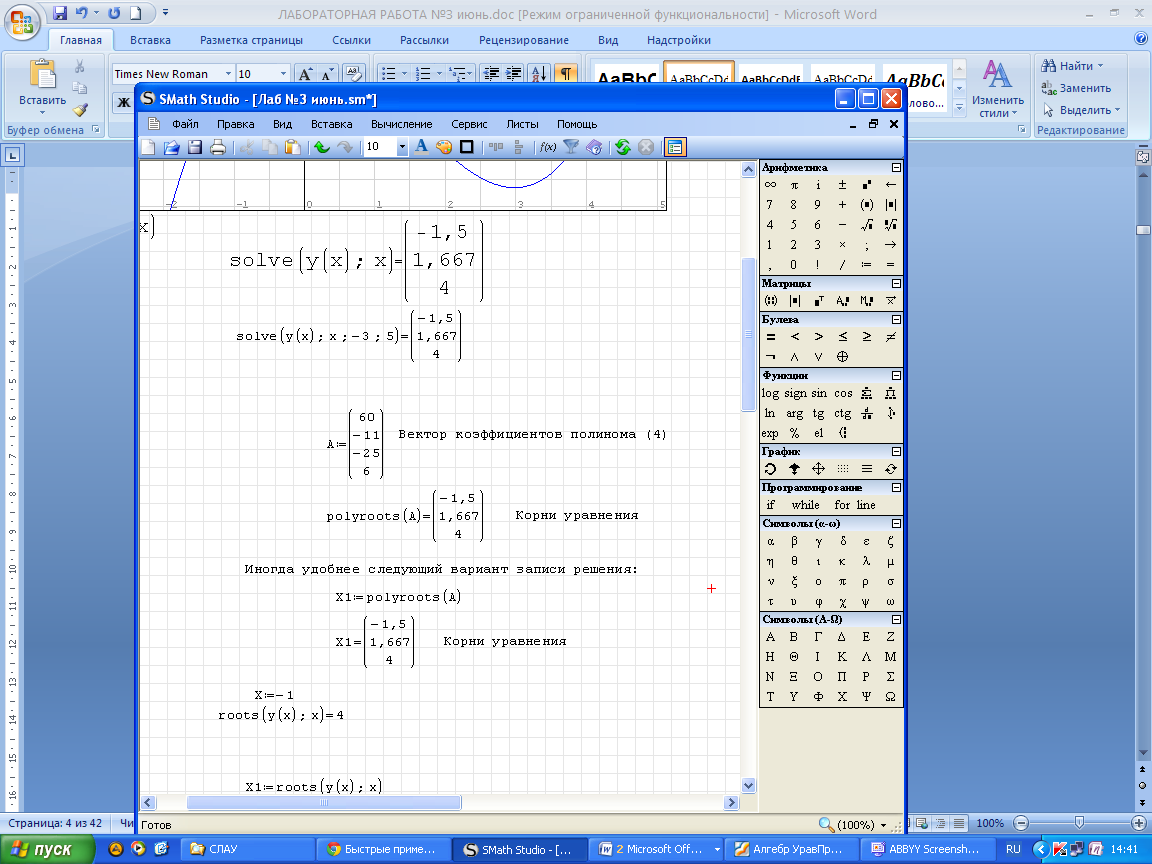


Рис. 6