ММвХТ экзамен. Метод наименьших квадратов

• Название: Метод наименьших квадратов
• Дата: 29.11.2020
• Размер: 1.77 Mb.
• Имя файла: ММвХТ экзамен.docx
• Тип: Документы; #154939
• страница: 2 из 4

Решение уравнений численными методами (solve.)

Для решения линейных и нелинейных алгебраических уравнений в SMath Studio используется функция solve, которая представлена в двух вариантах - solve(2) - возвращает действительные корни уравнения 1: выражение относительно указанной переменной 2: переменная и solve(4) – возвращает действительные корни уравнения 1: выражение внутри промежутка между 3: число и 4: число относительно указанной переменной 2:переменная
После записи данной функции на листе программы достаточно, не убирая с уравнения курсор, выполнить действие численного вычисления (кнопка "=" на клавиатуре или на панели программы). Само уравнение, записанное в качестве первого аргумента функции solve(...), может быть записано без правой части (т.е., к примеру: "x+2") или вместе с ней ("x+2=0"). Однако следует помнить, что в случае записи уравнения в полном виде (с правой частью), необходимо вместо обычного знака "=" между левой и правой частями уравнения вставлять знак булево равно (выглядит, как жирное равно).

Пример решения уравнения F(x) = 0 для обоих вариантов функции solve показан на рис. 9.

8. 
   Решение уравнений численными методами (roots).
   

В математическом пакете SMath Studio найти решение уравнения можно при помощи стандартной функции roots(2) - нахождение корней системы нелинейных уравнений. Возвращает значения 2:вектор при которых функции 1: вектор равны нулям и roots(3) – нахождение корней системы нелинейных уравнений с учетом указанных приближений 3: вектор. Возвращает значения 2: вектор при которых функции 1: вектор равны нулям
В данной функции реализован метод Ньютона для нахождения корней уравнения, поэтому необходимо задавать начальное значение x, с которого и начинается поиск корня. Чтобы решить уравнение с помощью данной функции надо выполнить следующую последовательность действий:

• 
  задать произвольное, начальное значение аргумента, неизвестной переменной решаемого уравнения;
  
• 
  сообщить вид функции f(x):=…;
  
• 
  задать функцию root по схеме root(f(x),x);
  
• 
  попросить вывести значение результата root(f(x),x)=…..
  

Примечания.

1. 
   Функция roots определяет только один корень уравнения. Если в уравнении несколько корней, то определяется тот, к которому ближе всего заданное начальное значение переменной.
   
2. 
   Функции roots можно не давать ни какого идентификатора, но поставить знак «равно» сразу после нее – компьютер сообщит значение найденного корня.
   
3. 
   Очень часто при введении функционального идентификатора f(x) в функцию roots результат не получается. В этом случае вместо идентификатора f(x) следует в функции roots напечатать вид самого уравнения, точнее его левой частиЕсли функция y(x) имеет малый наклон около искомого корня, то функция roots может сходиться к значению x, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня следует заменить уравнение y(x) = 0 на z(x) = 0:
   

z(x)=y(x)/(dy(x)/dx).

В некоторых случаях может отсутствовать сходимость функции roots. Эта ошибка может быть вызвана следующими причинами:

• 
  уравнение не имеет корней.
  
• 
  корни уравнения расположены далеко от начального приближения.
  
• 
  выражение имеет локальные экстремумы между начальным приближением и корнями.
  
• 
  выражение имеет разрывы между начальными приближениями и корнями.
  
• 
  выражение имеет комплексный корень, но начальное приближение было вещественным.
  

Чтобы установить причину ошибки, исследуйте график y(x). Он поможет выяснить наличие корней уравнения y(x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет roots сходиться.

9. 
   Методы решения нелинейных уравнений. Метод дихотомии.
   

Одним из распространенных методов решения нелинейных уравнений используется метод дихотомии (метод деления отрезка пополам). Идея метода заключается в следующем.

Пусть интервал, на котором ищется решение, равен [a, b]. Найдем середину отрезка [a, b]: c=(a+b)/2. Корень остался на одной из частей: [a, c] или [c, b]. Если f(a) * f(с)<0,токорень попал на отрезок [a, c], тогда деление отрезка можно повторить, приняв в качестве нового правого конца точку c, т.е. b=c. В противном случае корень попал на половину [c, b], и необходимо изменить значение левого конца отрезка: a=c. Поскольку корень всегда заключен внутри отрезка, итерационный процесс можно останавливать, если длина отрезка станет меньше заданной точности: |b – a|<ε .




Пример решения уравнения методом дихотомии представлен на рис. 1. Определяется искомое уравнение f(x), точность решения ε и интервал, на котором ищется решение. По окончании вычислений выводится корень уравнения, достигнутая точность и количество итераций, за которое был получен ответ.

Рис. 1

10. 
    Методы решения нелинейных уравнений. Метод хорд.
    

Для решения нелинейных алгебраических уравнений применяется также метод хорд. В этом методе кривая f(x) заменяется прямой линией – хордой, стягивающей точки (a, f(a)) и (b, f(b)). В зависимости от знака выражения f(a) f ^//(a) метод хорд имеет два варианта, изображенных на рис. 2 а, б. (Обычно знак второй производной наглядно отражает "вид" кривизны: вогнутость (f''>0 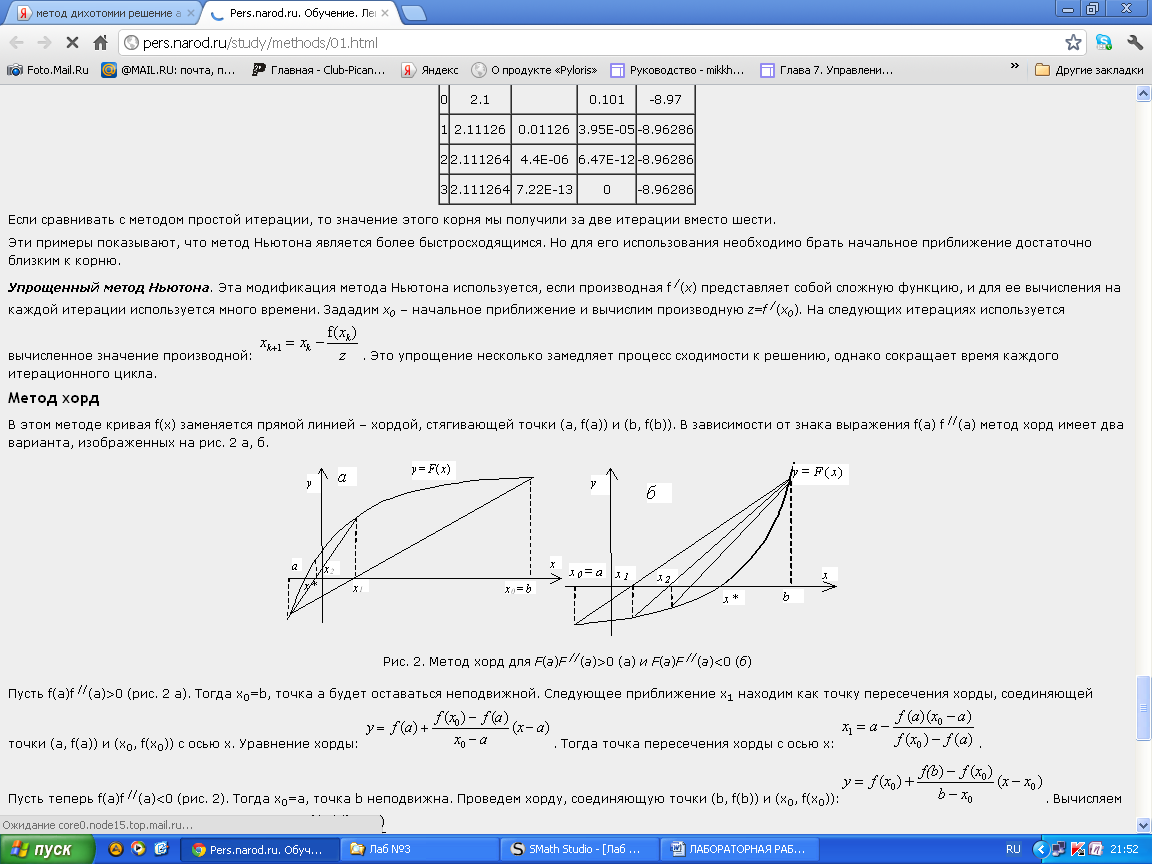) или выпуклость (f''<0 )."Изгиб губ" описывает вид кривой в окрестности точки. )

Рис. 2
Пусть f(a)f ^//(a)>0 (рис. 2 а). Тогда x₀=b, точка a будет оставаться неподвижной. Следующее приближение x₁ находим как точку пересечения хорды, соединяющей точки (a, f(a)) и (x₀, f(x₀)) с осью x. Уравнение хорды:  . Тогда точка пересечения хорды с осью x:

  .

Пусть теперь f(a)f ^//(a)<0 (рис. 2). Тогда x₀=a, точка b неподвижна. Проведем хорду, соединяющую точки (b, f(b)) и (x₀, f(x₀)): . Вычисляем точку пересечения хорды с осью x:  .

На следующей итерации в качестве x₀ надо взять вычисленное значение x₁.Таким образом, имеем следующую последовательность вычислений.



Рис. 3
Если f(a) f ^//(a)>0, то x₀=b и  .

Если же f(a) f ^//(a)<0, то x₀=a и  .

Окончание итерационного цикла в этом методе происходит по условию малости невязки уравнения: |f(x₁)| < ε или  .

Пример использования метода хорд для решения уравнения представлен на рис. 3. Пользователь определяет искомое уравнение, точность решения и интервал, на котором ищется решение.

По окончании вычислений выводится корень уравнения, достигнутая точность и количество итераций, за которое был получен ответ.

11. Решение систем линейных алгебраических уравнений матричным методом.

В некоторых химических задачах требуется решение систем линейных уравнений (СЛУ), например, анализ смесей, расчет равновесий многокомпонентных систем, сглаживание кривых, нелинейный регрессионный анализ.

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn: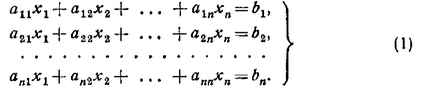



В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде :

Ах = b, (2)

где: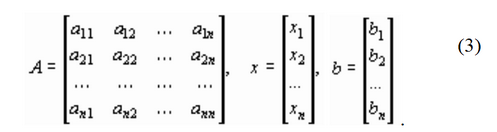



Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы; матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец х, элементы которой - искомые неизвестные, называется решением системы.

Если матрица А - неособенная, то есть det A не равен 0 то система (1), или эквивалентное ей матричное уравнение (2), имеет единственное решение. Представленные таким образом системы можно решить как аналитически, так и численно.

Умножая обе части уравнения (2) на обратную матрицу А-1,

A-1Ax=A-1b

Получим аналитическое решение системы линейных уравнений в матричном виде:

x=A-1b.(4)

Формула (4) дает решение уравнения (2) и оно единственно. Решение системы линейных уравнений в матричном виде в SMath Studio показано на рис.
12. Постановка задачи численного метода решения дифференциальных уравнений.

Дано обыкновенное дифференциальное уравнение первого порядка

у' = f (х, у). (1)

Тре6уется найти решение y=y(х) этого уравнения, удовлетворяющее начальному условию

у(х0) == y0 .(2)

Такая задача называется задачей Коши. Геометрический смысл ее решения состоит в нахождении интегральной кривой у=у(х), проходящей через заданную точку А0 (х0,у0) (рис. 1).

Существуют следующие постановки задачи Коши:

* дифференциальное уравнение первого порядка, разрешённое относительно производной: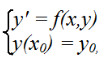



* система n дифференциальных уравнений первого порядка, разрешённая относительно производных (нормальная система n-го порядка):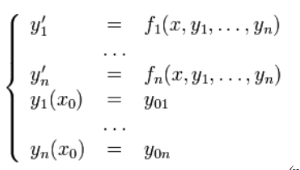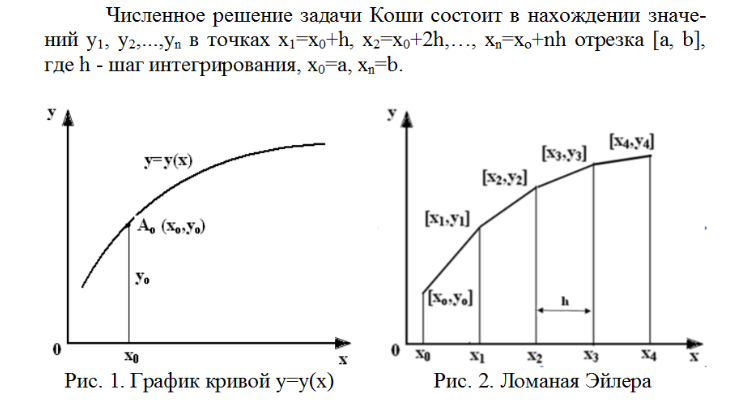







13. Метод Эйлера. Метод Рунге-Кутты

Нанеся точки (хо,уо), (х1,у1),...,(хn,уn) на координатную плоскость и соединив отрезками прямой, получим ломаную линию, называемую ломаной Эйлера, - приближенное изображение интегральной кривой (рис.2).

Самый простой и менее точный - метод Эйлера (метод первого порядка точности, расчетные формулы (4)). Наиболее распространенным является метод Рунге-Кутта (метод четвертого порядка точности, расчетные формулы (5)).

Последовательность вычислений по указанным методам следующая:



Для выполнения вычислений по методу Рунге-Кутта вручную удобно пользоваться схемой, приведенной в табл. 33. Ориентировочную оценку погрешности метода Рунге-Кутта ε можно вычислить по формуле (6)



Метод Рунге-Кутта является одним из методов повышенной точности и, несмотря на свою трудоемкость, широко используется при численном решении, как дифференциальных уравнений, так и систем дифференциальных уравнений.

Среди встроенных функций SMath Studio для численного решения дифференциальных уравнений есть встроенная функция, реализующая метод Рунге – Кутта с постоянным фиксированным шагом. Она имеет вид: rkfixed( v,x0,xk,n,F). Здесь v - начальные условия, записанные в виде вектора, x0, xk – начальное и конечное значения аргумента, n- число шагов, F- правые части системы, записанные в виде вектора. Длина шага интегрирования определяется выражением h=(xk-x0)/n.

Как и большинство методов численного решения дифференциальных уравнений, метод Рунге – Кутта требует предварительного представления дифференциального уравнения n-го порядка в виде системы дифференциальных уравнений первого порядка: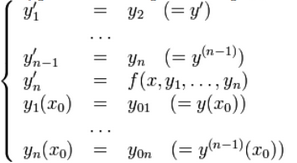



Преобразование дифференциального уравнения в систему уравнений будет рассмотрен при решении примеров.

Отметим, что в последних версиях MathCad появилась функция odesolve(х, b) (ordinary differential equation solution – решение обыкновенного дифференциального уравнения), позволяющая решать уравнение без его преобразования. Здесь х – переменная интегрирования, b- верхняя граница изменения аргумента. Нижняя граница равна нулю.

14. Решение обыкновенных дифференциальных уравнений с помощью функции rkfixed.

Встроенная функция rkfixed (метод Рунге – Кутта с фиксированным шагом решения) позволяет решать только обыкновенные дифференциальные уравнения (ОДУ) первого порядка или системы таких уравнений. Уравнения порядка выше первого требуется преобразовывать в систему уравнений первого порядка.

Задача Коши для ОДУ n–го порядка ставится следующим образом: найти решение уравнения при заданных начальных условиях: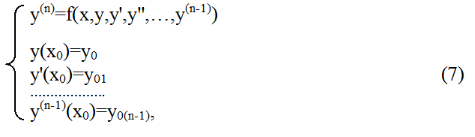



здесь y^(m) - производная m порядка от решения, m=1,2,…,n .

Основной прием, используемый при решении задач типа (7), заключается во введении новых переменных и сведении задачи решения ОДУ высокого порядка к решению системы уравнений первого порядка. Введем новые переменные

y1=y

y2=y'

…………

yn=y^(n-1)

тогда задачу (7) можно представить в виде системы n ОДУ первого порядка:



при заданных начальных условиях:



15. Построения графиков полученного решения.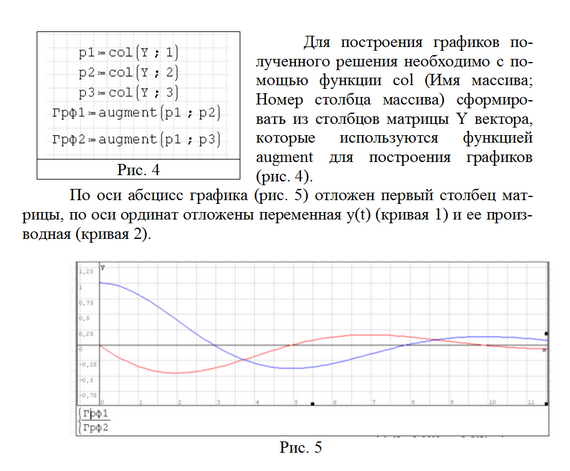



16. Меры центральной тенденции.

Существуют 3 способа выражения центральной тенденции распределения: мода, среднее арифметическое, медиана.

Мода – это наиболее часто встречающееся значение в ряду данных.

Например, в следующей выборке: {2, 3, 5, 1, 4, 5, 6, 5, 2} модой будет являться значение 5 (обозначатся следующим образом: Мо = 5). Если массив содержит 2 моды, то распределение называется бимодальным. Таким примером может служить выборка {3, 3, 5, 1, 4, 5, 6, 5, 3}. Здесь Мо1 = 5, а Мо2 = 3.

Бимодальное или полимодальное распределение могут рассматриваться как признак неоднородности выборки. Например, школьный класс образован в результате механического слияния двух разных классов, и показатели мод интеллекта были изначально различны. После слияния в объединенной выборке профиль интеллекта будет иметь 2 моды.

Среднее арифметическое – это отношение суммы всех значений данных к числу слагаемых. Среднее арифметическое обозначается как Мх или М. Число слагаемых (то есть объем выборки) обозначается буквой n.



В качестве примера можно рассмотреть последний массив: {8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20}. Мх = (8 + 9 + 11 + 2 * 12 + 13 + 14 + 17 + 2 * 19 + 2 * 20) / 12 = 14,5

Если в ряду данных присутствуют числа со знаком «минус», то суммирование производится с учетом этих знаков.

Медиана разбивает выборку на 2 равные части. Для определения медианы рекомендуется сначала упорядочить данные.

необходимо этот массив упорядочить (произвести сортировку по возрастанию): {8, 9, 11, 12, 12, 13, 15, 17, 19, 19, 20}. Медиана будет равна 13 (обозначатся след. образом: Ме = 13). Если количество данных в выборке четное, то медиана равна средней арифметической между двумя центральными значениями. {8, 9, 11, 12, 12, 13, 15, 17, 19, 19, 20, 20}, то медиана будет равна 14. В подобном случае медиана не может соответствовать ни одному из значений выборки. Медиана может принимать и дробные значения. Например, если мы в последнем примере 15 (одно из двух центральных значений) заменим на 14, то выборка примет вид {8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20} и медиана будет равна 13,5.