ММвХТ экзамен. Метод наименьших квадратов
 Скачать 1.77 Mb.
|
|
25. Непараметрические методы сравнения выборок. Критерий U-Манна-Уитни. К методам сравнения выборок, в соответствии с принятой классификацией, мы относим способы проверки статистических гипотез о различии выборок по уровню выраженности признака, измеренного в количественной шкале. Непараметрические методы сравнения выборок являются аналогами параметрических методов сравнения средних значений. И почти каждый параметрический метод сравнения средних может быть при необходимости заменен своим непараметрическим аналогом либо сочетанием непараметрических методов. Непараметрические методы заметно проще в вычислительном отношении, чем их параметрические аналоги. До недавнего прошлого простота вычислений имела существенное значение при обработке данных «вручную». Но, во-первых, данные очень часто включают одинаковые значения, усложняющие расчеты, во-вторых, компьютерная обработка снимает проблему сложности вычислений. Поэтому при выборе между параметрическими и непараметрическими методами следует исходить из свойств самих данных. Непараметрические аналоги параметрических методов сравнения выборок применяются в случаях, когда не выполняются основные предположения, лежащие в основе параметрических методов сравнения средних значений. При решении вопроса о выборе параметрического или непараметрического метода сравнения необходимо иметь в виду, что параметрические методы обладают заведомо большей чувствительностью, чем их непараметрические аналоги. Поэтому исходной ситуацией является выбор параметрического метода. И решение о применении непараметрического метода становится оправданным, если не выполняются исходные предположения, лежащие в основе применения параметрического метода. Условия, когда применение непараметрических методов является оправданным: * есть основания считать, что распределение значений признака в генеральной совокупности не соответствует нормальному закону; * есть сомнения в нормальности распределения признака в генеральной совокупности, но выборка слишком мала, чтобы по выборочному распределению судить о распределении в генеральной совокупности; * не выполняется требование гомогенности дисперсии при сравнении средних значений для независимых выборок. На практике преимущество непараметрических методов наиболее заметно, когда в данных имеются выбросы (экстремально большие или малые значения). Если размер выборки очень велик (больше 100), то непараметрические методы сравнения использовать нецелесообразно, даже если не выполняются некоторые исходные предположения применения параметрических методов. С другой стороны, если объемы сравниваемых выборок очень малы (10 и меньше), то результаты применения непараметрических методов можно рассматривать лишь как предварительные. Структура исходных данных и интерпретация результатов применения для параметрических методов и их непараметрических аналогов являются идентичными. При сравнении выборок с использованием непараметрических критериев, как и в случае параметрических критериев, обычно проверяются ненаправленные статистические гипотезы. Основная (нулевая) статистическая гипотеза при этом содержит утверждение об идентичности генеральных совокупностей (из которых извлечены выборки) по уровню выраженности изучаемого признака. Соответственно, при ее отклонении допустимо принятие двусторонней альтернативы о конкретном направлении различий в соответствии с выборочными данными. Для принятия статистического решения в таких случаях применяются двусторонние критерии и, соответственно, критические значения для проверки ненаправленных альтернатив. Перед знакомством с непараметрическими методами сравнения читателю необходимо ознакомиться с порядком и условиями применения их параметрических аналогов. При выборе того или иного непараметрического метода сравнения выборок можно руководствоваться таблицей классификации методов сравнения (см. рис. 1). Критерий U-Манна-Уитни. Формально, критерий U — это общее число тех случаев, в которых значения одной группы превосходят значения другой группы, при попарном сравнении значений первой и второй групп. Соответственно, вычисляются два значения критерия: Ux и Uy. Для вычислений «вручную» используются следующие формулы: 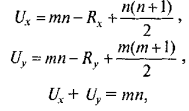 где n — объем выборки X; m — объем выборки Y, Rx и Ry — суммы рангов для X и Y в объединенном ряду. В качестве эмпирического значения критерия берется наименьшее из Ux и Uy. Чем больше различия, тем меньше эмпирическое значение U. Поскольку критерий U отражает степень совпадения (перекрещивания) двух рядов значений, то значение р-уровня тем меньше, чем меньше значение U. При расчетах «вручную» используют таблицы критических значений критерия U-Манна-Уитни (приложение 9).  Проверим гипотезу о различии выборок X (численностью т = 8) и Y (численностью п = 8) на уровне α = 0,05: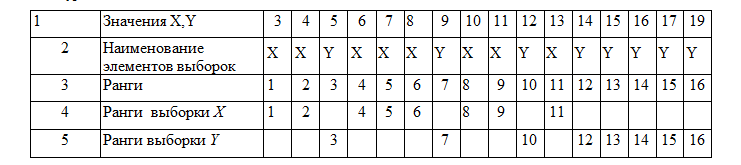 Шаг 1. Значения двух выборок объединяются в один ряд, упорядоченный в порядке возрастания или убывания (строка 1). Обозначается принадлежность каждого значения к той и другой выборке (строка 2). Шаг 2. Значения выборок ранжируются (строка 2) и выписываются отдельно ранги для одной и другой выборки (строки 4,5). Шаг 3. Вычисляются суммы рангов RX по X и Ry по Y: Rx = 46; Ry = 90. Шаг 4. Вычисляются Ux и Uy no формуле 12.1:  Шаг 5. Определяется р-уровень значимости: наименьшее из U сравнивается с табличным (приложение 9) для соответствующих объемов выборки т = 8 и п = 8. Значение р < 0,05 (0,01), если вычисленное (Uэмп ≤ Uта6л. В нашем случае наименьшим является Uy = 10, которое и принимается за эмпирическое значение критерия. Оно меньше критического для р = 0,05 (U= 13), но больше критического для р = 0,01 (U = 7). Следовательно, р < 0,05.  Шаг 6. Принимается статистическое решение и формулируется содержательный вывод. На уровне α = 0,05 принимается статистическая гипотеза о различии Х и Y по уровню выраженности признака. Уровень Y статистически достоверно выше уровня Х (р < 0,05).Замечание. Связи в рангах для вычислений «вручную» не предусмотрены. Хотя они и незначительно влияют на результат, но если доля одинаковых рангов по одной из переменных велика, то предлагаемый алгоритм неприменим, пользуйтесь компьютерной программой (SPSS, Statistica). 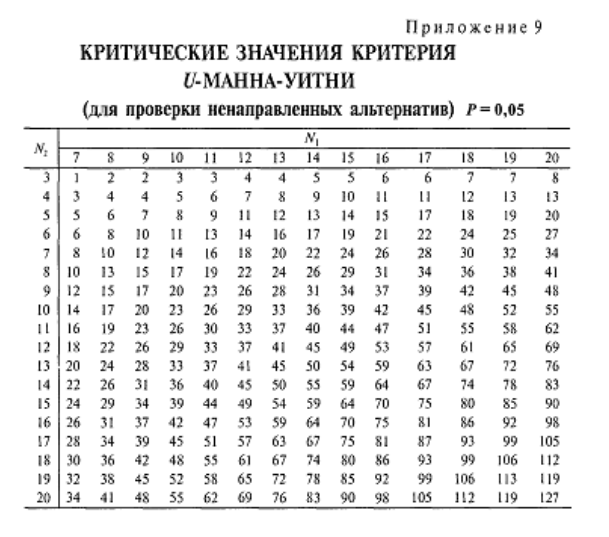 26. Задачи кластерного анализа. Кластерный анализ выполняет следующие основные задачи: · Исследование схем группировки объектов; · Выработка гипотез на базе исследований данных; · Подтверждение гипотез и исследований данных; · Определение присутствия групп внутри данных. 27. Этапы кластерного анализа. Несмотря на многообразие задач, типов данных и применяемых методов кластеризации, все исследования с применением кластерного анализа содержат пять основных этапов: 1. определение объема выборки для кластеризации; 2. определение информативных признаков, по которым будут сравниваться объекты в выборке; 3. вычисление значений меры сходства между объектами; 4. применение метода кластерного анализа для формирования групп сходных объектов; 5. проверка достоверности результатов кластерного анализа. 28. Определение информативных признаков. Определение информативных признаков, в пространстве которых будет осуществляться кластеризация, является одним из наиболее важных и ответственных шагов. Основная проблема состоит в том, чтобы найти такую совокупность признаков, которая наилучшим образом отражала бы понятие сходства. При этом количество информативных признаков не должно превышать 5 – 6, в противном случае будет формироваться большое количество кластеров, что существенно затрудняет анализ. Существует большое количество методов поиска информативных признаков, хотя они и не формализованы. Наиболее простым является метод, основанный на отборе признаков с малой корреляционной зависимостью и гистограммами, имеющими одну и более ярко выраженную моду (куполообразную форму). 29. Выбор меры сходства кластерных методов. Выбор меры сходства в большинстве случаев не является решающим фактором, хотя в некоторых задачах его правильный выбор дает существенное преимущество. Наиболее популярной матрицей в пространстве признаков является Евклидово расстояние: 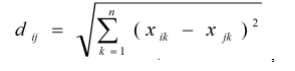 где n – размерность пространства (количество информативных признаков;  - значение k-го признака для i-го объекта.Иногда используется метрика «квадратичное Евклидово расстояние», то есть квадрат Евклидова расстояния  , чтобы придать большие веса более отдаленным друг от друга объектам.Хорошо известной мерой расстояния является «манхеттенское расстояние» или «расстояние городских кварталов», которое уменьшает влияние отдельных больших выбросов, так как они не возводятся в квадрат:  Выбор метрики обычно осуществляется экспериментальным путем для каждой конкретной задачи. 30. Нормализация признаков. Нормализация значений исходных показателей по объектам проводится потому, что исходные данные выражены обычно в разных единицах измерения и проводить между ними арифметические действия невозможно без перевода их в безразмерные единицы. Наиболее распространенный способ нормализации показателей проводится с использованием среднего квадратического отклонения по формуле: 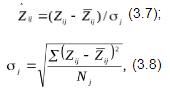 где  – нормализованная безразмерная величина; – индивидуальные значения по столбцам матрицы; – среднее значение по столбцам матрицы; – среднее квадратическое отклонение по столбцам; – объем выборки по столбцам.Составляется матрица нормализованных показателей. 31. Анализ результатов кластерного анализа(+нормализация). Применение кластерного анализа для создания групп сходных объектов (кластеров) является основным этапом решения задачи. Под кластером понимают области пространства признаков с относительно высокой плотностью точек, отделенные от других таких же областей областями с относительно низкой плотностью точек. Разработано большое количество кластерных методов, которые образуют семь основных семейств. Наиболее популярными являются методе K-средних и метод одиночных связей (семейство иерархических дивизимных (нисходящих) методов). При построении кластеров по методу одиночной связи последовательно объединяются вначале объекты наиболее близкие, а затем все более отдаленные. Вначале каждый объект рассматривается как отдельный кластер, а затем на каждом шаге работы алгоритма происходит объединение 2-х самых близких кластеров. Работа алгоритма заканчивается при получении заданного количества кластеров. Процесс построения кластеров этим методом может быть отображен в виде древовидной диаграммы – дендрограммы (иерархии кластеров) – расстояние между 1 и 2 объектами наименьшее, а между кластерами из объектов (1,2,3) и объектов (4,5,6,7) – наибольшее (рисунок 1). 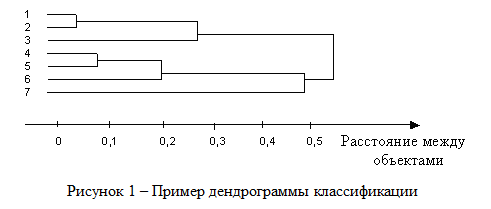 В кластеризации методом K-средних объекты перемещаются из одних групп (кластеров) в другие таким образом, чтобы получить наиболее значимый результат при проведении дисперсионного анализа (ANOVA). Результатом кластеризации является заданное количество кластеров, каждый из которых имеет свой номер и представлен перечнем объектов, включенных в соответствующие кластеры. Эта информация хранится в специально создаваемых файлах – отчетах. 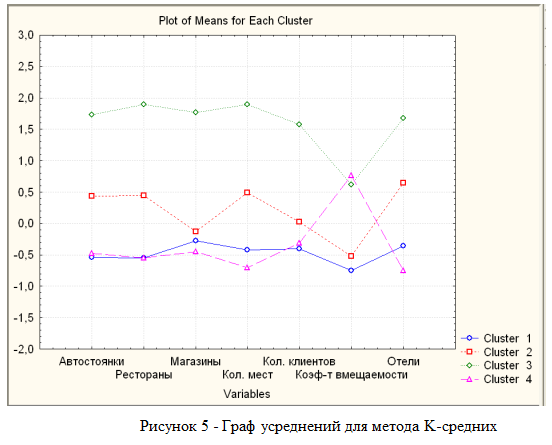 Построение кластеров в пространстве семи признаков выполнено методом K-средних. Граф усреднений (координаты центров кластеров) представлен на рисунке 5 и показывает положения центров кластеров для различных осей координат (информативных признаков). Мы выбрали 7 информативных признаков (они размещены вдоль оси абсцисс), в пространстве которых построили 4 кластера (они представлены различными условными обозначениями в легенде справа внизу). Например, кластер №1 обозначен зеленой линией, узлы которой показывают положение центра кластера №1 на конкретном параметре (колич. автостоянок=-0,5; колич. ресторанов=-0,5; кол. магазинов=-0,3; кол. мест=-0,51 и т.д. Но здесь есть одна особенность, которая заключается в том, что для исключения влияния на качество разбиения на кластеры абсолютных значений исходных признаков (например, в Крыму кол. мест=14839, кол. магазинов=18), их подвергают нормализации. Она заключается в следующем: из каждого значения в столбце таблицы вычитается математическое ожидание соответствующего столбца, а полученная разность делится на среднеквадратическое отклонение. В результате получаем для всех столбцов математическое ожидание равное нулю и среднеквадратическое отклонение равное 1. После процедуры нормализации получаем для Крыма кол. мест=1,657 и кол.магазинов=1,378, то есть числа одного порядка. На рис. 5 как раз по оси ординат отложены нормализованные значения. Отрицательные значения означают, что число меньше математического ожидания. Для возвращения к исходным значениям необходимо выполнить обратное действие: нормализованное значение умножить на среднеквадратическое отклонение и сложить полученное произведение с математическим ожиданием. На рис. 5 как раз по оси ординат отложены нормализованные значения. Отрицательные значения означают, что число меньше математического ожидания. Для возвращения к исходным значениям необходимо выполнить обратное действие: нормализованное значение умножить на среднеквадратическое отклонение и сложить полученное произведение с математическим ожиданием. |